2. 中国科学院边缘海地质重点实验室, 中国科学院南海海洋研究所, 广州 510301;
3. 中国石油东方地球物理公司物探技术研究中心, 河北涿州 072750;
4. 中国石油川庆钻探工程公司地球物理勘探公司, 成都 610200
2. Key Laboratory of Marginal Sea Geology, Chinese Academy of Sciences, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, China;
3. R & D Center of BGP, CNPC, Hebei Zhuozhou 072750, China;
4. CNPC Sichuan Petroleum Geophysical Prospecting Company 610200, China
自由表面多次波的压制已经成为海上地震资料处理的常规处理流程[1-3],而绕射多次的压制和去除则成为当今深水陡坡带和复杂海底地震资料多次波压制的重点和难点.由于绕射多次波传播路径的不确定性,时距曲线随着绕射波在自由表面反射点的不同而不同,在单炮记录上表现出较大的随机性和不确定性,从而比常规的多次波更加难以区分[4-5];目前在国内开展绕射多次波的压制和去除方法的工作还比较少,而国外已有大量研究,且大多考虑直接或者间接滤波方法[6-7];基于方位角的绕射多次波压制方法,依据绕射多次波的方位角和一次波的不同来区分和压制绕射多次波[8-10].基于小波变换的聚焦域绕射多次波压制方法[11].ADCIG域绕射多次波的消除就是间接滤波方法中较为典型的方法,考虑绕射多次波和一次波在ADCIG道集的拖尾现象,达到压制和去除绕射多次波的目的[12-14];但是在原始地震资料信噪比比较低的情况下ACDIG道集内的绕射多次波和普通多次波的差异并不明显,而且计算量大、处理压制过程特别复杂[15].
绕射多次波通常是经海底一次绕射以后导致波的传播路径发生畸变,畸变后的情况可以分为三种:第一种,畸变后波的传播方向仍然在原先设定的电缆长度的记录范围之内,经自由表面反射产生的多次波;第二种,畸变后波的传播方向超出了原先设定的电缆长度的记录范围,但是仍然由自由表面反射产生的多次波;第三种,无论是否超出了预先设定的电缆长度的记录范围,畸变后波的传播方向发生变化,在海底地层发生多次反射形成层间绕射多次波;第一种情况下的绕射多次波可以归纳到传统的SRME预测和消除多次波方法当中予以压制;第三种情况因为属于层间绕射多次波,不在本文方法的讨论范围之列;但是对于第二种情况,常规SRME方法由于电缆长度的限制,在深水陡坡带和海底构造异常复杂的情况下局限性尤为明显,绕射多次波的压制也愈加困难.本文借助炮点、检波点互换原理,将邻炮的炮记录依照互换原理引入到反馈迭代循环当中,补充绕射多次波的近偏移距信息不足和负偏移距信息缺失等问题,修正深水陡坡带因为电缆长度限制而造成的信息缺失,最大限度地准确预测深水陡坡带的与自由表面有关的绕射多次波,也可以给类似多次波偏移成像方法[16-17]提供准确可靠的绕射多次波.经过Sigsbee2b模型资料和实际资料测试,达到改善深水陡坡带的自由表面相关绕射多次波压制的目地.
2 基于反馈迭代模型的绕射多次波的压制方法在2D情况下,从波动方程出发可以推导出Kirchhoff积分,由Kirchhoff积分可以推导出Rayleigh积分,这里由第二型Rayleigh积分可以知道地震波的传播过程对应空间褶积模型的具体表达式如下[18-19]:
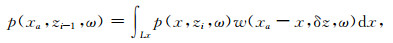
|
(1) |
式中,p(x,zi,ω)表示大地滤波器对震源的相应,w(x,δz,ω)是地层某一深度处的脉冲响应,将该公式离散后,可以得到地震波从炮点到检波点的正向传播公式:
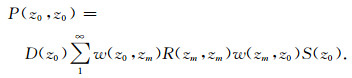
|
(2) |
由(2)式可知,地震波的传播过程可以看作是一个大地滤波过程,表示的是地震信号在地层中的传播和反射效应.由反馈迭代模型[20]可以得到2D情况下自由表面多次波的预测公式:
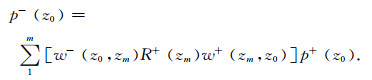
|
(3) |
上式的物理解释可以用图 1说明.
|
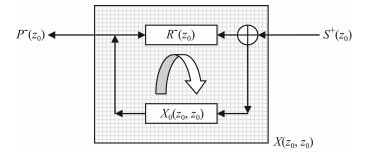
图 1 自由表面多次波的反馈迭代模型 Fig. 1 Feedback iteration model of free surface related multiple |
在z0界面激发的源波场S+(z0)向下传播经过大地滤波器X0(Z0,Z0)滤波后,返回Z0界面为上行波场P-(Z0),再经接收仪器D(Z0)的滤波后得到只有一次反射波的波场记录P(Z0),而由于Z0界面向下反射R-(Z0)作用,使得大地滤波器X0(Z0,Z0)变为带有反馈的大地滤波器X(Z0,Z0),经过反馈大地滤波器X(Z0,Z0)得到的波场记录P(Z0)就是含有表面多次波的地震记录.
联合(2)式和(3)式有:
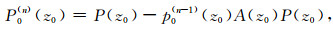
|
(4) |
在频率域将(4)式进一步简化有:
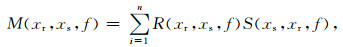
|
(5) |
其中,
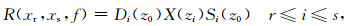
|
(6) |
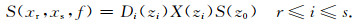
|
(7) |
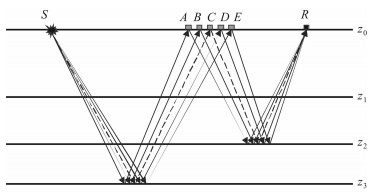
式中,xr、xs为震源和检波器位置坐标,S(xr,xs,f)表示共炮点道集,(6)式中Si(Z0)表示不同的炮对应大地检波器在不同的检波器上的响应,R(xr,xs,f)表示共检波点道集,(7)式中S(Z0)表示当前炮对应大地滤波器在不同检波器上的响应;该式的物理意义可以理解为在当前观测系统下,频率域的共炮点道集和共检波点道集相乘相加或者时间空间与的褶积,物理意义如图 2所示.
|
图 2 2D情况下自由表面多次波的示意图 Fig. 2 2D free surface related multiple prediction sketch map |
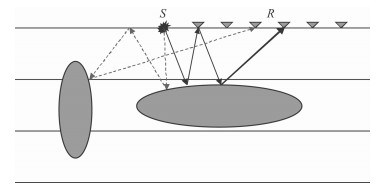
与自由表面相关的绕射多次波遵循多次波传播的一般规律,由于单边海上拖缆数据采集的拖缆长度限制,在复杂海底地质构造情况下,炮记录上记录到的绕射多次波常常超出xs、xr范围(即最大/最小偏移据范围之外)(如图 3所示虚线),依照传统的SRME方法已经不能很好的解决复杂海底的绕射多次问题.
|
图 3 与自由表面相关绕射多次波示意图 Fig. 3 Free surface related diffracted multiple sketch map |
针对绕射多次波的产生机理,在现有单边海上数据采集基础上,通过将邻炮的炮记录依照炮、检互换原理引入到反馈迭代循环当中(如图 3中虚线部分地震记录信息),补充绕射多次波的近偏移距信息不足和负偏移距缺失,则对公式(6)、(7)做如下改进;
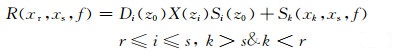
|
(8) |
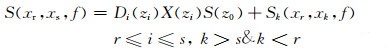
|
(9) |
其中,Sk(xk,xs,f),Sk(xr,xk,f)分别是将邻炮的炮记录通过炮检互换原理补充到常规反馈迭代多次波模型中的近偏移距和负偏移距信息,将(8)和(9)式代入到(5)式当中并简化,有:
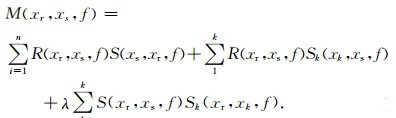
|
(10) |
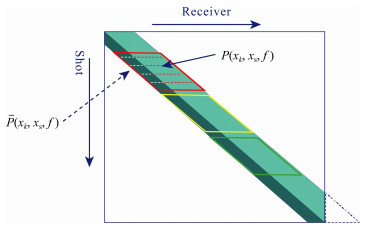
该式的物理意义可以理解为叠前炮记录上的自由表面相关多次波可以由炮点检波点之间的自由表面多次波和当前炮的最小最大偏移距之外的绕射多次波之和,λ为叠加系数因子,λ的选择需要依据实际资料而定.如图 4所示,P(xr,xs,f)为海上拖缆记录到的地震记录,P(xk,xs,f)为通过炮点检波点互换补充至P(xr,xs,f)负偏移距的部分记录信息.
|
图 4 通过将波场外推补齐负偏移距后改进的观测系统 Fig. 4 The observation system with negative offset data by wave extrapolation |
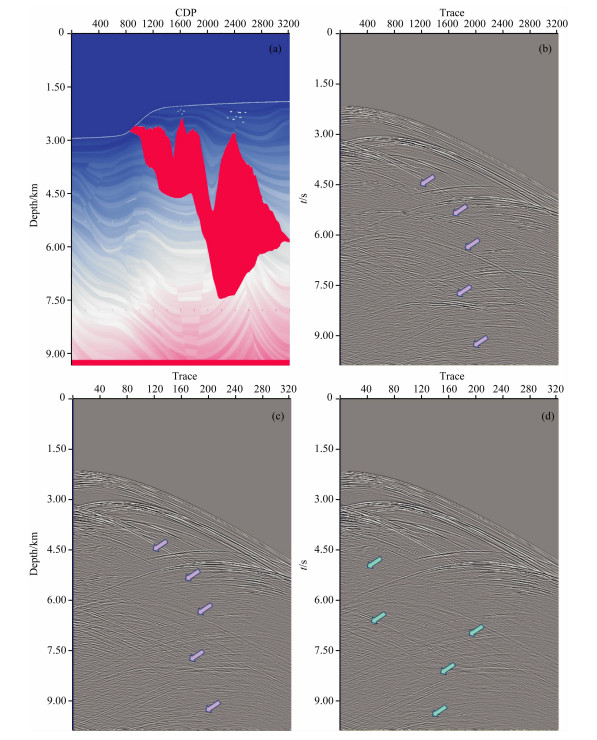
图 5a为SMARRT发布的Sigsbee2b模型,Sigsbee2b是墨西哥湾深水模型,由于该模型构造复杂、绕射点多,故而绕射多次波异常发育.该模型划分为3200×1200个网格,水平方向和垂直吹响网格间距均为7.6m.该模型的观测系统设计有500炮的正演模拟,最小检波距为0,最大炮检距约为3900m,炮距为检波距2倍,前348炮为每炮348道,往后每炮依次减少2道;
|
图 5 Sigsbee2b速度模型模拟结果 (a) Sigsbee2b速度模型;(b) Sigsbee2b速度模型的合成记录;(c)常规反馈迭代模型去除多次波后的结果;(d)改进后的绕射多次波后的结果. Fig. 5 Model simulation results of Sigsbee2b (a) Sigsbee2b velocity model; (b) The simulation record without direct wave; (c) The result of common SRME elimination multiple; (d) The result of SRME based on wave extrapolation. |
图 5b为该模型的第251炮正演记录,由该正演模型记录可以发现时距曲线为标准双曲类型的自由表面多次波相当发育,但由于盐丘和绕射点的原因,时距曲线为非双曲类型的多次波也相当发育,而且能量相当强;采用同样的均衡多道二范数匹配相减[21]以后可以得到,图 5c为仅使用传统的SRME方法消去多次波以后的记录,从该记录上不难发现双曲类型的自由表面多次波的压制和去除已经相当明显,但是近偏移距附近的非双曲类型的绕射多次波仍然存在.图 5d为经由基于波场外推的SRME绕射波消去方法以后得到的结果,不难看出近偏移距以及时距曲线为非双曲类型多次压制效果明显,有效信息得到了明显增强.
3.2 实际资料应用该数据为南海深水盆地某二维海洋地震叠加剖面,其海水深度变化大,构造复杂且陡坡带绕射多次波较为明显,常规的自由表面多次波消除方法不能较好的解决深水陡坡带的绕射多次波压制;采用改进的反馈迭代方法以后,可以更为准确地预测和匹配压制深水陡坡带绕射多次波,通过均衡多道匹配滤波以后可以得到如下所示结果,图 6a为自由表面绕射多次波压制前的叠加剖面,图 6b为自由表面绕射多次波压制后的叠加剖面,从两个椭圆标注出的范围不难发现由于陡坡带和崎岖海底产生的绕射多次波得到了较好的压制,被多次波掩盖的一次波能量得到显现.

|
图 6 实际资料处理效果对比 Fig. 6 Stacked section of original field data (a) and stacked section without diffracted multiple (b) (a)绕射多次波压制前的叠加剖面; (b)绕射多次波压制后的叠加剖面. |
深水陡坡带和复杂海底的绕射多次波受到采集拖缆的长度限制,由陡坡带和复杂海底产生的绕射多次波压制方法是海上资料处理的一个难题,本文在反馈迭代模型的基础上,依据炮点检波点互换原理,引入相邻炮记录的相关信息,补充了由于绕射而导致炮记录的近偏移距信息不足和负偏移距信息缺失问题,通过Sigsbee2b模型和实际资料的压制结果对比分析,较好地证明了该方法的有效性.另外,海上拖缆采集的方向也和自由表面绕射多次波的预测也有较大影响,采用不同方向采集的拖缆数据综合处理应该会效果更好.
| [1] | 李鹏, 刘伊克, 常旭, 等. 多次波问题的研究进展. 地球物理学进展 , 2006, 21(3): 888–897. Li P, Liu Y K, Chang X, et al. Progress on the multiple problems. Progress in Geophysics (in Chinese) , 2006, 21(3): 888-897. |
| [2] | 李鹏.复杂介质多次波处理方法研究.北京:中国科学院地质与地球物理研究所, 2007. Li P. The seismic processing method of multiple suppression of complicated medium (in Chinese). Beijing: Institute of Geology and Geophysics of CAS (Chinese Academy of Science), 2007. |
| [3] | 金德刚, 常旭, 刘伊克. 逆散射级数法预测层间多次波的算法改进及其策略. 地球物理学报 , 2008, 51(4): 1209–1217. Jin D G, Chang X, Liu Y K. Algorithm improvement and strategy of internal multiples prediction based on inverse scattering series method. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1209-1217. |
| [4] | Guitton A. Multiple attenuation in complex geology with a pattern-based approach. Geophysics , 2005, 70(4): V97-V107. DOI:10.1190/1.1997369 |
| [5] | Lu G C, Ursin B, Lutro J. Model-based removal of water-layer multiple reflections. Geophysics , 1999, 64(6): 1816-1827. DOI:10.1190/1.1444687 |
| [6] | Brittan J, Wrench A. Attenuation of multiple diffractions using a cascaded noise removal sequence. SEG Technical Program Expanded Abstracts, 2004: 1321-1324. |
| [7] | Foster D J, Mosher C C. Suppression of multiple reflections using the radon-transform. Geophysics , 1992, 57(3): 386-395. DOI:10.1190/1.1443253 |
| [8] | Barley B, Summers T. Multi-azimuth and wide-azimuth seismic: Shallow to deep water, exploration to production. The Leading Edge , 2007, 26(4): 450-458. DOI:10.1190/1.2723209 |
| [9] | Estevez R, Claerbout J F. Wide-angle diffracted multiple reflections. Geophysics , 1982, 47(9): 1255-1272. DOI:10.1190/1.1441386 |
| [10] | Widmaier M, Keggin J, Hegna S, et al. The use of multi-azimuth streamer acquisition for attenuation of diffracted multiples. SEG Technical Program Expanded Abstracts , 2002, 2002: 89-92. |
| [11] | Yu Z, Kabir N, Matson K. Diffracted multiple attenuation using wavelet filter in the focused domain. SEG Technical Program Expanded Abstracts , 2005: 2072-2075. DOI:10.1190/SEGEAB.24 |
| [12] | Alvarez G. Mapping of water-bottom and diffracted 2D multiple reflections in data space. SEP Stanford Exploration Project, 2005: 129-154. |
| [13] | Alvarez G, Biondi B, Guitton A. Attenuation of specular and diffracted 2D multiples in image space. Geophysics , 2007, 72(5): V97-V109. DOI:10.1190/1.2759439 |
| [14] | Artman B, Alvarez G, Matson K. Image-space surface-related multiple prediction. Geophysics , 2007, 72(2): S113-S122. DOI:10.1190/1.2436845 |
| [15] | Sava P, Guitton A. Multiple attenuation in the image space. Geophysics , 2005, 70(1): V10-V20. DOI:10.1190/1.1852789 |
| [16] | Liu Y K, Chang X, Jin D G, et al. Reverse time migration of multiples for subsalt imaging. Geophysics , 2011, 76(5): Wb209-Wb216. DOI:10.1190/geo2010-0312.1 |
| [17] | Berkhout A J, Verschuur D J. Imaging of multiple reflections. Geophysics , 2006, 71(4): Si209-Si220. DOI:10.1190/1.2215359 |
| [18] | Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, Part I: Theoretical considerations. Geophysics , 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [19] | Verschuur D J, Berkhout A J. Estimation of multiple scattering by iterative inversion, Part II: Practical aspects and examples. Geophysics , 1997, 62(5): 1596-1611. DOI:10.1190/1.1444262 |
| [20] | Kennett B L N. The suppression of surface multiples on seismic records. Geophysical Prospecting , 1979, 27(3): 584-600. DOI:10.1111/gpr.1979.27.issue-3 |
| [21] | 李鹏, 刘伊克, 常旭, 等. 均衡拟多道匹配滤波法在波动方程法压制多次波中的应用. 地球物理学报 , 2007, 50(6): 1844–1853. Li P, Liu Y K, Chang X, et al. Application of the equipoise pseudomulti-channel matching filter in multiple elimination using wave-equation method. Chinese J. Geophys. (in Chinese) , 2007, 50(6): 1844-1853. |
 2013, Vol. 56
2013, Vol. 56


