2. 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
3. 中石化胜利石油管理局石油开发中心, 山东东营 257000
2. School of Geoscience, China University of Petroleum (Huadong), Shandong Qingdao 266580, China;
3. Petroleum Development Center of SINOPEC Shengli Oilfield, Shandong Dongying 257000, China
目前,大多数偏移速度分析方法都是建立在各向同性声波波动理论的框架下[1-8].一般的做法是将多波多分量记录的垂直分量和水平分量分别看作纵波和转换横波进行类似于声波纵波的常规处理.然而,实际介质中的地震波是一种弹性矢量波,利用这种声波近似难以准确描述矢量波的特性,并且其处理效果在很大程度上依赖于波场分离的精度.要想获得高精度的多波多分量速度分析结果,必须在弹性矢量波的框架下进行PP波和PS波联合偏移速度分析.然而,基于弹性矢量波理论的资料处理在地震勘探中还比较薄弱,国内外相关的偏移成像[9-12]以及速度分析[13-16]研究也为数不多.
基于射线理论的走时层析是工业界应用最为广泛的速度精细化建模工具[17-18].但是,其大多数计算时间都用于进行偏移成像.弹性矢量波高斯束叠前深度偏移是一种快速、灵活以产生多波联合角道集的成像方法[19],并且与走时层析共同建立在弹性波射线理论基础上,不失为一种构建多波联合层析反演的好方法.基于以上考虑,笔者推导了多波联合层析速度反演方程以及走时残差与角道集剩余曲率的转换关系式,提出了一种利用成像域角道集更新P波、S波速度的走时层析反演方法.基于高斯束实现矢量波场成像并提取角道集,利用层析反演方程求解慢度更新量,最终获得多波联合反演结果.模型试算和实际资料处理验证了该方法的反演效果,能够为弹性矢量波联合深度偏移提供高质量的叠前速度场.
2 方法原理弹性矢量波成像域走时层析反演的主要思路是:利用弹性矢量波高斯波束叠前深度偏移提取的角度域共成像点道集(ADCIGs,简称角道集)获取走时残差,将一系列角度的射线走时残差沿着射线路径反投影得到P波和S波剩余慢度场,实现速度的更新反演.
2.1 弹性矢量波走时层析反演方程在声波走时层析成像理论的基础上推导弹性矢量波层析反演方程.首先,利用sP1和sP2分别表示扰动前、后的介质P波慢度,LP1和LP2分别表示扰动前、后的P波灵敏度矩阵,tPP1和tPP2分别表示扰动前、后的PP波射线走时,则有
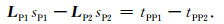
|
(1) |
假定界面位置变化引起的深度扰动不大[20],近似地有LP1=LP2=LP,则
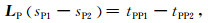
|
(2) |
即弹性矢量波中PP波走时层析反演方程可以写为:
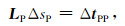
|
(3) |
式中,LP为P波灵敏度矩阵,其元素对应于网格内P波速度场的射线路径长度,ΔtPP为PP波走时残差向量,ΔsP为待反演的P波慢度更新量.
同PP波类似,利用sS1和sS2分别表示扰动前、后的介质S波慢度,LS1和LS2分别表示扰动前、后的S波灵敏度矩阵,ΔtPS表示PS波走时残差向量,则有
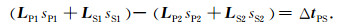
|
(4) |
同样,近似地有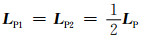
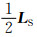
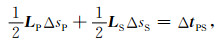
|
(5) |
将(3)式代入(5)式可得
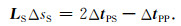
|
(6) |
(6)式即为弹性矢量波PS波走时层析成像方程,式中LS为S波灵敏度矩阵,其元素对应于网格内S波速度场的射线路径长度,ΔtPS为PS波走时残差向量,ΔsS为待反演的S波慢度更新量.
根据上述公式推导,弹性矢量波走时层析反演方程组为:
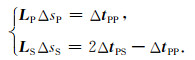
|
(7) |
因此,利用弹性矢量波成像域走时层析实现速度反演,关键在于灵敏度矩阵的确定和走时残差的求取.灵敏度矩阵是通过在纵、横波速度场中进行射线追踪获得的,其矩阵元素代表第i条射线在第j个网格内的射线路径长度.而走时残差可以通过拾取的深度残差(角道集的剩余曲率)转换得到.
2.2 弹性矢量波走时残差与深度残差的转换关系 2.2.1 PP波走时残差与深度残差的转换关系推导走时层析中,由于界面位置扰动引入的PP波深度残差ΔzPP,使射线发生改变(即由图示射线1变为射线2),这个过程中射线经过的额外路径长度lP=a1+a2,由此产生的PP波走时残差ΔtPP=lPsP.根据图 1所示几何关系,易得
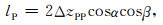
|
(8) |
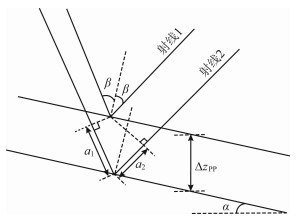
|
图 1 PP波走时残差与深度残差转换关系示意图 Fig. 1 Transformation of time residual and depth deviation for PP-wave |
则弹性矢量波中PP波走时残差和深度残差转换关系式为:
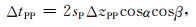
|
(9) |
式中,ΔzPP为PP波深度残差,sP为成像点处的P波慢度值,α为反射层倾角,β为入射角.
2.2.2 PS波走时残差与深度残差的转换关系推导同样,由于界面位置扰动引入的PS波深度残差ΔzPS,使射线发生改变引入的PS波走时残差ΔtPS为
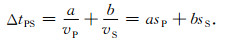
|
(10) |
根据Snell定律,即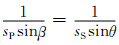
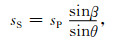
|
(11) |
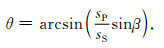
|
(12) |
将(11)式代入(10)式可得
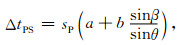
|
(13) |
根据图 2中的几何关系可得
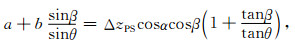
|
(14) |
|
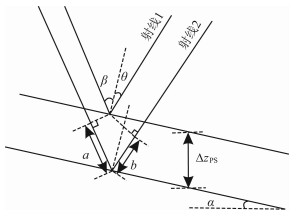
图 2 PS波走时残差与深度残差转换关系示意图 Fig. 2 Transformation of time residual and depth deviation for PS-wave |
将(14)式代入(13)式,可得
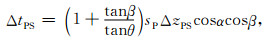
|
(15) |
式中,ΔzPS为PS波深度残差,β为(P波或S波)入射角,θ为S波反射角.
2.3 高斯波束成像角道集偏移张角与P波、S波反射角的关系在进行PP波成像时,P波反射角等同于声波情况下的反射角,在此不再赘述.
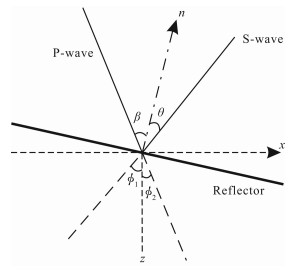
在进行PS转换波成像时,P波和S波反射角可以通过以下方式进行求解.如图 3,假设角度沿参考轴的顺时针方向为正,则在地下共成像点处P波和S波高斯波束同正z轴方向的夹角分别为Φ2和Φ1,n为反射界面法线,待求的P波和S波反射角分别为β和θ.
|
图 3 成像角道集偏移张角与P波、S波反射角的关系 Fig. 3 Relationship between open angle of ADCIGs and reflective angle for P-and S-wave |
由图 3中的几何关系可以得到
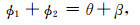
|
(16) |
根据Snell定律,
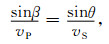
|
(17) |
将式(16)代入式(17),可得
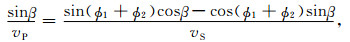
|
(18) |
将(18)式进行化简,可得
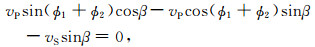
|
(19) |
求解该方程可得到P波反射角β为:
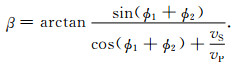
|
(20) |
同理可以求得S波反射角θ为:
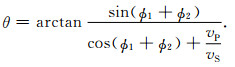
|
(21) |
在求得P波和S波反射角以后,便可以直接进行弹性矢量波高斯波束角道集的提取.
2.4 弹性矢量波成像域走时层析反演的实现为了解决层析方程的严重病态性,提高反演的稳定性,本文采用加入一阶导数型正则化(对应于“最平坦解”的思想)的LSQR方法求解层析方程组.将正则化矩阵Γ补在原灵敏度矩阵的下方,Γ由横向一阶导数型正则化矩阵Γh和纵向一阶导数型正则化矩阵Γv两部分组成[21].以一个m×n个网格的区域为例,计算时选取矩阵的行为快维,则其横向一阶导数型正则化矩阵Γh为

|
纵向一阶导数型正则化矩阵Γv为
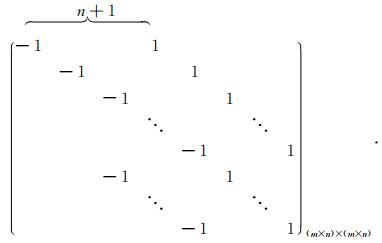
|
综上所述,弹性矢量波成像域走时层析反演的实现步骤可以概括为:
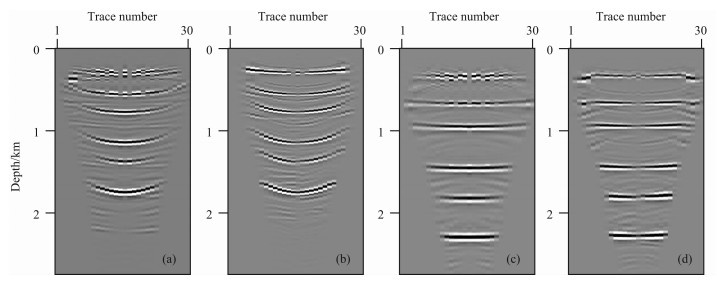
(1) 输入原始叠前多分量地震数据,通过纵波叠加速度分析、转换波叠加速度分析得到初始的纵波及转换波均方根速度场,根据复合速度的概念利用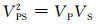
(2) 在初始纵波、横波层速度场中进行射线追踪求取P波、S波灵敏度矩阵;
(3) 利用初始纵波、横波层速度场对多分量地震数据进行弹性矢量波高斯波束叠前深度偏移,获取PP波、PS波成像结果及相应的角道集,并根据走时残差与深度残差的转换关系求取PP波和PS波走时残差向量;
(4) 加入相应的正则化矩阵,建立弹性矢量波成像域走时层析反演方程组,通过求解方程组获取纵波和横波慢度更新量以更新速度;
(5) 根据PP波、PS波角道集的拉平程度、多波(纵波和转换波)成像深度一致性原则以及层析反演的精度要求确定是否需要迭代,若需迭代则保持上覆层位速度与深度不变,返回步骤2继续进行层析更新,否则反演结束,终止迭代;
(6) 误差和灵敏度分析.
该方法在反演迭代的过程中每一层至多需要3~4次迭代就可以得到较好的反演效果,计算时间主要消耗在叠前深度偏移及角道集抽取过程中,利用基于CPU或者GPU的并行计算(本研究采用基于CPU平台的并行运算)可以提高计算效率.
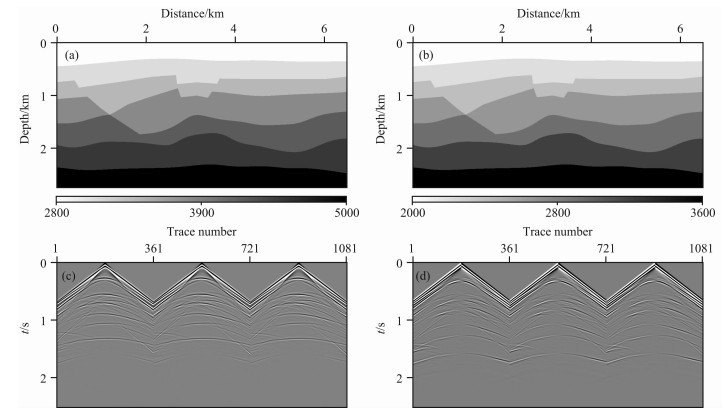
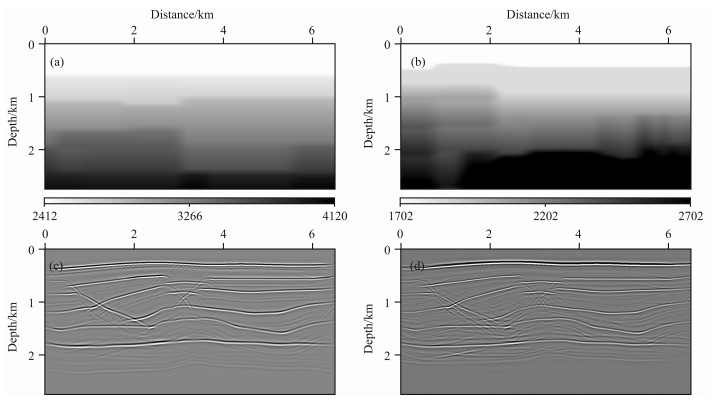
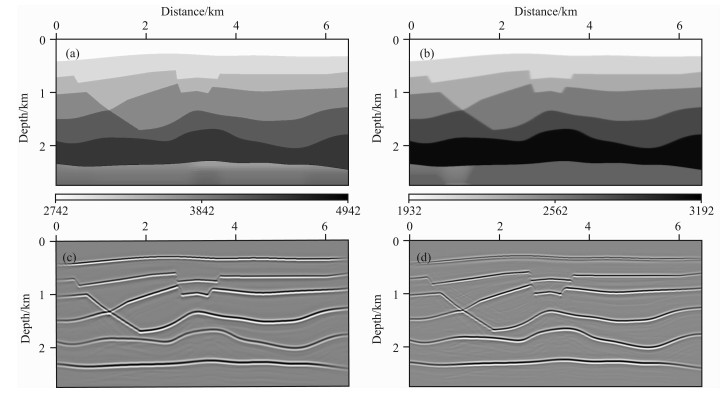
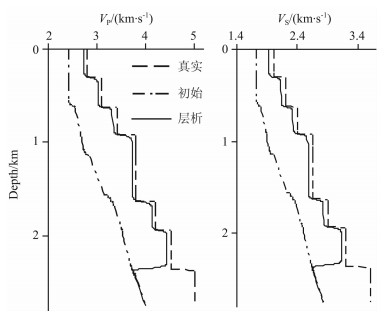
3 模型试算以下是某探区典型地震地质模型的多波层析反演结果.该模型(图 4a-4b)的网格大小是650× 550,纵横向采样间隔分别为5m和10m.多波数据(图 4c-4d)共有200炮,每炮361道接收,采样间隔2.1ms.角道集角度范围为-30°到30°,角度间隔为1°.本研究将密度设置为常数.首先,利用常规速度分析方法获取P波和PS波初始速度,估算横波初始速度,得到初始的纵、横波速度场(图 5a-5b).应用高斯束偏移获取PP、PS波初始偏移结果及角道集(图 5c-5d和图 6a-6b),由于速度不正确,初始偏移剖面上绕射波没有收敛,界面深度没有归位,角道集上同相轴上翘.走时层析后,得到了较好的偏移剖面以及拉平的角道集(图 7c-7d和图 6c-6d),PP、PS波的成像深度一致,更新后的速度场展示在图 7a-7b中.对比P波、S波初始速度、层析速度与真实速度(图 8),可以得到结论:除了缺乏角道集信息的最底层以外,其它各层的层析速度与真实速度吻合度较好,并且反演得到的P波速度可靠性要高于S波.这主要是由矢量波层析反演与偏移成像之间的制约关系决定的,PP波成像仅与P波速度有关,而PS波成像与P波、S波速度均有关系,因此无论偏移成像还是速度反演,PP波精度都稍好于PS波.
|
图 4 地震地质模型速度场及多分量叠前数据 (a) P波速度场;(b) S波速度场;(c)Z分量炮记录;(d)X分量炮记录. Fig. 4 Seismic-geologic velocity model and multi-component prestack data (a) P-wavevelocity; (b) S-wavevelocity; (c) Z-componentrecord; (d) X-componentrecord. |
|
图 5 模型初始速度场及相应的叠前深度偏移剖面 (a) P波速度场;(b) S波速度场;(c) PP波偏移结果;(d) PS波偏移结果. Fig. 5 Initial velocity field and image of prestack depth migration for the model (a) P-wavevelocity; (b) S-wavevelocity; (c) PP-waveimage; (d) PS-waveimage. |
|
图 6 模型PP波和PS波初始角道集和层析角道集 初始角道集:(a) PP波;(b) PS波.层析角道集:(c) PP波;(d) PS波. Fig. 6 Initial ADCIGs and tomography ADCIGs of PP-and PS-wave for the model Initial ADCIGs:(a) PP-wave; (b) PS-wave. Tomography ADCIGs:(a) PP-wave; (b) PS-wave. |
|
图 7 模型层析速度场及相应的叠前深度偏移剖面 (a) P波速度场;(b) S波速度场;(c) PP波偏移结果;(d) PS波偏移结果. Fig. 7 Tomography velocity field and image of prestack depth migration for the model (a) P-wavevelocity; (b) S-wavevelocity; (c) PP-waveimage; (d) PS-waveimage. |
|
图 8 模型Distance=1.25km处P波、S波真实速度、初始速度和层析速度对比 Fig. 8 Comparison of true, initial and tomography velocity in location of 1.25km for the model |
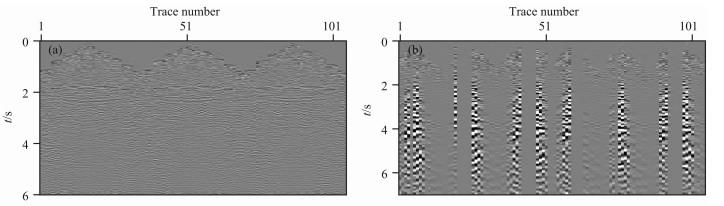
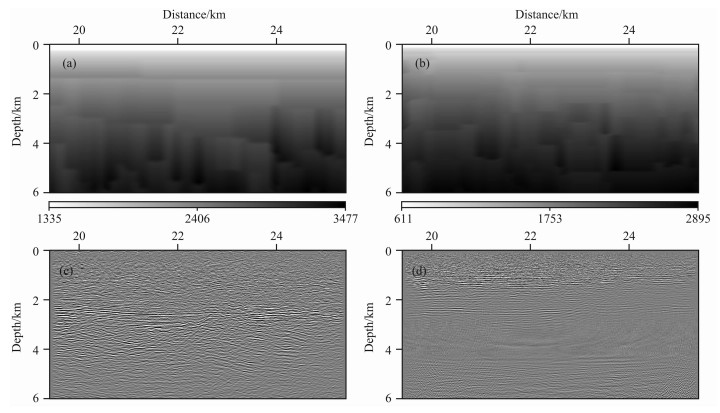
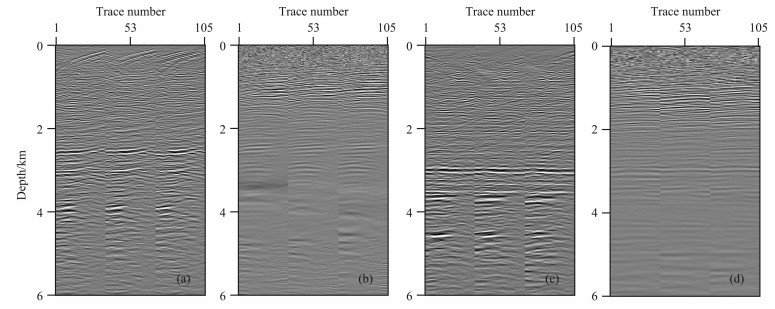
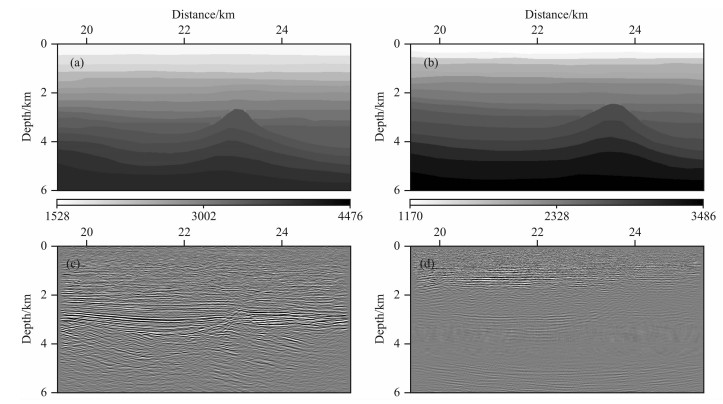
图 9是中国东部某探区实际多波多分量数据的联合层析反演结果.该数据的Z、X分量记录长度分别为6s和7s,采样间隔4 ms,道间距12m,最大偏移距2700m,覆盖的CDP范围为1901~2901.由图 9可以看到X分量数据缺道较多,信噪比不高,Z分量资料品质明显好于X分量.角道集角度范围为0°~34°,角度间隔为1°.将密度设置为常数.首先,利用常规速度分析方法获取P波和PS波初始速度,估算横波初始速度,得到初始的纵、横波速度场(图 10a-10b).应用高斯束偏移获取PP、PS波初始偏移结果及角道集(图 10c-10d,图 11a-11b),由于速度不正确,偏移剖面上浅层噪音干扰严重,PP、PS波角道集同相轴上翘.走时层析后,得到了较好的偏移剖面以及拉平的角道集(图 12c-12d,图 11c-11d),PP、PS波的成像深度基本一致,更新后的速度场展示在图 12a-12b中.对比图 12a和图 12b可以看出:PP波成像剖面明显好于PS波,究其原因,其一是由于原始数据Z分量资料品质好,信噪比高,而X分量数据缺失严重,其二是因为PP波成像仅与P波速度有关,而PS波成像与P波、S波速度均有关系.在该实际资料处理过程中,没有经过数据的叠前预处理,由于受成像角道集分辨率的影响,低信噪比的多分量数据会对层析反演产生较大影响,因此若对资料进行精细的配套预处理,有望得到令人满意的多波联合偏移和反演结果.
|
图 9 多分量叠前实际数据 (a)Z分量炮记录;(b)X分量炮记录. Fig. 9 Prestack multi-component real data (a) Z-component; (b) X-component. |
|
图 10 多分量数据初始速度及叠前深度偏移结果 (a) P波速度;(b) S波速度;(c) PP波偏移结果;(d) PS波偏移结果. Fig. 10 Initial velocity and image of prestack depth migration for multi-component data (a) P-wavevelocity; (b) S-wavevelocity; (c) PP-waveimage; (d) PS-waveimage. |
|
图 11 多分量数据初始角道集和层析角道集 初始角道集:(a) PP波;(b) PS波.层析角道集:(c) PP波;(d) PS波. Fig. 11 Initial ADCIGs and tomography ADCIGs for PP-and PS-wave for multi-component data |
|
图 12 多分量数据层析速度及叠前深度偏移结果 (a) P波速度场;(b) S波速度场;(c) PP波偏移结果;(d) PS波偏移结果. Fig. 12 Tomography velocity and image of prestack depth migration for multi-component data (a) P-wavevelocity; (b) S-wavevelocity; (c) PP-waveimage; (d) PS-waveimage. |
本文基于地震弹性矢量波场框架,推导了多波联合层析速度反演方程以及走时残差与角道集剩余曲率的转换关系式,提出了一种利用成像域角道集更新P波、S波速度的联合走时层析反演方法.建立在弹性矢量波场理论基础上的层析反演,同实际地下介质传播规律较为吻合,能够充分利用弹性矢量波的信息以反演地下速度信息,因此反演精度较高;成像域层析反演的计算时间主要消耗在偏移成像上,采用弹性矢量波高斯束叠前深度偏移能够提高计算效率,得到精度较高的成像结果以及角道集,利于走时层析的实现.模型试算和实际资料处理验证了该方法具有较高的多波联合速度反演精度和计算效率,能够得到质量较好的矢量波叠前偏移结果.其中,反演得到的P波速度可靠性要高于S波.但是低信噪比的叠前数据会对层析反演产生较大影响,因此需要做好多波数据的叠前预处理工作以保证算法精度.
| [1] | Stolk C C, Symes W W. Kinematic artifacts in prestack depth migration. Geophysics , 2004, 69(2): 562-575. DOI:10.1190/1.1707076 |
| [2] | Prucha M L, Biondi B L, Symes W W. Angle-domain common image gathers by wave-equation migration. SEG Technical Program Expanded Abstracts , 1999, 18: 824-827. |
| [3] | Clapp R G, Biondi B. Tau domain migration velocity analysis using angle CRP gathers and geologic constraints. SEG Technical Program Expanded Abstracts , 2000, 19: 926-929. |
| [4] | Xu S, Chauris H, Lambaré G, et al. Common-angle migration: A strategy for imaging complex media. Geophysics , 2001, 66(6): 1877-1894. DOI:10.1190/1.1487131 |
| [5] | Sava P, Fomel S. Time-shift imaging condition. SEG Technical Program Expanded Abstracts , 2005, 24: 1850-1853. |
| [6] | Sava P, Fomel S. Time-shift imaging condition in seismic migration. Geophysics , 2006, 71(6): S209-S217. DOI:10.1190/1.2338824 |
| [7] | Zhang K, Li Z C, Zeng T S, et al. Residual curvature migration velocity analysis for angle domain common imaging gathers. Applied Geophysics , 2010, 7(1): 49-56. DOI:10.1007/s11770-010-0006-1 |
| [8] | Xia F, Ren Y Q, Jin S W. Tomographic migration-velocity analysis using common angle image gathers. SEG Technical Program Expanded Abstracts , 2008, 27: 3103-3106. |
| [9] | Kuo J T, Dai T F. Kirchhoff elastic wave migration for the case of noncoincident source and receiver. Geophysics , 1984, 49(8): 1223-1238. DOI:10.1190/1.1441751 |
| [10] | Sun R, McMechan G A. Pre-stack reverse-time migration for elastic waves with application to synthetic offset vertical seismic profiles. Proc. IEEE , 1986, 74(3): 457-465. DOI:10.1109/PROC.1986.13486 |
| [11] | Xue A M, McMechan G A. Prestack elastic Kirchhoff migration for multicomponent seismic data in variable velocity media. SEG Technical Program Expanded Abstracts , 2000, 19: 449-452. |
| [12] | Luth S, Buske S, Giese R, et al. Fresnel volume migration of multicomponent data. Geophysics , 2005, 70(6): s121-s129. DOI:10.1190/1.2127114 |
| [13] | Alkhalifah T, Tsvankin I, Larner K, et al. Velocity analysis and imaging in transversely isotropic media: Methodology and a case study. The Leading Edge , 1996, 15(2): 371-378. |
| [14] | Yan J, Sava P. Analysis of converted-wave extended images for migration velocity analysis. SEG Technical Program Expanded Abstracts , 2010, 29: 1666-1669. |
| [15] | Du Q Z, Li F, Ba J, et al. Multicomponent joint migration velocity analysis in the angle domain for PP-waves and PS-waves. Geophysics , 2012, 77(1): U1-U13. DOI:10.1190/geo2010-0423.1 |
| [16] | Qin N, Li Z C, Chen F Q, et al. A velocity tomography inversion method of elastic vector wavefield. 74th EAGE Extended Abstracts, 2012. |
| [17] | 秦宁, 李振春, 杨晓东. 基于角道集的井约束层析速度反演. 石油地球物理勘探 , 2011, 46(5): 725–731. Qin N, Li Z C, Yang X D. Tomography velocity inversion by well constraint based on the angle domain common imaging gathers. Oil Geophysical Prospecting (in Chinese) , 2011, 46(5): 725-731. |
| [18] | 秦宁, 李振春, 杨晓东, 等. 自动拾取的成像空间域走时层析速度反演. 石油地球物理勘探 , 2012, 47(3): 392–398. Qin N, Li Z C, Yang X D, et al. Image domain travel-time tomography velocity inversion based on automatic picking. Oil Geophysical Prospecting (in Chinese) , 2012, 47(3): 392-398. |
| [19] | 岳玉波.复杂介质高斯束偏移成像方法研究.青岛:中国石油大学, 2011. Yue Y B. Study on Gaussian beam migration methods in complex medium (in Chinese). Qingdao: China University of Petroleum, 2011. http://www.oalib.com/references/18990836 |
| [20] | Stork C. Reflection tomography in the postmigrated domain. Geophysics , 1992, 57(5): 680-692. DOI:10.1190/1.1443282 |
| [21] | 秦宁, 李振春, 杨晓东, 等. 高斯波束角道集的旅行时层析速度分析. 石油地球物理勘探 , 2013, 48(3): 366–371. Qin N, Li Z C, Yang X D, et al. Traveltime velocity tomography based on ADCIGs of Gaussian beam. Oil Geophysical Prospecting (in Chinese) , 2013, 48(3): 366-371. |
 2013, Vol. 56
2013, Vol. 56

