射线追踪是基于射线理论的地震模拟和成像技术的基础.不同的技术选择最优的射线追踪方法需要综合考虑算法的计算精度、计算效率、以及算法对复杂模型的适应能力等因素.地震走时层析成像作为一种复杂近地表地震速度反演方法,其关键技术之一是作为正演的射线追踪算法.作为一种迭代反演方法,层析反演过程需要反复实施走时正演计算,正演算法的精度和效率决定了整个反演流程的精度和效率;由于层析反演针对解决包含崎岖地表和强速度变化的近地表结构的模型,所以正演方法对复杂模型的适应能力尤为重要.因此,高效高精度并且能适应复杂模型的射线追踪方法是地震层析成像方法实用化必需的关键技术[1].
传统射线追踪方法有试射(Shooting)法和弯曲(Bending)法[2-4].试射法在数学上描述为一个初值问题,即从炮点以某初始角度出射射线,然后不断调整射线的出射角直至射线经过接收点.弯曲法在数学上描述为一个两点走时极值问题,即先给定两点间的初始路径,然后根据扰动理论对路径进行调整,直至两点间走时满足费马原理要求的最小走时.这两种方法在早期的地震勘探中被广泛应用,但每次计算只能得到一对炮检点之间的一条射线,故而对于单炮多道接收问题计算效率低.传统射线追踪思想和Dijkstra算法[5]结合产生了基于图形结构理论的最小走时算法及其改进算法[6-7],这些方法直接同时追踪得到多个接收点的射线路径.但该类方法的计算效率、计算精度、以及对复杂模型的适应性仍然很低,不能满足大规模复杂模型的计算要求.
射线追踪另一种思路是将波传播描述为波前面扩展,先将求取射线路径问题转化为求解描述波前面扩展的程函方程,然后从接收点沿地震波走时梯度方向追踪得到接收点和震源点之间的射线路径. Vidale最早实现了利用有限差分方法求解二维程函方程[8],并推广到求解三维模型[9].该方法首先用矩形网格将模型离散,用有限差分方法对程函方程进行离散化近似,然后从震源点开始,以矩形形式逐层向外扩展并用有限差分求解各网格走时.为了保证扩展过程符合因果律,每次从当前最小走时网格点所在的矩形边向外扩展.Podvin[10]在Vidale方法基础上,通过系统分析各计算网格点可能出现透射、折射、绕射等不同波传播形式,然后确定最终波前扩展,提高了该方法的精度.Vidale和Podvin应用的矩形扩展方式,在同一扩展面上只允许波前向外层传播,而不允许向内传播,在速度剧烈变化的复杂模型中可能与真实波前面传播方向不符.为了解决矩形扩展在复杂模型中可能违背因果规律的问题,Qin[11]引入Dijkstra算法思想研究从实际波前面进行扩展计算,大大提高了有限差分方法对复杂模型适应程度,提高了算法的稳定性.
FMM(Fast Marching Method)是目前公认效率最高、精度最高、且对任意复杂模型无条件稳定的射线追踪算法之一.FMM最早由Sethian[12-13]提出用于解决程函方程描述的曲线或曲面演化.其思想是利用满足波前演化"熵条件"的有限差分迎风格式求解程函方程,然后利用窄带技术快速实现波前扩展.
Sethian和Popovici[14]首次将该算法引入地球物理界用来求解地震走时问题.Popovici[15]进一步研究了该方法的高阶改进算法,提高了地震走时计算精度.近年来,FMM算法在计算精度和计算效率上都出现许多新的改进.在提高效率方面的改进主要是改进波前扩展实现所需的快速排序算法.在精度改进方面,除了采用更高阶的差分逼近方法之外,另一种方法是改变标准FMM方法只能利用计算点坐标轴方向相邻网格点进行计算的限制,研究利用对角方向网格点参与计算的方法.高阶差分的FMM方法虽然提高了FMM的计算精度,但是其误差分布和一阶差分一样存在明显的方向特征,即对角线方向误差大.Danielsson等[16]研究了以计算网格点所有邻点(包括对角邻点)建立单一差分格式,改善了算法的精度,但是该方法推广到高维高阶难度大.Hassouna等[17]提出了MSFM算法(Multi-stencils Fast Marching Methods),其原理是在标准FMM算法基础上通过坐标旋转产生多个FMM计算模板利用对角方向邻点参与计算.该方法相比标准FMM计算精度显著提高且容易推广到处理高维高阶问题.
自FMM被引入地球物理领域之后,该方法在地震层析反演中的射线正演、Kirchhoff深度偏移的走时表计算、时深转换的成像射线计算中被大量研究应用[18-20].本研究针对解决地震层析成像中的走时计算问题,由于层析成像解决的模型通常包含剧烈的地表起伏和近地表速度变化,本文重点研究MSFM在起伏地表模型中的实现.
起伏地表模型问题是目前我国西部地震勘探面临的难题,关于起伏地表模型的模拟和成像方法是目前亟待解决的地球物理问题[21-22].在起伏地表模型走时计算方法,兰海强等[23-24]研究了曲线坐标系下的程函方程求解,但该方法只适用于快速扫描法(FSM,fast sweeping method),而不适用于FMM方法.孙章庆等研究了复杂地表条件下线性插值和窄带技术结合的走时计算方法[25],以及不等距迎风差分法[26],并对比分析了阶梯网格迎风差分、不等距网格有限差分与混合网格线性插值方法在起伏地表模型走时计算中的性能[27].
本文引入MSFM算法用于解决地震走时层析成像反演中的射线正演.首先分析对比了MSFM方法和标准FMM的计算精度和计算效率;然后针对地震层析成像需要解决起伏地表模型问题,研究了MSFM算法针对起伏地表模型地震走时计算的实现方法,研究采用沿起伏地表对炮点邻近区域进行局部网格细分和在检波点邻近区域插值的方法尽量保持经典FMM方法的算法结构,以增加尽可能少的计算消耗来减小由于起伏地表产生的走时计算误差;最后以崎岖地表模型作为测试模型,进行了走时正演和层析反演试算.
2 算法原理和实现 2.1 FMM算法原理MSFM是FMM的改进算法,Hassouna的文章[17]详细推导了FMM方法到MSFM方法的改进,为叙述方便,在此以二维为例简要回顾FMM和MSFM的理论和实现过程.FMM算法将二维地震波前面扩展描述为:一条封闭曲线以给定的速度沿曲线法线方向向外运动演化.其数学形式即为程函方程:
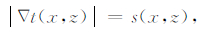
|
(1) |
其中t(x,z)为走时函数,s(x,z)为模型介质慢度函数.
求解方程(1),FMM采用有限差分迎风格公式
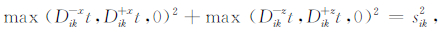
|
(2) |
其中Dik-xt、Dik+xt、Dik-zt、Dik+zt分别为x和z方向前向和后向差分算子,以一阶差分格式为例,有
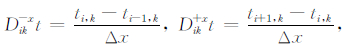
|
(3) |
Dik-zt、Dik+zt具有如上相同的形式.
将(3)式代入(2)式,整理得
其中Δ1=Δx,Δ2=Δz,且
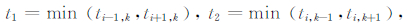
|
由(4)式可知方程(1)的解存在以下三种情况:
(1)若t>max(t1,t2),t为(4)式解的大值;
(2)若t2<t<t1,t=t1 +sΔ1;
(3)若t1<t<t2,t=t2 +sΔ2.
以上推导了一阶差分FMM方法实现,推广到高阶,其二阶格式为
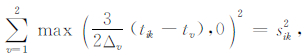
|
(5) |
其中Δ1=Δx,Δ2=Δz,且
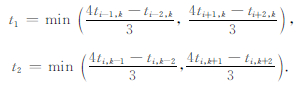
|
公式(4)和(5)所表达的一阶和二阶FMM可利用Dijkstra算法思想实现[11].
2.2 MSFM算法原理标准FMM计算模板只利用计算网格点轴向方法四个相邻网格点,MSFM利用坐标变换产生多个FMM计算的差分模板,实现了对角邻点参与计算.如图 1所示.计算点x四个对角邻点分别为p1、p2、q1、q2,其对角方向单位向量用r1、r2表示,则两个对角方向的旅行时方向导数可表示为
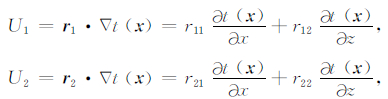
|
(6) |
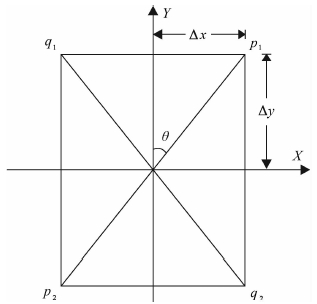
|
图 1 坐标旋转多模板示意图(参考文献[17]图 1) Fig. 1 The stencil of rotated coordinate system (refer to Paper[17] Fig. 1) |
写成矩阵形式为
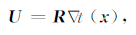
|
(7) |
其中
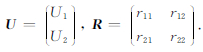
|
通过矩阵运算,可得
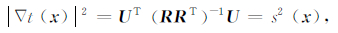
|
(8) |
若r1与r2间夹角为ϕ,有
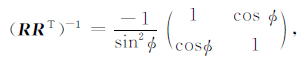
|
(9) |
代入(8)式,得
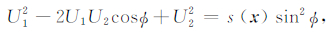
|
(10) |
方向偏导数用一阶差分逼近,有
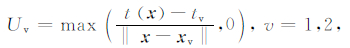
|
(11) |
其中
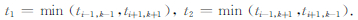
|
(11)式中xv为对角方向邻点走时较小的网格点位置,tv为xv位置网格点的走时,代入公式(10)即可解得t(x).
MSFM二阶格式与(11)式具有相同的形式,只需将差分格式(11)式改成如下二阶形式:
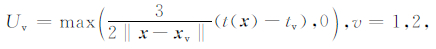
|
(12) |
其中
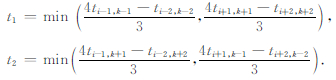
|
公式(11)和(12)为二维MSFM对角方向邻点的差分计算模板,和标准FMM模板联合,MSFM算法实现了多模板FMM计算,利用了计算网格点所有邻点.对比分析公式(4)、公式(5)、公式(11)和(12)MSFM算法保持了FMM的算法结构,MSFM程序可以在FMM程序框架下实现.
2.3 起伏地表MSFM实现方式层析成像技术是针对解决包含起伏地表的复杂模型速度建模的重要方法之一,故而与之配套的走时计算方法也必须能适应该类模型的计算要求.为此,本文重点研究了MSFM算法在起伏地表模型中的实现方式.为了保持经典FMM的算法框架,避免额外增加过多的计算量,我们采用沿起伏地表在炮点邻近区域局部细分网格,在检波点邻近区域直接插值的方法.
标准FMM算法实现利用Dijkstra算法思想,首先将计算网格点划分成三个子集,分别为走时已确定的已知点子集{known}、已经被计算但最终走时待定的窄带子集{narrow_band}和尚未被计算的远点子集{far}.其实现方法是:
(1)首先将炮点初始化已知点子集,走时为零;并根据FMM模板计算炮点所有在远点子集邻点的走时,并将这些点移入窄带子集.
(2)选取窄带子集中走时最小的网格点移入已知点子集,并用模板计算该点所有在窄带和远点子集内的邻点走时;若邻点在远点集中,则将该邻点移入窄带;若在窄带中,根据走时大小选择更新或者保持原走时值(保留较小走时).
(3)重复实施步骤(2)直至所有网格点移入近点集.
本文研究MSFM计算起伏地表模型的算法实现.在标准FMM实现划分三个子集基础上增加一个起伏地表之上网格点集{above_surface},如图 2所示,其算法实现伪代码如下:
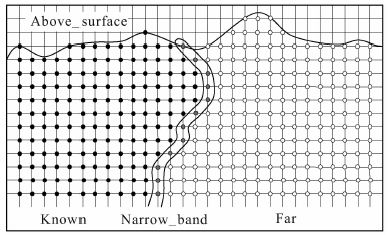
|
图 2 起伏地表模型FMM/MSFM算法实现示意图 Fig. 2 Implementation of FMM and MSFM in the model with topography |
(1)Initialize:
{above_surface}:地表之上区域点集,设定走时t=0;
{known}:走时已知点集,初始为震源点初始化走时t=0;
{narrow_band}:窄带点集,初始为震源邻点(包括对角方向),初始走时按直射线计算;
{far}:远点集,初始化走时t=∞.
(2)Loop:
a)查寻{narrow_band}集中最小走时点P,转入{known}集;
b)计算P点所有{narrow_band}和{far}中邻点走时,分别计算两个模板得到的走时t1和t2,取max(t1,t2)更新该网格点走时;若邻点为远点,转入{narrow_band}集;
c)若{narrow_band}=ø,则结束循环;否则返回继续循环.
上述算法流程在规则网格中实现,规则网格无法准确描述不规则起伏界面和不规则炮检点分布.细分网格可以提高对不规格界面的刻画,但整个计算域细分网格,意味着计算量成倍增加(详见下节效率分析).考虑到实际地震采集炮检点通常布设于地表或者地下某个深度,炮检点起伏变化基本与地表起伏一致,并且MSFM方法最大的误差分布在炮点附近(详见下节精度分析),因此只需对炮检点附近网格细分处理即可同时达到精细刻画起伏地表和炮检点位置,并且提高整体计算精度的目的.前人提出了多种精细处理炮点附近计算域方法,如Alkhalifah等[28]提出的以炮点为中心建立球坐标网格方法,以及局部网格细分方法等.
本文采用Rawlinson等[19]提出的改进局部细分网格方法,将之改进用来处理起伏地表.如图 3左图所示中心实心大圆点为炮点,三角符号为正常计算网格点,小圆点为炮点四周细分后的网格点,虚线为地表曲线.实现过程为首先以炮点为中心给定一个矩形的区域,对该区域细分网格,在该区域内基于细网格计算波前面,如左图实线所示为波前面,其包围的实心点为已经确定走时的网格.一旦矩形边界上的某个正常网格点走时被确定(如左图A点),立即停止基于细分网格的走时计算,抽取已确定走时的正常网格点(右图),然后在正常的网格点上继续计算.以上论述了炮点附近网格细分处理,检波点按上述方法处理涉及复杂的插值计算,简单易行的处理方法是直接由计算网格点插值得到检波点位置的走时.为了不额外增加过多计算量,本研究采用直接插值方法处理检波点位置.
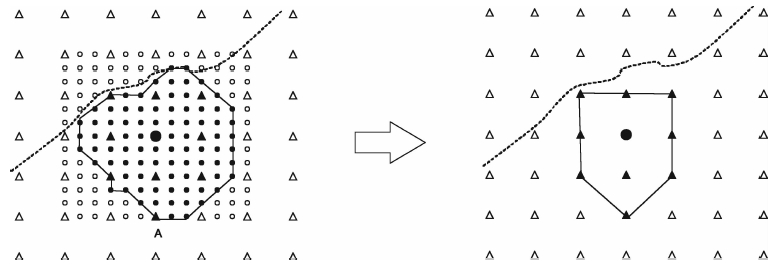
|
图 3 起伏地表炮点附近区域局部网格细分算法实现示意图 Fig. 3 Illustration of local grid refinement near source in the model with topography |
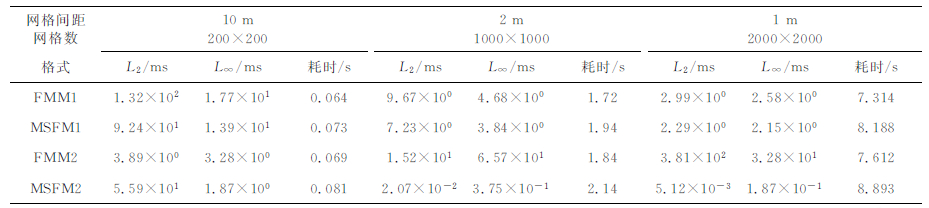
为了验证本文算法的精度和效率,我们设计一个横向宽度2km、纵向深度2km、波速1000 m/s的均匀模型.我们分别采用三种网格间距离散模型同时采用四种格式计算比较分析算法的精度和效率.精度指标采用计算结果与解析解误差的L2范数和L∞范数.
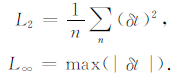
|
(13) |
其中n为计算节点数,δt为走时误差.
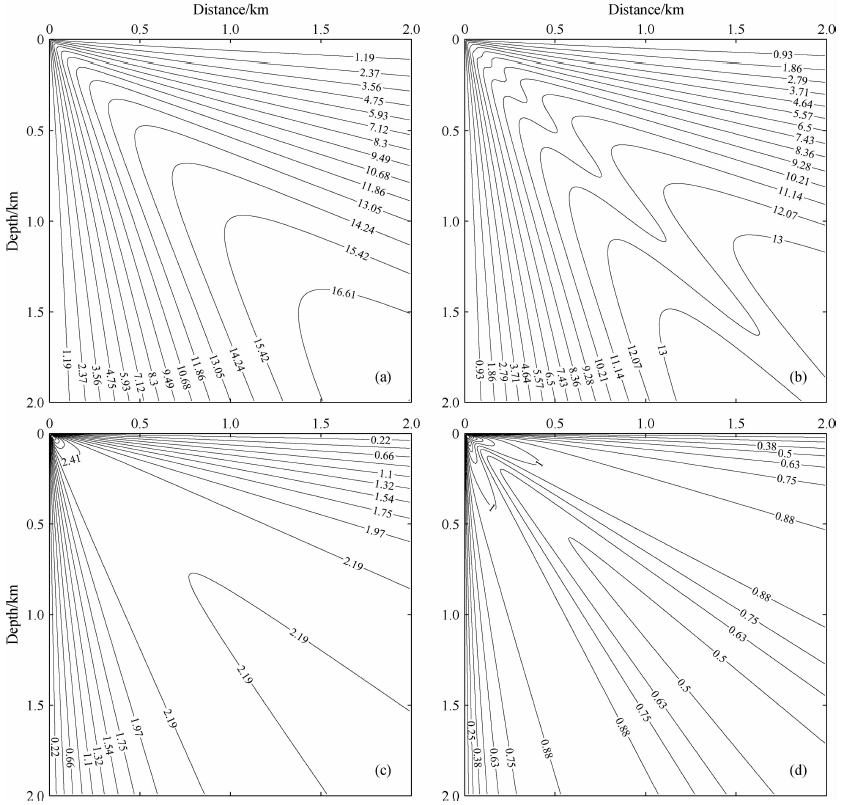
表 1列出了1、2、10 m三种网格间距,一阶FMM(FMM1)、二阶FMM(FMM2)、一阶MSFM(MSFM1)和二阶MSFM(MSFM2)四种格式的计算精度和计算时间.分析表中L2范数和L∞范数变化规律可知:四种格式整体误差和最大误差FMM1>MSFM1>FMM2>MSFM2,并且随着网格间距变小,误差变小.总体来说,四种格式都具有很高的精度,即使在10m网格间距离散的情况下,FMM1和MSFM1最大误差都在10ms量级上,而FMM2和MSFM2精度更高,MSFM2比FMM1高出一个数量级的精度.图 4显示了10m网格离散时四种格式的误差分布,由图可见FMM大误差主要在对角线,MSFM相对相同阶次的FMM明显改善了对角方向的误差.另外误差分布等值线显示随着传播距离增大误差没有明显累积,尤其对于二阶格式,最大误差在源点附近即已存在,由此可见,对源点附近区域进行细分网格可明显改善整体的计算精度.
|
|
表 1 四种格式计算精度和效率对比分析表 Table 1 Analysis of accuracy and deficiency of four formulas |
|
图 4 10m×10m间距离散网格模型计算误差分布等值线图 (a) FMM1结果;(b) MSFM1结果;(c) FMM2结果;(d) MSFM2结果.走时误差值单位:ms. Fig. 4 Contours of error values calculated in the model with 10 m×10 m discrete grids The results of (a) FMM1; (b) MSFM1; (c) FMM2; (d) MSFM2. The unit of values is ms. |
表 1同时列出了不同计算网格下四种格式的计算时间,分析表中数据可见对于本算例规模大小的模型MSFM算法相比同阶次FMM大约增加10%的计算时间.从理论上分析,FMM和MSFM具有相同的算法结构,都通过Dijstra算法思想实现波前面的扩展.FMM类算法计算消耗主要有两部分:一部分来自计算差分格式,另一部分来自Dijstra算法的排序操作.经典FMM通过优先队列实现窄带内网格点的移除和插入操作,通过堆排序实现优先队列移除和插入的时间复杂度为Ο(logNNB),其中NNB为窄带内点数.由于通常情况NNB ≪ N(N为总计算网格点数),该算法时间复杂度最差为Ο(NlogN),所以FMM类方法计算效率非常高. MSFM相比FMM,需要计算两个差分模板,计算差分格式消耗时间应是同阶FMM格式的2倍,但由于两种方法对窄带移除和插入操作数基本相同,因此,两种方法整体计算时间消耗比率应在1~2倍之间.对于更大规模的复杂模型,用于维持窄带点集队列结构的移除和插入操作所消耗时间在整体计算消耗中所占的比重更高,MSFM和FMM在效率上表现将更接近.
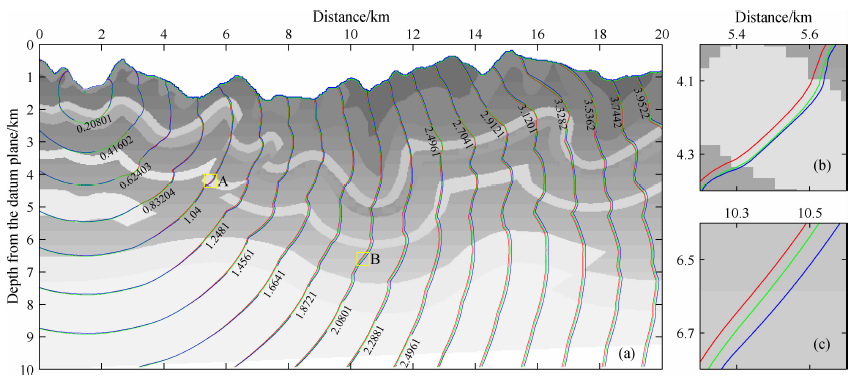
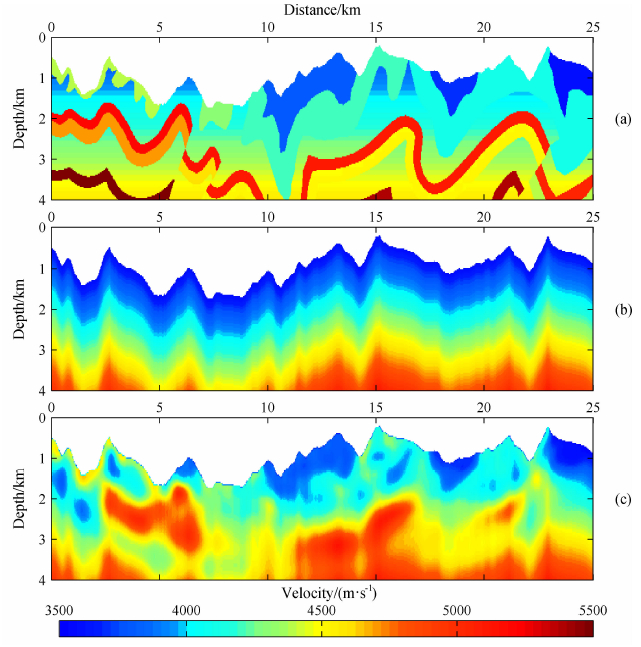
4 算例为了验证本文方法在复杂模型中的计算效果,我们对崎岖地表模型进行走时正演试算,并将本文方法作为走时计算方法进行初至走时层析反演.图 5显示了崎岖地表模型某点源激发的走时计算结果.由于复杂模型无法解析地计算得到完全精确的走时值,利用FMM算法计算网格间距越小计算精度越高的特点,我们首先将模型离散成5 m×5 m的数值计算网格,应用一阶FMM格式计算走时,将该走时值作为精确解的参考值;然后,将模型离散成30m×30m的数值计算网格,分别应用一阶FMM格式和一阶MSFM格式计算走时进行对比.图 5a显示了粗网格离散时两种方法计算得到走时等值线和精确走时参考值等值线的叠合图,其中红线为粗网格一阶FMM格式计算结果,绿线为粗网格一阶MSFM格式计算结果,蓝线为精确走时参考值(即细网格一阶FMM结果),由图可见两种方法的计算结果在整体上都和精确走时参考值具有很高的一致性.图(b)和图(c)分别为图(a)中标注为A和B的黄色矩形区域的放大显示.图(b)显示(A区域和震源横向偏移距约4km)粗网格FMM计算结果(红线)和参考值(蓝线)存在很小的误差,而粗网格MSFM的结果(红线)和参考值几乎完全吻合,说明同等计算网格间距下MSFM比FMM具有更高的计算精度.图(c)显示随着偏移距增大(B区域和震源横向偏移距约9km),两种方法的误差都随之增大,但MSFM方法仍然保持比FMM更高的计算精度.在本算例的计算消耗上,粗网格离散时FMM和MSFM的内存消耗和计算时间几乎相同.然而,细网格(5m)离散的模型网格数是粗网格(30m)的36倍,与之相应前者计算内存消耗也是后者的约36倍,而前者的计算时间则是后者的约40倍.由此表明,本文方法可以在较粗离散网格条件下得到和标准FMM在很细离散网格下相同的计算精度,大大节省了程序的内存开支和计算时间.图 6展示了利用本文算法作为走时计算方法的初至层析反演结果.图(a)、(b)、(c)分别为崎岖地表模型的真实模型、反演初始模型,以及反演结果的浅层部分,结果可见浅层速度结构中的大尺度成分被很好地恢复重建.模型试算结果表明MSFM能很好应用于复杂模型正演和反演的走时计算.
|
图 5 崎岖地表模型走时正演计算结果 (a)走时等值线图;(b)图(a)A位置矩形区域放大显示;(c)图(a)B位置矩形区域放大显示.红线为30 m×30 m网格一阶FMM计算结果,绿线为30 m×30 m网格一阶MSFM计算结果,蓝线为5 m×5 m网格一阶FMM计算结果.走时值单位:s. Fig. 5 Result of travel-time calculations in the model with irregular topography (a) Contours of travel-time; (b) enlarged view of boxed area labeled A in lett figure; (c) enlarged view of area B. Red line indicate result calculated in the model with 30 m× 30 m discrete grids by FMM1, green line indicate result calculated in 30 m× 30 m discrete grids by MSFM1, blue line indicate result calculated in 5 m×5 m discrete grids by FMM1. The unit of travel-time s second. |
|
图 6 采用本文方法计算走时的崎岖地表模型初至层析反演结果 (a)理论模型;(b)初始模型;(c)反演结果. Fig. 6 Result of tomography for model with rregular topography in which the proposed method s applied to travel-time calculation (a) True model; (b) Initial model; (c) Result of tomography. |
FMM作为一种高效率高精度的走时算法已经在地震走时计算中被广泛应用,本文研究采用的MSFM算法利用坐标旋转实现多模板FMM计算,改善了FMM的计算精度,同时保持了FMM算法的高效性.本文将该方法引入到复杂起伏地表模型走时层析的正演计算中,通过分析和模型试算表明MSFM方法能为走时层析反演提供高效高精度的正演计算,能很好适用于复杂模型.MSFM方法可作为地震走时层析反演中一种高效高精度的正演技术,有很好的应用价值.
| [1] | Nolet G. Seismic tomography. Dordrecht: D. Reidel, 1987 . |
| [2] | Um J, Thurber C. A fast algorithm for two-point seismic ray tracing. Bulletin of the Seismological Society of America , 1987, 77(3): 972-986. |
| [3] | Moser T J, Nolet G, Snieder R. Ray Bending Revisited. Bulletin of the Seismological Society of America , 1992, 82(1): 259-288. |
| [4] | Langan R T, Lerche I, Cutler R T. Tracing of rays through heterogeneous media: An accurate and efficient procedure. Geophysics , 1985, 50(9): 1456-1465. DOI:10.1190/1.1442013 |
| [5] | Dijkstra E W. A Note on Two Problems in Connection with Graphs. Numerische mathematik , 1959, 1: 269-271. DOI:10.1007/BF01386390 |
| [6] | Moser T J. Shortest path calculation of seismic rays. Geophysics , 1991, 56(1): 59-67. DOI:10.1190/1.1442958 |
| [7] | 王辉, 常旭. 基于图形结构的三维射线追踪方法. 地球物理学报 , 2000, 43(4): 534–541. Wang H, Chang X. 3-D ray tracing method based on graphic structure. Chinese J. Geophys. (in Chinese) , 2000, 43(4): 534-541. |
| [8] | Vidale J. Finite-Difference Calculation of Travel-Times. Bulletin of the Seismological Society of America , 1988, 78(6): 2062-2076. |
| [9] | Vidale J E. Finite-difference calculation of traveltimes in three dimensions. Geophysics , 1990, 55(5): 521-526. DOI:10.1190/1.1442863 |
| [10] | Podvin P, Lecomte I. Finite difference computation of traveltimes in very contrasted velocity models: a massively parallel approach and its associated tools. Geophysical Journal International , 1991, 105(1): 271-284. DOI:10.1111/gji.1991.105.issue-1 |
| [11] | Qin F H, Luo Y, Olsen K B, et al. Finite-difference solution of the eikonal equation along expanding wave-fronts. Geophysics , 1992, 57(3): 478-487. DOI:10.1190/1.1443263 |
| [12] | Sethian J A. A fast marching level set method for monotonically advancing fronts. Proceedings of the National Academy of Sciences of the United States of America , 1996, 93(4): 1591-1595. DOI:10.1073/pnas.93.4.1591 |
| [13] | Sethian J A. Fast marching methods. Siam Review , 1999, 41(2): 199-235. DOI:10.1137/S0036144598347059 |
| [14] | Sethian J A, Popovici A M. 3-D traveltime computation using the fast marching method. Geophysics , 1999, 64(2): 516-523. DOI:10.1190/1.1444558 |
| [15] | Popovici A M, Sethian J A. 3-D imaging using higher order fast marching traveltimes. Geophysics , 2002, 67(2): 604-609. DOI:10.1190/1.1468621 |
| [16] | Danielsson P E, Lin Q. A modified fast marching method // Image Analysis. Springer Berlin Heidelberg, 2003: 1154-1161. |
| [17] | Hassouna M S, Farag A A. Multistencils fast marching methods: A highly accurate solution to the eikonal equation on Cartesian domains. Ieee Transactions on Pattern Analysis and Machine Intelligence , 2007, 29(9): 1563-1574. DOI:10.1109/TPAMI.2007.1154 |
| [18] | Cameron M, Fomel S, Sethian J. Time-to-depth conversion and seismic velocity estimation using time-migration velocity. Geophysics , 2008, 73(5): VE205-VE210. DOI:10.1190/1.2967501 |
| [19] | Rawlinson N, Sambridge M. Multiple reflection and transmission phases in complex layered media using a multistage fast marching method. Geophysics , 2004, 69(5): 1338-1350. DOI:10.1190/1.1801950 |
| [20] | Rawlinson N, Sambridge M, Saygin E. A dynamic objective function technique for generating multiple solution models in seismic tomography. Geophysical Journal International , 2008, 174(1): 295-308. DOI:10.1111/gji.2008.174.issue-1 |
| [21] | 兰海强, 刘佳, 白志明. VTI介质起伏地表地震波场模拟. 地球物理学报 , 2011, 54(8): 2072–2084. Lan H Q, Liu J, Bai Z M. Wave-field simulation in VTI media with irregular free surface. Chinese J. Geophys. (in Chinese) , 2011, 54(8): 2072-2084. |
| [22] | 张浩, 张剑锋. 起伏地表采集数据的三维直接叠前时间偏移方法. 地球物理学报 , 2012, 55(4): 1335–1344. Zhang H, Zhang J F. 3D prestack time migration including surface topography. Chinese J. Geophys. (in Chinese) , 2012, 55(4): 1335-1344. |
| [23] | 刘一峰, 兰海强. 曲线坐标系程函方程的求解方法研究. 地球物理学报 , 2012, 55(6): 2014–2026. Liu Y F, Lan H Q. Study on the numerical solutions of the eikonal equation in curvilinear coordinate system. Chinese J. Geophys. (in Chinese) , 2012, 55(6): 2014-2026. |
| [24] | 兰海强, 张智, 徐涛, 等. 贴体网格各向异性对坐标变换法求解起伏地表下地震初至波走时的影响. 地球物理学报 , 2012, 55(10): 3355–3369. Lan H Q, Zhang Z, Xu T, et al. Effects due to the anisotropic stretching of the surface-fitting grid on the traveltime computation for irregular surface by the coordinate transforming method. Chinese J. Geophys. (in Chinese) , 2012, 55(10): 3355-3369. |
| [25] | 孙章庆, 孙建国, 韩复兴. 复杂地表条件下基于线性插值和窄带技术的地震波走时计算. 地球物理学报 , 2009, 52(11): 2846–2853. Sun Z Q, Sun J G, Han F X. Traveltimes computation using linear interpolation and narrow band technique under complex topographical conditions. Chinese J. Geophys. (in Chinese) , 2009, 52(11): 2846-2853. |
| [26] | 孙章庆, 孙建国, 韩复兴. 三维起伏地表条件下地震波走时计算的不等距迎风差分法. 地球物理学报 , 2012, 55(7): 2441–2449. Sun Z Q, Sun J G, Han F X. Traveltime computation using the upwind finite difference method with nonuniform grid spacing in a 3D undulating surface condition. Chinese J. Geophys. (in Chinese) , 2012, 55(7): 2441-2449. |
| [27] | 孙章庆, 孙建国, 韩复兴. 针对复杂地形的三种地震波走时算法及对比. 地球物理学报 , 2012, 55(2): 560–568. Sun Z Q, Sun J G, Han F X. The comparison of three schemes for computing seismic wave traveltimes in complex topographical conditions. Chinese J. Geophys. (in Chinese) , 2012, 55(2): 560-568. |
| [28] | Alkhalifah T, Fomel S. Implementing the fast marching eikonal solver: spherical versus Cartesian coordinates. Geophysical Prospecting , 2001, 49(2): 165-178. DOI:10.1046/j.1365-2478.2001.00245.x |
 2013, Vol. 56
2013, Vol. 56