电离层作为卫星信号传播的特殊介质，对卫星通信和导航定位等空间活动有着十分重要的意义.电离层不规则体可导致无线电波穿过电离层时发生闪烁，其空间尺度从几米到上千公里，持续的时间长度也因所处的纬度和季节等因素有所不同.Spread-F是夜间F层电子和离子密度的一种不规则扰动，在电离图上表现为描迹的扩展^[1]，现在普遍认为导致F层不规则结构生成的基本机制是重力-瑞利-泰勒不稳定性（简称R-T不稳定性）^[2].

大量研究工作表明，重力波是触发电离层spread-F的种子因素之一^[3].Kelley ^[4-6]等人指出，大尺度赤道spread-F是受等离子体不稳定性和重力波的共同影响产生的；黄朝松^[7]等人从理论上证明了重力波能触发R-T不稳定性并导致等离子体泡形态；肖赛冠^[8]等人利用高频多普勒观测数据，从形态学角度直接揭示了声重力波激发中纬spread-F的种子作用.数值模拟结果表明，重力和初始扰动^[9-11]、电场扰动^[12]以及背景中性风扰动^[13]都可能激发电离层不稳定性.

除上述自然扰动能够产生spread-F外，人工手段也可能激发电离层spread-F.1990年NASA和Boston大学联合进行了两次利用化学物质SF₆来激发R-T不稳定性的实验，释放高度选在赤道电离层底部，两次均在人工扰动区域观测到了赤道扩展F（Equatorial Spread-F，ESF）的形成，证明了利用化学物质来人工激发电离层不稳定性的可能性^[14].

本文建立了中低纬spread-F发展的物理模型，包括了中性风、电场以及压力作用，并对spread-F的形态进行了数值模拟研究，讨论了利用化学物质H₂O释放来激发电离层不稳定性的可能性.

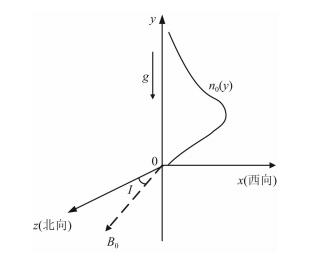
采用图 1所示的直角坐标系，x轴指向西，y轴垂直地面向上，z轴指向北，不考虑磁偏角，地磁场在yz平面内，在电离层F区，离子成分主要考虑O⁺，描述电子和离子运动的基本方程为

图 1

Fig. 1

图 1 背景电子密度 Fig. 1 Bac kground electron density

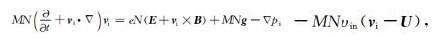
(1)

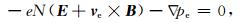
(2)

其中M是离子的质量，N为离子（电子）数密度，e为电荷量，v_i是离子速度，v_e是电子速度，U是中性风的速度，E为电场，B是地磁场，g是重力加速度，υ_in是离子与中性粒子的碰撞频率，压力项p_i=NkT_i，k为玻耳兹曼常数，T_i是离子温度，并假定电子温度与离子温度相等，记为T.电子的连续性方程为

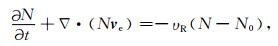
(3)

电流连续性方程为

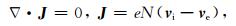
(4)

式中υ_R为复合系数，N₀是平衡态的数密度，J为电流.记E=E₀ -∇ϕ，E₀是平衡态电场，ϕ是扰动电势，利用方程（1）和（2），忽略离子动量方程左端的惯性项，得到离子和电子的速度分别为

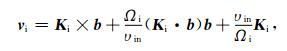
(5)

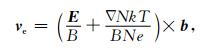
(6)

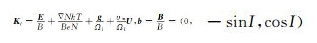
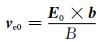
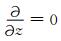
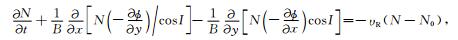
其中，I是磁倾角，Ω_i为离子回旋频率.将（6）式代入电子连续性方程，在以电子零级漂移速度运动的参考坐标系中，不考虑北向电场和风场的作用，且，并假定υ_in，υ_R和N₀只是高度y的函数.化简得

(7)

代入电流连续性方程化简得

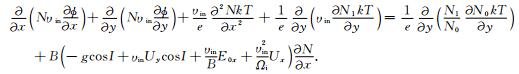
(8)

（7）（8）两式就是中低纬spread-F发展的控制方程.为了求解方程组的非线性解，令Q=N/N₀，方程（7）、（8）变为

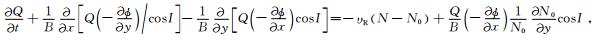
(9)

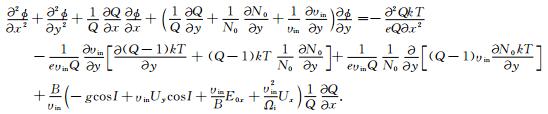
(10)

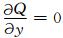
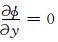
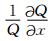
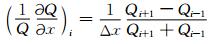
方程（10）是椭圆方程，采用交替隐式法（ADI）求解^[15]，方程（9）是双曲线方程，采用通量修正方法（FCT）求解^[16].背景电离层参数由IRI-2007模式^[17]得到，中性大气参数由NRLMSISE-00模式^[18]得到.数值计算中采用二维正交网格，水平和垂直方向的网格数分别为103和101，空间步长分别为1 km和3 km，水平方向Q和ϕ采用周期边界条件，竖直方向上采用，边界条件，时间步长为2 s.对于形如的格式，采用中心差分近似代替，即（以第i网格点为例，Δx为x方向步长）.

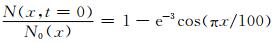
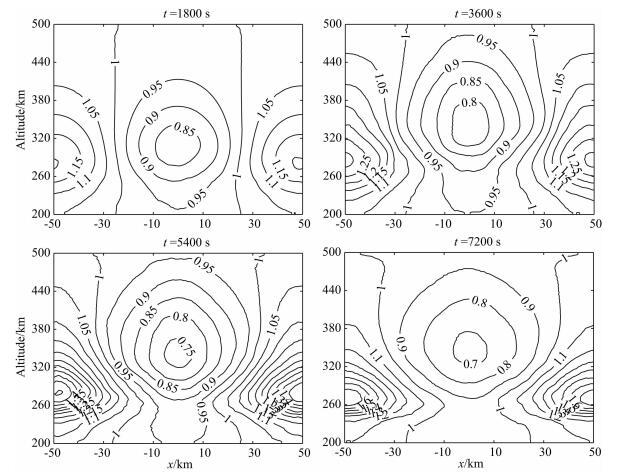
释放的区域选择在南京地区（地理坐标：32°N，118.5°E，磁倾角为47.3°），地磁场强度取为3× 10^-5 T，初始时刻为太阳活动低年7月份21LT.在很多的模拟工作中^{[9-11, 13]}，将5%的正弦扰动即作为spread-F自然发生时的初始条件.没有水平电场的作用时，初始扰动会很快稳定下来，电场强度较低时，等离子体泡的上升速度较慢，电子密度的扰动幅度也较小. 图 2给出了水平电场强度为-3×10^-3 V/m时，不同时刻的电离层电子密度归一化分布.1800 s时扰动中心附近电子密度显著减少，最大消耗约为20%，而在中心两侧出现了电子密度的增强现象，形成了明显的等离子体泡结构，到3600 s时，等离子体泡进一步上升到达峰值高度附近，上升速度大约为16.7 m/s，5400 s时电子的消耗幅度可达30%，两侧的增幅可达50%.

图 2

Fig. 2

图 2 在5%初始正弦扰动后不同时刻的电子密度归一化分布（E0x=-3×10-3 V/m） Fig. 2 Normalized electron density distribution at different time under the 5% sine initial disturbance (E0x=-3×10-3 V/m)

由于电离层中分子性离子与电子的复合要比氧离子与电子的辐射性复合快得多，中性气体的释放可造成电子的大量消耗，形成可观的电离层空洞. H₂O在电离层高度释放后，主要发生如下离子化学反应：

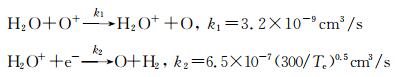
其中k₁和k₂分别为反应系数.18 kg的H₂O在电离层底部242 km高度处点源释放后，迅速向四周扩散并发生离子化学反应，5 min后释放中心附近的电子密度降幅可达40%.把此时的电离层状态作为spread-F发展的初始扰动条件，不考虑风场的影响，仅在-3×10^-3 V/m水平电场的作用下，电离层空洞不断上升，耗空幅度不断加大，上升速度约为66.7 m/s，如图 3所示，1000 s时电子分布形态已不再是初始“椭圆”形态，2000 s后等离子体泡顶部已穿过峰值高度，最大的耗空幅度~40%，两侧的密度增幅可达~30%.图 4是扰动电势的空间分布，释放中心两侧扰动电势的符号相反，结构基本对称，电势的峰值高度也在不断地抬升，2000 s时扰动电势可达~15 V，量级与背景电场相当.在电离层底部释放化学物质时，电子的大量消耗使得电子密度的梯度变得更大，有利于电离层R-T不稳定性的激发，产生spread-F.

图 3

Fig. 3

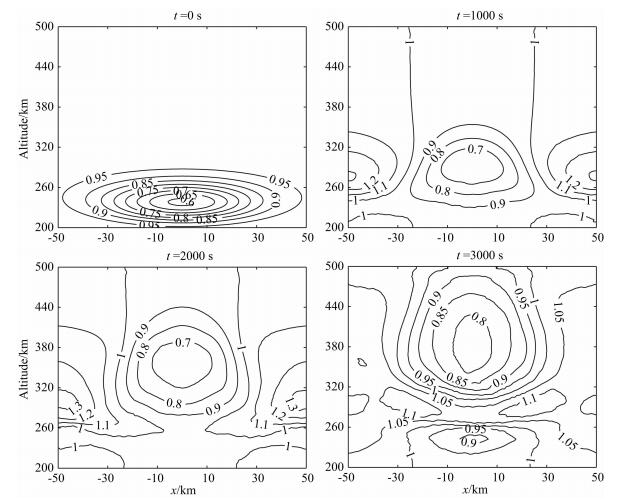
图 3 化学物质在底部释放扰动后不同时刻的电子密度归一化分布（E0x=-3×10-3 V/m） Fig. 3 Normalize delectron density distribution at different time under the initial disturbance of chemical bottomside release (E0x=-3×10-3 V/m)

图 4

Fig. 4

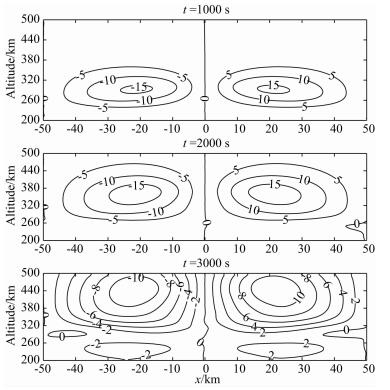
图 4 化学物质在底部释放扰动后不同时刻的扰动电势空间分布 Fig. 4 Electric potential distribution at different time under the initial disturbance of chemical bottom side release

水平电场为-3×10^-4 V/m时，依据谢红^[19]等人推导的中低纬电离层F区中有碰撞的R-T不稳定性的线性增长率，此时的电离层是比较稳定的.存在5%的正弦扰动时，2000 s时最大耗空约为4%，6000 s时为3%，到12000 s时电子的最大扰动幅度只有1%，扰动逐渐趋于稳定，如图 5（a，b，c）所示.图 5（d，e，f）是18 kg的H₂O在电离层底部释放后的电子分布，在电场作用下等离子体泡有一定上升，2000 s时中心可达260 km，6000 s时上升到290 km左右，电子的最大消耗幅度可达6%，两侧出现了密度增强区域，但电子的最大扰动幅度逐渐减少，到12000 s时为3%左右，扰动也不断趋于稳定化，虽然没有出现spread-F的发展，但其仍能造成较长时间和较大范围的电离层扰动.

图 5

Fig. 5

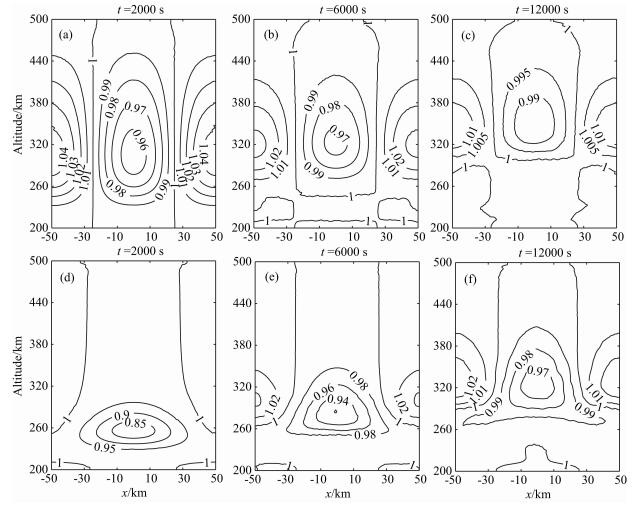
图 5 不同初始扰动条件下不同时刻的电子密度归一化分布 Fig. 5 Normalized electron density distribution at different time under different initial disturbances

本文利用离子和电子动量方程、连续性方程以及电流连续性方程建立了适合中低纬spread-F发展的物理模型，并对spread-F的形态进行了数值模拟研究，讨论了利用化学物质释放来人工激发电离层R-T不稳定性的可能性.电离层处于不稳定状态时，H₂O在电离层底部释放后，造成电子大量的消耗，增强了峰值高度以下的电子密度梯度，有利于spread-F的发展，在spread-F的发展过程中，扰动中心附近会形成电子密度的消耗区，两侧出现密度的增强区.而电离层比较稳定时，初始扰动会逐渐稳定下来，但化学物质的释放仍能造成电子密度较长时间、较大范围的扰动，表明化学物质释放可作为人工激发电离层R-T不稳定性的有效手段.

在本文的模拟中，为了计算的简便，将化学物质释放5min后造成的电离层“空洞”作为spread-F发展的初始扰动条件，没有考虑化学物质的后续效应以及对spread-F的影响，即两者的相互耦合作用，这将是下一步研究的方向.