磁共振测深(MagneticResonanceSounding,简称MRS)是一种应用核磁共振现象探测地下水的地球物理方法[1-2],与其他物探方法相比具有非侵入性和能够直接定量探测地下水的特点.在磁共振测深方法[3-4]中,地下水中氢质子在地磁场的环境下处于平衡状态,在地面铺设线圈中通入当地拉莫尔频率的交变电流产生激发磁场,氢质子受磁场激发产生能级跃迁,激发停止后在线圈中接收到氢质子由激发态恢复到平衡态过程中产生的MRS信号.
磁共振测深的反演是通过MRS信号初始振幅和平均弛豫时间T 2*来反映地下含水量的大小及含水层平均有效孔隙大小[5].Legchenko[6]于1998年提出利用MRS信号不同脉冲矩下的初始振幅进行反演,仅能得到随深度变化的含水量结果.随着技术的发展,Mohnke[7]在2002年提出了平滑反演和分块反演方法,能快速得到地下含水量和平均弛豫时间.基于此,人们开展了大量的线性反演和非线性反演算法研究.翁爱华等[8]于2005年采用非线性反演技术得到层状大地的MRS含水量垂向分布.戴苗[9]于2009年采用奇异值分解和模拟退火方法实现了MRS平滑反演.随着研究的不断深入和应用的日益广泛,这两种传统反演方法固有的缺点也逐渐显现,并成为制约MRS技术进一步发展的瓶颈.首先,平滑和分块均需要通过获取初始振幅信息进行反演,由于仪器死区时间的客观存在,初始振幅需通过单一指数拟合后延拓得到,含水量反演结果受噪声干扰及拟合程度影响严重;其次,反演得到的平均弛豫时间T2*仅反映含水层平均孔隙度情况,不利于多孔隙地质环境的解释.
地面MRS多弛豫时间反演起步于2005年.Mohnke[10]提出了时间步长反演方法,利用信号随时间变化的测深曲线,得到不同时间下含水量与深度的关系,实现了多弛豫时间反演.但该方法过度依赖于含水量时间曲线,结果极不稳定.Mike等[11]考虑反演模型垂向平滑问题,研究了一种稳定的QT算法,不过由于平滑约束的固有特点,出现含水层边界面刻画模糊,反演结果不清晰、迭代耗时长等缺陷.
本文针对目前国内外磁共振反演方法的不足,结合MRS信号整体性与多指数特性,借鉴分层反演的思想,首次提出并实现了磁共振全弛豫数据分层多指数反演方法.采用多指数拟合方式将MRS信号所有采集数据一次性带入反演,直接建立起地下探测深度、弛豫时间、含水量三个重要参数的关系.该方法通过构建泛函极小值方程,利用不等式约束的空间信赖域算法进行优化,可快速、精确的反演获得各含水层位置、弛豫时间及其对应含水量等信息.
为全面验证本文提出的反演方法,文中首先建立了多含水层单一孔隙和多含水层多孔隙两种不同的地下水模型.反演分别采用平滑、分块和分层多指数三种方法依次进行,并从模型逼近程度,目标值拟合误差等方面展开对比分析.最后,笔者对白城四方坨子测试点的磁共振野外实测数据进行反演解释,估算了涌水量[12-13]的大小,与钻井资料进行一致性比对.本研究通过模型数据与实测数据,充分证实了该反演方法的优越性.
2 磁共振数据反演方法 2.1 磁共振信号初始振幅反演磁共振是具有非零磁矩的原子核在交变磁场的作用下发生共振吸收的现象.计算地下水中氢原子核的磁共振角频率ω0公式为
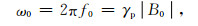
|
(1) |
其中,B0是测试地点的静地磁场;γp=0.267518 Hz/nT是氢质子的旋磁比;f0是当地氢质子的拉莫尔频率[14].为测量MRS信号,在测试地点铺设线圈,线圈的直径大小取决于所要探测的最大深度.线圈中通入当地拉莫尔频率的交变电流,在地下形成激发磁场.公式为
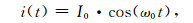
|
(2) |
其中,I0为电流强度,激发持续时间0<t<τ,由脉冲矩q=I0τ体现激发强度.激发停止后,地面接收线圈感应到磁共振响应信号,方程为
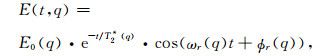
|
(3) |
其中,ωr和ϕr分别代表接收信号的角频率和相位;平均弛豫时间T2*反映地下平均有效孔隙大小;信号的初始振幅E0表示在激发停止时刻磁共振信号的幅值大小,它与地下含水量直接相关.磁共振信号的包络称为自由感应衰减(FreeInductionDecay,简称FID)信号,呈指数规律衰减.Weichman[15]等人提出通过方程(4)描述FID信号,建立信号初始振幅与含水量的关系:
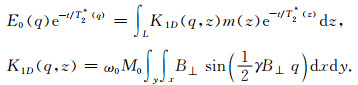
|
(4) |
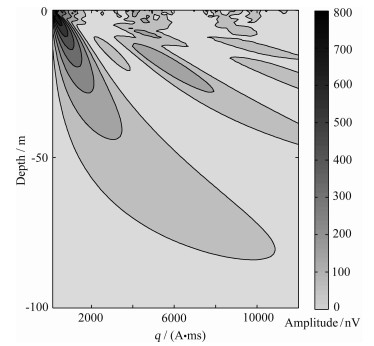
其中,L代表了地下水探测的深度范围;K1D(q,z)是一维核函数[16],描述不同脉冲矩下不同深度处核磁共振信号的响应,反映了激发磁场的穿透能力及分辨率,体现地下磁共振响应的灵敏度,如图 1所示,横轴代表激发脉冲矩,纵轴代表地下深度,颜色代表了响应强度;M0是氢原子核的磁化强度,代表平衡条件下单位体积内的磁矩;B⊥是激发磁场垂直于地磁场的分量;0≤m(z)≤1代表地下含水量情况.按深度z将方程(4)离散化,得到了初始振幅与含水量之间的矩阵关系为
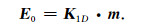
|
(5) |
|
图 1 传统一维核函数图 Fig. 1 Traditional one dimensional kernel matrix |
平滑反演方法是将地下从地表至最大探测深度通过等间距或递增间距的方式使地下含水层呈层状分布,公式为
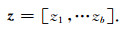
|
(6) |
采用吉洪诺夫正则化[17-18]方法计算每个含水层对应的含水量m(zi)及平均弛豫时间T2*(zi),i=1,…,b.其吉洪诺夫泛函极小值方程为
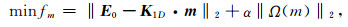
|
(7) |

|
(8) |
其中,T2cal*=-td/(lnE1 -ln(K1D·m)).E1是经过仪器死区时间td后的信号幅值;α>0为正则化参数,Ω(z)是正则化因子.平滑反演通过单一指数拟合得到不同激发脉冲矩下的信号幅值E1(td)及T2*,根据公式(9)延拓计算初始振幅E0,求解方程(7)和方程(8),获得地下总含水量及平均弛豫时间T2*的垂向分布.公式为
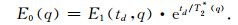
|
(9) |
分块反演的整个过程与平滑反演类似,不同之处在平滑反演预设地下含水层按深度z呈层状分布,而分块反演是已知地下含水层个数,各含水层深度未知,需要反演获得,其结果使得各含水层之间分界明显,易于判断含水层位置.
2.2 磁共振弛豫信号的多指数描述目前,磁共振平滑反演与分块反演方法通过平均弛豫时间仅将地下环境假想为单一孔隙.然而,核磁共振测井及实验室核磁共振[19]技术指出,每一地层中探测到的MRS信号可视为不同孔隙产生的弛豫信号叠加.根据磁共振表面弛豫扩散理论,孔隙内流体的弛豫时间与孔隙大小以及形状密切相关,较小孔隙对应信号的弛豫时间短,反之,较大孔隙对应信号的弛豫时间长[20].由上述分析可知,地面磁共振信号应具有多指数特性,而多指数FID信号可通过方程(10)表述:
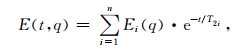
|
(10) |
其中,T2i(i=1,2,…n)表示地下环境中第i类孔隙物质对应的弛豫时间,Ei表示第i类弛豫单元对总MRS信号的贡献.
分析多指数方式描述磁共振信号对获取信号初始振幅的意义.图 2直观给出单指数方式和多指数方式针对含有噪声的FID仿真信号的拟合情况,黑色点即以信噪比以10dB为例的FID信号;空心圆圈为初始振幅值;黑色及灰色实线分别为采用单指数拟合及多指数拟合FID信号的结果.由图可见,单指数拟合后得到的信号初始振幅低于模型设定值;而多指数方式获得的初始振幅与模型设定值吻合.从趋势而言,采用多指数拟合能够更好的逼近FID信号整个衰减过程.

|
图 2 磁共振FID仿真信号的单指数和多指数拟合对比 Fig. 2 The comparison of mono-exponential and multi-exponential fitting of FID model data |
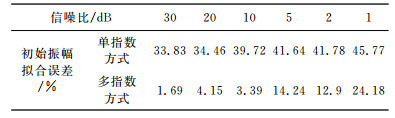
表 1分析了不同信噪比下分别采用单一指数拟合和多指数拟合的初始振幅拟合误差.通过对比可以发现,在不同信噪比下,多指数拟合信号初始振幅的准确度均高于单一指数拟合,尤其在低信噪比(1~2dB)的情况下仍能比较理想的进行初始振幅拟合.初始振幅的大小直接决定了反演的准确性,因此,采用多指数方式描述磁共振信号对反演解释将具有重要意义.
|
|
表 1 不同信噪比下初始振幅拟合误差 Table 1 Initial amplitude fitting error in different SNR |
由前所述,平滑反演和分块反演方法均通过初始振幅-脉冲矩曲线实现地下水垂向分布反演,忽略了大部分弛豫信号,导致各脉冲矩下信息独立,造成较大反演偏差.考虑到核函数的积分特性,即信号在相邻时间相邻脉冲矩下的信息并非完全独立,本文由此提出了分层模式与多指数结合的磁共振全弛豫信号反演方法,能够直接建立地下含水层位置、各层含水量大小及其映射弛豫时间的关系.
2.3.1 弛豫信号多指数的正演推导为实现弛豫信号的反演方法,需要重新推导磁共振弛豫信号的正演方程,建立弛豫信号与地下含水量之间的关系.公式为
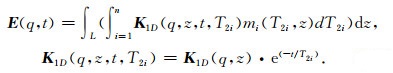
|
(11) |
其中,mi(T2i,z)>0,i=1,2,…,n代表地层z处不同弛豫时间T2i对应的含水量大小.K1D(q,z,t,T2i)是本文建立的弛豫信号的一维核函数矩阵,宏观上说,新核函数通过不同弛豫时间T2的e指数因子刻画了在多指数前提下脉冲矩随着时间变化的磁共振响应.根据弛豫时间与含水地层对应关系[21],确定30ms<T2<1000ms,在此范围内选取合适的T2谱分布作为先验信息.
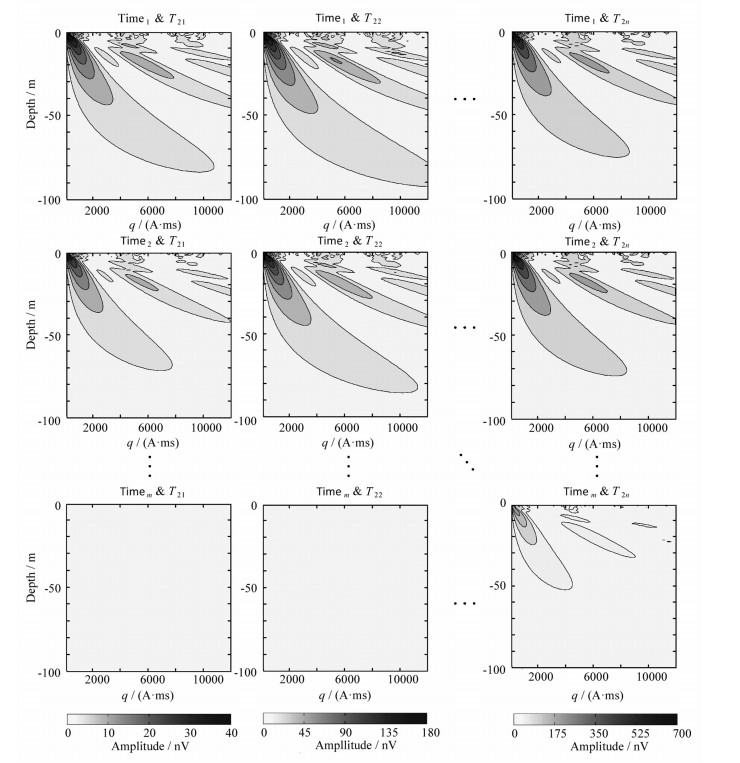
为使该正演过程更加清晰,笔者在图 3绘制了新的核函数,横轴代表弛豫时间T2,纵轴代表信号时间t.m行n列的子核函数矩阵能够精细描述出不同信号采集时间下、不同弛豫时间T2对应的随深度及脉冲矩变化的MRS响应.图 3中可见,随着时间增加,同一T2下对MRS的响应逐渐衰减,小T2对应的响应衰减快,大T2对应的响应衰减慢,这与本文2.2中的磁共振表面弛豫扩散理论吻合.
|
图 3 分层多指数一维核函数图 Fig. 3 Layered multi-exponential one dimensional kernel matrix |
将方程(11)离散化得到多指数下磁共振FID信号与含水量的关系,用矩阵形式表示为
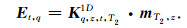
|
(12) |
磁共振分层多指数反演之目的是要获得从地表至最大探测深度的地下水分布情况及赋存状态,即求解方程(12)中的mT2,z,对该矩阵的求解过程也是决定反演收敛速度的关键.由于采用全弛豫信号进行反演,涉及的数据量庞大,同时为避免光滑连续模型中出现的迭代缓慢及水层分界模糊现象,文中采取了分层控制方式突出含水边界,经有限步的计算就可以得到精确解.
将待反演的含水层个数设为控制量,分层数为k.若地下实际存在的含水层个数为θ,则地层分层数至少为2θ+1.仅当含水层个数小于激发脉冲矩个数时能获取较好的反演效果,固而确定k的取值范围为2θ+1≤k<g,g代表激发脉冲矩个数.对含水层层顶深度zt和层底深度zb求解,就能够确定含水层的位置及厚度,它们是构成本文分层反演的核心,方程(13)给出了分层多指数反演中含水量与深度及弛豫时间的关系:
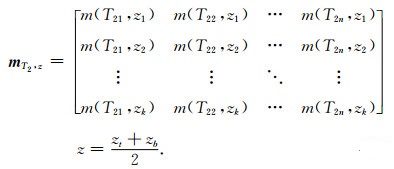
|
(13) |
在方程(12)中,反演参数表现为mT2,z=[mz1T21 ,…,m zkT21,mz1T22 ,…,mzkT2n ]T,这是n×k维列向量,磁共振全弛豫信号数据Et,q=[Eq1t1 ,…,Eqgt1 ,Eq1t2 ,…,Eqgt p ]T是p×g维列向量,核函数是(n×k)×(p×g)矩阵.
由于方程(12)是不适定的,需通过其近似解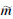
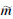
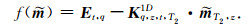
|
(14) |
人们求解含水量反演这类非线性规划问题的方法主要有拟牛顿法和共轭梯度法等.但这些方法过于依赖初值选取,有时还会限于局部极值,无法找到全局极值.鉴于传统方法的缺点,我们引入空间信赖域算法[21-22],这是现代应用较广泛的地球物理反演方法,基本思想在于:通过一系列信赖域子问题的最优值逼近最优化问题的解.该方法稳定的数值性能,适合于求解病态最优化问题,并具备全局收敛性.对于无约束或等式约束的优化问题,该方法已被证实是可靠而强适的.笔者通过构造信赖域子问题,得到不等式约束优化问题的信赖域算法.
建立目标函数的最小二乘形式,方程为
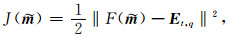
|
(15) |
其中,F(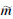
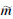
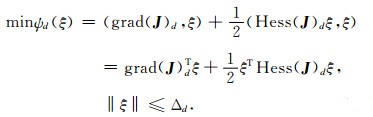
|
(16) |
其中,grad(J)d和Hess(J)d分别代表泛函J在迭代点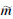

|
(17) |
其中,F′(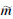
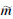
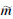
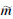
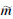
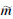
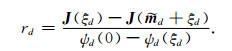
|
(18) |
接受后,获得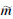
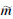
(1)不等式约束的施加
为了减小解的范围,根据反演变量的物理意义对其进行不等式约束.zt与zb代表地下深度,定义地表深度为零,则有zt≤0,zb≤0.含水量指单位体积内含水体积占总体积的百分比,确定一个宽泛的取值范围,则有第j层含水层弛豫时间为T2i对应的含水量m(T2i,zj)>0,(i=1,…,n;j=1,…,k),第j层含水层总含水量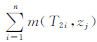

|
(19) |
将不等式约束施加于反演方程能够有效的约束信赖域空间,提高反演效率.
(2)正则化参数的确定
正则化方法是解决反演问题多解性的有效方法之一,通过用一个近似的适定问题代替来减少解的不稳定性.正则化参数的选取影响到正则解对于准确解的逼近程度.而与传统反演方法不同,信赖域算法具有自动调节正则化参数的功能,克服了常用正则化方法中通过Morozov后验偏差等准则求取参数的困难.
本文正则参数α的确定以使目标函数(16)在迭代过程中下降为原则,为此给α一个非零初值使得
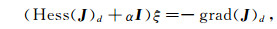
|
(20) |
其中,I为单位矩阵.为保证算法顺利进行,调节正则化参数α使Hess(J)d+αI是正定的,则ξ唯一的由方程(21)决定,有
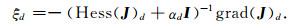
|
(21) |
然后判断ξd是否落在信赖域半径Δd内,满足‖ξd‖≤Δd则接受该点,并转入下一步迭代,否则按αd+1=αd·γ(γ>1)调节参数,使每次迭代的目标函数为一单调下降序列,直至(15)式迭代收敛到一个稳定数值解.
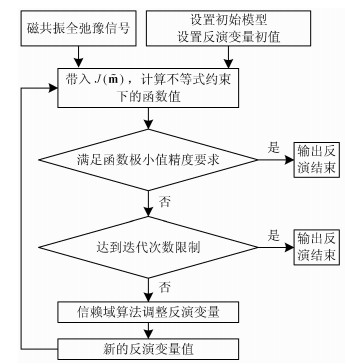
图 4为分层多指数反演流程图.
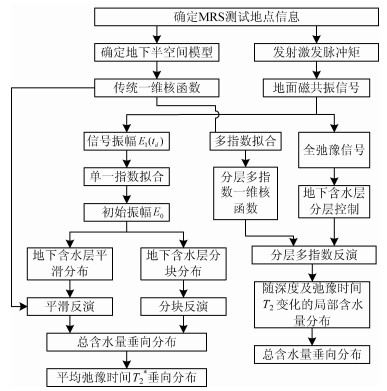
图 5是本文归纳的平滑反演、分块反演和分层多指数反演的总体流程框图.
|
图 4 分层多指数反演流程图 Fig. 4 Flow chart of layered mult-exponential inversion |
|
图 5 反演方法流程框图 Fig. 5 Schemes of inversion methods |
构造单一弛豫时间T2多含水层模型,分别设置含水层弛豫时间及含水量,比对平滑、分块、分层多指数三种方法反演效果.
模型数据是在如下条件下通过正演计算获得:
(1)边长100 m的单匝方形线圈,采用收发共线方式;
(2)假设地下为均匀半空间,电阻率为500μm.地磁场强度B0=46970nT,地磁倾角60°;
(3)拉莫尔频率为2000Hz,激发脉冲矩从0.4As到10As分为20次激发地下0m到100m;
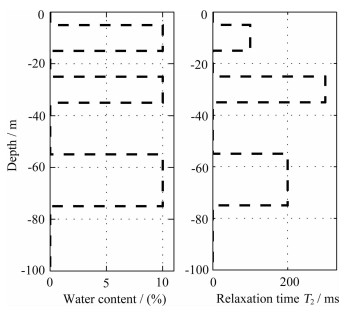
(4)假设地下存在三个含水层(图 6),第一层设置于地下浅层5m至15m,含水量为10%,弛豫时间T2为100ms;第二层设置于地下中层25m到35m,含水量为10%,弛豫时间T2为300 ms;第三层设置于地下深层55m到75m,含水量为10%,弛豫时间T2为200ms;
|
图 6 模型一 Fig. 6 Model one |
(5)由于磁共振方法采集信号水平在纳伏级,易受到噪声的干扰,导致反演精度下降.因此,为使仿真结果接近实际并验证该方法的适用性,在正演模型中加入5%Guass白噪声.设置反演地层个数k=10;初始正则化参数α=100.
图 7给出了模型一的反演结果.(a)为含噪磁共振数据,蓝色实线为不同脉冲矩下的信号衰减曲线,红色圈为不同脉冲矩下接收时刻信号的幅值E1(td).图(b)、(c)中左图分别为平滑反演和分块反演得到的含水量垂向分布,右图为平均弛豫时间T2*垂向分布,红色虚线为模型值,蓝色实线为反演值.(d)中左图为分层多指数反演得到的地下含水量分布,横轴代表弛豫时间T2,纵轴代表深度,颜色代表含水量;右图为总含水量结果,红色虚线为模型值,蓝色实线为反演值.

|
图 7 模型一数据反演结果 (a)模型一数据;(b)平滑反演结果;(C)分块反演结果;(d)分层多指数反演结果. Fig. 7 Inversion results of model one data (a) Data set of model one; (b) Resutt of smooth inversion; (c) Resutt of block inversion; (d) Resutt of layered multi-exponential inversion. |
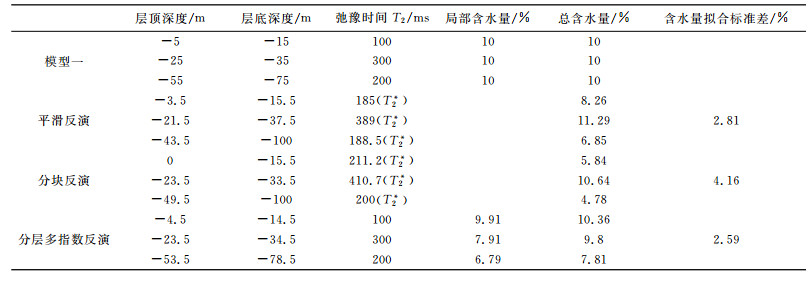
表 2列出了采用平滑、分块以及分层多指数三种反演方法处理模型一数据的反演结果,对比了反演含水层的层顶深度、层底深度、含水量及弛豫时间,并对总含水量的拟合情况进行了误差分析.
|
|
表 2 模型一数据反演结果 Table 2 Inversion results of model one |
通过图 7及表 2可以得出结论:平滑反演和分块反演能够得到地下含水量及平均弛豫时间的垂向分布,但由于方法的固有缺陷,无法定位深层含水量的准确位置,总含水量拟合数值偏小,误差较大.分层多指数反演能够得到地下随深度及弛豫时间T2的含水量分布情况.同时它精确区分了浅层、中层、深层的含水构造,与模型设置基本一致,总含水量反演结果准确,拟合误差仅为2.59%.
3.2 模型实验二构造多弛豫时间T2含水层模型.
模型数据是在如下条件下通过正演计算获得:
(1)边长为100 m的单匝方形线圈,采用收发共线方式;
(2)假设地下为均匀半空间,电阻率为500μm.地磁场强度B0=46970nT,地磁倾角为60°;
(3)拉莫尔频率为2000Hz,激发脉冲矩从0.4As到10As分为20次激发地下0m到100m;
(4)假设地下存在两层含水层(图 8),第一层设置于地下浅层20m至40 m,含有两种弛豫时间成分,T21为100ms,对应含水量为5%,T22为400ms,对应含水量为5%;第二层设置于地下深层60m至80m,含有两种弛豫时间成分,T21为200 ms,对应含水量为5%,T22为600ms,对应含水量为5%;

|
图 8 模型二 Fig. 8 Model two |
(5)模型中加入5% Guass白噪声.设置反演地层个数k=8,初始正则化参数α=100.
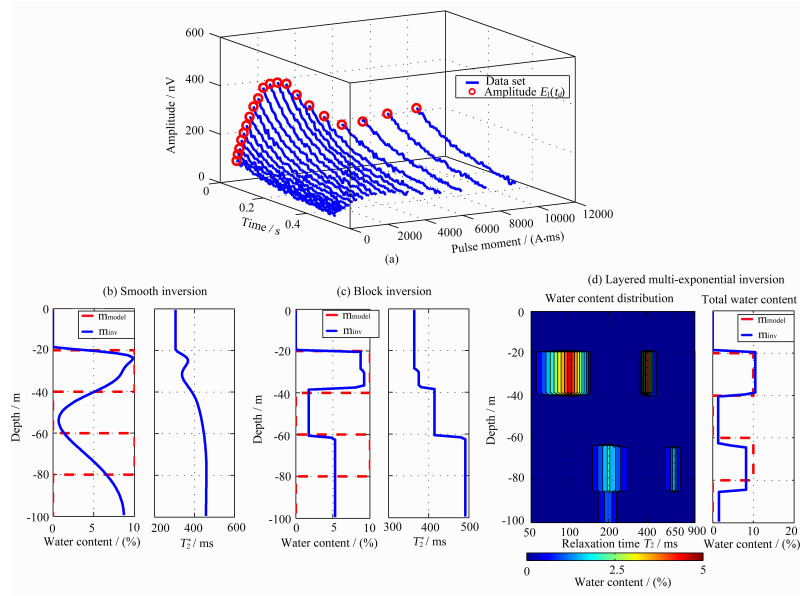
图 9和表 3给出了三种方法处理模型二数据的反演结果.结论如下:平滑反演和分块反演无法准确获得深部含水层位置信息,并且仅能获得平均弛豫时间T2*,无法区分同一含水层的不同弛豫时间分布,含水量拟合误差分别达到4.79%及3.59%.而分层多指数反演能精确实现浅层、深层含水定位,与模型基本相符.同时,在浅层和深层区分出给出不同弛豫时间T2及其映射的含水量分布情况,含水量拟合误差仅为2.86%.表 3中给出最大局部含水量所对应的弛豫时间T2.此外,图 9(d)中右图所示的总含水量则代表每一含水层多个弛豫时间所映射的含水量之和,与模型设置吻合.
|
图 9 模型二数据反演结果 (a)模型二数据;(b)平滑反演结果;(c)分块反演结果;(d)分层多指数反演结果. Fig. 9 Inversion results of model two data (a) Data set of model two; (b) Resutt of smooth inversion; (c) Resutt of block inversion; (d) Resutt of layered multi-exponential inversion. |
|
|
表 3 模型二数据反演结果 Table 3 Inversion results of model two |
需要指出的是,随着探测深度的增加,磁共振响应的分辨率逐渐降低,T2反演精度下降,向相邻的T2值均匀扩散,这是导致深层两个弛豫时间映射含水量偏小的本质原因.但从总含水量的数值而言,分层多指数反演更接近于模型,显著优于传统反演方法.
4 野外数据实例经模型数据验证分层多指数方法后,本文对野外实测MRS数据进行反演处理,证明其适用性.
研究组利用吉林大学自主研发的JL-MRS磁共振地下水探测仪于白城市镇赉县四方坨子嫩江岸边进行了150 m地下水探测试验.测试点地磁场55936nT,采用边长150 m方形线圈,激发频率为2383Hz.钻探结果表明含水层见于井深3m到21m、63m到106m和126m到148m处,含水层厚度共83m,为孔隙承压水,静止水位4 m,当水位下降至7m时的涌水量为320t/h.
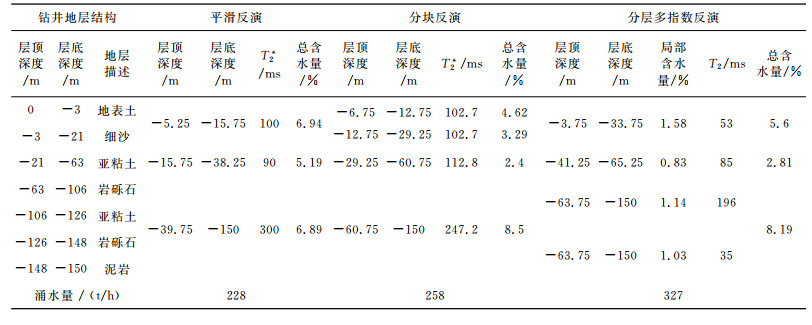
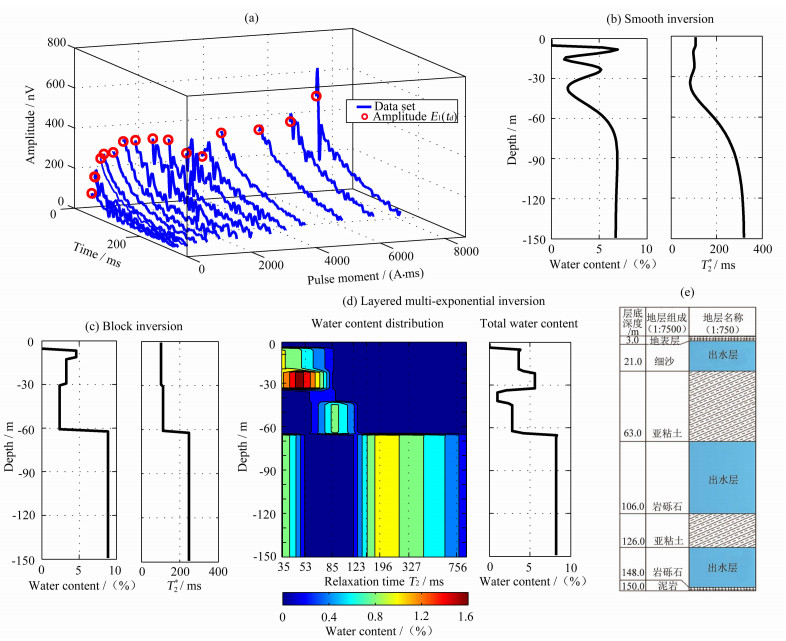
图 10a为实测数据,平均信噪比达34.68dB(相当于信号中仅含有1.85%的噪声,在核磁共振反演中,信噪比高于6.02 dB数据即为真实可信[23]).图 10(b-d)是分别采用平滑、分块和分层多指数方法对数据进行反演的结果,图 10e为钻井成图.表 4给出了白城测点钻井地层结构与三种反演方法的结果对比情况.平滑反演得到地下存在两层含水层,浅层位于地下5.25 m至38.25 m,深层存在含水层但无法确定其具体位置,其平均弛豫时间T2*分布平缓过渡,无法与含水层准确对应.分块反演显示地下主要存在两层含水层,浅层位于地下6.75m至29.25 m,同样无法准确体现深层含水层的位置,与平滑反演相较,T2*有明确划分,然而深层含水层仅有较大弛豫时间247.2 ms的反演解释结果与野外实际地层情况有一定偏差.上述两种方法反演的含水层均为连续变化,未见相对隔水层出现.分层多指数方法的初始正则化参数α=100,反演设置地层个数k=10(参数优化后,E0-q曲线拟合误差最小).结果显示地下主要存在两个含水层,浅层位于地下3.75m至33.75m,从弛豫时间上看地表土对应的T2为53ms;隔水构造出现在33.75m与41.25m之间,该隔水构造对应右图所示的较小的含水量分布;中间层亚粘土地层位于地下41.25m至65.25m,对应的弛豫时间T2为85 ms比理论值略大,因实际探测中,亚粘土属于束缚水构造(一般认为磁共振探测为自由水),反演拟合易造成偏差,而成为上下两个含水层弛豫时间值的过渡.深层含水层层顶位置反演准确,从弛豫时间上看,地下63.75m至150m主要存在两个弛豫时间成分,分别是35ms和196 ms,能够对应于钻井结果63 m到148 m的岩砾石结构与亚粘土.随着深度的增加,激发场逐渐减弱,导致了磁共振响应分辨率随着深度的增加而逐渐降低,使得分层多指数方法亦不能明确的给出第三层出水层,但其弛豫时间的分布差异提示在主要含水层中或有隔水介质出现.
|
图 10 白城测点数据反演结果 (a)白城测点数据;(b)平滑反演结果;(c)分块反演结果;(d)分层多指数反演结果;(e)测点钻探成井图. Fig. 10 Inversion results of Baicheng test (a) Dataset of Baicheng test; (b) Smooth inversion result; (c) Block inversion result; (d) Layered multi-exponential inversion result; (e) Drilling result. |
|
|
表 4 白城四方驼子钻井结果与反演结果对比 Table 4 The comparison of drilling result and inversion results at BaichengSifangtuozi |
在实测数据处理中,分层多指数反演在含水层的位置上与钻井结果一致性最好,且能够通过弛豫时间T2分布来明确地下岩石结构.分别利用三种反演方法进行涌水量评估,发现平滑反演和分块反演计算的涌水量值偏小,而分层多指数反演得到该测点的涌水量约为327t/h,与钻井结果320t/h基本相符,说明了分层多指数方式能够准确评价地下水赋存情况.
5 结论通过对比平滑反演、分块反演和分层多指数反演方法处理模型数据及野外实测数据算例,本文得出如下结论:
(1)分层多指数反演采用多指数方式来拟合FID信号,摒弃了平滑与分块反演中参数提取环节,降低了传统单一指数拟合引入的误差对反演结果的影响;将弛豫信号所有数据一次性带入反演计算,建立起相邻脉冲矩之间及相邻时间下信号的相互关系,提高了反演结果的准确性与稳定性.
(2)与平滑与分块反演得到的含水量垂向分布相比较,分层多指数反演能够得到随深度及弛豫时间T2变化的含水量分布情况,更加直观的反映出地下水的赋存状态,适用于多岩性解释的复杂地质环境.
(3)分层多指数反演采用设定地下分层个数的方式,以及不等式约束下的空间信赖域算法,缩短了反演所需时间,使得各含水层之间分界明显,不仅有助于实际应用中准确判断含水层所处的位置,还避免了预先设置复杂反演控制参数导致的人为结果偏差.
本文突破了传统地面MRS技术仅局限于平均孔隙度解释的瓶颈,提供了MRS在复杂地质构造下进行全数据反演解释的新思路,而随着多通道[24] MRS仪器的问世,该反演方法可进行深入研究,从而拓展应用到二维全数据的反演解释之中.
| [1] | Legchenko A, Valla P. A review of the basic principles for proton magnetic resonance sounding measurements. Journal of Applied Geophysics , 2002, 50(1-2): 3-19. DOI:10.1016/S0926-9851(02)00127-1 |
| [2] | Legchenko A, Baltassat J M, Beauce A, et al. Nuclear magnetic resonance as a geophysical tool for hydrogeologists. Journal of Applied Geophysics , 2002, 50(1-2): 21-46. DOI:10.1016/S0926-9851(02)00128-3 |
| [3] | 潘玉玲, 张昌达. 地面核磁共振找水仪理论与方法. 北京: 中国地质大学出版社, 2000 . Pan Y L, Zhang C D. The Theory and Methods of Water Detecting (in Chinese). Beijing: Publishing House of China University of Geosciences, 2000 . |
| [4] | 林君, 段清明, 王应吉, 等. 核磁共振找水仪原理与应用. 北京: 科学出版社, 2011 . Lin J, Duan Q M, Wang Y J, et al. Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Defection and Its Applications (in Chinese). Beijing: Science Press, 2011 . |
| [5] | 张昌达, 潘玉玲. 关于地面核磁共振方法资料岩石物理学解释的一些见解. 工程地球物理学报 , 2006, 3(1): 1–8. Zhang C D, Pan Y L. Some views on petrophysical interpretation of SNMR data. Chinese Journal of Engineering Geophysics (in Chinese) , 2006, 3(1): 1-8. DOI:10.1088/1742-2132/3/1/001 |
| [6] | Legchenko A V, Shushakov O A. Inversion of surface NMR data. Geophysics , 1998, 63(1): 75-84. DOI:10.1190/1.1444329 |
| [7] | Mohnke O, Yaramanci U. Smooth and block inversion of surface NMR amplitudes and decay times using simulated annealing. Journal of Applied Geophysics , 2002, 50(1-2): 163-177. DOI:10.1016/S0926-9851(02)00137-4 |
| [8] | 翁爱华, 王雪秋, 刘国兴, 等. 导电性影响的地面核磁共振反演. 地球物理学报 , 2007, 50(3): 890–896. Weng A H, Wang X Q, Liu G X, et al. Nonlinear inversion of surface nuclear magnetic resonance over electrically conductive medium. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 890-896. |
| [9] | 戴苗, 胡祥云, 吴海波, 等. 地面核磁共振找水反演. 地球物理学报 , 2009, 52(10): 2676–2682. Dai M, Hu X Y, Wu H B, et al. Inversion of surface nuclear magnetic resonance. Chinese J. Geophys. (in Chinese) , 2009, 52(10): 2676-2682. |
| [10] | Mohnke O, Yaramanci U. Forward modeling and inversion of MRS relaxation signals using multi-exponential decomposition. Near Surface Geophysics , 2005, 3(3): 165-185. |
| [11] | Yaramanci U, Müller-Petke M. Surface unclear magnetic resonance-a unique tool for hydrogeophysics. The Leading Edge , 2009, 28(10): 1240-1247. DOI:10.1190/1.3249781 |
| [12] | 孙淑琴, 赵义平, 林君, 等. 用地面核磁共振方法评估含水层涌水量的实例. 地球物理学进展 , 2008, 23(4): 1317–1321. Sun S Q, Zhao Y P, Lin J, et al. Example of evaluating groundwater-saturated layers yield capacity based on the surface NMR method. Progress in Geophys. (in Chinese) , 2008, 23(4): 1317-1321. |
| [13] | Ryom N M, Hagensen T F, Chalikakis K, et al. Comparison of transmissivities from MRS and pumping tests in Denmark. Near Surface Geophysics , 2011, 9(2): 211-223. |
| [14] | Braun M, Hertrich M, Yaramanci U. Complex inversion of surface-NMR signals-extending the limits of model resolution. 17th EEGS symposium on the application of Geophysics to Engineering and environmental problems. Extended Abstracts, 2004: 856-867. |
| [15] | Weichmann P, Lavely E, Ritzwoller M. Theory of surface nuclear magnetic resonance with applications to geophysical imaging problems. Physical Review E , 2000, 62(1): 1290-1312. DOI:10.1103/PhysRevE.62.1290 |
| [16] | Müller M, Hertrich M, Yaramanci U. Analysis of magnetic resonance sounding kernels concerning large scale applications using SVD. Proc. SAGEEP, EEGS. 2006, 19(1): 595-603. |
| [17] | 唐隆基, 李文, 邓阳生. 关于解地球物理中病态方程的若干问题. 地球物理学报 , 1995, 38(1): 105–114. Tang L J, Li W, Deng Y S. Some aspects for solving ill-posed equation in geophysics. Chinese J. Geophys. (in Chinese) , 1995, 38(1): 105-114. |
| [18] | 张文权, 翁爱华. 地面核磁共振正则化反演方法研究. 吉林大学学报(地球科学版) , 2007, 37(4): 809–813. Zhang W Q, Weng A H. On regularization inversion method of surface nuclear magnetic resonance data. Journal of Jilin University (Earth Science Edition). (in Chinese) , 2007, 37(4): 809-813. |
| [19] | Mohnke O, Yaramanci U. Pore size distributions and hydraulic conductivities of rocks derived from Magnetic Resonance Sounding relaxation data using multi-exponential decay time inversion. Journal of Applied Geophysics , 2008, 66(3-4): 73-81. DOI:10.1016/j.jappgeo.2008.05.002 |
| [20] | Schiroc M, Legchenko A, Creer G. A new direct non-invasive groundwater detection technology for Australia. Exploration Geophysics , 1991, 22(2): 333-338. DOI:10.1071/EG991333 |
| [21] | 曾齐, 师学明, 武永胜, 等. 一维大地电磁信赖域反演法研究. 地球物理学进展 , 2011, 26(3): 885–893. Zeng Q, Shi X M, Wu Y S, et al. A study of one-dimensional magnetotelluric sounding inversion using the trust region algorithm. Progress in Geophys. (in Chinese) , 2011, 26(3): 885-893. |
| [22] | 田玥, 陈晓非. 利用拟牛顿法和信赖域法联合反演震中分布与一维速度结构. 地球物理学报 , 2006, 49(3): 845–854. Tian Y, Chen X F. Simultaneous inversion of hypocenters and velocity using the quasi-Newton method and trust region method. Chinese J. Geophys. (in Chinese) , 2006, 49(3): 845-854. |
| [23] | Legchenko A. MRS measurements and inversion in presence of EM noise. Boletín Geológico y Minero , 118(3): 489-508. |
| [24] | Walsh D. Multi-channel surface NMR instrumentation and software for 1D/2D groundwater investigations. Journal of Applied Geophysics , 2008, 66(3-4): 140-150. DOI:10.1016/j.jappgeo.2008.03.006 |
 2013, Vol. 56
2013, Vol. 56