有效压力方程(peff=pc-αpp)是研究岩石渗透率和孔隙度等物性参数随孔隙压变化的重要基础[1].研究者一般把有效压力看成是线性的,即有效压力方程中的系数α是常数[2-5].α=1.0时对应的是经典的Terzaghi有效压力方程[5].研究者可根据Terzaghi有效压力方程把变围压实验结果转换成孔隙压对岩石物性参数影响的结果[1].不少研究者利用Terzaghi线性有效压力方程开展了大量的工作,发现岩石渗透率随围压的变化显著[6-8];高渗岩石孔隙度随围压的变化相对较大,而低渗岩石孔隙体积太小以至实验误差相对围压对孔隙度的影响更显著,于是低渗岩石的孔隙度常借助与渗透率的关系计算得到[7].在Robin[2]进一步定义有效压力概念,并认为非线性有效压力(α不是常数)不会满足其给出的有效压力定义后,很多研究者认为没有应用意义的非线性有效压力.因此,也就难以见到用非线性有效压力来研究岩石物性随孔隙压变化规律相关文献.然而用线性有效压力研究岩石物性随孔隙压的变化常常与实际物性随孔隙压的变化规律不一样,因此促使一些研究人员[9-13]不断地探索有实际应用意义的非线性有效压力.研究有效压力的关键是确定有效压力系数α,基于实验测试获取有效压力是一种有效的方法.至今关于非线性有效压力的研究很少,文献报道的关于α的实验分析方法主要有微分法[10, 14]、交绘图法[10, 15]和响应面法[12-13].
最初的微分法是Kranz等[14]根据实验渗透率与围压和孔隙压的差值满足某一函数关系,建立了渗透率与围压和孔隙压的差值间的微分方程和α的计算公式.交绘图法是Walsh[15]用渗透率公式k1/3=Alog(pp)+B(A、B是拟合系数)拟合不同围压下渗透率与孔隙压的实验数据,在[pp,pc]平面图上绘制渗透率等值线,等值线的斜率即为有效压力系数.之后,Bernabé[10]通过建立渗透率与围压和孔隙压的微分方程,并假定在某点很小的范围内α为常数,推导得α=-(δk/δpp)/(δk/δpc);改变相同大小孔隙压或者围压,测渗透率的变化量,那么α=-δkp/δkc;或者改变孔隙压δpp和围压δpc使得渗透率变化值相等,那么α=-δpc/δpp,这与[pp,pc]平面图上渗透率等值线斜率相等.同时,Bernabé[10]通过修正Walsh公式[15]为kn=Alog(pc)+B(0<n≤1/3,n是与孔隙压相关的系数)完善了交绘图法.Bernabé[10]用这两种方法分析了裂缝花岗岩渗透率实验数据[10]和Todd的花岗岩纵波速度实验数据[9],得到α随围压的增加而减小,随孔隙压的增加而增加.然而每个实验点测试质量对微分法计算的α影响较大;随围压的增加,交绘图法对渗透率的拟合误差增加,α的计算误差也增加.此后,Warpinski和Teufel[12]用响应面方法分别获取了碳酸盐岩和低渗砂岩整个测试压力范围内渗透率和体应变与围压和孔隙压的函数关系.他们用α=-(δk/δpp)/(δk/δpc)计算得到碳酸盐岩α变化范围较小,有效压力可视为线性的;而低渗砂岩α变化范围较大(0.4~1.1),有效压力非线性明显.响应面法的优点在于最大限度地保证了α沿测点路径上变化的连续性,在整个实验测试范围内,基本上不会因测试路径上数据质量问题而造成α上下波动.Li等[13]也采用响应面法分析了含微裂缝低渗砂岩的有效压力实验数据,发现每块岩样的α随围压和孔隙压的变化而变化(0~1.23),有效压力表现出明显的非线性特征.同时,Li等[13]还证明了部分岩样在不同孔隙压循环围压下有效压力与渗透率几乎完全重合在一起,初步论证得到了有应用意义的非线性有效压力.
上述三种方法本质都是基于α=-(δk/δpp)/(δk/δpc)来计算有效压力系数.对比分析Bernabé在[pp,pc]平面上的渗透率等值曲线形态[11]可以发现,这三种方法获取的α等于[pp,pc]平面图上对应压力点处渗透率等值线切线的斜率.Bernabé称之为切线有效压力系数αt,对应的有效压力是切线有效压力.对非线性有效压力的不断探讨,使人们进一步意识到非线性有效压力的客观存在.按照[pp,pc]渗透率等值线的变化形态分析,只有当渗透率等值线是直线时切线有效压力才有实际意义,这是Li等[13]部分岩样各个测点的有效压力与渗透率重合很好的原因.如果按照Bernabé[11]猜测的渗透率等值线有时是一向上凹的曲线,那么现有方法得到的有效压力此时不满足有效压力的基本定义.本文通过引入割线有效压力系数αs并计算割线有效压力,得到了满足Robin[2]定义的有效压力概念且有实际应用价值的非线性有效压力.
2 非线性有效压力及计算步骤为了更好地理解非线性有效压力,首先回顾一下Robin[2]关于有效压力的基本概念.Robin指出,岩石的各种性质会在围压pc和孔隙压pp的作用下发生变化.因此,岩石的性质是围压和孔隙压的函数.如果所研究的对象是岩石的渗透率,渗透率k可以表示为围压和孔隙压的函数,那么有:
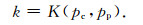
|
(1) |
根据Robin[2]的观点,当孔隙压等于零时,式(1)可以表示为:
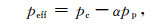
|
(2) |
如果孔隙压不为零,那么就定义一个有效压力peff,其对岩石渗透性的作用与孔隙压为零时围压对岩石渗透性作用产生的影响相同,也和某一围压和孔隙压共同对岩石的渗透性作用的效果一样,这个压力peff称为渗透率有效压力,通常简称为有效压力.从有效压力的定义可以看出,任意围压和孔隙压的组合,只要它们的有效压力相等,那么岩石物性也相同.若不满足这一条,那么得到的有效压力就没有实际的应用意义.
有效压力可表示为pc和pp的函数.如有效压力方程是线性的,那么有:

|
(3) |
式中有效压力系数α是常数.如果有效压力方程是非线性的,得到下面的表达式[10-11, 13]:

|
(4) |
此时有效压力系数是围压和孔隙压的函数.Robin认为式(3)符合有效压力的概念,原因是α有时取常数时,用有效压力公式(3)计算得到不同定孔隙压循环围压,或定围压循环孔隙压测定的岩石渗透率与有效压力测点基本叠和在一起[4, 16].说明不同围压和孔隙压下,只要有效压力相同,岩石的渗透率大小是一样的.这样就可以通过有效压力方程(3),把两参数(围压和孔隙压)与渗透率的关系,转换成有应用意义的单参数有效压力和渗透率的关系.由于当时没有提出计算非线性有效压力的方法,无法论证得到有实际应用意义的有效压力[2].
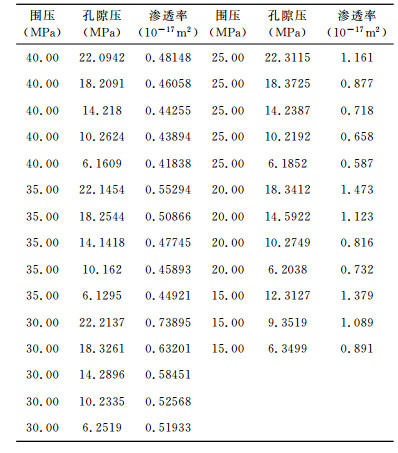
Bernabé[11]根据花岗岩渗透率有效压力实验[10]和花岗岩纵波速度有效压力实验[9]的研究结果,在[pp,pc]平面直角坐标系中绘制了渗透率等值线(图 1).Bernabé[11]认为等值线上某点的α=-δpc/δpp.因此,在孔隙压不变的条件下,B点的α>C点的α;同样B点的α<B′点的α.即有效压力系数α随围压的增加而减小,随孔隙压的增加而增加.Bernabé[11]并不认为这个有效压力系数αt有什么实际意义.例如,沿图 1中N点的切线方向可以延伸至孔隙压为零的M′点.显然,M′点的围压与N点等值线延伸至孔隙压为零的围压(有效压力)不相同.图 1中N点围压和孔隙压对岩石渗透性的作用效果与M点孔隙压为零时围压对岩石渗透性作用产生的效果一样,M点的围压等于N点的有效压力peff;而M′则因渗透率值与N点的渗透率值不一样,M′点的围压不等于N点的有效压力peff,所以按照Bernabé[10]方法计算的有效压力不满足有效压力的基本概念.同时,M′点的渗透率不等于N点的渗透率,这一差别是造成切线有效压力没有实际应用意义的原因.为了避免其它研究人员的疑惑,Bernabé[11]把αt称为“局部”有效压力系数,计算得到的有效压力称为切线有效压力.

|
图 1 Bernabé[11]猜测在pc和pp等图中渗透率等值线形态. Bernabé认为α随围压的增加而减小,随孔隙压的增加而增加. Fig. 1 Schematic representation of curved iso-k lines conjectured by Bernabé[11] α is believed to decrease with increasing pc and decreasing pp. |
从图 1中连接N点和M点的割线(图中虚线)可以看出,割线连接的M和N点都在渗透率等值线上.因为孔隙压等于零,M点的围压就是M和N点等值线上的有效压力.M和N点的坐标已知,通过建立M和N点的直线方程,并考虑M点的围压(pc)M等于有效压力peff,得到

|
(5) |
令
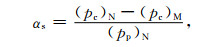
|
(6) |
式中αs称为割线有效压力系数,将式(6)代入式(5),得到
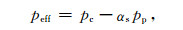
|
(7) |
由式(7)计算得到的有效压力称为割线有效压力.这里不妨讨论一下αt和αs的关系及对应的切线和割线有效压力是否满足有效压力的基本定义:
(1)当等值线是曲线时,αt和αs不相等,切线有效压力不等于割线有效压力.切线有效压力不满足有效压力的定义,而割线有效压力满足有效压力的定义;
(2)当等值线是直线时,αt和αs相等,切线和割线重合.如图 1中的M″和N″所在的直线上,切线和割线重合并都落在M″和N″所在的等值线上,孔隙压等于零,M″点的渗透率与M″和N″所在等值线上的渗透率处处相等,切线有效压力等于割线有效压力,且都满足有效压力的定义;
(3)当所有等值线均为斜率相等的平行直线时,αt和αs相等且为一常数,用这个常数计算得到的有效压力是线性有效压力.这时切线和割线重合,切线有效压力等于割线有效压力,且都满足有效压力的定义.
因此用αs计算得到的有效压力在任何情况下都满足有效压力的定义,而用αt计算得到的有效压力在情况(1)中不满足有效压力的定义.很多情况下αt和αs是相等的,这是Li等[13]部分岩芯的有效压力和渗透率实验数据点在有效压力和渗透率图中重合在一起的原因.
当pp和pc平面图上岩石性质等值线是直线时,αt和αs大小相同,于是可以用Warpinski和Teufel[12]方法计算αs [12-13, 16].其原理是用响应面法处理实验数据,建立渗透率与围压和孔隙压的关系,然后用Bernabé[10]提出的公式α=-(δk/δpp)/(δk/δpc),来计算割线有效压力系数αs.但在计算αs前,并不清楚要计算岩样的αt和αs是否相等,同时前面的分析指出在任何情况下割线有效压力系数αs计算得到的有效压力均满足有效压力的定义,满足有效压力定义的切线有效压力只是割线有效压力的特殊情况.因此,有必要在αt的计算方法基础上,建立计算αs的方法与步骤.具体的步骤如下:
(1)建立渗透率与围压和孔隙压的经验关系.Warpinski和Teufel[12]是最早采用响应面法来研究测试得到的渗透率与围压和孔隙压的关系.这种方法考虑了各种测量变量的随机误差,通过引入转换系数λ,使计算与实验值偏差的联合概率密度趋于极大值,残差平方和最小.因此,最大限度地提高了模型计算值与不同围压和孔隙压下实测值的拟合精度[17-18].郑玲丽等[19]详细地叙述了λ的确定方法,这里不再赘述.研究表明[12-13, 19-22],可以采用下面的经验关系模型建立测试渗透率与围压和孔隙压之间的关系:
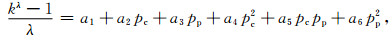
|
(8) |
其中,a1、a2、a3、a4、a5和a6是拟合系数.用回归均方和误差均方的比值F评价拟合效果的好坏,Box[18]认为计算的F值大于等于10倍的查表F值(分布数一般取95%)才能保证拟合效果.
(2)绘制渗透率等值曲线图.可用式(8)计算某个已知围压和孔隙压测点的渗透率.固定这个渗透率值,并给定一孔隙压,这时式(8)中的k、λ和pp都已知,计算式(8)只剩一个未知数pc.通过求解一元二次方程,得到二个解,去除不在实验范围内的pc.每给一个孔隙压pp,就可以计算得到一个pc.将孔隙压和围压计算点连接起来,就可得到这个渗透率在围压和孔隙压图中的等值线.所有的测点采用同样的方法都可以得到每个测点的渗透率等值线.
(3)计算割线有效压力系数αs.可以用式(6)计算αs,但当用气体测量时,压力太低时低渗岩样会产生克氏效应[23],随着压力的降低测量误差会大大增加,加大了问题的分析难度,只能在测试时尽量靠近孔隙压为零的测点.可以采用外推孔隙压来近似确定M点的pc,外推的孔隙压不能太小,Li等[13]认为在测试压力很宽且在测试压力范围内的预测结果是可靠的,而在测试的压力范围外预测的结果可靠性会降低.根据我们的经验,只要实验的孔隙压足够小,实际计算时用式(8)外推孔隙压0.5 MPa,对应的围压pc作为M点的围压,这样就可以用式(6)计算αs.在分析过去的一些实验数据时,有些实验的孔隙压特别大,这时仍可以采用式(8)外推孔隙压至计算得到的pc开始增加时的pc作为M点的围压.计算时要在外推的压力范围内多计算几个点,这样可以对比不同的孔隙压对应的围压,避免出现孔隙压降低围压增加的情况.
(4)有效压力计算.得到每个测点的αs后,就可以根据式(4)计算每个测点的有效压力.如果前面计算得到的αs不是常数且变化范围很大,那么计算得到的有效压力是非线性有效压力;如果前面计算得到的αs是常数或者变化范围很小,那么计算得到的有效压力是线性有效压力.
响应面方法可以建立渗透率和围压与孔隙压的关系式,结合Bernabé[10]提出的公式便可计算αt,同时也可用上面的方法计算αs,再分别计算切线有效压力和割线有效压力.为了区分这两种方法,本文把前者称为“响应面切线有效压力系数法”,而后者称为“响应面割线有效压力系数法”.
3 渗透率测试与有效压力计算试验两块岩芯SM1和SM2分别取自四川省马井气田侏罗纪上统蓬莱镇1564.79m和1497.36m储层.两块岩芯SM1和SM2的渗透率分别是0.238×10-15m2和0.278×10-15m2,孔隙度分别是11.16%和14.26%.铸体薄片观察SM1是极细粒长石岩屑砂岩,SM2是细粒长石岩屑砂岩.两块岩芯孔隙多呈孤立状,连通性差;颗粒之间以线和凹凸接触为主,岩芯中发育有微裂缝.
本文依据李闽等[13, 20]描述的试验步骤用稳态法测试了两块岩芯的渗透率.试验流体介质为氮气,这样可避免液体作介质时粘土的水化作用和岩石与流体的化学反应对试验结果产生影响.试验测试压力分别在定六个围压下(表 1和表 2)降低孔隙压从22 MPa至6 MPa,步长是4 MPa(因为孔隙压不能超过围压,所以当围压为20 MPa和15 MPa时,最大孔隙压分别是18 MPa和12 MPa;同时最低孔隙压大于5 MPa,这可避免滑脱效应对渗透率的影响[13]).试验之前有必要对岩芯进行老化处理,使得岩芯的性质变得更加稳定[12-13, 19-22];也就是岩样在第1次循环围压后,第2次增加围压时各测点渗透率与净应力(围压和孔隙压的差值)和降围压各测点的渗透率与净应力关系点基本上重合在一起.每个压力点至少重复测试五次(包括老化处理),取五次测试得到的渗透率均值作为测点值.测定数据包括岩芯进出口端压力p1、p2,大气压p0,流经岩芯的气体流量Q0和温度T.根据气体渗透率计算公式[24] k=4Q0p0μL/[5πD2(p 2 1-p 2 2)](其中压力单位MPa,流量的单位10-6m3,黏度μ的单位mPa·s-根据压力和温度值查表确定[25],岩芯长度L和直径D的单位10-2m,渗透率单位10-12m2)得到每次测试对应的渗透率.试验结果见表 1和表 2,渗透率值均大于10-18m2,说明稳态法测试渗透率满足研究需要[26].
|
|
表 1 岩芯SM1试验测试数据 Table 1 Experimental data of Sample SM1 |
|
|
表 2 岩芯SM2试验测试数据 Table 2 Experimental data of Sample SM2 |
裂缝的存在是形成非线性有效压力的重要原因,且当岩石有裂缝和孔隙同时存在时会表现出更强的非线性[20].为了有效地验证本文提出的非线性有效压力计算方法,还选取了已发表的10块含裂缝的岩芯计算有效压力.这些样品包括含微裂缝岩屑砂岩2块,分别为S4和S10[13];裂缝Chelmsford花岗岩3块(Chelmsford G、Chelmsford R、Chelmsford H)和裂缝Barre花岗岩1块[10];人造裂缝Barre花岗岩4块[14],其中裂缝面抛光岩芯1块(Barre P),600目砂纸磨裂缝面岩芯1块(Barre 600),120目砂纸磨裂缝面岩芯1块(Barre 120),张力断裂缝岩芯1块(Barre T).这些研究测试时采用了2种测试方式,其中采用定几个围压循环孔隙压测试渗透率的岩芯有S10、Barre P、Barre 600、Barre 120和Barre T,采用定孔隙压循环围压测试的岩芯有S4、Chelmsford G、Chelmsford R和Chelmsford H.
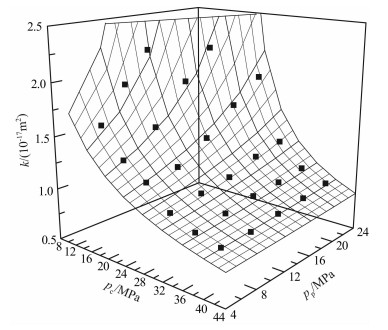
根据响应面方法建立渗透率与围压和孔隙压的关系,计算得到的F值(最小值是15.92)均大于10倍的F查表值(最大值是1.48),拟合满足精度的要求[18],从图 2也可直观地看出拟合效果很好.把渗透率等值线绘制在围压和孔隙压图中,并将所有岩芯测试点标注在围压和孔隙压图中(图 3-图 6中的圆心实点).按照前面介绍的方法计算各个测点的αs,为了比较切线和割线有效压力,这里采用公式(9)计算αt [12-13, 20]:
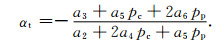
|
(9) |
|
图 2 岩样SM1 k-pc-pp响应面 实心黑点表示实测点,而实线是理论预测值. Fig. 2 Response surface about k-pc-pp of Sample SM1 Solid black dots represent the measured points and the solid line is the theoretical predicted values |
|
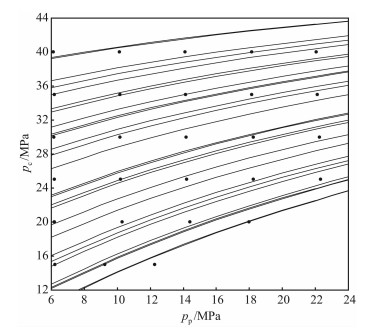
图 6 岩样SM1渗透率等值线 Fig. 6 Iso-k lines of Sandstone SM1 |
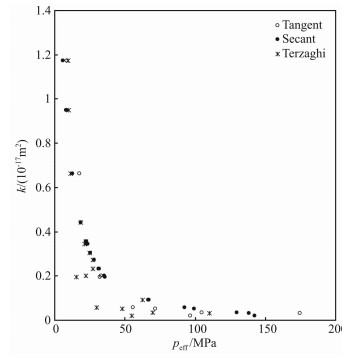
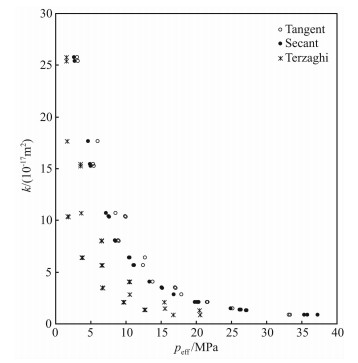
计算得到各个测点的切线和割线有效压力系数后,用式(4)计算各个测试点的切线和割线有效压力,同时还用经典的Terzaghi有效压力方程[5]计算了Terzaghi有效压力.将Terzaghi有效压力方程、响应面切线有效压力系数法和响应面割线有效压力系数法计算得到各个测点的有效压力与渗透率的关系绘制在有效压力和渗透率图中(图 7-图 10).从这些图中看出,Terzaghi有效压力方程得到的各个测点的有效压力与渗透率的关系点分散明显,而切线有效压力和割线有效压力与渗透率的关系点分散程度低很多(图 7-图 10);切线有效压力与渗透率的分散点多于割线有效压力与渗透率的分散点,在图 10中这一现象更为明显,割线有效压力比响应面切线有效压力与渗透率之间表现出了更好的一一对应关系.
|
图 7 Barre 600花岗岩[14]渗透率与有效压力关系 Fig. 7 The relationship between permeability and effective pressure of Granite Barre 600[14] |

|
图 8 Chelmsford H花岗岩[10]渗透率与有效压力关系 Fig. 8 The relationship between permeability and effective pressure of Granite Chelmsford H[10] |

|
图 9 Barre花岗岩[10]渗透率与有效压力关系 Fig. 9 The relationship between permeability and effective pressure of Granite Barre[10] |
|
图 10 S4砂岩[13]渗透率与有效压力关系 Fig. 10 The relationship between permeability and effective pressure of Sandstone S4[13] |
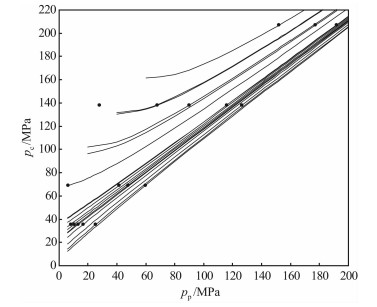
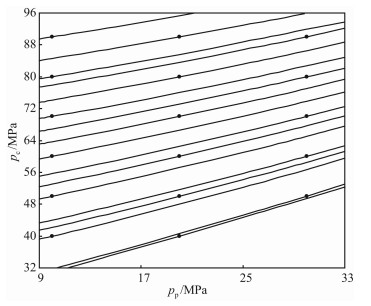
图 3-图 6等值线图表现出四种特征:(1)一部分等值线是直线,另一部分等值线在孔隙压变小时是向上弯曲曲线(图 3);(2)等值线是直线,但相互不平行(图 4);(3)等值线基本上可以看成是相互平行的直线(图 5);(4)等值线在孔隙压变小时是向下弯曲的曲线(图 6).
等值线特征属于(4)的岩样只有SM1(图 6).这块岩样与Bernabé[11]推测的渗透率等值线的形态不一样,也就是不应该出现向下弯曲的曲线;或者说在孔隙压变小时,无论是αs或αt,都应该向小的方向变化.可计算得到SM1岩样在围压15 MPa下的三个孔隙压测点的αs范围在0.908~0.919;围压20 MPa的四个孔隙压测点αs的范围在0.808~0.822之间,曲线朝孔隙压降低的方向向下弯曲变得相对明显,孔隙压变小时αt和αs增加,αt和αs的变化规律也和Bernabé[11]推测的结果不一样.从得到的数值可以看出,尽管存在这种变化,但变化范围微乎其微,仍可以当成常数.此外,从选取的12块岩芯的等值线图看,渗透率等值线都没有出现类似(4)这种特征,可以认为这种特征的出现是由于实验误差造成的.因此,实际只存在类似(1)、(2)和(3)这三种形态等值线图.
图 3和Bernabé[11]推测的渗透率等值线的特征完全一样,有这种曲线特征的岩样有SM2、S4、S10、BarreP花岗岩、Barre600花岗岩、Barre120花岗岩和BarreT花岗岩,共计7块岩样.Bernabé[11]并没有给出类似图 4(岩芯Chelmsford H花岗岩)和图 5(Barre花岗岩、Chelmsford G和Chelmsford R)这两种等值线变化形态.图 4中的等值线基本上都是直线,等值线上各点的切线和割线斜率基本上相同,这时切线有效压力近似等于割线有效压力.图 4中的等值线都是直线,但它们相互不平行,αs的变化范围在0.487~0.887之间.αs的变化范围宽,出现这种等值线特征的有效压力仍是非线性有效压力.图 5中的等值线基本上是相互平行的直线,这时每个测点的αt和αs相等.图 5中Barre花岗岩αs变化范围在0.795~0.824之间,变化范围很小,可以近似看成是一常数,计算得到的有效压力可以认为是线性的.当出现图 4和图 5这种曲线特征时,由于αs和αt的大小基本相等,切线有效压力、割线有效压力与渗透率的关系点基本上会重合在一起,难以比较它们之间的差别,图 8和图 9就是这种情况.
图 4和图 5这两种等值线形态,都是Bernabé[11]推测的渗透率等值线形态的特殊情况.在Bernabé的示意图中(图 1)等值线有直线和曲线,如果曲线都变成直线,就是图 4中表示的等值线形态,这时有效压力仍是非线性有效压力;如果这些直线相互平行,则变成了图 5形态,这时的有效压力就是人们熟悉的线性有效压力.从12块岩样的等值线形态特征看,Bernabé推测的岩石渗透率在围压和孔隙压图中的等值线形态和这里选取的岩芯的等值线形态是一致的.
图 7-图 10给出的测试点有效压力与渗透率的关系点分析可以看出,Terzaghi有效压力与渗透率测试点十分分散,说明用Terzaghi有效压力方程计算得到的相同有效压力下渗透率值不一样,这不符合有效压力的定义,计算得到的有效压力无实际的应用意义.12块岩芯测试点有效压力与渗透率关系图的结果看,除Barre花岗岩外,所有岩芯渗透率都不能用Terzaghi有效压力方程来计算.
Barre600花岗岩(图 7)和S4(图 10)的切线有效压力与渗透率关系点十分分散,响应面切线有效压力系数法计算得到的有效压力也就没有实际意义.除Chelmsford H、Barre、Chemlford G和Chelmsford R花岗岩外,所有岩芯的切线有效压力与渗透率关系点也都十分分散,说明大多数低渗岩石都不能用响应面切线有效压力系数法计算有效压力.Chelmsford H、Barre、Chelmsford G和Chelmsford R花岗岩渗透率等值线基本上是直线,计算得到的这4块岩芯的两种有效压力系数的差别在5%以内,这是计算得到的切线有效压力和割线有效压力基本上相等原因.而所有岩芯(如图 10)的割线有效压力和渗透率关系点基本上都落在一条线上,表明割线有效压力计算得到的有效压力更有实际的应用价值,同时也说明响应面割线有效压力系数法是计算有效压力的更为有效方法.
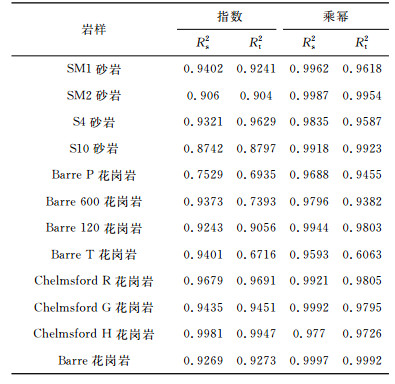
表 3中是用乘幂和指数关系拟合各种有效压力与渗透率间关系得到的结果.指数和乘幂拟合式分别是k/kref=aexp(bpeff/pref)和k/kref=c(peff/pref)d,式中kref表示参考有效压力pref下的渗透率,a、b、c和d都是拟合系数.表 3给出的相关系数显示,割线相关系数R2 s>切线相关系数R2 t,表明割线有效压力与渗透率的拟合效果好于切线有效压力与渗透率的拟合效果,进一步说明可以用割线有效压力更好地描述有效压力和渗透率间的一一对应关系.从拟合描述裂缝岩芯有效压力和渗透率关系的乘幂式子好于描述孔隙介质的有效压力和渗透率的指数关系式[8],表明裂缝的变形是造成岩芯渗透率变化的主要原因.
|
|
表 3 渗透率与有效压力之间关系的指数和乘幂拟合相关系数R2 Table 3 The coefficients of correlation R2 obtained by fitting the relationship between permeability and effective pressure with the exponential function and the power function |
(1)通过用响应面方法绘制本次实验和以往共计12块岩芯的渗透率等值图,证明Bernabé推测的渗透率等值线在围压pc和孔隙压pp图中形态是正确的.
(2)响应面割线有效压力系数法可以计算随压力连续变化的线性和非线性有效压力.无论有效压力是线性还是非线性的,计算得到的有效压力均满足有效压力的定义.
(3)割线有效压力系数法计算非线性有效压力,可以改善有效压力计算得到的渗透率的准确性.
| [1] | Fjar E, Holt R M, Raaen A M, et al. Petroleum related rock mechanics.//Developments in Petroleum Science 53. New York: Elsevier Science, 2008. |
| [2] | Robin P Y F. Note on effective pressure. J. Geophys. Res. , 1973, 78(14): 2434-2437. DOI:10.1029/JB078i014p02434 |
| [3] | Berryman J G. Effective stress for transport properties of inhomogeneous porous rock. J. Geophys. Res. , 1992, 97(B12): 17409-17424. DOI:10.1029/92JB01593 |
| [4] | Al-Wardy W, Zimmerman R W. Effective stress law for the permeability of clay-rich sandstones. J. Geophys. Res. , 2004, 109(B4): B04203. |
| [5] | Terzaghi K. Principles of soil mechanics. Eng. News Rec. , 1925, 95: 987-996. |
| [6] | Vairogs J, Hearn C L, Dareing D W, et al. Effect of rock stress on gas production from low-permeability reservoirs. Journal of Petroleum Technology , 1971, 23(9): 1161-1167. DOI:10.2118/3001-PA |
| [7] | Jones F O, Owens W W. A laboratory study of low-permeability gas sands. Journal of Petroleum Technology , 1980, 32(9): 1631-1640. DOI:10.2118/7551-PA |
| [8] | 尹尚先, 王尚旭. 不同尺度下岩层渗透性与地应力的关系及机理. 中国科学D辑:地球科学 , 2006, 49(7): 714–723. Yin S X, Wang S X. Effect and mechanism of stresses on rock permeability at different scales. Science in China Series D: Earth Sciences (in Chinese) , 2006, 49(7): 714-723. DOI:10.1007/s11430-006-0714-9 |
| [9] | Todd T, Simmons G. Effect of pore pressure on the velocity of compressional waves in low-porosity rocks. J. Geophys. Res. , 1972, 77(20): 3731-3743. DOI:10.1029/JB077i020p03731 |
| [10] | Bernabé Y. The effective pressure law for permeability in Chelmsford granite and Barre granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. , 1986, 23(3): 267-275. DOI:10.1016/0148-9062(86)90972-1 |
| [11] | Bernabé Y. The effective pressure law for permeability during pore pressure and confining pressure cycling of several crystalline rocks. J. Geophys. Res. , 1987, 92(B1): 649-657. DOI:10.1029/JB092iB01p00649 |
| [12] | Warpinski N R, Teufel L W. Determination of the effective-stress law for permeability and deformation in low-permeability rocks. SPE Form. Eval. , 1992, 7(2): 123-131. DOI:10.2118/20572-PA |
| [13] | Li M, Bernabé Y, Xiao W L, et al. Effective pressure law for permeability of E-bei sandstones. J. Geophys. Res. , 2009, 114: B07205. DOI:10.1029/2009JB006373 |
| [14] | Kranz R L, Frankel A D, Engelder T, et al. The permeability of whole and jointed Barre granite. Int. J. Rock. Min. Sci. Geomech. Abstr. , 1979, 16(4): 225-334. DOI:10.1016/0148-9062(79)91197-5 |
| [15] | Walsh J B. Effect of pore pressure and confining pressure on fracture permeability. Int. J. Rock. Min. Sci. Geomech. Abstr. , 1981, 18(5): 429-435. DOI:10.1016/0148-9062(81)90006-1 |
| [16] | Brace W F, Walsh J B, Frangos W T. Permeability of granite under high pressure. J. Geophys. Res. , 1968, 73(6): 2225-2236. DOI:10.1029/JB073i006p02225 |
| [17] | 汪荣鑫. 数理统计. 西安: 西安交通大学出版社, 2004 . Wang R X. Mathematical Statistics (in Chinese). Xi'an: Xi'an Jiaotong University Press, 2004 . |
| [18] | Box G P, Draper N R. Empirical Model-Building and Response Surfaces. New York: John Wiley & Sons Inc., 1987 . |
| [19] | 郑玲丽, 李闽, 肖文联, 等. 最大似然函数法确定渗透率有效应力系数. 新疆石油地质 , 2008, 29(6): 747–749. Zheng L L, Li M, Xiao WL, et al. Determination of effective stress coefficient of permeability using maximum-likelihood function approach. Xinjiang Petroleum Geology (in Chinese) , 2008, 29(6): 747-749. |
| [20] | 李闽, 肖文联, 郭肖, 等. 塔巴庙低渗致密砂岩渗透率有效应力定律实验研究. 地球物理学报 , 2009, 52(12): 3166–3174. Li M, Xiao W L, Guo X, et al. Laboratory study of the effective pressure law for permeability in Ta-Ba-Miao low-permeability sandstones. Chinese Journal of Geophysics (in Chinese) , 2009, 52(12): 3166-3174. |
| [21] | 李闽, 肖文联. 低渗砂岩储层渗透率有效应力定律试验研究. 岩土力学与工程学报 , 2008, 27(S2): 3535–3540. Li M, Xiao W L. Experimental study on permeability-effective-stress law in low-permeability sandstone reservoir. Chinese Journal of Rock Mechanics and Engineering (in Chinese) , 2008, 27(S2): 3535-3540. |
| [22] | 郑玲丽, 李闽, 钟水清, 等. 变围压循环下低渗透致密砂岩有效应力方程研究. 石油学报 , 2009, 30(4): 588–592. Zheng L L, Li M, Zhong S Q, et al. Research on calculation of effective stress in low-permeability sandstone rock under cyclic loading and unloading. Acta Petrolei Sinica (in Chinese) , 2009, 30(4): 588-592. |
| [23] | A PI. Recommended Practice for Determining Permeability of Porous Media. (Vol. 27). Dallas: API, 1956 . |
| [24] | 何更生, 唐海. 油层物理(第二版). 北京: 石油工业出版社, 2011 . He G S, Tang H. Petrophysics, 2nd ed (in Chinese). Beijing: Petroleum Industry Press, 2011 . |
| [25] | The Japan Society of Mechanical Engineers. JSME Data Book: Thermophysical Properties of Fluids. The Japan Society of Mechanical Engineers, 1983. |
| [26] | 吴曼, 杨晓松, 陈建业. 超低渗透率测量仪的测试标定及初步测量结果. 地震地质 , 2011, 33(3): 719–735. Wu M, Yang X S, Chen J Y. The calibration of ultralow permeability measurement apparatus and preliminary experimental results. Seismology and Geology (in Chinese) , 2011, 33(3): 719-735. |
 2013, Vol. 56
2013, Vol. 56