2. 中海油研究总院, 北京 100027;
3. 中石化勘探开发研究院油气地球物理研究中心, 北京 100083
2. Science and Technology Development Department of China National Offshore Oil Corp, Beijing 100027, China;
3. Geophysical Research Center, SINOPEC Exploration & Production Research Institute, Beijing 100083, China
偏移是地震成像技术中最重要的环节之一,Kirchhoff叠前时间偏移对观测系统适应性强、计算成本低,在生产中应用广泛.Kirchhoff叠前时间偏移的关键技术之一是计算地震波走时,为了使其获得较高的精度,前人做过很多工作.目前叠前时间偏移走时方程中常见的有:二阶双曲NMO方程、时移双曲NMO方程[1]、六阶近似NMO方程[2]、Alkhalifah连分式逼近NMO方程[3-4]、射线追踪时差方程[5]、分式展开二次方程[6]以及基于李群算法和拟微分算子象征理论的非对称走时[7]方程等.切比雪夫多项式在逼近理论中有重要的应用[8-10],本文提出基于第一类切比雪夫多项式的非对称走时方程,该方程能在对称弯曲射线走时方程的基础上添加切比雪夫非对称项,达到计算量少,计算精度高的效果.
在油气勘探开发的地震方法中,角度域共成像道集(ADCIG)是连接地震数据处理与储层反演的重要纽带.为抽取更准确的时间域ADCIG,对走时计算加以改进一直是研究的热点.自1990年de Bruin提出计算地震数据反射系数随角度变化开始[11],国内外很多学者对ADCIG开展了一系列的研究工作,成为近年来的研究热点之一.角道集主要有以下几点应用:其一,基于共成像道集的偏移速度分析[12-13],在ADCIG上,当偏移速度与实际速度一致时,道集的同相轴曲线不随入射角的变化而变化,是拉平的,当偏移速度与实际速度不一致时,道集的同相轴曲线就随入射角增大上翘或者下弯;其二,在ADCIG上可以进行AVA分析[14];其三,可对角道集进行适当的去噪、剩余曲率校正等处理,由于角度域共成像点道集能够提供其它类型道集上不易表示的地震波信息,因此实施有针对性的数据处理后再叠加成像,可提高成像的质量[15].角道集研究用于叠前深度偏移(PSDM)的较多[16-17],但PSDM速度建模困难,计算效率低,而叠前时间偏移(PSTM)角道集的获取效率较高[18],因此基于PSTM方法的角道集研究得以展开.近年来,针对PSTM的ADCIG研究方法有,基于直射线近似的Kirchhoff积分角度域成像方法[19],基于射线追踪的表驱Kirchhoff叠前时间偏移角度域算法以及非双曲时差方位/角度域叠前时间偏移方法[5],基于平面波分解的射线参数域成像道集方法[20],基于李代数的非对称走时角道集获取方法[21]等.本文角道集的获得采用基于切比雪夫多项式的非对称弯曲射线走时.
2 方法原理 2.1 切比雪夫多项式非对称走时计算方法 2.1.1 第一类切比雪夫多项式基本概念切比雪夫多项式与棣美弗定理有关,是以递归方式定义的一系列正交多项式序列.第n阶第一类切比雪夫多项式以符号Tn表示.第一类切比雪夫多项式有自变量w介于-1和1之间的均匀分布的n个零点和n+1个极值点,其最大误差在各种级数中是最小的,它的根可以用于多项式插值,相应的插值多项式能最大限度地降低龙格现象[8-10],并且提供多项式连续函数的最佳一致逼近.其递推公式为
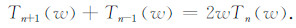
|
(1) |
文中用到的第一类切比雪夫多项式的前几项可以写为
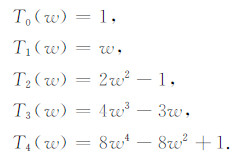
|
(2) |
相对应的,
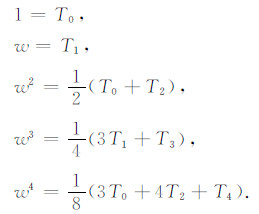
|
(3) |
Slotnick于1959年[22]根据Snell定律,给出了射线参数表征的地震反射波时距曲线方程(4)和(5):
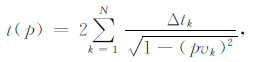
|
(4) |
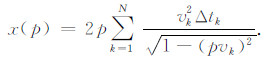
|
(5) |
t(p)为射线走时,x(p)为偏移距,p为射线参数,vk为第k层地震波波速,Δtk为第k层垂直射线走时.
求解此方程的方法以对称走时理论方法居多. Taner和Koehler于1969年将方程(4)、(5)进行Taylor展开[23],得到了对称弯曲射线走时方程(6).通常情况下,为求得高精度的走时计算式,有两类方法:一种是对泰勒展开项的系数进行优化,一种是采用高阶走时计算式[4].具体而言,优化六阶的走时精度是目前精度比较高的.不过,两种方法各有不足:采用高阶走时计算式会增加计算量,尤其在计算大规模地震数据时所需计算时间较长;而采用优化泰勒系数的方法时,需要先对走时计算式进行优化,目前优化方法主要是六阶优化方程方法[2]和四、六阶调节系数走时方程方法[4],因为两者的阶数比较高,所以并没有减少计算量.以上情况限制了高精度计算走时在实际生产中的应用.而本文提出切比雪夫三阶优化走时,既能节省计算量,又能保证较高的精度.
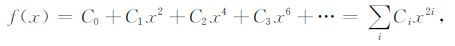
|
(6) |
其中各个系数为
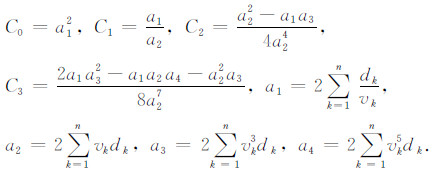
|
dk为第k层厚度.
2.1.3 切比雪夫多项式非对称走时方程在泰勒展开式中,偏移距x属于(k1,k2)区间,设w=(x-q)/p,q=(k1+k2)/2,p=(k2-k1)/2,即可将f(x)等价变化到f(w),w属于(-1,1),于是,C'i=f(ai,p,q),将四阶泰勒展开走时方程等价变化为
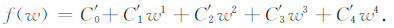
|
(7) |
这时,用第一类切比雪夫多项式对f(w)进行转化,得到:
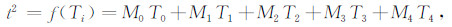
|
(8) |
式中Mi=f(Cj),截去高阶项T4,再反变换回f(x),最终得到:
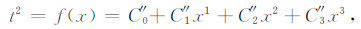
|
(9) |
x1对公式的误差影响较大,且有碍于优化,去掉此项,并赋予x3一调节系数m,用于调节截取的误差,赋予其初始值m=1,得到:
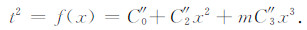
|
(10) |
本文以模拟退火法对m进行优化,用此式逼近弯曲射线优化六阶泰勒走时的精度,即可将m优化得到值m',最终的切比雪夫多项式非对称走时方程如下:
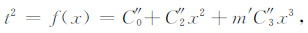
|
(11) |
需要注意的是,在优化m的时候,会增加一定的复杂性:一般在偏移孔径内,优化一个m'即可,但如果数据要求进行长偏移距的走时计算,则需要进行分段优化[10],使得不同偏移距范围具有不同的m'值;另一方面,与泰勒展开走时计算等常规方法相比,优化m本身虽然多了一步工作量,不过优化步骤并不会消耗大量的计算时间.
设计一个三层水平层状模型进行走时分析与验证,如图 1所示,网格大小为400×800,网格间距比例为10m,即模型X方向8000m,Z方向4000m.在对模型正演时,采样间隔4 ms,采样时长6s,观测系统采用全局接收,道间距20 m,炮点位置选择在模型网格点坐标(1,1)处.用单炮数据对m进行优化.

|
图 1 水平三层速度模型 Fig. 1 3 layers velocity model |
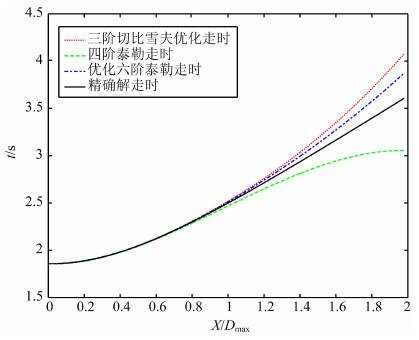
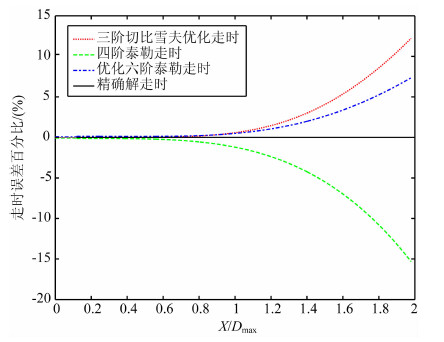
在图 2的走时精度分析与图 3走时误差对比中,横坐标X/Dmax为偏移距X与最大深度Dmax的比值.在走时计算式中,四阶泰勒走时具有计算量低的优点,六阶优化泰勒走时具有精度高的优点,本文将优化三阶切比雪夫走时与上述两者进行比较,如图 2和图 3,证明优化后的三阶切比雪夫走时比高阶的四阶泰勒走时精度高,接近更高精度的优化六阶泰勒走时.并且由走时计算公式可以很明显的发现,优化三阶切比雪夫走时的计算量在三者中是最小的.
|
图 2 走时精度分析 Fig. 2 Analysis of travel time |
|
图 3 走时误差对比 Fig. 3 Analysis of travel time errors |
可以输入任一未经偏移的地震道集,见图 4.对于输入的每一道地震数据,扫描地下成像点,入射线走时为ts,反射线走时为tr.角度计算采用公式(12)、(13),此种计算方法考虑射线弯曲效应,计算地下散射点处真实的地震射线角度[21].
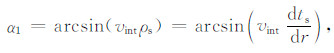
|
(12) |
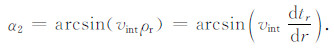
|
(13) |
如图 4,当满足ts+tr=ti时,将地震道上对应的ti时刻的能量e加权归位到成像点对应的iz时刻上,加权采用保幅权因子[24]公式(14):
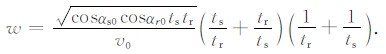
|
(14) |
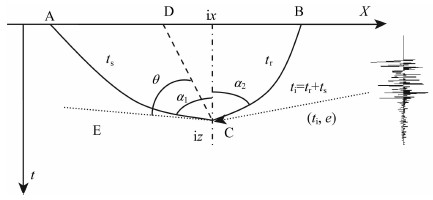
把所有地震道依次这样处理后将同一成像点相同角度能量叠加,不同角度横向排列,便可得到ix成像点的角度域共成像点道集.依次类推,便可以求得各个成像点的角道集.这样求取角道集的方法能克服水平层状介质限制,考虑地层倾斜影响,可以求得真实入射角度,使能量正确归位,并且可以由原始的地震数据中直接求得角道集.
|
图 4 地震道ti时刻有能量e,C为地下iz时间点处一成像点,ACB为地震弯曲射线路径,EC为弯曲射线在C处的切线,α1为AC与铅垂线的夹角,α2为BC与铅垂线的夹角.θ=(α1+α2)/2为射线在C点的真实入射角度 Fig. 4 ti point on a seismic trace is corresponding to the energy e.C is a time image point at iz.ACB is a bend-ray where EC is the tangent at C.α1、α2 are the angles the bend-ray corresponding to the plumb line.And θ is the angle of incidence we need |
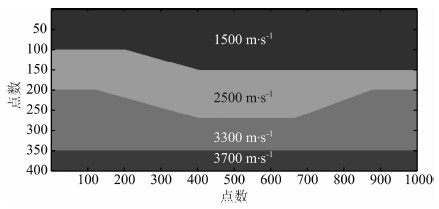
采用数据模型,见图 5,横向1000点纵向400点,样点间隔均为10 m,采样间隔4 ms,采样时长6s,观测系统采用全局接收,炮间距40 m,道间距20m,共250炮.角度分辨率为1°.我们计算如图水平方向280号CMP坡度点处的ADCIG.
|
图 5 四层速度模型 Fig. 5 4 layers model |
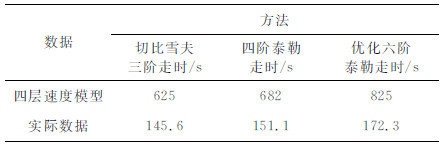
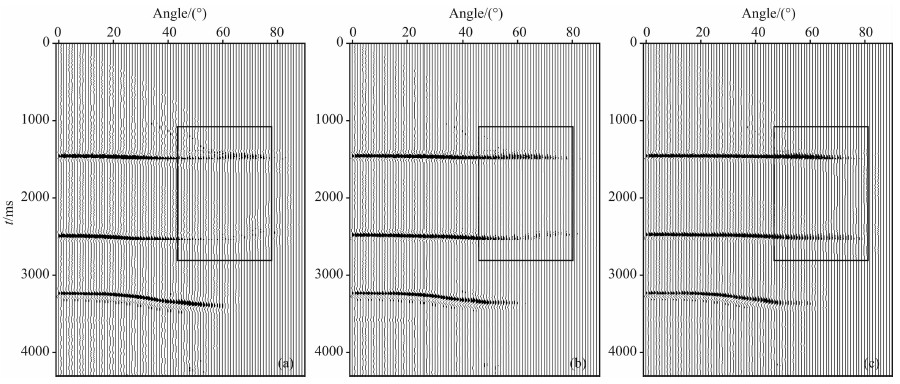
由图 6所示可以发现,经切比雪夫改进的三阶非对称走时计算方法计算出的角道集,其精度与图 6c优化六阶泰勒走时展开的精度十分接近;与图 6a四阶泰勒走时计算方法相比,其第二层大角度处的同相轴有所延长,且更加连续、平整,能量也得以较为准确的归位.在表 1中列出了只改变走时计算方法的情况下三种计算方法所需时间.表 1给出的数据说明,三阶切比雪夫非对称走时方法在时间上比泰勒四阶走时快8.4%,比优化六阶泰勒走时快24.2%.即证明,经切比雪夫多项式改进求得的非对称走时同时具备计算量较少和精度较高的优势.
|
图 6 四阶泰勒展开走时ADCIG(a);改进的切比雪夫三阶非对称走时ADCIG(b);优化六阶泰勒展开走时的ADCIG(c) Fig. 6 Shows the 4-order taylor method result (a); Shows the optimized 3-order asymmetric Chebyshev method result (b); Shows the optimized 6-order taylor method result (c) |
|
|
表 1 走时计算量统计与对比 Table 1 Contrast of the 3 travel-time calculation methods |
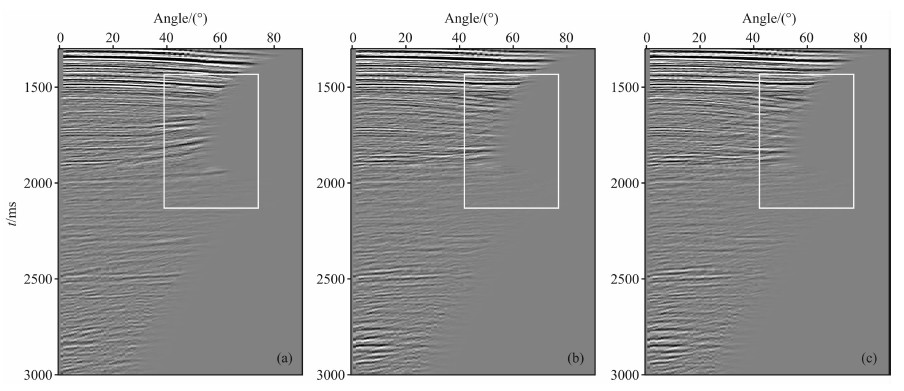
取某一实际数据为例,offset范围(100m,4875m),道间隔25m,角度分辨率为1°,见图 7,文中显示了从1300ms到3000ms的三种不同计算走时得出的同一成像点的角道集.
|
图 7 四阶泰勒展开走时的ADCIG(a);改进的切比雪夫三阶非对称走时ADCIG(b);优化六阶泰勒展开走时的ADCIG(c) Fig. 7 Shows the 4-order taylor method result (a), Shows the optimized 3-order asymmetric Chebyshev method result (b), Shows the optimized 6-order taylor method result (c) |
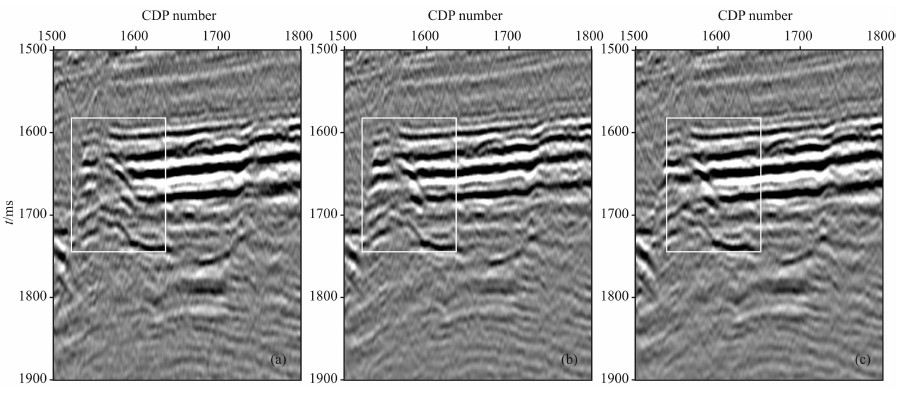
如图 7b中三阶切比雪夫非对称走时的计算方法精度较高,其ADCIG同相轴与图 7c优化六阶泰勒对称走时展开的结果精度几乎一样,比图 7a四阶泰勒走时的结果同相轴更加平整.在表 1中列出了在计算该成像点时,三种计算方法计算时间的对比.表 1给出的数据说明,求取此成像点的ADCIG采用经切比雪夫改进的三阶非对称走时方法比四阶泰勒走时的计算结果相对缩短了约3.6%.图 8列举了三种走时方法计算出的角道集经过叠加后的最终剖面的一部分,可以看出,圈出部分的同相轴的连续性和清晰度由不好到较好到很好的变化.由此得到与模型数据相同的结果,即,经切比雪夫多项式改进求得的非对称走时同时具备计算量较少和精度较高的优势.
|
图 8 四阶泰勒展开走时的剖面(a);改进的切比雪夫三阶非对称走时的剖面(b);优化六阶泰勒展开走时的剖面(c) Fig. 8 Shows the 4-order taylor method profile result (a), Shows the optimized 3-order asymmetric Chebyshev method profile result (b); shows the optimized 6-order taylor profile result (c) |
本文引进第一类切比雪夫多项式,对泰勒展开对称走时进行改进,推导出非对称走时奇数项,得到低阶切比雪夫非对称走时计算公式,通过在数值模型和实际数据中抽取角道集的实验,取得了较好的结果,验证了该方法具有高阶走时的精度,同时比实际生产中较为广泛应用的低阶高精度走时消耗更少的计算量,而且应用这种走时直接求得的角道集,能较真实的反映地震射线在地下层位的入射角度.
切比雪夫非对称走时与基于李代数理论的非对称走时[7, 25]具有不同的理论计算公式,切比雪夫非对称走时的计算量较小,在实际应用中有一定的优势.
在切比雪夫非对称走时计算中,优化算子m'的取值较为关键.针对不同的地震数据,k1、k2值各有不同,优化方法也可以根据情况择优选取,因此优化得到的m'值也不尽一致,但一般情况下都可以达到计算量较小和精度较高的计算效果.
| [1] | Castle R J. A theory of normal moveout. Geophysics , 1994, 59(6): 983-999. DOI:10.1190/1.1443658 |
| [2] | Sun C W, Wang H W, Nartinez R D. Optimized 6th order NMO correction for long-offset seismic data. 72nd Annual International Meeting, SEG, Expanded Abstracts, 2002. |
| [3] | Alkhalifah T, Tsvankin I. Velocity analysis for transversely isotropic media. Geophysics , 1995, 60(5): 1550-1566. DOI:10.1190/1.1443888 |
| [4] | 尤建军, 常旭, 刘伊克. VTI介质长偏移距非双曲动校正公式优化. 地球物理学报 , 2006, 49(6): 1770–1778. You J J, Chang X, Liu Y K. Optimization of nonhyperbolic moveout correction equation of long-offset seismic data in VTI media. Chinese J. Geophys.(in Chinese) (in Chinese) , 2006, 49(6): 1770-1778. |
| [5] | 程玖兵, 王楠, 马在田. 表驱三维角度域Kirchhoff叠前时间偏移成像方法. 地球物理学报 , 2009, 52(3): 792–800. Cheng J B, Wang N, Ma Z T. Table-driven 3-D angle-domain imaging approach for Kirchhoff prestack time migration. Chinese J. Geophys.(in Chinese) (in Chinese) , 2009, 52(3): 792-800. |
| [6] | 刘洋. 反射波分式展开时距方程及其精度分析. 石油物探 , 2003, 42(4): 441–447. Liu Y. Fraction expansion time-distance equation of reflection wave and its accuracy analysis. Geophysical Progress for Petroleum (in Chinese) (in Chinese) , 2003, 42(4): 441-447. |
| [7] | 刘洪, 刘国锋, 李博, 等. 基于横向导数的走时计算方法及其在叠前时间偏移中的应用. 石油物探 , 2009, 48(1): 3–10. Liu H, Liu G F, Li B, et al. The travel time calculation method via lateral derivative of velocity and its application in pre-stack time migration. Geophysical Progress for Petroleum (in Chinese) (in Chinese) , 2009, 48(1): 3-10. |
| [8] | Zhang J H, Wang W M, Wang S Q. Optimized Chebyshev Fourier migration: A wide-angle dual-domain method for media with strong velocity contrasts. Geophysics , 2010, 75(2): S23-S24. DOI:10.1190/1.3350861 |
| [9] | 丁帆, 张金海, 姚振兴. 长偏移距地震资料的优化契比雪夫动校正方法. 地球物理学进展 , 2011, 26(3): 836–842. Ding F, Zhang J H, Yao Z X. Optimized Chebyshev method for normal moveout of long-offset seismic data. Progress in Geophysics (in Chinese) (in Chinese) , 2011, 26(3): 836-842. |
| [10] | 刘璐, 梁光河, 符超, 等. 基于Chebyshev多项式的弯曲射线Kirchhoff叠前时间偏移. 地球物理学报 , 2011, 54(10): 2665–2672. Liu L, Liang G H, Fu C, et al. Bend-ray Kirchhoff pre-stack time migration based on Chebyshev polynomial. Chinese J. Geophys.(in Chinese) (in Chinese) , 2011, 54(10): 2665-2672. |
| [11] | de Bruin, C G M, Wapenaar C P A, Berkhout A J. Angle-dependent reflectivity by means of prestack migration. Geophysics , 1990, 55(9): 1223-1234. DOI:10.1190/1.1442938 |
| [12] | Biondo B, William W S. Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging. Geophysics , 2004, 69(5): 1283-1298. DOI:10.1190/1.1801945 |
| [13] | 刘奇琳, 刘伊克, 常旭. 双平方根波动方程偏移速度分析. 地球物理学报 , 2009, 52(7): 1891–1898. Liu Q L, Liu Y K, Chang X. Wave-equation migration velocity analysis by double square root method. Chinese J. Geophys.(in Chinese) (in Chinese) , 2009, 52(7): 1891-1898. |
| [14] | Brandsberg-Dahl S, de Hoop M V, Ursin B. Focusing in dip and AVA compensation on scattering-angle/azimuth common image gathers. Geophysics , 2003, 68(1): 232-254. DOI:10.1190/1.1543210 |
| [15] | Lee S, King D, Lin S. Efficient true-amplitude weights in Kirchhoff time migration. 74th Annual International Meeting, SEG, Expanded Abstracts, 2004: 1089-1092. |
| [16] | Rickett J, Sava P. Offset and angle-domain common image-point gathers for shot-profile migration. Geophysics , 2002, 67(3): 883-889. DOI:10.1190/1.1484531 |
| [17] | 陈凌, 吴如山, 王伟君. 基于Gabor-Daubechies小波束叠前深度偏移的角度域共成像道集. 地球物理学报 , 2004, 47(5): 876–885. Chen L, Wu R S, Wang W J. Common angle image gathers obtained from Gabor-daubechies beamlet prestack depth migration. Chinese J. Geophys.(in Chinese) (in Chinese) , 2004, 47(5): 876-885. |
| [18] | Sava P, Fomel S. Angle-domain common-image gathers by wavefield continuation methods. Geophysics , 2003, 68(3): 1065-1074. DOI:10.1190/1.1581078 |
| [19] | Perez G, Marfurt K J. Improving lateral and vertical resolution of seismic images by correcting for wavelet stretch in common-angle migration. Geophysics , 2007, 72(6): 94-104. |
| [20] | 王棣, 王华忠, 马在田, 等. 叠前时间偏移方法综述. 勘探地球物理进展 , 2004, 27(5): 313–316. Wang D, Wang H Z, Ma Z T, et al. Review of prestack time migration methods. Progress in Exploration Geophysics (in Chinese) (in Chinese) , 2004, 27(5): 313-316. |
| [21] | 邹振, 刘洪, 刘红伟. Kirchhoff叠前时间偏移角度道集. 地球物理学报 , 2010, 53(5): 1207–1214. Zou Z, Liu H, Liu H W. Common-angle gathers based on Kirchhoff pre-stack time migration. Chinese J. Geophys.(in Chinese). (in Chinese) , 2010, 53(5): 1207-1214. |
| [22] | Slotnick M. Lessons in Seismic Computing: A Memorial to the Author. Lawrence: Society of Exploration Geophysicists, 1959. |
| [23] | Taner M T, Koehler F. Velocity spectra-digital computer derivation applications of velocity functions. Geophysics , 1969, 34(6): 859-881. DOI:10.1190/1.1440058 |
| [24] | Dellinger J A, Gray S H, Murphy G E, et al. Efficient 2. 5-Dtrue-amplitude migration. Geophysics , 2000, 65(3): 943-950. |
| [25] | 张廉萍, 刘洪. 适于Kirchhoff叠前深度偏移的地震走时李代数积分算法. 地球物理学报 , 2010, 53(8): 1893–1901. Zhang L P, Liu H. Lie algebra integral algorithm of travel-time calculation for pre-stack Kirchhoff depth migration. Chinese J. Geophys.(in Chinese) (in Chinese) , 2010, 53(8): 1893-1901. |
 2013, Vol. 56
2013, Vol. 56