2. 中国科学技术大学地球和空间科学学院, 合肥 230026
2. School of Earth and Space Science, University of Science and Technology of China, Hefei 230026, China
大量野外观测研究表明,许多地震过程中伴随发生不同程度的电磁辐射异常现象,例如,Matsushim等[1]记录了1999年İzmit7.4级地震及其余震过程中的电场和磁场,Karakelian等[2]记录到了1999年Hector Mine7.1级地震过程中的电磁场,汤吉等[3-4]在武都汉王地震台附近监测到了汶川地震余震事件的同震电磁信号,并指出电磁场和地震波在波形和频率上都具有良好的一致性.事实上早在1939年Ivanov[5]就发现了流动电势效应---E效应,即在不施加外加电场的情况下,记录到了地震波产生的电场.为解释这一现象,Frenkel[6]建立了一套震电方程组,该方程组描述了孔隙介质中固-液相对运动而产生的流动电流,但是并未考虑辐射电磁波的问题.在此基础上,Pride[7]通过体积平均方法推导出了一套更为完整的流体饱和孔隙介质中的震电波场控制方程组,为之后的震电效应研究提供了基础.
在震电问题的数值模拟方面,Haartsen & Pride[8]利用全局矩阵方法对层状介质中点源激发的震电波场进行了研究,结果表明存在两种类型的电磁波:一种是地震波在其经过的地方激发的伴随电磁波,其存在依赖于地震波的传播;另一种是当地震波经过介质分界面时,会产生独立于地震波传播的辐射电磁场,以电磁波速度传播.Garambois & Dietrich[9]进一步对水平层状介质中点震源激发的震电波场进行了系统的研究,并探讨了电磁信号对介质参数变化的响应.但整体而言,针对孔隙介质震电波场的数值模拟研究并不太多.最近,随着合成地震图的数值算法的发展(例如,Chen[10]和Ge & Chen[11]发展的广义反透射系数方法已在合成地震图的数值模拟研究中被证实具有稳定、高效和适用范围较广等特点),Ren等[12-13]将广义反透射系数方法拓展到了孔隙介质中震电波场的数值模拟研究中,得到了一套计算点源激发的震电波场的数值模拟方法.
在震电的野外试验和室内实验方面,Martner & Sparks[14],Thompson & Gist[15-16]和Zhu等[17-19]等工作均表明含流体孔隙介质中的地震波可以激发电磁信号,利用震电转换可以探测一定深度的油气储层分界面.由于震电效应能同时反映介质弹性参数和电性参数的变化,基于震电效应的震电勘探作为一种潜在的油气勘探方法受到了地球物理学界的重视.
上述学者的研究大多侧重勘探领域(例如,数值模拟局限于爆炸点源或单力点源),虽然震电效应在天然地震监测和预警研究方面也具有潜在的应用价值,但是与之相关的报道和研究甚少[20].目前,Gao等[21]模拟了双力偶点源激发的地震电磁波场,Hu等[22]研究分析了有限断层在地表附近激发的地震电磁波场,Ren等[23]将爆炸源和单力点源逐步拓展到双力偶点源和有限断层面源的模型,实现了相应模型的震电波场数值模拟算法,Gao等[24-25]模拟了地震发生时刻产生的电磁信号,并研究了该信号随介质参数的变化响应.但以上工作尚未深入研究震源类型等参数对结果的影响.对孔隙介质中震电波场认识比较有限的现状直接制约了地震电磁机理研究的进一步开展.有鉴于此,本文利用Ren等[23]的方法对双力偶点源以及有限断层面源在不同模型下产生的电磁信号进行了数值模拟,考察了地震波和电磁信号的相关性,并讨论了不同的震源时间函数类型和不同的Ricker子波峰值频率对地震和电磁信号的影响.
2 方法Pride[7]用体积平均方法建立了一套震电波场宏观控制方程组,该方程组描述了流体饱和孔隙介质中地震波和电磁场的相互耦合以及震电波场在介质中的传播(具体公式详见附录A).应该指出,该理论假设双相介质中的孔隙是连通的并且被流体充满,而实际孔隙介质可能并非完全如此,所以Pride的震电控制方程组有其局限性.尽管如此,目前该理论依然是震电效应研究中最受关注的一种理论.
基于Pride提出的震电波场宏观控制方程组,Ren等[23]结合前人的研究成果,利用Ge & Chen[11]发展的直接计算广义反透射系数的方法,得到了一套流体饱和层状孔隙介质中点源激发震电波场的数值模拟方法,并且基于点源叠加原理发展了有限断层面源激发的震电波场的数值模拟方法.该方法首先是在柱坐标下用一套基函数分解震电控制方程中所有的矢量和标量,得到两套方程组,分别对应于SHTE模式和PSVTM模式(在SHTE模式中,SH波产生与它运动方向相同的电流,形成TE模式的电磁场;在PSVTM模式中,PSV波产生的电流位于PSV波运动面内,形成TM模式的电磁场),具体公式详见附录B,然后根据位移-电磁场-应力的连续性边界条件得到各个界面上广义反透射系数的具体表达式,进而得到震电波场在频率域的解.最后通过离散波数法[26]得到时间域的震电波场的解.
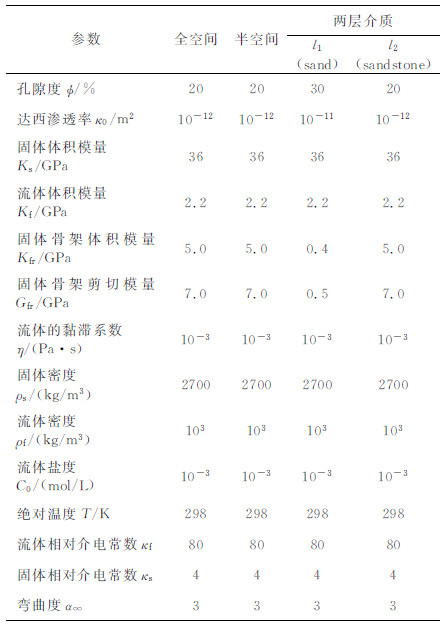
3 结果 3.1 双力偶点源激发的震电波场本节利用上述基本理论和数值模拟方法,对均匀全空间中双力偶点源激发的震电波场进行数值模拟.如图 1所示x-o-y平面位于水平位置,z轴垂直向下.图 1(a、b)为双力偶点源,其地震矩Mzx=Mxz=1.12×1014 N·m.图 1(c、d)为有限断层面源,大小为8 km×5 km,长度方向与x轴方向平行;断层倾角为60°,滑移角为0°,地震矩为M0=1.12×1017 N·m. 图 1所示模型中震源时间函数均采用峰值频率为1 Hz的Ricker子波,其时间偏移量为6 s,震源中心位置均为(0,0,10 km),接收点位于(3 km,4 km,0.05 km).图 1(a、c)为均匀半空间模型,图 1(b、d)为双层介质模型,不同模型下的介质参数选取详见表 1.
|
图 1 双力偶点源作用下的(a)半空间、(b)双层介质模型和有限断层面源作用下的(c)半空间、(d)双层介质模型 Fig. 1 (a) half space, (b) two-layer model induced by a double couple point source and (c) half space, (d) two-layer model induced by a finite fault planar source |
|
|
表 1 均匀层状介质的参数 Table 1 Properties of the layered porous media |
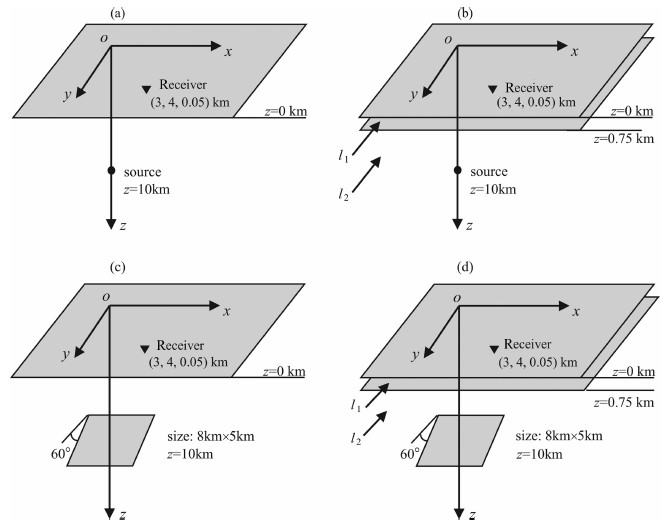
图 2是均匀全空间模型(图 1a的半空间模型去掉自由表面)在双力偶点源激发下产生的地震电磁信号,图中自上而下分别表示位移场、电场、磁场的x、y和z分量.可清晰地分辨出由Ricker子波激发产生的P波和S波扰动,到达时间大约为9.035 s和11.438 s.伴随地震波到达的电场信号在三个分量上都能清晰的看到.从图 2中可以看到S波激发同震电场信号的能力要明显弱于P波.事实上,在我们的数值模拟过程中发现,对于一些介质,S波激发的同震电场信号相较P波而言弱到几乎可以忽略.总体来说,对于大多数的孔隙介质,P波激发同震电场信号的能力要明显强于S波[8-9, 13, 20, 23],但是Gao & Hu[20]指出对于某些实际的沉积岩,S波激发同震电场信号的振幅有可能超过P波激发的同震电场信号.由于P波不产生同震磁场信号,故仅在S波到达的时间处有磁场信号.
|
图 2 均匀全空间双力偶点源激发的(a)地震波、(b)电场和(c)磁场信号示意图 Fig. 2 (a) Seismic waves, (b) electric field, and (c) magnetic field generated by a double couple point source in a homogenous full space |
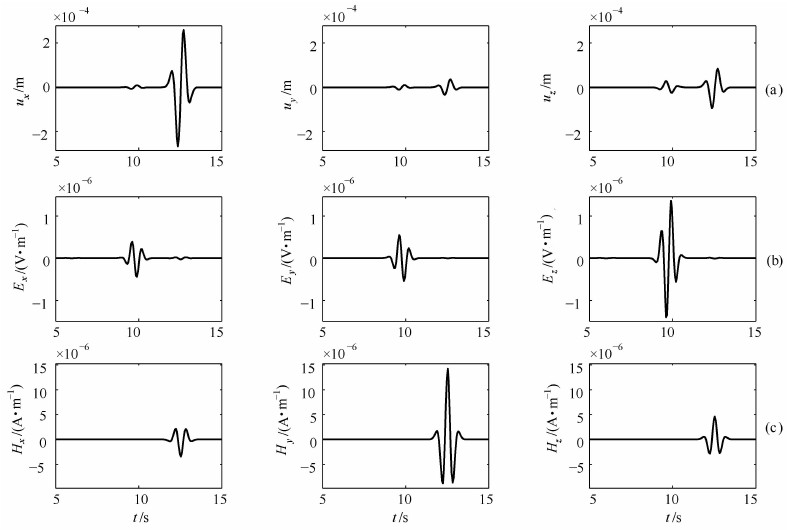
为了进一步考察均匀全空间中双力偶点源激发的地震电磁信号的特征,我们计算了图 2对应波场的频率域响应(图 3).对于采用的峰值频率为1 Hz的Ricker子波,其频谱成分主要集中在0~3 Hz.从图中可以看出产生的地震电磁信号频谱成分与子波一致,其频率集中在0~3 Hz,并且震电波场九个分量都具有相近的优势频率.结合图 2和图 3,位移场信号和电磁信号在到达时间和频率上都有较好的一致性和相关性,其中到时一致性的特征与前人的研究结果[8-9, 21-23]相吻合;汤吉等[4]开展了汶川地震强余震的同震电磁信号的实际观测,也发现地震波和电磁场在到时方面具有较好的一致性.
|
图 3 均匀全空间双力偶点源激发的(a)地震波、(b)电场和(c)磁场信号频谱示意图 Fig. 3 Frequency spectrum of (a) seismic waves, (b) electric field, and (c) magnetic field generated by a double couple point source in a homogenous full space |
本节将对双力偶点源激发的全空间(图 1a的半空间模型去掉自由表面)、半空间(图 1a)和两层介质模型(图 1b),以及有限断层面源作用下的半空间(图 1c)和两层介质模型(图 1d)进行对比,分析模型结构对地震电磁信号的影响.
图 4展示了全空间、半空间、双层介质模型中双力偶点源和有限断层面源激发产生的震电波场的Ex分量.全空间模型中双力偶点源激发的Ex分量可清晰地分辨出在伴随P波以及S波的电场信号先后到达接收点,并且伴随P波的电场信号强于伴随S波到达的电场.半空间模型中双力偶点源激发的震电波场中,由于一般情况下P波产生同震电场信号的能力强于S波激发同震电场信号的能力,在自由界面处的Sv-P转换波加强了在大约t=11.438 s时刻到达的电场信号(图 4b).
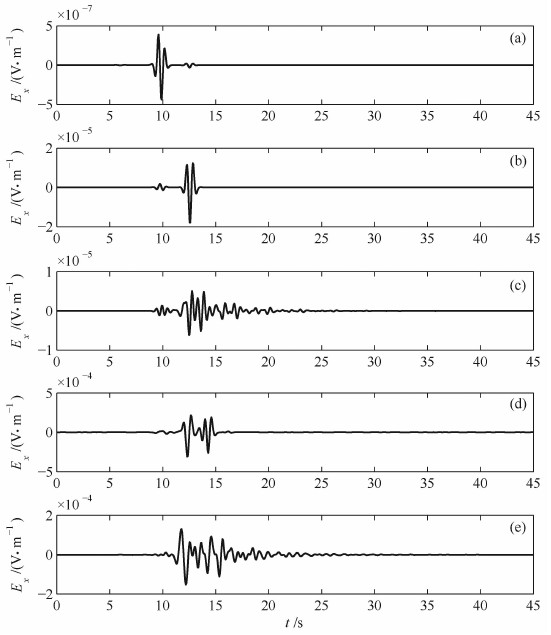
|
图 4 双力偶点源(a)全空间、(b)半空间、(c)两层介质以及有限断层面源(d)半空间、(e)两层介质模型下的电场信号Ex示意图 Fig. 4 Ex of (a) full space, (b) half space, (c) two-layer model with a double couple source, and Ex of (d) half space, (e) two-layer model with a finite fault source |
与双力偶点源相比,有限断层面源产生的地震电磁信号在波形(图 4)和频谱特征(图 5)方面均发生明显变化,并且持续时间显著增加(图 4).此外,无论是双力偶点源还是有限断层面源,两层介质模型产生的地震电磁信号的波形都比均匀半空间模型的更为复杂,持续时间也更长(图 4).
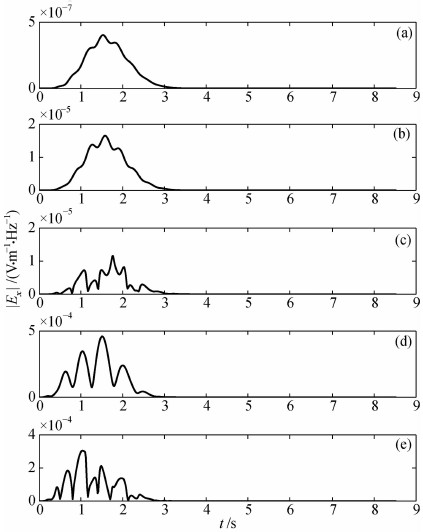
|
图 5 双力偶点源(a)全空间、(b)半空间、(c)两层介质以及有限断层面源(d)半空间、(e)两层介质模型下的电场信号Ex频谱示意图 Fig. 5 Frequencyspectrum of Ex(a) full space, (b) half space, (c) two-layer model with a double couple source, and Ex of (d) half space, (e) two-layer model with a finite fault source |
图 6表示了Ricker子波、梯形函数、指数函数、Herrmann函数对应的震源时间函数.4种子波激发类型在时间域呈现不同的模式,为了便于比较,所设计的上述4种时间函数的时间窗都为2 s,所选Ricker子波的峰值频率为1 Hz,其频谱成分主要集中在0~3 Hz,而梯形函数和指数函数采用汉宁窗滤波,滤波器的频带范围为0~3 Hz.
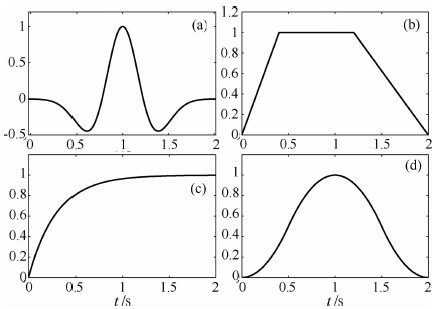
|
图 6 (a)Ricker子波、(b)梯形函数、(c)指数函数和(d)Herrmann函数对应的震源时间函数示意图 Fig. 6 Source time functions of (a) Ricker wavelet, (b) trapezoid, (c) exponential and (d) Herrmann function |
图 7表示了均匀半空间模型中双力偶点源激发下,分别采取图 6所示的Ricker子波、梯形函数、指数函数、Herrmann函数[27]4种不同震源时间函数产生的地震电磁响应,模型均采取相同的地震矩Mxz=Mzx=1.12×1014 N·m,震源位置均为(0,0,10 km),接收点均位于(3 km,4 km,0.05 km).图 7的结果显示:图 6所示的不同震源时间函数激发的地震电磁信号的波形具有比较相似的整体特征,但具体的波形细节和振幅也存在一定的差异,其中,Ricker子波产生的信号幅值最大,其对应的震电波场中可以清晰地分辨出伴随P波以及S波的电场信号,而其他函数所产生的地震电磁辐射波形幅度相对较小,并且梯形函数和Herrmann函数对应的震电波场相对较复杂.
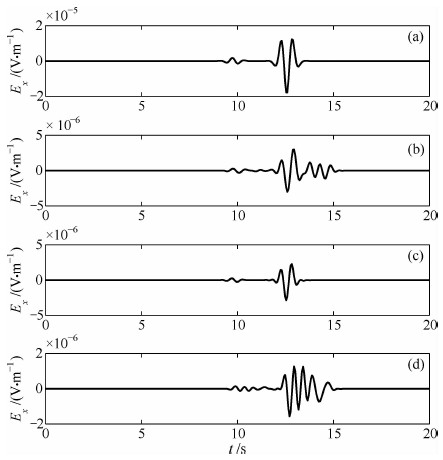
|
图 7 震源时间函数为(a)Ricker子波、(b)梯形函数、(c)指数函数和(d)Herrmann函数所产生的电场信号Ex示意图 Fig. 7 Ex of (a) Ricker wavelet, (b) trapezoid function, (c) exponent function and (d) Herrmann function as source time function |
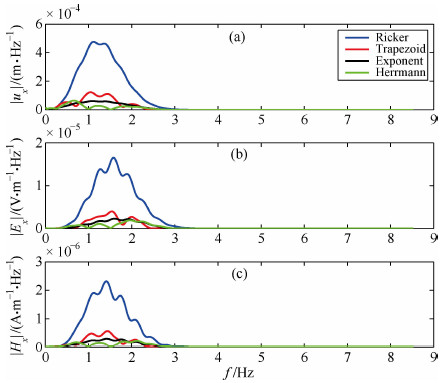
为了考察信号的频谱特征,作为一个例子,图 8给出了上述Ricker子波、梯形函数、指数函数和Herrmann函数震源时间函数所产生的地震电磁信号x分量的频谱图.结果表明,不同震源时间函数激发的震电波场在频率域的响应呈现相似的整体特征,但在频谱细节方面存在一定差异,并且在相同的地震矩情况下,震电波场频谱的幅值变化明显,其中Ricker子波幅值最大,产生的电磁场能量最强.
|
图 8 震源时间函数为Ricker子波、梯形函数、指数函数和Herrmann函数对应的(a)地震ux,(b)电场Ex,(c)磁场Hx的频谱示意图 Fig. 8 Frequency spectrum of (a) ux, (b) Ex, and (c) Hx induced by source time function Ricker wavelet, trapezoid function, exponent function and Herrmann function |
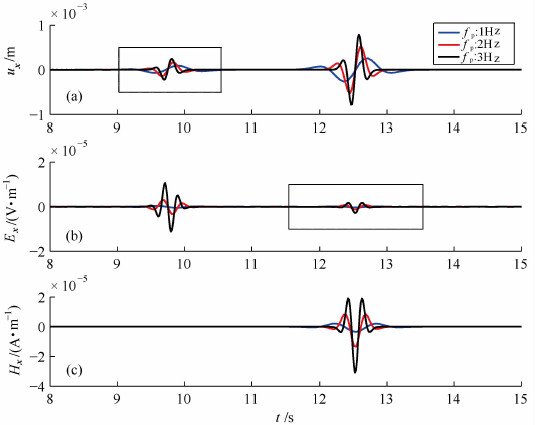
本小节重点考虑不同频率激发的地震电磁信号的时域和频域响应.上一小节的结果表明Ricker子波也能从整体上反映震电波场的主要特征,而且Ricker子波便于对频率进行定量分析,因此,本文以Ricker子波为例来考察震电波场对源的频率响应特征.图 9给出了均匀全空间峰值频率分别为1,2,3 Hz的Ricker子波激发的同震电磁信号.为清晰地显示图形中较弱的信号,对位移场P波所在的9~10.5 s(图 9a方框部分)和S波产生的电场信号所属的11.5~13.5 s(图 9b方框部分)分别进行了10倍的局部放大.可以看到:在某一频率范围内,地震波随着频率的增大而显著增强;伴随P波和S波的电磁信号变化规律与地震波相似,峰值频率越大,幅值越大,能量越集中(图 9(b,c));不同频率产生的同震电磁信号在相位和到达时间上保持一致.
|
图 9 均匀全空间峰值频率分别为1 Hz、2 Hz和3 Hz的Ricker子波激发的(a)地震ux,(b)电场Ex,(c)磁场Hx示意图(图示中方框部分放大了10倍) Fig. 9 (a)ux, (b)Ex, (c)Hx due to the models with Ricker wavelet of 1 Hz, 2 Hz, and 3 Hz peak frequencies in a homogenous full space.The relative weak signals in the solid square have been amplified by a factor of 10 for clear presentation |
本研究基于天然地震频段,重点探讨了双力偶点源以及有限断层面源在不同的模型中所产生的震电波场的基本特征及可能存在的差异.数值模拟得到的地震波和电磁场在波形和频谱方面具有较好的一致性和相关性.虽然前人研究很少涉及频谱的讨论,本文得到的频谱方面的相关认识尚有待更多理论模拟和实测资料的检验,但本文得到的波形的到时一致性这一特征与前人的研究结果相吻合,实际的野外同震电磁观测结果也发现波场具有到时一致性的特征.全空间中伴随P波以及S波都存在电场信号,但是S波激发同震电场信号的能力在一般情况下远弱于P波激发同震电场信号的能力.在半空间中由于自由界面的存在,Sv-P转换波激发的同震电场信号与伴随S波到达的同震电场信号叠加在一起,其幅值相比全空间模型显著增强.
不同模型结构的研究结果显示,两层介质模型由于自由表面和介质层间分界面的存在,产生了伴随反射波和多次波传播的电磁信号,故其波形较半空间模型更为复杂,持续时间更长,同时由于地震波在界面处发生反射,使得能量衰减,导致最终到达接收点的地震电磁信号有所减弱.总体而言,地震电磁信号的波形、振幅和持续时间等都不同程度受到模型结构的影响,结构越复杂,波形也越复杂.
对于有限断层面源和双力偶点源,前者可以视为断层面内的许多双力偶点源的叠加,有限断层面源的地震矩能量是随着破裂传播过程缓慢释放的,而双力偶点源的地震矩能量是同时释放的,所以有限断层面源产生的地震电磁信号的波型更复杂,持续时间也更长.
为了考察不同类型震源时间函数对地震和电磁波场的影响,我们分别选择了Ricker子波、梯形函数、指数函数和Herrmann函数4种模型进行了数值模拟,结果表明这4种不同模型激发的震电波场在波形和频谱响应方面整体上呈现相似的特征,但在波形和频谱的细节方面存在一定差异,其中,Ricker子波产生的信号幅值最大,波形和频谱结构相对简单、清晰.需要说明的是,虽然Ricker子波与地震的实际震源时间函数存在一定的差异,但其得到的结果既相对简单、清晰,又能反映波场的整体特征而不失一般性,并且可以方便地考察结果的频率响应,所以,本文以Ricker子波为例对波场的频率响应进行了探讨,获得了以下初步认识,不同的Ricker子波峰值频率会导致震电波场幅值的差异,但对信号的相位和到达时间并不产生显著的影响.当然,由于该认识并无前人结果可以借鉴,其适用性尚有待更多数值模拟和实测资料的检验.
为了能更好地突出不同模型参数对震电波场的影响,本文选择相对简单的模型,分别对全空间、半空间和两层介质等模型结构以及不同激发源(震源时间函数类型、Ricker子波峰值频率)模型进行了研究,获得了震电波场的初步认识.考虑到实际地球介质结构和震源模型可能比本研究采纳的简化模型更为复杂,今后有必要选择更接近实际的模型进一步进行系统的数值模拟研究,为实际震电观测资料的解释提供理论依据.
附录A对于均匀孔隙介质,频率域的震电控制方程组可表示如下(参见Pride[7]):
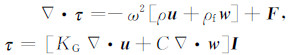
|
(A1) |
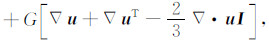
|
(A2) |

|
(A3) |
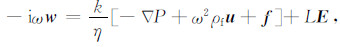
|
(A4) |
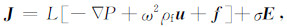
|
(A5) |
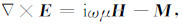
|
(A6) |
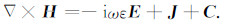
|
(A7) |
该方程组本质上是Biot孔隙介质理论和Maxwell方程组的结合,其中E和H分别为电场和磁场,u和w分别为固体位移和流体渗滤位移,τ表示应力张量,P表示流体压力,F和f分别为介质体力和作用在流体相上的压力,ρ和ρf分别代表介质平均密度和孔隙流体密度,L为随频率变化的动电耦合系数,J表示电流密度,C和M分别表示外加的电流源和磁流源,KG为Gassmann体积模量,G为固体骨架剪切模量,KG与固体体积模量Ks、流体体积模量Kf和排除流体后骨架的体积模量Kfr具有如下的关系:
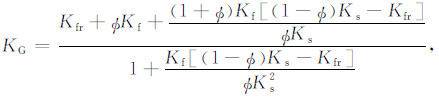
|
(A8) |
其中Φ为介质的孔隙度.
附录B对于底层为半无限空间的N+1层层状介质模型,第j(1≤j≤N)层的边界记为z=z(j-1)和z=z(j),顶层可以是半空间,也可以是一厚度有限的层(此时将其自由表面记为z=z(0)),假设源位于第s层并且2≤s≤N,即源不在最顶层也不在最底层.
在z轴垂直向下的柱坐标下,用一套基函数(见Ren等[23]的附录A)分解震电控制方程中所有的矢量和标量,得到两套方程组,分别对应于SHTE模式和PSVTM模式,他们都可以写成如下的形式:
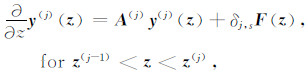
|
(B1) |
其中,A(j)代表第j层介质物性参数所控制的系数矩阵,F为外加的力源项(其具体表达式可参考Ren等[23]的附录B),对于SHTE模式和PSVTM模式,分别有
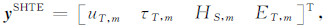
|
(B2) |
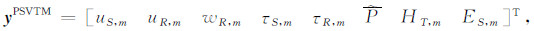
|
(B3) |
同时对于电磁场垂直分量,有
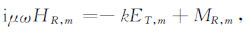
|
(B4) |
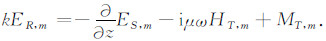
|
(B5) |
感谢审稿人提出的建设性的建议和意见.
| [1] | Matsushima M, Honkura Y, Oshiman N, et al. Seismoelectromagnetic effect associated with the İzmit earthquake and its aftershocks. Bull. Seism. Soc. Am. , 2002, 92: 350-360. DOI:10.1785/0120000807 |
| [2] | Karakelian D, Beroza G C, Klemperer S L, et al. Analysis of ultralow-frequency electromagnetic field measurements associated with the 1999 M7.1 Hector Mine, California, earthquake sequence. Bull. Seism. Soc. Am. , 2002, 92: 1513-1524. DOI:10.1785/0120000919 |
| [3] | 汤吉, 詹艳, 王立凤, 等. 5月12日汶川8.0级地震强余震观测的电磁同震效应. 地震地质 , 2008, 30(3): 739–745. Tang J, Zhan Y, Wang L F, et al. Coseismic signal associated with aftershock of the Ms8.0 Wenchuan earthquake. Seismology and Geology (in Chinese) , 2008, 30(3): 739-745. |
| [4] | 汤吉, 詹艳, 王立凤, 等. 汶川地震强余震的电磁同震效应. 地球物理学报 , 2010, 53(3): 526–534. Tang J, Zhan Y, Wang L F, et al. Electromagnetic coseismic effect associated with aftershock of Wenchuan Ms8.0 earthquake. Chinese J. Geophys. (in Chinese) , 2010, 53(3): 526-534. |
| [5] | Ivanov A G. Effect of electrization of earth layers by elastic waves passing through them. Dokl. Akad. Nauk. SSSR , 1939, 24: 42-45. |
| [6] | Frenkel J. On the theory of seismic and seismoelectric phenomena in a moist soil. J. Eng. Mech. , 1944, 8(4): 230-241. |
| [7] | Pride S R. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B , 1994, 50: 15678-15696. DOI:10.1103/PhysRevB.50.15678 |
| [8] | Haartsen M W, Pride S R. Electroseismic waves from point sources in layered media. J. Geophys. Res. , 1997, 102: 24745-24769. DOI:10.1029/97JB02936 |
| [9] | Garambois S, Dietrich M. Full waveform numerical simulations of seismoelectromagnetic wave conversions in fluid-saturated stratified porous media. J. Geophys. Res. , 2002, 107: 40-58. |
| [10] | Chen X F. Seismogram synthesis in multi-layered half-space part I.Theoretical formulations. Earthquake Research in China , 1999, 13: 149-174. |
| [11] | Ge Z X, Chen X F. Wave propagation in irregularly layered elastic models: A boundary element approach with a global reflection/transmission matrix propagator. Bull. Seism. Soc. Am. , 2007, 97(3): 1025-1031. DOI:10.1785/0120060216 |
| [12] | Ren H X, Huang Q H, Chen X F. A new numerical technique for simulating the coupled seismic and electromagnetic waves in layered porous media. Earthq. Sci. , 2010, 23: 167-176. DOI:10.1007/s11589-009-0071-9 |
| [13] | Ren H, Huang Q H, Chen X. Analytical regularization of the high-frequency instability problem in numerical simulation of seismoelectric wave-fields in multi-layered porous media. Chinese J. Geophys. , 2010(b), 53: 506-511. |
| [14] | Martner S T, Sparks N R. The electroseismic effect. Geophys. , 1959, 24: 297-308. DOI:10.1190/1.1438585 |
| [15] | Thompson A H, Gist G A. Geophysical applications of electrokinetic conversion. Leading Edge , 1993, 12: 1169-1173. DOI:10.1190/1.1436931 |
| [16] | Thompson A H, Hornbostel S, Burns J, et al. Field tests of electroseismic hydrocarbon detection. Geophys. , 2007, 72: N1-N9. |
| [17] | Zhu Z, Cheng C H, Toksöz M N. Electro-kinetic conversion in a fluid-saturated porous rock sample. SEG Technical Program Expanded Abstracts, 1994, 1057-1060. |
| [18] | Zhu Z, Haartsen M W, Toksöz M N. Experimental studies of electrokinetic conversions in fluid-saturated borehole models. Geophys. , 1999, 64: 1349-1356. DOI:10.1190/1.1444639 |
| [19] | Zhu Z, Haartsen M W, Toksöz M N. Experimental studies of seismoelectric conversions in fluid-saturated porous media. J. Geophys. Res. , 2000, 105: 28055-28064. DOI:10.1029/2000JB900341 |
| [20] | Huang Q H. Rethinking earthquake-related DC-ULF electromagnetic phenomena: towards a physics-based approach. Nat.Haiards Earth Syse.Sci. , 2011, 11(11): 2941-2949. DOI:10.5194/nhess-11-2941-2011 |
| [21] | Gao Y H, Hu H S. Seismoelectromagnetic waves radiated by a double couple source in a saturated medium. Geophys. J. Int. , 2010, 181: 873-896. |
| [22] | Hu H S, Gao Y X. Electromagnetic field generated by a finite fault due to electrokinetic effect. J. Geophys. Res. , 2011, 116. |
| [23] | Ren H X, Chen X F, Huang Q H. Numerical simulation of coseismic electromagnetic fields associated with seismic waves due to finite faulting in porous media. Geophys. J. Int. , 2012, 188: 925-944. DOI:10.1111/gji.2012.188.issue-3 |
| [24] | Gao Y X, Chen X F, Hu H S, et al. Early electromagnetic waves from earthquake rupturing: I.theoretical formulations. Geophys. J. Int. , 2013, 192: 1288-1307. DOI:10.1093/gji/ggs096 |
| [25] | Gao Y X, Chen X F, Hu H S, et al. Early electromagnetic waves from earthquake rupturing: II. validation and numerical experiments. Geophys. J. Int. , 2013, 192: 1308-1323. DOI:10.1093/gji/ggs097 |
| [26] | Bouchon M. A simple method to calculate Green's functions for elastic layered media. Bull. Seism. Soc. Am. , 1981, 71: 959-971. |
| [27] | Herrmann R B. SH-wave generation by dislocation source-a numerical study. Bull. Seism. Soc. Am. , 1979, 69: 1-15. |
 2013, Vol. 56
2013, Vol. 56