2. 地理信息工程国家重点实验室, 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
海洋中有一些热点火山山脉,分布在各大洋中,它们是岩石圈板块运动到地幔内火山源上方时生成的,由地幔深处上升流提供岩浆,以岩浆库的形式保存在这些火山下面,形成活火山,它们的轨迹就是火山山脉,这样的火山源就是热点.当岩石圈板块运动到热点上部时,便形成了火山中心;随着板块不停地移动跨过热点,先形成的火山即移出了热点,火山也逐渐熄灭成为死火山,在后面热点处又形成了新的火山.由于热点是固定于下地幔的,因此板块相对于热点的运动,便是相对于下地幔的运动.热点参考基准就是相对于下地幔固定的参考基准,具有明确的地球物理意义,所以基于热点参考架的绝对板块运动模型被不少地球物理学者采用.
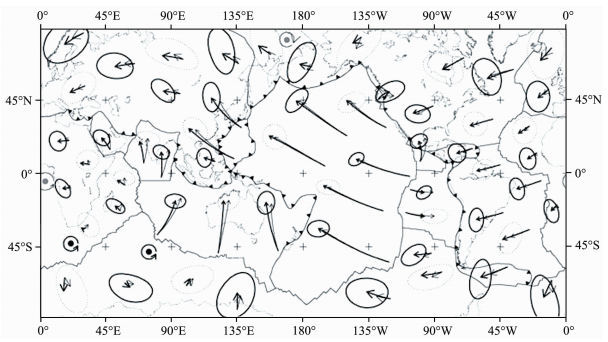
基于热点参考架的第一个绝对板块运动模型AM1,是Minster和Jordon[1]利用热点的走向数据(trend)建立的;Chase[2]利用热点数据由相对运动模型P071推导出了绝对板块运动模型P073.随着热点观测数据的增多,同时利用热点的火山海岭走向数据(trend)和热点速率(rate)建立热点参考基准便成为一种趋势,比如模型AM1-2[3]、HS2-NUVEL1[4]和HS3-NUVEL1A[5]等.AM1-2模型曾被用于卫星激光测距数据的分析中,而建立HS2-NUVEL1模型时所用的热点数据与建立AM1-2时利用的是同样的数据组,即5个热点速率和9个热点走向数据,分别分布在太平洋板块、可可斯板块、纳兹卡板块和北美板块,所以HS2-NUVEL1相对于热点的运动速度大体上与AM1-2的相应值接近,两者的差别可能主要在于相对运动模型NUVE L-1与RM2的区别[4, 6].HS3-NUVEL1A模型是由太平洋地区年轻(0~5.8 Ma)热点火山链的2个热点速率和11个热点走向数据约束于相对运动模型NUVE L-1A而建立的,该模型给出了15个板块相对于热点的运动速度.热点之间没有很大的相对运动,但是在95%置信范围内,相对运动速度在20km/Ma到40km/Ma之间,有的甚至达到±145km/Ma的范围.相对于HS3-NUVEL1A的板块运动速度的不确定度要比相对于HS2-NUVEL1的小.HS2-NUVEL1的14个欧拉矢量中有9个位于HS3-NUVEL1A的95%置信区域之外;而HS3-NUVEL1A的14个欧拉矢量全部位于HS2-NUVEL1的95%置信区域之内.相对于HS2-NUVEL1基准,太平洋板块的角速度矢量位于HS3-NUVEL1A中太平洋板块的95%置信区域之内,但在0~3Ma期间,Wessel和Kroenke[7]估计的太平洋板块的角速度要远远位于置信区间之外.相对于HS3-NUVEL1A基准,太平洋板块的角速度矢量在速率上不同于47 Ma前的平均值,但在方向上大致相同;在夏威夷-皇帝岭火山链上太平洋板块现今的旋转速率1.06±0.10°/Ma要比47 Ma年的平均值0.70°/Ma快50%[5].图 1显示的就是板块分别相对于热点参考架HS3-NUVEL1A和HS2-NUVEL1的运动速度,其中粗箭头表示的是在HS3-NUVEL1A中相对于热点参考架的板块运动速度,细箭头表示的是在HS2-NUVEL1中板块相对于热点参考架的运动速度.在HS3-NUVEL1A中,太平洋板块的运动速度要比HS2-NUVEL1中的快8~9km/Ma,且向西偏北方向运动[5];HS3-NUVEL1A与HS2-NUVEL1相对于热点的板块角速度之间的矢量差随着板块的不同而变化,最大的矢量差(0.17°/Ma)是可可斯板块;最小的矢量差是0.08°/Ma,位于太平洋板块(见图 1和表 1).
|
图 1 板块相对于热点参考架HS2-NUVEL1和HS3-NUVEL1A的运动速度[5] Fig. 1 Plate motion relative to HS2-NUVEL1 and HS3-NUVEL1 Amodel [5] |
国内部分学者在热点和热点参考框架方面也做了不少工作.孙付平[6]分析了Wilson-Morgan的热点假说,讨论了基于同一数据组的两个参考基准HS2-NUVEL1和AM1-2的区别和联系,并针对热点参考架和岩石圈无整体旋转参考架中可能存在的问题,提出了自己的模型,即太平洋海岭固定参考架PRF-NUVEL1,分析了该参考架的合理性和可行性.Wang等[8]在研究中发现,前人广泛采用的板块相对于热点的速度模型HS2-NUVEL1与太平洋区域以外的热点观测数据不符合,于是利用NUVEL-1A模型给出的板块相对运动,通过拟合分布于7个板块上的22个热点火山方向的数据,得到了一个新的板块绝对运动模型T22A模型.该模型不但能比HS2-NUVEL1模型更好地拟合全球热点数据,而且反映出热点起源的下地幔物质在进行与岩石圈板块方向相反的运动,下地幔速度约为板块速度的1/4.这一结果否定了过去20多年来广泛采用的热点固定假设,推论所得地幔黏度结构与从冰后回弹等数据反演得到的结果也非常符合,因而对研究地幔对流、重建古板块运动、分析真极移与全球参考系都有极为重要的意义.金双根等[9]根据Minster和Jordan提供的热点观测值和估计值,利用ITRF2000VEL模型中板块相对运动的欧拉矢量,推导出了基于热点的绝对板块运动模型HS2-ITRF2000,但HS2-ITRF2000模型并未反映相邻大西洋岩石圈受大西洋中脊扩张的影响,且热点数据不准确,尤其速率误差较大,热点间还存在相对运动等,因此该模型还不能完全精确代表板块的绝对运动.魏子卿[10]利用一组近来(0~7.8 Ma)全球分布的热点的迁移速率和走向数据,结合板块运动模型NNR-NUVEL1A,建立了现今绝对板块运动模型APM2,该模型表明,岩石圈相对深部地幔有一个以49.423°S、90.625°E为极,速率为0.1983°±0.0135°/Ma的净旋转;模型还表明太平洋热点同印度-大西洋热点不一致,显示太平洋热点的运动也不一致.同时,文献[10]还表明,同一个板块的运动速度和运动方向在不同的模型里是不同的.比如,对于欧亚板块来说,一些模型给出是顺时针的旋转,另外一些模型则相反,非洲板块和其他一些板块也有这种状况发生.或许这与不同的作者利用热点数据有关.如果热点之间是相对固定的,并且相对板块运动模型是正确的,热点位于一个独立的板块足够确定绝对板块运动.然而,实际上热点相对于彼此不是固定的.
对于热点参考框架,可能存在以下两个方面的问题:(1)热点数据尚不准确;(2)热点之间存在着相对运动.相对于下地幔热点是否是稳定的,目前还没有统一的结论.Molnar和Stock[11]认为,太平洋与大西洋的热点之间存在着量级1cm/a左右的沿东偏南方向的相对运动;不过,Steinberger[12]认为热点之间的相对运动比板块之间的相对运动要小得多,于是热点经常被用作定义板块运动的参考框架;Divenere和Kent[13]专门讨论了太平洋和印度洋-大西洋上的热点的固定性,认为夏威夷-皇帝岭和印度洋-大西洋热点之间也存在着相对运动,量级大约在2.5cm/a;Gripp和Gordon[4]在建立HS3-NUVEL1A模型时也分析了这个问题,认为热点之间没有很大的相对运动,但是在95%置信范围内,相对运动速度在2~4cm/a之间;Tarduno等[14]认为夏威夷热点在81~47 Ma间曾经以超过4cm/a的速度移动;Wang等[15]也认为,在过去的40 Ma期间,热点是呈系统移动状态的.魏子卿[10]也认为太平洋板块上的热点与印度洋-大西洋上的热点不一致,表明太平洋热点的运动也不一致.然而,就目前科学技术和观测手段的发展水平来说,即使热点参考基准只是一个近似固定的基准,也迫使我们支持它去量测板块的绝对运动.我们相信,热点的不固定性将不会影响给出的结论.所以,我们依然选择热点参考框架作为基本的参考框架[10].
鉴于此,本文提出建立平均热点参考基准(Medial-HotSpotReferenceDatum,简称MHS基准)的思想.即选择尽可能多的热点速率和走向数据,建立一个准则,扣除热点之间的平均相对运动,以热点相对于下地幔的总体运动最小为准则,建立基于平均热点的参考基准.以板块相对于热点的比较新的运动数据作为约束,分别以地学板块运动模型NUVE L-1A和实测模型为基础,建立基于平均热点参考基准的地学模型MHS-NUVEL1A和实测绝对板块运动模型MHS-ITRF2005,比较两个模型的差异并分析原因.最后讨论并比较了岩石圈的西向漂移,给出了岩石圈相对于下地幔整体旋转(漂移)的更精确的定量估计.
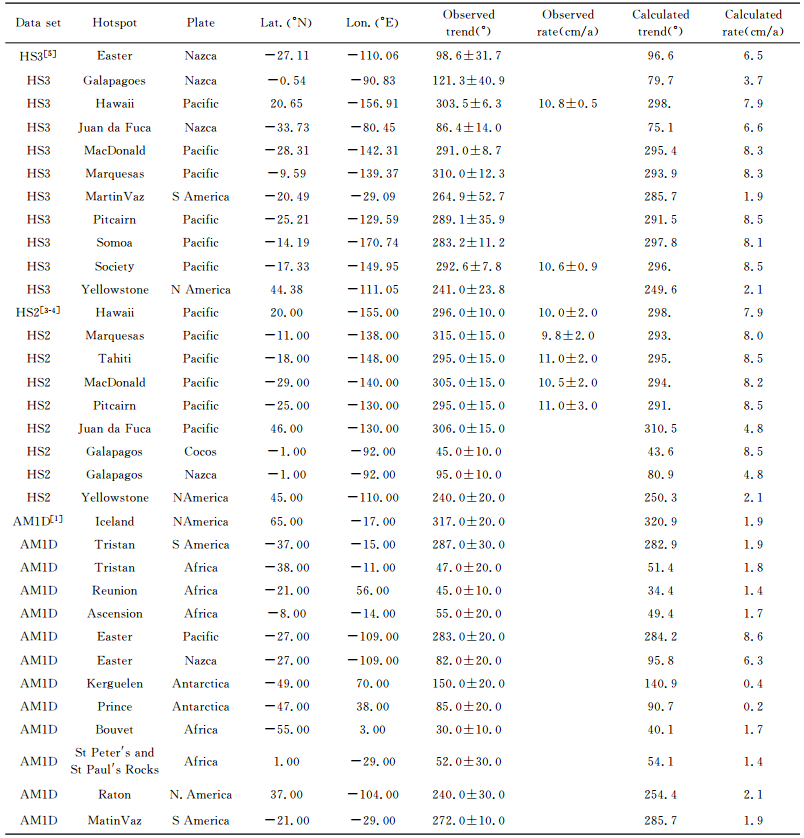
2 数据表 1给出了建立各种热点模型时用到的数据组,其中,HS3指的是来自Gripp和Gordon[5]所用到的11个走向数据和2个速率数据,来自太平洋区域0~5.8 Ma年轻的火山链;HS2数据组指的是同样来自太平洋区域,但时间跨度要比HS3的数据组晚,即0~10 Ma火山活动的数据,在Gripp和Gordon[4]所建模型HS2-NUVEL1和Minster和Jordan[3]中所建模型AM1-2中都用到的9个走向数据和5个速率数据;AM1D指的是Minster等[1]所用到的13个走向数据,来自不同的板块,时间跨度大致约束于过去的40 Ma的火山活动.本文建立模型即采用这些观测数据,共包含有33个走向数据和11个速率数据,时间跨度取为0~40 Ma的火山活动.
热点运动的速率和趋势在不同方面影响着板块的绝对运动.热点速率对于板块的运动速度比较敏感,但是热点走向就对板块的运动方向敏感,当然,同时利用热点的速率和趋势比单独利用任一种数据要好[10].
3 方法根据板块运动理论,每个板块服从欧拉定律,即Vi=Ω ×ri.如果已知板块上的运动速度或其它的运动数据,即可反演该板块的欧拉矢量.反演欧拉矢量的方法为:(1)假定已知全球相对板块运动模型(如NUVE L-1A);(2)求任一个板块(通常是太平洋板块)相对热点的欧拉矢量;(3)将该板块的绝对运动加其余板块对该板块的相对运动,即得基于热点的全球绝对板块运动[6, 10].
利用这种思路,就可以建立基于热点的绝对板块运动模型.这里我们提出建立平均热点参考基准的准则.经上述众多研究者证实,热点之间虽有相对运动,但平均运动速度不会超过2cm/a,比如,印度洋的热点运动速度仅为1cm/a,太平洋、大西洋热点间的运动速度为3cm/a;而板块的运动速度一般为2~10cm/a.从太平洋板块上热点速率的观测值即表 1中的数据可以看出,热点火山链的运动速率数据的误差也在2~3cm/a之间,所以,利用热点作为绝对板块运动的基准点是可行的.Wang等[8]在研究中发现,热点起源的下地幔物质在进行与岩石圈板块方向相反的运动,下地幔速度约为板块运动速度的1/4.以此为基础,建立平均热点参考基准的约束准则.由表 1中的热点数据可知,只有位于太平洋板块的热点有其运动速率数据,那么取其1/4作为约束准则,将位于太平洋板块的热点速率均约束于该准则,因热点在做与板块方向相反的运动[8],所以约束准则即是将热点速率扣除热点所在板块平均运动速率的1/4.将经过该准则约束之后的热点数据再参与热点运动模型的建立和解算,即参与下面的步骤.
数据整理好之后,基于上述思路建立热点参考基准的观测模型.假设板块的欧拉矢量的分量为(ωx,ωy,ωz),地球上任一点的位置矢量的分量为(r,ϕ,λ).由于地球表面任一点的相对运动速度总是正切于球面,故其速度矢量可用纬向分量Vn和经向分量Ve来表示(如图 2所示),则:
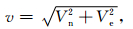
|
(1) |
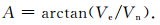
|
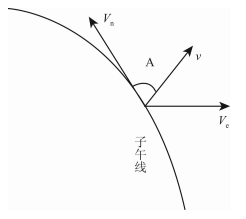
(2) |
|
图 2 台站速度分量示意图 Fig. 2 Weight of site velocity |
其中,
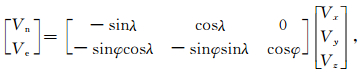
|
(3) |
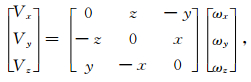
|
(4) |
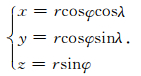
|
(5) |
对于上述模型的解算,利用迭代加权的最小二乘方法,通过使χ2,即
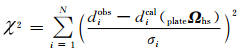
|
(6) |
为最小,再利用表 1中的观测数据,即可反演出每个板块相对热点的欧拉矢量.(6)式中diobs是第i个热点的观测数据,因目前太平洋板块的平均运动速率大致在6cm/a(在日本九洲附近为3~4cm/a,在日本-汤加海沟一带达到最大9cm/a[16]),所以如果观测数据diobs取热点速率时,要扣除太平洋板块平均运动速率的1/4之后再参与下面的解算;dical是第i个观测数据的模型估计值,即公式(1)和(2)中需要确定的运动速率v或方位角A,σi是第i个数据的中误差,N是热点数据的总个数.模型估计值dcal i的大小由欧拉矢量(plateΩhs)决定,即某个板块相对于热点角速度的欧拉矢量.由于板块之间的运动被约束到与某个相对板块运动模型(比如地学模型NUVE L-1A)一致,因而反演时只需平差某一个板块的欧拉矢量,再由该板块的相对运动模型导出另一个绝对板块运动模型[6, 10, 17].
根据表 1列出的热点数据,利用上述方法和约束准则,分别以地学模型NUVE L-1A[18]和实测模型ITRF2005VEL[19]为基础,建立基于平均热点参考架的地学绝对板块运动模型MHS-NUVEL1A和实测绝对板块运动模型MHS-ITRF2005,并与其它基于热点的绝对板块运动模型进行比较和分析.
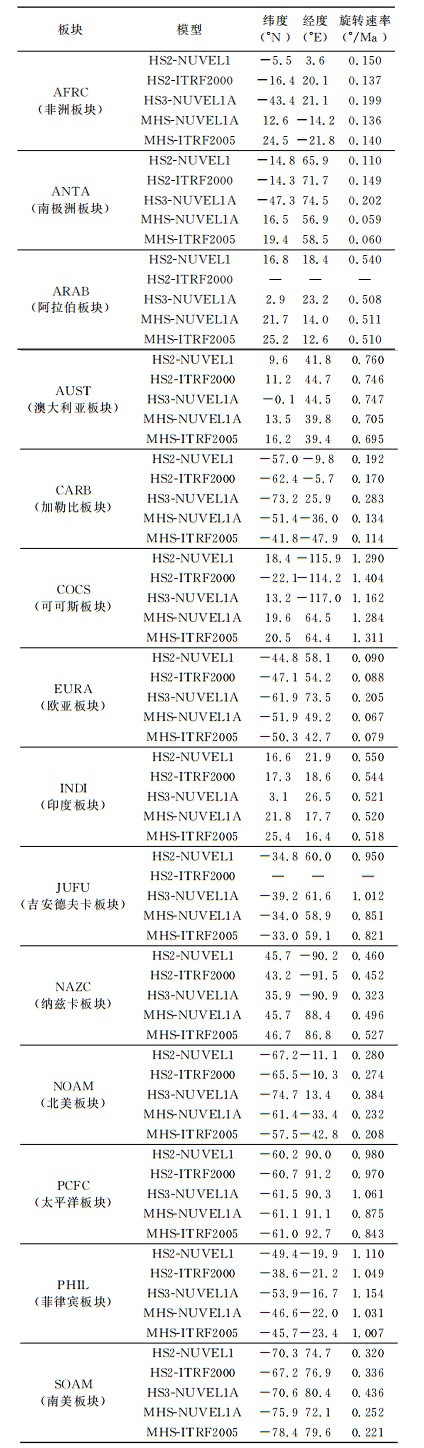
4 结果及分析表 2给出了几种基于热点的绝对板块运动模型的比较,其中HS2-NUVEL1模型来自于Gripp和Gordon[4];HS2-ITRF2000[9]是金双根等利用建立HS2-NUVEL1模型时的热点数据,构建的基于实测板块运动模型ITRF2000VEL的热点绝对板块运动模型;HS3-NUVEL1A[5]模型是以地学板块运动模型NUVE L-1A为基础,利用11个走向数据和2个速率数据建立的基于热点参考架的地学绝对板块运动模型;MHS-NUVEL1A和MHS-ITRF2005模型分别是笔者以地学模型NUVE L-1A和实测模型ITRF2005VEL为基础,利用33个方位角(走向)数据和11个速率数据建立的基于平均热点参考架的绝对板块运动模型.
|
|
表 2 基于热点参考架的绝对板块运动模型的比较 Table 2 Comparison of several absolute plate motion models based on hotspot reference frame |
由于HS2-ITRF2000和HS2-NUVEL1两个模型所用的热点数据是一样的,区别就在于ITRF2000VEL与NUVE L-1的差别.从整体上来看,这两个模型所估计的AUST、PHIL、NAZC和PCFC等板块的绝对欧拉矢量比较接近,而NOAM、SOAM、AFRC和EURA板块的绝对欧拉矢量相差较大,甚至方向发生变化[9].
同样,MHS-ITRF2005和MHS-NUVEL1A也是基于同样的热点数据得到的,则两者主要区别即为ITRF2005VEL和NUVE L-1A模型的区别.整体上这两个模型有较好的一致性,大多数板块的欧拉极和旋转速率差别不大,个别板块有所差异,比如CARB板块,两个模型所估计的欧拉极和旋转速率都有些差别,尤其欧拉极位置的绝对值相差10°左右.
而HS3-NUVEL1A和MHS-NUVEL1A两个基于热点的绝对板块运动模型的区别在于所采用的热点数据不一样,但两模型的约束准则大致是一样的,即都是将各自的热点数据求逆,同时使相对运动速度与NUVE L-1A模型相等来求得的.从整体上来看,这两个模型有较大的差别,HS3-NUVEL1A模型的旋转速率普遍高于MHS-NUVEL1A模型:AUST、INDI和PHIL、JUFU、PCFC等板块的旋转速率相差不大,在2%~17%;AFRC、CARB、NOAM和SOAM的旋转速率在两个模型中的差别达到30%~50%;只有NAZC板块在MHS-NUVEL1A模型的旋转速率高于HS3-NUVEL1A模型35%左右,COCS板块在10%左右,ARAB板块在6%左右.
另外,平均热点参考基准MHS-ITRF2005和MHS-NUVEL1A相比于HS2-ITRF2000、HS2-NUVEL1两个模型,除了约束准则不一样,最大的差别在于平均热点模型采用的热点速率和走向数据都比HS2要多.热点速率对于板块的运动速度比较敏感,但是热点走向就对板块的运动方向比较敏感. MHS-ITRF2005和MHS-NUVEL1A比HS2-ITRF2000和HS2-NUVEL1采用了更多的热点走向数据,因此,有些板块欧拉极的位置在上述模型的比较中差别比较大,比如AFRC板块欧拉极的大小和方向在MHS基准和HS2基准中差别比较明显,NAZC经度方向相反,ANTA纬度方向相反,NOAM和CARB欧拉极位置中的经度差别较大等等.总之,热点走向数据对板块运动的欧拉极位置约束比较明显.
经上述结果发现,热点数据在构建基于热点的参考基准时发挥着至关重要的作用,即热点参考基准是由热点来决定的[10].因此,收集并整理更全面、更高精度的热点数据是很重要的一步工作,同时,还要剔除观测误差比较大的热点,并对热点数据进行分析和处理,对存有相互运动的热点采取一定的准则进行约束,如此建立的热点参考基准才能说具有一定的可靠性.
5 岩石圈的西向漂移由上述结果和分析发现,通过反演热点数据而建立的绝对板块运动模型,其精度取决于所选用的相对板块运动模型,而相对板块运动模型的建立通常是依据无整体旋转(NNR-nonetrotation)准则,但是,无整体旋转基准本身相对于平均中圈并不是固定的,而是相对于岩石圈存在着整体旋转,这种较差旋转也称为岩石圈的漂移.漂移的量级可以根据板块的受力模型来计算,亦可以由热点的实测数据和板块的运动模型给出岩石圈相对于下地幔整体旋转的更精确的定量估计[6, 10, 17].
假设某一个板块在热点参考基准中的角速度矢量为ωh,板块在无整体旋转基准中的角速度矢量为ωn,岩石圈相对于热点参考基准漂移的速度矢量为ωnr,那么这三者之间的关系为
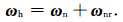
|
(7) |
利用(7)式即可求出岩石圈相对于热点参考基准的整体旋转,表 3给出了几种模型计算的岩石圈的漂移与观测值的比较.其中,Solomon和Sleep [20]采用两种板块的受力模型给出岩石圈的整体旋转:其一,由所有对板块运动的阻力都集中于大陆之下的模型给出的整体旋转为0.2°/Ma,旋转极为54°S,100°E;其二,由消减板舌对水平板块施加一纯力矩的模型,给出了一个旋转极沿4°S,52°E,速率为0.14°/Ma的岩石圈整体旋转;Harper[21]的模型特征与Solomon和Sleep的第二种方案相同,即都是采用的去除板块大陆之下的附加拖曳力的纯力矩模型,其给出的岩石圈的整体旋转的位置接近于Argus和Gordon[18]给出的观测值,但旋转速率仍慢约30%;而地学模型HS3-NUVEL1A给出的岩石圈漂移的的位置在(56°S,70°E),其速率为0.44±0.11°/Ma,比模型HS2-NUVEL1的整体旋转快了25%[5].
|
|
表 3 各种模型得到的岩石圈整体旋转的比较 Table 3 Comparison with the net rotation of the lithosphere in several models |
由地学模型MHS-NUVEL1A可知,NNR-NUVEL1A有一个旋转速率为0.2221°/Ma、旋转极在(48.7°S,62.7°E)的旋转,即表明岩石圈也有一个相同大小相对于热点的整体旋转;这与Solomon和Sleep [20]采用第一种模型和Harper[21]由消减板舌对水平板块施加重力拖拉力矩的模型给出的岩石圈的整体旋转速率基本一致,旋转极的纬度也很接近,只有旋转极的经度相差有20°左右.
由实测的热点数据和ITRF2005的速度场给出了一个基于实测的热点参考架MHS-ITRF2005,它和无整体旋转参考架NNR-NUVEL1A之间的较差旋转速率为0.2554°/Ma,旋转极(49.8°S,61.7°E),这与Harper及Argus和Gordon给出的岩石圈的整体旋转的旋转极很接近,旋转速率比Harper的模型快了11.5%,比HS2-NUVEL1的整体旋转慢了21%.这似乎表明,由消减板舌对水平板块施加的重力拖拉力矩是板块的主要受力来源,同时,也印证了Richard[22]的观点:即大陆之下的附加拖曳力是导致热点参考架和NNR参考架之差的主要原因.当然,这个观点的正确与否,还需要更加精确的实测的热点数据和板块运动的数据来进行验证.
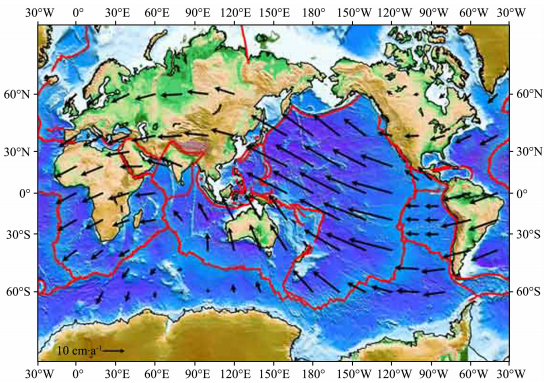
另外,对于岩石圈板块总体向西漂移的定向性有不少学者作过研究[4-5, 18, 23-24],由图 3可以看出,北半球岩石圈板块运动矢量相对热点参考基准都是向西漂移的,南半球除了印度洋、大西洋和非洲是向北运动外,太平洋和大西洋洋脊,虽然以向西两侧做离散运动为主,但洋脊西侧运动矢量明显大于东侧,因此,整体上仍然可以看作是向西漂移的.由于北半球较南半球向西漂移量较大,所以在赤道附近可能存在着一个南北半球相对扭转的现象.目前整个岩石圈相对地幔做向西的整体运动已得到普遍的承认[15].
|
图 3 相对于热点参考基准的现今板块运动速度示意图[24] Fig. 3 Present-day plate motions relative to Hotspot reference datum [24] |
考虑到热点的运动,笔者利用全球更加精化的热点数据,分别以地学模型NNR-NUVEL1A和实测模型ITRF2005VEL为基础,建立了基于平均热点参考架的绝对板块运动模型MHS-NUVEL1A和MHS-ITRF2005,并与其它基于热点的绝对板块运动模型进行了比较和分析;最后讨论了岩石圈的整体旋转,给出了岩石圈相对于下地幔整体旋转(漂移)的更精确的定量估计,即基于实测的热点参考架MHS-ITRF2005和地学模型NNR-NUVEL1A之间的整体旋转为0.26°/Ma,旋转极在(50°S,62°E),这与由板块的受力模型给出的岩石圈的整体旋转的旋转极很接近,旋转速率大致快了10%.
关于岩石圈的西向漂移和整体旋转有很多公开的基本问题,比如漂移的真实速度是多少、漂移和旋转又是如何产生的等等,而由于地幔对流对大尺度岩石圈形成的应力场作为面力将造成岩石圈本身的变形,这些问题是否与岩石圈内部的应力分布也有关系[25],都还需要更多的实测数据和更精确的模型来进行检验.随着人类的认知和空间观测技术的迅猛发展,我们有理由期望这些问题在将来都能够得到更好的解决.
由上述讨论发现,基于热点的参考基准得到的岩石圈整体旋转与地球物理学家根据板块受力模型计算的岩石圈整体旋转在量级和方向上都基本一致,说明平均热点参考基准可能更符合实际情况.如果把目前IERS推荐采用的NNR参考基准改为新的平均热点参考基准,由于两者存在较差旋转,用于维持地球参考架稳定的速度场将发生较大改变,台站位移速度变化可达22mm/a;此外地球自转参数序列也会发生显著改变.IERS之所以定义NNR参考基准作为地球参考架的水平运动基准,是因为观测台站位于地壳上,这样定义是内部自洽的,不会与以前的结果产生矛盾.如果改为新的平均热点参考基准,会导致地球自转参数序列不连续,地球参考架内部不自洽.所以,考虑到历史、现状及用户使用的方便,尽管新的平均热点参考基准可能更符合地球参考系的理论定义,但IERS目前仍然采用NNR参考基准作为水平地壳运动参考基准.因基于热点的参考基准能够更加真实的反映地幔对流的实际情况,研究地幔对流和板块运动的地球物理学家更倾向于采用热点参考基准,而大地测量学家则倾向于采用NNR参考基准.
致谢特别感谢Rice大学的RichardG.Gordon和Missouri大学的Shimin Wang提供的部分数据和资料以及对本文工作的指导,与之进行的学术探讨和交流使作者受益匪浅.
| [1] | Minster J B, Jordan T H, Molnar P, et al. Numerical modelling of instantaneous plate tectonics. Royal Astronomical Society Geophysical Journal , 1974, 36(3): 541-576. DOI:10.1111/j.1365-246X.1974.tb00613.x |
| [2] | Chase C G. Plate kinematics: The Americas, East Africa, and the rest of the world. Earth Planet Sci. Lett. , 1978, 37: 355-368. DOI:10.1016/0012-821X(78)90051-1 |
| [3] | Minster J B, Jordan T H. Present-day plate motions. J. Geophys. Res. , 1978, 83(B11): 5331-5354. DOI:10.1029/JB083iB11p05331 |
| [4] | Gripp A E, Gordon R G. Current plate velocities relative to the hotspots incorporating the NUVEL-1 global plate motion model. Geophys. Res. Lett. , 1990, 17(8): 1109-1112. DOI:10.1029/GL017i008p01109 |
| [5] | Gripp A E, Gordon R G. Young tracks of hotspots and current plate velocities. Geophysical Journal International , 2002, 150(2): 321-361. DOI:10.1046/j.1365-246X.2002.01627.x |
| [6] | 孙付平.基于空间技术的现代地壳运动研究[博士论文].上海:中国科学院上海天文台, 1994. Sun F P. Research of Current Crustal Motions Based Upon Space Geodetic Techniques[Ph.D.thesis] (in Chinese). Shanghai: Shanghai Observatory, Chinese Academy of Science, 1994. |
| [7] | Wessel P, Kroenke L. A geometric technique for relocating hotspots and refining absolute plate motions. Nature , 1997, 387(6631): 365-369. DOI:10.1038/387365a0 |
| [8] | Wang S M, Wang R. Current plate velocities relative to hotspots: Implications for hotspot motion, mantle viscosity and global reference frame. Earth and Planetary Science Letters , 2001, 189(3-4): 33-140. DOI:10.1016/S0012-821X(01)00351-X |
| [9] | 金双根, 朱文耀. 3种板块绝对运动模型的建立及其比较. 中国科学院上海天文台年刊 , 2002(23): 21–27. Jin S G, Zhu W Y. Comparison and establishment of three absolute plate motion models. Annals of Shanghai Observatory Academa Sinica (in Chinese) , 2002(23): 21-27. |
| [10] | 魏子卿. 现今绝对板块运动. 地球科学与环境学报 , 2009, 31(4): 331–343. Wei Z Q. Current absolute plate motions. Journal of Earth Sciences and Environment (in Chinese) , 2009, 31(4): 331-343. |
| [11] | Molnar P, Stock J. Relative motions of hotspots in the Pacific, Atlantic and Indian Oceans since late Cretaceous time. Nature , 1987, 327(6123): 587-591. DOI:10.1038/327587a0 |
| [12] | Steinberger B. Motion of Hotspots and Changes of the Earth Rotation Axis Caused by a Convecting Mantle. Harvard: Harvard University, 1996 . |
| [13] | Divenere V, Kent D V. Are the Pacific and Indo-Atlantic hotspots fixed? Testing the plate circuit through Antarctica. Earth and Planetary Science Letters , 1999, 170(1-2): 105-117. DOI:10.1016/S0012-821X(99)00096-5 |
| [14] | Tarduno J A, Ducan R A, Scholl D W, et al. The Emperor Seamounts: Southward motion of the Hawaiian hotspot plume in Earth's mantle. Science , 2003, 301(5636): 1064-1069. DOI:10.1126/science.1086442 |
| [15] | Wang S M, Liu M. Moving hotspots or reorganized plates. Geology , 2006, 34(6): 465-468. DOI:10.1130/G22236.1 |
| [16] | 板块运动.百度百科, 2012.http://baike.baidu.com/view/381613.htm) Plate motion.Baiduencyclopedia, 2012. |
| [17] | 朱新慧, 孙付平, 王刃.基于两种不同参考架的绝对板块运动研究//信息工程大学测绘学院第五届博士生学术论坛论文集.郑州:信息工程大学测绘学院, 2010: 85-89. Zhu X H, Sun F P, Wang R. Study on absolute plate motion based on different reference frame//5th Doctoral Proceedings of Surveying and Mapping Institute (in Chinese). Zhengzhou: Information and Engineering University, 2010: 85-89. |
| [18] | Argus D F, Gordon R G. No-Net-Rotation model of current plate velocities incorporating plate motion model NUVEL-1. Geophys. Res. Lett. , 1991, 18(11): 2039-2042. DOI:10.1029/91GL01532 |
| [19] | 朱新慧, 孙付平, 王刃. 基于ITRF2005的全球板块运动模型. 地球物理学进展 , 2009, 24(3): 859–865. Zhu X H, Sun F P, Wang R. Global plate motion models based on ITRF2005. Progress in Geophysics (in Chinese) , 2009, 24(3): 859-865. |
| [20] | Solomon S C, Sleep N H. Some simple physical models for absolute plate motions. J. Geophys. Res. , 1974, 79(17): 2557-2567. DOI:10.1029/JB079i017p02557 |
| [21] | Harper J F. Mantle flow and plate motions. Geophys. J. Roy. Astron. Soc. , 1986, 87(1): 155-171. DOI:10.1111/gji.1986.87.issue-1 |
| [22] | Richard Y, Doglioni C, Sbedini R. Differential rotation between lithosphere and mantle: a consequence of lateral mantle viscosity variations. J. Geophys. Res. , 1991, 96(B5): 8407-8415. DOI:10.1029/91JB00204 |
| [23] | DeMets C, Gordon R G, Argus D F, et al. Effect of recent revisions to the geomagnetic reversal time scale on estimates of current plate motions. Geophys. Res. Lett. , 1994, 21(20): 2191-2194. DOI:10.1029/94GL02118 |
| [24] | Cuffaro M, Doglioni C. Global kinematics in deep versus shallow hotspot reference frame. Geological Society of America Special Papers , 2007, 430: 359-374. |
| [25] | 王建, 叶正仁. 地幔对流对全球岩石圈应力产生与分布的作用. 地球物理学报 , 2005, 48(3): 584–590. Wang J, Ye Z R. Effects of mantle flow on generation and distribution of global lithospheric stress field. Chinese J. Geophys. (in Chinese) , 2005, 48(3): 584-590. |
 2013, Vol. 56
2013, Vol. 56