核磁共振法(Magnetic ResonanceSounding, MRS)是一种能够对地下水进行直接探测的地球物理方法[1-2].这种方法利用地下水中氢质子能够产生核磁共振效应的原理, 对地下水的含量和赋存状态进行探测[3].在浅地表介质中, 游离的氢质子主要存在于水分子中, 因此, 只要获得核磁共振信号, 即可证明地下水的存在.同时, 通过分析信号形态来判断地下水的赋存形式[4].
核磁共振方法自20世纪80年代被前苏联科学家应用于地下水探测领域中后, 已经在全球超过20个国家和地区开展了实际应用[5], 其中, 法、中、美等少数国家生产出了系列的商品化核磁共振找水仪器.这些探测仪器主要在地面上开展一维核磁共振测量, 线圈的铺设方式通常为单匝大回线[6-9].如法国IRIS公司研制的NUMIS系统和美国VISTA Clara公司研制的GMR系统均采用大边长(91 m或100m)单匝方形线圈进行测量.国内由吉林大学研制的JLMRS系列仪器主要利用边长为100m和150m单匝线圈开展探测.对于利用多匝线圈探测, 特别是利用多匝小型线圈探测, 目前取得的研究成果并不多. 2009年荣亮亮等人曾对多匝小回线线圈和单匝大回线线圈找水技术的异同进行了相关对比和论述[10]. 2011年南非的J. M. Greben等人借助GMR系统利用2 m直径50匝的线圈在地下进行了超前探测试验, 但是受试验条件限制, 未获得理想信号[11].
核磁共振找水方法通过线圈检测地下水信号, 不同样式线圈所能达到的信号响应差异很大, 决定了探测系统能否对地下水进行有效探测[12].接收线圈对核磁共振信号的响应主要取决于传递特性, 通常与绕制结构和线圈大小有关[13].各国在研制核磁共振探测系统时, 都关心着线圈传递特性与所获信号质量之间的关系.对于现有常用的大边长单匝线圈来说, 由于阻抗固定、绕制形式成熟, 其传递特性已经完全满足地面测量要求.但是, 对于多匝环形线圈, 特别是应用在限定空间下(如隧道、矿井中)的多匝小型线圈来说, 其绕制结构复杂, 阻抗参数多变, 线圈对信号的提取能力会发生很大变化[10, 14].因此, 在设计这种线圈时, 需要充分考虑线圈参数对传递特性的影响, 以保证探测系统能够有效获得核磁共振信号.目前, 尚未有公开文献进行过相关讨论.
基于此, 本文在给出多匝环形线圈核磁共振信号初始振幅计算结果和接收线圈传递特性一般计算方法的基础上, 着重讨论了线圈参数对传递特性的影响, 同时给出了传递系数的临界值.通过传递系数和其临界值的比较, 得出不同线圈对核磁共振信号检测的有效性.最后, 通过野外探测试验结果, 证明了本文的推论, 为限定空间下核磁共振接收线圈的研制提供了理论和设计依据.
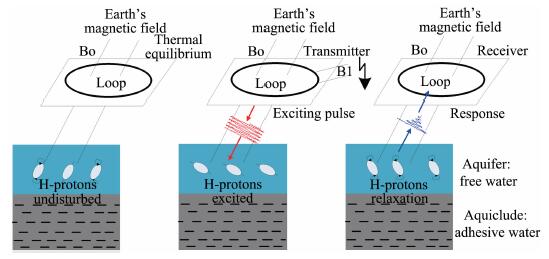
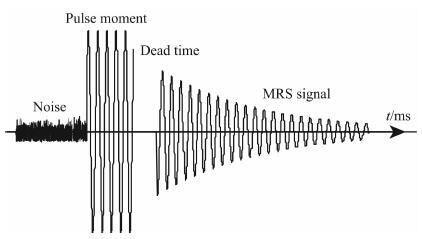
2 核磁共振信号的初始振幅在自然环境中, 地下水中的氢质子会以一定的频率环绕一条轴线进行旋进, 旋进频率与地磁场有关, 称为Larmor频率.当利用这个频率的能量对水中的氢质子进行激发时, 根据量子物理理论, 氢质子会向高能级跃迁.持续一段时间后撤去激发能量, 氢质子跃迁回低能级, 同时向外辐射能量.这个现象被称为核磁共振效应[12].在氢质子跃迁过程中, 释放的能量以磁信号的形式向外辐射, 此时, 根据电磁感应定律, 利用铺设在地面的线圈可以捕捉到这个信号, 并在线圈的两端以微弱电压的形式存在[13], 如图 1所示.
|
图 1 核磁共振探测原理 Fig. 1 Magnetic Resonance Sounding (MRS) principle |
核磁共振信号如图 2所示, 是一个随e指数衰减的交流信号, 与地下水的含量及分布状态有关, 其表达式为:
|
图 2 核磁共振信号 Fig. 2 Magnetic Resonance Sounding (MRS) signal |
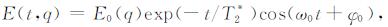
|
(1) |
式中, E0[nV]为信号的初始振幅, T2* [ms]为信号的自旋-自旋弛豫时间, q[A·ms]为激发脉冲矩(激发脉冲矩为激发电流与激发时间的乘积, 通常激发时间为40 ms), t[ms]为信号时间, ω0[rad/s]为信号角频率, φ0[°]为信号的初始相位[15].其中, E0反映了地下含水构造中含水量的大小, 是核磁共振信号的初始最大值, 其表达形式如式(2)所示[16]:
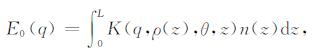
|
(2) |
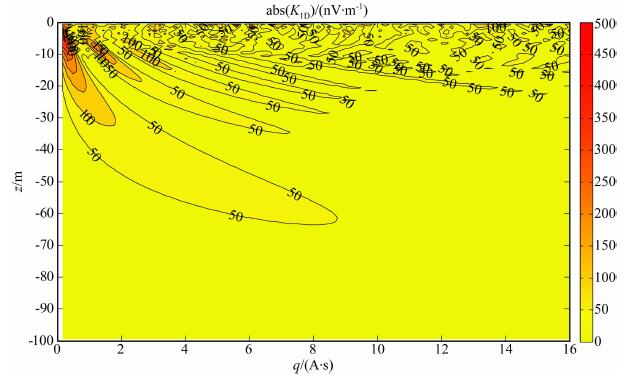
式中K[nV/m]为核函数, 反映了不同深度的地下水对核磁共振信号的作用, 与激发脉冲矩q[A·ms]、大地电阻率ρ(z)[Ωm]、含水层深度z[m]、地磁倾角θ[°]有关[17-20].假设地磁倾角为30°, 发射天线为双匝边长50m的方形线圈, 地层电阻率为500Ωm, 含水层厚度为1m并处于不同位置时, K的计算结果如图 3所示.图中, 横坐标代表激发脉冲矩q的大小, 纵轴代表含水层所在的深度, 色标代表所能够获得的核函数K的幅值.
|
图 3 双匝50 m方形线圈的核函数计算结果 Fig. 3 Kernel function computational results of single double turns 50 meters square coil |
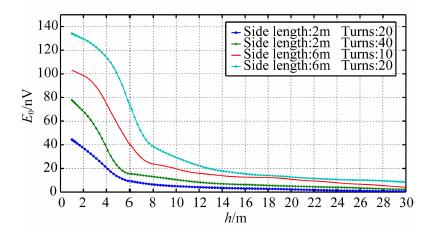
根据K值计算结果, 可以得到不同边长、匝数的线圈对不同深度的含水层进行探测时初始信号振幅E0的大小.假设含水层的厚度为1 m, 含水量为100%, E0随深度变化关系如图 4所示.可以看出, 线圈边长越大、匝数越高, 即接收信号的有效面积越大, 所获得的信号也越强, 而随着深度h的增加, E0会逐渐减小.核磁共振方法的探测深度与E0和仪器检测的最小分辨率有关, 假设仪器检测系统能够检测的最小信号幅度为10nV, 探测深度即为含水层产生E0为10nV时所在的深度.
|
图 4 线圈不同边长、匝数的E0-h曲线 Fig. 4 E0-h curves of different coil side length and the turns |
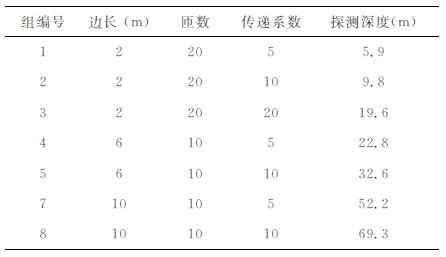
E0为接收线圈中所感应到信号的最大幅度, 可以认为是理想状态下能够获得的信号大小.但是实际测量过程中, 感应信号经过由线圈及匹配电路组成的谐振系统后, 其幅度和波形质量会由于系统传递特性作用而发生很大的变化, 影响探测效果.当谐振系统传递系数较高时, 可以提高检测系统接收到的E0幅度, 从而提高探测深度.假设含水层的厚度为1m, 含水量为100%, 不同传递特性对线圈探测深度影响关系如表 1所示.
|
|
表 1 传递系数对探测深度的影响 Table 1 The impact of transfer coefficient on detection depth |
从表 1中可以看出, 对于相同边长和匝数的线圈, 传递系数对探测深度的影响是明显的, 传递系数增大后, 可以显著提高探测深度, 同时改变所获得信号的波形质量.因此, 确定线圈的传递特性并分析其影响因素, 对提高小型多匝线圈的探测能力具有重要作用.
3 接收天线的传递特性对于核磁共振找水系统的接收线圈来说, 传递特性主要体现在品质因数和幅频特性两个方面.品质因数决定了线圈的选频能力, 高品质因数的线圈能够尽可能地压低噪声而获得信号[8].幅频特性决定了线圈的放大能力, 幅频特性理想的线圈能够有效放大信号, 使输出信号达到检测装置所要求的幅度水平[21].因此, 评价线圈对信号的响应时, 需要对这两种参数进行计算, 为分析线圈参数变化所产生的影响提供依据.
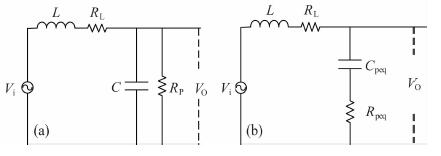
图 5a中给出了接收天线和匹配电路的实际电气模型, 其中, L为接收天线电感, RL为线圈内阻, C为配谐电容, RP为匹配电阻, Vi为线圈感应信号电动势的等效电压, VO为输出电压.由于实际电路属于混联形式, 为方便计算, 根据电路等效变换原理, 可以将图 5a所示的电路变换成如图 5b所示的标准RLC串联谐振电路. Cpeq为等效电容, Rpeq为等效电阻.
|
图 5 接收线圈计算模型 (a)接收线圈的电气模型; (b)等效电路模型. Fig. 5 Calculation model of receive coil (a) Receive coil electrical model; (b) Equivalent circuit model. |
根据等效变换原则, 变换前后的端口阻抗不变, 可以据此列出谐振回路端口的阻抗方程:
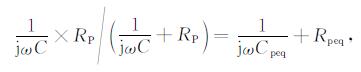
|
(3) |
方程中, C[F]为配谐电容, RP[Ω]为匹配电阻, Cpeq [F]为等效电容, Rpeq[Ω]为等效电阻, 整理得到:
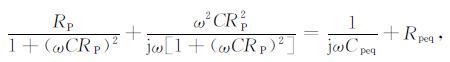
|
(4) |
根据方程两边参数不变原则, 有:
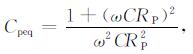
|
(5) |

|
(6) |
变换后的电路为标准的谐振电路形式, 其品质因数Q, 可以利用参数定义式进行计算[22]:
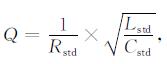
|
(7) |
其中

|
式中, Lstd[H]为标准谐振回路电感模型, Cstd[F]为标准谐振回路电容模型, Rstd[Ω]为标准谐振回路电阻模型, L[H]为接收天线电感, RL[Ω]为线圈内阻.将各标准模型的表达式代入式(7), 整理得到的品质因数计算式如下所示:
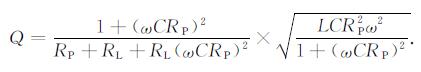
|
(8) |
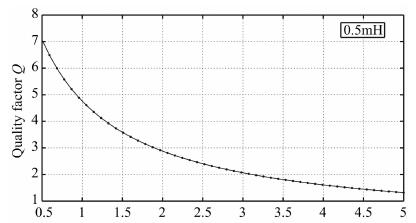
结合公式(8), 可以计算出不同线圈的品质因数随线圈内阻的变化关系. 图 6给出了电感系数为0. 5mH的线圈品质因数随内阻变化关系.
|
图 6 系统品质因数随线圈内阻的变化 Fig. 6 The change of system quality factor |
图 5b中的等效电路的电压转移函数可以写为:
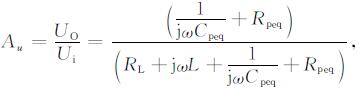
|
(9) |
式中Au为信号接收系统的电压转移函数.通常, 用电压转移函数的模|Au|随频率的变化表示系统的幅频特性H(ω), 对于本系统有:
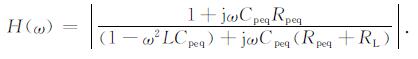
|
(10) |
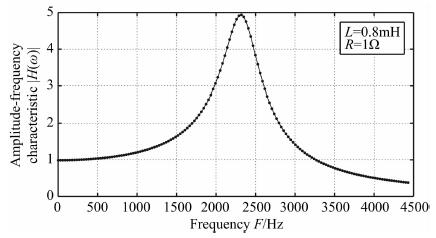
根据式(5)和式(6)给出的Cpeq和Rpeq值, 可以计算不同特征条件下线圈的幅频特性曲线, 如图 7所示.
|
图 7 幅频特性计算曲线 Fig. 7 Amplitude frequency characteristics calculation curve |
为表示系统的电压转移能力, 定义幅频特性的最大值H(ω)|max为系统的传递系数, 用符号α表示, 有
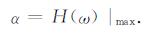
|
(11) |
结合式(10)和式(11), 利用MATLAB对幅频特性极值进行求解, 可以得到传递系数随线圈参数的变化关系.
4 传递特性影响因素分析对于接收线圈来说, 主要参数表现为线圈内阻和电感系数.本节通过理论计算, 讨论线圈参数对线圈幅频特性和品质因数的影响.同时, 根据现有的信号检测系统的分辨能力, 推导出接收线圈传递性能的临界值.
4.1 线圈参数的计算(1) 电阻的计算
线圈内部电缆的线径和环绕长度决定了线圈内阻的大小.由于线圈尺寸、线径的粗细各不相同, 其内阻差别也较大.根据电阻的常规计算公式, 有:
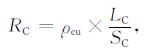
|
(12) |
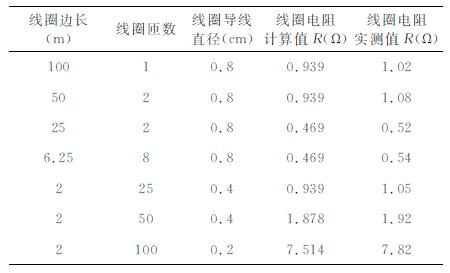
其中, RC[Ω]为线圈电阻, LC[m]为线圈环绕的长度, SC[m2]为线圈电缆的横截面积, ρcu[Ωm]为线圈的电阻率, 由线圈材质决定.不同结构线圈电阻值如表 2所示.
|
|
表 2 线圈电阻计算值 Table 2 The calculated value of coil resistance |
(2) 多匝线圈的电感计算
多匝线圈总电感是线圈自感与互感的累加.线圈自感lz[H]可根据公式直接求得[6]:

|
(13) |
其中μ0[H/m]为空间磁导率, D[m]为线圈内边长, n为线圈匝数, ε[m]为线圈匝间距, r[m]为线圈横截面半径.
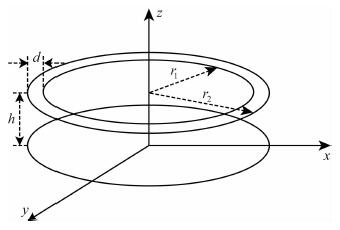
线圈的互感计算较为复杂, 需要考虑每一匝线圈对其邻近和周边(同一回路)的线圈影响, 同时需要考虑同层线圈匝间距离、层与层之间的距离对互感的影响.李军峰等人利用Kirchhoff公式, 给出了较为精确的螺线管型线圈的互感计算方法[23].多匝线圈互感计算模型如图 8所示.这里为方便, 利用圆形线圈进行计算, 圆形线圈与方形线圈的计算值有所不同, 但是差别为线性, 通过系数进行修正即可.
|
图 8 多匝线圈互感计算示意图 Fig. 8 Diagram of coils turns mutual inductance calculation |
任意两匝线圈的互感系数计算公式为:
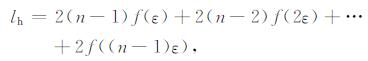
|
(14) |
其中:

|
式中, lh[H]为线圈互感, f(z)[H]为任意两匝线圈不同距离时的互感系数, z为存在互感的两个线圈间距离, d[m]为空心线圈最里层与最外层之间的宽度, ε[m]为线圈匝间距, h[m]为相邻两层线圈之间的高度, r[m]为各线圈的半径.通过每组之间的互感系数叠加的方式, 可求出整个装置的互感系数.线圈整体的电感系数为写作L[H], 计算式如(15)所示:

|
(15) |
利用这种方法得到的电感计算值精度较高. 表 3中给出了线圈电感的计算值与实测值.
|
|
表 3 线圈电感计算与实测值 Table 3 The calculated value of coil inductance |
由于测量环境的不同, 线圈的环绕边长从几米到几十米甚至上百米不等, 环绕的结构也分为单匝、多匝等不同的缠绕方式.如在地面上进行大规模地下水探测时, 一般采用边长为100m或者150m的单匝线圈, 而在矿井、隧道内的测量线圈, 由于受空间的限制, 需要采用边长为2m或者6m的多匝线圈测量[14].根据第3节的计算结果, 可以看出不同线圈的内阻、电感变化很大, 所产生的传递特性也存在着较大的差异.
(1) 线圈参数对品质因数的影响
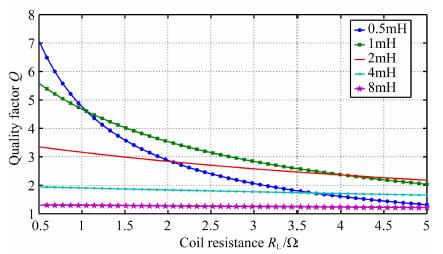
系统品质因数Q与线圈的电阻RL及电感量L相关.结合不同线圈的电感值, 给出线圈电阻对品质因数Q的影响, 如图 9所示.计算时, 假定信号频率为2326Hz, 负载电阻为100Ω.
|
图 9 传递系数随线圈电阻变化关系 Fig. 9 The change of transfer coefficient |
可以看出, 线圈的电感相同时, 随着内阻的增大, Q值均逐渐降低.在设计线圈时, 可通过降低线圈内阻获得更高的Q值.同时, 线圈电感和内阻本身对Q值的影响也需要同时考虑.当线圈的电感值偏离设计所需要的最佳值时, 电阻的影响会相对下降, 设计时需要综合平衡这两方面的因素.
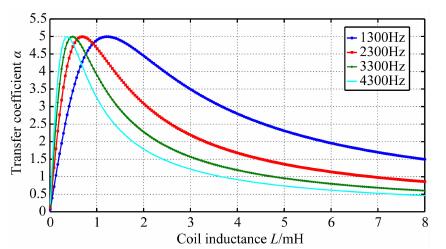
(2) 线圈电感对传递系数的影响
当线圈内阻和负载电阻固定时, 建立传递系数、谐振频率与线圈电感的对应关系, 如图 10所示.假设计算条件为:线圈内阻1Ω, 负载电阻100Ω.可以看出, 随着线圈内阻的变化, 传递系数存在一个极大值, 极大值所存在的位置即为最佳电感值.同时, 随着信号频率的改变, 最佳的电感值也会相应地发生变化.
|
图 10 传递系数随线圈电感变化关系 Fig. 10 The change of transfer coefficient with coil inductance |
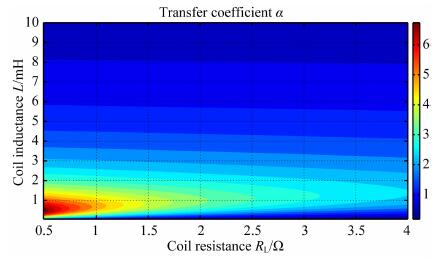
由以上两个关系可以得出, 在设计线圈时, 首先应根据所测量的信号频率、负载电阻等参数确定一个最佳的线圈电感值.其中, 核磁共振信号的频率与被测地区的地磁场有关, 全球范围内, 信号频率为1300Hz至3700Hz之间的某一个确定值.线圈电感值确定后, 需要尽可能地控制线圈内阻, 防止内阻过高而失去对信号的选频放大能力.基于此原理设计的线圈, 能够获得质量较好的核磁共振信号, 达到最佳的信号提取能力.以长春地区为例, 核磁共振信号频率为2326 Hz, 负载电阻为100Ω, 接收线圈参数不同时, 传递系数变化如图 11所示.线圈最佳参数应选择区域为色标偏红处, 此处所对应的线圈电感与电阻值所获得的传递系数最高, 对微弱信号的放大能力最强, 同时较低的电阻与合适的电感值使系统品质因数Q达到理想状态, 容易获得质量较好的信号波形.实际绕制线圈时可以此区域对应的参数为依据进行设计和制作.
|
图 11 最佳线圈的参数选择 Fig. 11 The best choice of coil parameters |
本文所研究的天线将与现有的核磁共振测量系统进行配合, 完成地下水的探测.在测量系统中, 信号采集单元由前置放大器、滤波器、末级放大器、模数转换板卡构成.信号采集单元的带宽为56~105Hz, 增益为103~107倍, 信号分辨率为10nV[1].当接收线圈的信号输出幅度小于系统的分辨率时, 将不能完成探测.
根据正演计算结果, 天线的感应信号幅度为E0[nV], 本文定义系统最小信号检测幅度为ξ[nV], 当天线的输出信号幅度等于检测系统的最小信号检测幅度时, 为临界状态, 此时天线的临界传递系数为αc, 有
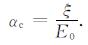
|
(16) |
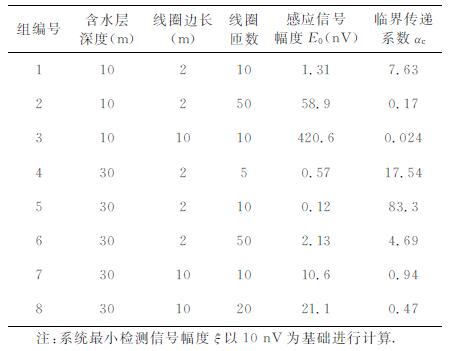
当传递系数α大于αc时, 天线的输出信号幅度高于最小信号检测幅度ξ, 测量系统能够探测到核磁共振信号, 反之, 当传递系数α小于αc时则无法对信号进行有效测量.利用公式(2)可以获得不同边长和匝数的线圈对不同深度的含水层进行探测时, 所获得的信号初始振幅E0, 假定检测系统能够检测的最小信号幅度为10nV, 可以计算出不同测量情况下的接收线圈传递系数临界值αc.如表 4所示.
|
|
表 4 不同参数天线计算的传递系数临界值 Table 4 Transfer coefficient critical value of different antenna parameter calculatio |
通过1、5组和2、6组计算可以看出, 对于相同匝数和边长的接收线圈, 探测深度越大临界系数越高; 通过4、5、6组计算和7、8组计算可以看出, 线圈匝数越高临界系数越低; 通过5、7组计算可以看出, 边长越大临界系数越低.临界系数反映了线圈理论上需要达到的传递系数与接收线圈实际传递系数之间的关系, 根据传递系数临界值的定义, 线圈的传递系数α需高于临界系数αc时才能获得有效信号, 下面将通过实际测试试验验证此推论.
5 实际测试测试试验利用吉林大学自主研制的核磁共振找水仪作为检测系统, 以不同天线的实际测量效果为基础, 验证上述结论.试验场地选择在长春市郊区西北一处已知地下水赋存情况的场地内进行, 利用JLMRS-I型核磁共振找水仪结合不同参数的探测天线进行实际探测.测量过程中, 将JLMRS-I型仪器设置为多匝线圈工作模式, 同时采集系统的中心频率、接收信号时间、系统死区时间、信号放大模块的增益均固定, 以保证每组试验的外部试验条件相同. 表 5中给出了验证接收信号波形试验的对比条件. 图 12中给出了不同参数的天线对地下20 m深处含水层的实际探测波形.根据钻井资料可知, 此含水层厚度为6. 5m, 含水量为15%, 含水层主要由粗砾石构成.
|
|
表 5 验证接收信号试验的对比条件 Table 5 Contrast conditions of verify the received signal test |
|
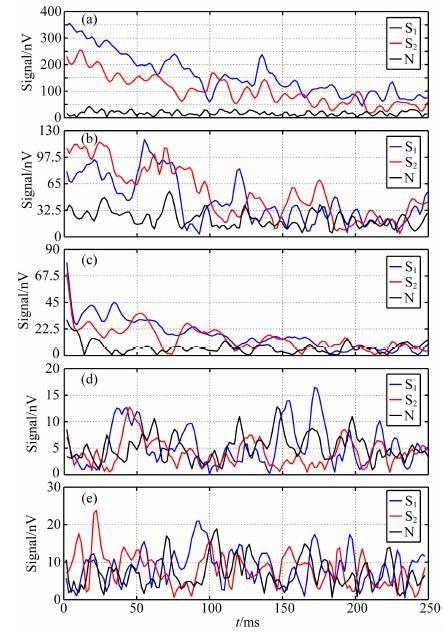
图 12 接收信号实测波形 (a) A组实验:实测α=4. 27, 计算αc=0. 056; (b) B组实验:实测α=3. 29, 计算αc=0. 12; (c) C组实验:实测α=4. 91, 计算αc=0. 13; (d) D组实验:实测α=1. 15, 计算αc=2. 55; (e) E组实验:实测α=0. 43, 计算αc=7. 81. Fig. 12 Receiving signals measured waves (a) Test A: measured α=4. 27, calculation αc=0. 056; (b) Test B: measured α=3. 29, calculation αc=0. 12; (c) Test C: measured α=4. 91, calculation αc=0. 13; (d) Test D: measured α=1. 15, calculation αc=2. 55; (e) Test E: measured α=0. 43, calculation αc=7. 81. |
表 5中给出的接收线圈内阻、电感系数为实测值, 初始振幅、传递系数、临界传递系数为理论计算值. 图 12中给出的波形为利用JLMRS-I型核磁共振找水仪对试验场地内地下水探测的现场实际波形, 蓝色线S1和红色线S2为两次激发获得的核磁共振信号, 黑色线N为测区空间电磁噪声.需要说明的是, 由于受到野外电磁噪声干扰, 测得信号的波形并不光滑, 信号存在波动.根据表 5对比条件和图 12试验结果, 可以看出:
(1) 当线圈传递系数高于其临界值时, 能够获得有效信号, 信号的幅度取决于线圈的等效面积和传递系数, 同时, 探测系统对噪声压制的能力受线圈Q值影响.如图 12(a-c)所示.试验A采用线圈的传递系数高于临界值70余倍, 获得的信号幅度达到360nV, 其Q值为4. 21, 探测数据中显示噪声完全被压制在底部, 信噪比理想.试验B的传递系数高于临界值20倍, 信号幅度为120nV小于试验A, 同时由于其Q值也低于试验A, 信号形态较差.试验C的传递系数仅高于临界值4倍, 信号与噪声分离并不明显, 信号幅度明显减小, 但是由于Q值的影响, 试验C所采用的线圈压制噪声能力优于试验A和试验B所采用的线圈.
(2) 当线圈传递系数低于其临界值时, 无法获得有效的核磁共振信号.如图 12(d-e)所示.试验D采用的线圈传递系数为1. 15, 低于其临界传递系数, 获得的信号基本淹没在噪声中, 信号数据不具有可信性, 无法对信号和噪声进行有效的分离.试验E采用更为极端的小型线圈, 其传递系数已经低于1, 对初始信号产生了衰减作用, 同样无法获得有效的核磁共振信号.结合本文对传递特性的计算和影响因素分析, 造成线圈无法获得信号的主要原因可以归结为:受线圈自身电阻和电感系数过大的影响, 传递系数过低, 在极端情况下甚至出现衰减状态, 对信号的放大输出后低于系统的最小检测幅度, 无法对信号进行有效检测.
6 结论根据本文计算结果和实际测试的信号波形, 可以得到如下结论:
(1) 接收线圈的传递系数决定了探测系统能否对地下水进行有效探测.当线圈的传递系数低于临界值时, 系统将无法得到有效的核磁共振信号.
(2) 接收天线的内阻与电感系数对传递特性具有重要影响.计算和实测结果表明, 天线内阻值较低、电感值越趋近于最佳, 传递特性越好, 在中心频点的增益越高, 选频特性越好.反之, 当天线的内阻与电感值过高时, 将无法对核磁共振信号进行有效响应.
(3) 通过提高信号采集系统的微弱信号检测能力, 可以弥补天线传递特性自身的不足.当仪器系统能够对更小的信号进行检测时, 传递系数的临界值也会随之降低, 传递特性较差的线圈也会满足测量要求.
随着核磁共振地下水测量的应用环境越来越复杂, 探测天线的结构、尺寸将会发生很大的变化.进行复杂环境的核磁共振探测天线设计时, 可以利用本文得出的结论作为参考, 首先保证天线的传递系数高于临界值, 使系统能够有效探测地下水信号, 然后进一步将线圈的电阻与电感值调整至最佳, 以提高接收信号质量, 保证核磁共振方法对地下水的探测效果.在此基础上, 我们将继续研究多匝环形线圈绕制方法与工艺、噪声压制方法和数据处理手段, 提高测量信噪比, 以解决利用核磁共振方法在复杂地形环境下找水及在隧道、矿井等限定空间下对灾害水源进行探测的难题.
| [1] | 林君, 段清明, 王应吉, 等. 核磁共振找水仪原理与应用. 北京: 科学出版社, 2010 : 2 -3. Lin J, Duan Q M, Wang Y J, et al. Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications (in Chinese). Beijing: Science Press, 2010 : 2 -3. |
| [2] | 翁爱华, 王雪秋, 刘国兴, 等. 导电性影响的地面核磁共振反演. 地球物理学报 , 2007, 50(3): 890–896. Weng A H, Wang X Q, Liu G X, et al. Nonlinear inversion of surface nuclear magnetic resonance over electrically conductive medium. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 890-896. |
| [3] | Legchenko A, Baltassata J M, Beaucea A, et al. Nuclear magnetic resonance as a geophysical tool for hydrogeologists. Journal of Applied Geophysics , 2002, 50(1-2): 21-46. DOI:10.1016/S0926-9851(02)00128-3 |
| [4] | 蒋川东, 林君, 段清明, 等. 二维阵列线圈核磁共振地下水探测理论研究. 地球物理学报 , 2011, 54(11): 2973–2983. Jiang C D, Lin J, Duan Q M, et al. A study on 2D Magnetic Resonance Sounding with an array loop for groundwater exploration. Chinese J. Geophys. (in Chinese) , 2011, 54(11): 2973-2983. |
| [5] | 林君. 核磁共振找水技术的研究现状与发展趋势. 地球物理学进展 , 2010, 25(2): 681–691. Lin J. Situation and progress of nuclear magnetic resonance technique for groundwater investigations. Progress in Geophysics (in Chinese) , 2010, 25(2): 681-691. |
| [6] | Lubczynski M, Roy J. Hydrogeological interpretation and potential of the new magnetic resonance sounding (MRS) method. Journal of Hydrology , 2003, 283(1-4): 19-40. DOI:10.1016/S0022-1694(03)00170-7 |
| [7] | Roy J, Lubczynski M. The magnetic resonance sounding technique and its use for groundwater investigations. Hydrogeology Journal , 2003, 11(4): 455-465. DOI:10.1007/s10040-003-0254-8 |
| [8] | Legchenko A, Valla P. A review of the basic principles for proton magnetic resonance sounding measurements. Journal of Applied Geophysics , 2002, 50(1-2): 3-19. DOI:10.1016/S0926-9851(02)00127-1 |
| [9] | Walsh D O. Multi-channel surface NMR instrumentation and software for 1D/2D groundwater investigations. Journal of Applied Geophysics , 2008, 66(3-4): 140-150. DOI:10.1016/j.jappgeo.2008.03.006 |
| [10] | 荣亮亮.核磁共振多匝线圈找水技术研究.长春:吉林大学, 2009: 44. Rong L L. Study on multi-turn loop Magnetic Resonance Sounding (MRS) technique for underground water (in Chinese). Changchun: Jilin University, 2009: 44. |
| [11] | Greben J M, Meyer R, Kimmie Z. The underground application of Magnetic Resonance Soundings. Journal of Applied Geophysics , 2011, 75(2): 220-226. DOI:10.1016/j.jappgeo.2011.06.010 |
| [12] | 潘玉玲, 张昌达. 地面核磁共振找水理论和方法. 武汉: 中国地质大学出版社, 2000 : 37 . Pan Y L, Zhang C D. The Theory and Method of SNMR (in Chinese). Wuhan: China University of Geosciences Press, 2000 : 37 . |
| [13] | 王应吉, 林君, 荣亮亮, 等. 地面核磁共振找水仪放大器设计. 仪器仪表学报 , 2008, 29(8): 1627–1632. Wang Y J, Lin J, Rong L L, et al. Amplifier design of surface nuclear magnetic resonance instrument for underground water investigation. Chinese Journal of Scientific Instrument (in Chinese) , 2008, 29(8): 1627-1632. |
| [14] | 于景邨. 矿井瞬变电磁法勘探. 徐州: 中国矿业大学出版社, 2007 : 5 -8. Yu J C. The Detection of Mine Transient Electromagnetic Method (in Chinese). Xuzhou: China University of Mining and Technology Press, 2007 : 5 -8. |
| [15] | 李振宇, 李俊丽, 潘玉玲. 地面核磁共振找水方法综述. 勘探地球物理进展 , 2002, 25(6): 55–58. Li Z Y, Li J L, Pan Y L. Summary of groundwater detection with surface nuclear magnetic resonance method. Progress in Exploration Geophysics (in Chinese) , 2002, 25(6): 55-58. |
| [16] | 翁爱华, 李舟波, 王雪秋. 层状导电介质中地面核磁共振响应特征理论研究. 地球物理学报 , 2004, 47(1): 156–163. Weng A H, Li Z B, Wang X Q. A study on surface nuclear magnetic resonance over layered conductive earth. Chinese J. Geophys. (in Chinese) , 2004, 47(1): 156-163. |
| [17] | Braun M, Hertrich M, Yaramanci U. Study on complex inversion of magnetic resonance sounding signals. Near Surface Geophysics , 2005, 3(3): 155-163. |
| [18] | Mueller-Petke M, Yaramanci U. QT inversion-Comprehensive use of the complete surface NMR data set. Geophysics , 2009, 75(4): WA199. |
| [19] | Girard J F, Boucher M, Legchenko A, et al. 2D magnetic resonance tomography applied to karstic conduit imaging. Journal of Applied Geophysics , 2007, 63(3-4): 103-116. DOI:10.1016/j.jappgeo.2007.08.001 |
| [20] | Legchenko A, Ezersky M, Girard J F, et al. Interpretation of magnetic resonance soundings in rocks with high electrical conductivity. Journal of Applied Geophysics , 2008, 66(3-4): 118-127. DOI:10.1016/j.jappgeo.2008.04.002 |
| [21] | Strehl S. Development of Strategies for Improved Filtering and Fitting of SNMR-Signals. Technical University of Berlin, Institute of Applied Geosciences, Department of Applied Geophysics Diplomarbeit, 2006. |
| [22] | 陈希有. 电路理论基础. 北京: 高等教育出版社, 2010 . Chen X Y. Fundamentals of Circuit Theory (in Chinese). Beijing: Higher Education Press, 2010 . |
| [23] | 李军峰, 李文杰. 航空电磁发射线圈自感系数的精确计算. 物探化探计算技术 , 2007, 29(S1): 17–20. Li J F, Li W J. A calculation method of self-inductance of transmitting coil for AEM system. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2007, 29(S1): 17-20. |
 2013, Vol. 56
2013, Vol. 56