2. 中石油东方地球物理公司, 河北涿州 072750;
3. 中国地质调查局发展研究中心, 北京 100037
2. Bureau of Geophysical Prospecting, China National Petroleum Corp., Hebei Zhuozhou 072750, China;
3. Development and Research Centre of China Geological Survey, Beijing 100037, China
这里以HansonR. O.和MiyazakiY.的论文[1] (1984)为基础定义"曲化平用最佳等效源模型". "曲化平用最佳等效源模型"是指位于观测曲面近下方、平行于测点切平面、中心投影与测点重合、平面投影为矩形、偶极矢量沿测点切平面外法线方向的空间平行四边形偶层面.该最佳等效源模型定义中的近下方指≤2个点距; 矩形指由测线距Δx和测点距Δy形成的矩形.
"曲化平"是指观测曲面上的实测位场向位于观测曲面最高点或其上方水平面的解析延拓计算.有的"曲化平"要求化平面穿越观测面, 或位于观测面最低处, 或其下方, 这实际上包含了复杂而不稳定的向下延拓计算.在地面为观测曲面时, 不同规模的异常源可能位于观测面最高点和最低点平面之间.因为下延不能过场源, 则下延前, 应先分开不同深度场源的异常场, 再分别下延, 这使问题更加复杂化.故本文不考虑上述复杂情况.
我们称上述等效源模型为最佳, 一是认真比较了国内外文献中发表的大量曲面延拓和曲化平方法的优、缺点之后而得出; 二是采用该"最佳等效源模型"研制位场曲化平实用程序之后而确认.
本文参考文献, 给出了10类位场"曲面延拓和曲化平方法": ① 逆演(sinx/x)·(siny/y)方法(其实质是在空间域实现的波数域方法)[2-3]; ② 球谐分析方法(其主要用于局部异常下延, 不适合综合异常的上下延拓)[4-7]; ③ 等效源方法(主要是"偶层位法")[1, 8-26]; ④ 调和级数法(其原理有问题)[27]; ⑤ 正弦级数法(较调和级数法好, 但也有争议)[28-29]; ⑥ 解拉普拉斯方程第一边值问题的差分法(它是一种不便实施的"矩形网格迭代法")[3]; ⑦ 泰勒级数法(也称镜像法, 它采用了以FFT计算曲面上异常各阶垂向导数的"近似且不稳定的迭代算法")[8, 30]; ⑧ 格林公式法(这是并没有按公式要求实现的算法)[20, 31]; ⑨ 波数域迭代法(主要用于下延, 且迭代不总是收敛)[7, 32-35]; ⑩ 解拉普拉斯方程第一边值问题的三角函数法(其理论严密、精度高, 但要求采用不等间距采样等诸多技术措施, 难被一般技术人员掌握)[22-24, 36].
由上面方法③有20个参考文献可见, "偶层位等效源"方法最受重视.其中, 潘作枢等方法精度较高, 但在"偶极方向l0 "选择和设计偶层网格方面技术性较强, 难被一般技术人员掌握.侯重初与蔡宗熹、管志宁与安玉林等, 因为致力于建立"曲线上和曲面上位场转换系统", 没能在"位场上延"方法探索上下更大功夫.文献[26]采用"严密拼接在一起的组合空间三角形偶层面逼近观测面"的"三角形偶层位模型", 但是"单个三角形偶层面位场"表达式过于复杂, 计算速度很慢, 求解偶极强度又很不稳定, 上延精度差.
安玉林对第②[6]、③ [18]、⑥(见原地质部航空物探大队1979年编《航磁见矿100例》)、⑨ [7]等4类方法均曾做过认真研究; 还验证过文献[26]方法的有效性.为了研制出能够同时实现高精度、高速度、大数据量和便于接图的曲化平程序, 经过严格比较, 最终选定文献[1]提出的"空间平行四边形偶层位等效源模型".
该偶层等效源模型之所以最佳, 主要是因为它具有如下综合优势:
第一, 各测点下放一模型.按照偶层位理论[8], 该"等效源模型"组合对于观测曲面的接近程度优于众多其它形式的离散型等效源模型组合.在观测面起伏不是特别大的情况下, 该"等效源模型"组合可与观测曲面近距离地同步起伏, 因而等效效果不仅优异, 而且全区一致.
第二, 除偶极子等少数模型外, 该"等效源模型"的单位位场表达式Iij(x, y, z)(即偶极强度μij=1的位场表达式)最简短(见第2节(12)式), 且没有需要特殊处理的奇异计算点, 因而在建立求解偶极强度μij的联立方程组时, 生成系数Iij(x, y, z)矩阵的计算量很小, 大大提高了计算速度.
第三, 系数Iij(x, y, z)矩阵的主对角线元素具有绝对优势或明显优势(详见第2节), 因而可以采用高斯-赛德尔迭代法, 求解所建立的巨大维数方程组, 算法稳定, 收敛速度很快.
第四, 在上述三方面优势的基础上, 还可以进一步采取如下技术方案: ① 61×61或更大的对称窗口逐点滑动方案; ② 方程组系数矩阵的非零Iij(x, y, z)元素以二进制存储于硬盘中的压缩存储方案; ③ μij初次反演值与由迭代反演得到的多次剩余反演值累加方案.采用这些技术方案, 提高了计算精度, 保证了算区边部严格接图.
采用该"最佳等效源模型", 我们成功地研制出了能够同时实现高精度、高速度、大数据量和便于接图与使用的单线程曲化平程序.如果采用多核计算机, 该程序很容易实施并行计算.该程序已经纳入中国地质调查局发展研究中心开发的RGIS (重磁电数据处理解释软件)中.
2 最佳等效源模型的单位位场积分表达式假设[1]:直角坐标系的z坐标及其对应坐标ζ和γ向上为正; 观测曲面为E, 观测网格为矩形, 观测点为(α, β, γ), γ=γ(α, β), 线距、点距分别为Δx和Δy, 线数、点数分别为M和N, 观测位场记为U(α, β, γ); 延拓曲面为C, 其上点的坐标为(x, y, z), 位场函数记为U(x, y, z); 起伏偶层面为D, 其上点为(ξ, η, ζ), ζ=ζ(ξ, η); D上偶极强度模为μ(ξ, η), 偶极方向与测点切平面外法线重合, 单位矢量为n(ξ, η); 三个面由上至下为C、E、D.矢量r=(x-ξ, y-η, z-ζ)或r=(α-ξ, β-η, γ-ζ), r=|r|.在上述条件下, 该起伏偶层面的位场(重磁场均视为位场)可表示为
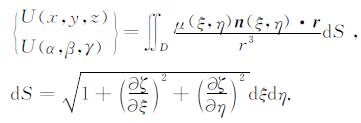
|
(1) |
可以把该偶层面近似表示成"曲化平用最佳等效源模型"组合.采用这种近似, (1)式中U(x, y, z)变为
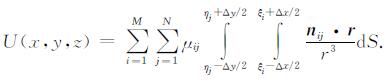
|
(2) |
而当μij=1时, 第ij个最佳等效源模型的单位位场积分表达式可写为
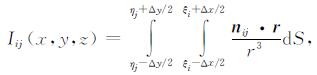
|
(3) |
此时, Iij(x, y, z)的积分表达式实际上是
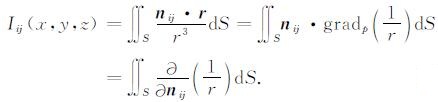
|
(4) |
据偶层位理论[8]可知, 该积分值是第ij最佳等效源模型对观测点所张立体角Ωij的负数, 即Iij(x, y, z)=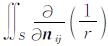
Iij(x, y, z)的积分表达式可以具体化.为了简单, 且不失一般性, 假定:第ij空间平行四边形偶层面中心置于坐标系原点(0, 0, 0), 该面上点的坐标仍以(ξ, η, ζ)表示.则(3)式的积分应改写为
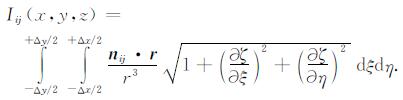
|
(5) |
因为
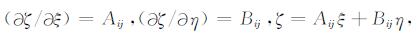
|
(6) |
则有
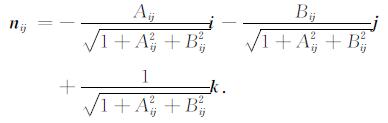
|
(8) |
把(6)-(8)式代入(5)式, 再为了简便而舍掉下角标, 得到
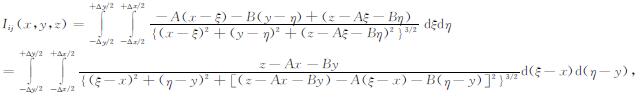
|
(9) |
再令:

|
(10) |
则
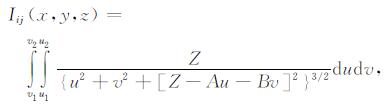
|
(11) |
Z、A、B与积分变量无关, 所以Iij(x, y, z)的被积函数在形式上相当简单.
由(11)式立即可见, 当计算点位于x≤Δx/2与y≤Δy/2范围之外的Z=z-Ax-By=0平面上时, 即当计算点位于最佳等效源模型向外的延展面上时, Iij(x, y, z)=0, 这与前面由偶层位理论得出的结论相同.
采用第3节中的变量置换法积分公式[37-38], 经过复杂的推导, 可以得到Iij(x, y, z)的极其复杂的表达式(见第4节(28)式).而采用模型变换法, 可以得到Iij(x, y, z)的另一个极为简短的表达式(见下面第5节(41)式), 即
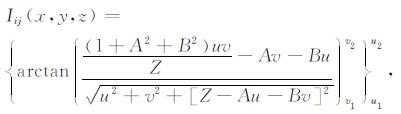
|
(12) |
将(12)式代入(2)式, 即得观测点位场表达式
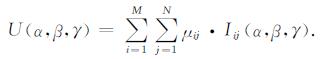
|
(13) |
实现位场曲化平的关键是由观测位场值U(α, β, γ)求解偶极强度μij.根据(13)式可以建立求解μij的联立方程组, 其系数矩阵元素由Iij(α, β, γ)形成.根据本节前面对Iij(α, β, γ)取值的分析可知:整个等效源组合面在第ij观测点产生的位场主要是第ij偶层面的贡献.其原因是: ① 坡度A、B的变化具有连续性, 第ij面周围紧邻的面在第ij个观测点产生的位场值, 近似为0; ② 远离第ij面的面在第ij观测点产生的位场值, 随距离增大而迅速变小.据此可知, 最佳等效源模型与观测曲面相当近的情况下, 方程组系数矩阵的主对角线元素具有绝对优势; 即使最佳等效源模型与观测曲面有一定距离(≤2个点距), 方程组系数矩阵的主对角线元素仍然具有较大优势.
求得所有组合单元的偶极强度μij后, 在选定的起伏面或平面上的计算点, 按(13)式(其中(α, β, γ)⇒(x, y, z))进行计算, 即可得到位场曲面延拓或曲化平结果.
3 几个变量置换法积分公式文献[1]没有给出(我们至今也没有见到)Iij(x, y, z)积分表达式(11)到Iij(x, y, z)解析表达式(12)的推导过程; 该文作者仅指出, 其推导过程是相当复杂的, 并列出了进行推导的参考文献.我们曾按其列出的参考文献的积分方案进行推导, 但由于积分过程非常复杂而没有得到积分结果, 于是改用变量置换法对(11)式进行积分(见第4节).为了第4节的论述方便, 本节列出推导中所采用的4个积分公式.我们对这些积分公式均进行了严格验证.因为除(14)式外, (15)-(21)式在一般数学手册中很难找到, 故在正文中列出, 以便于他人参考应用.
(1) 不定积分公式(参见文献[37]264页)
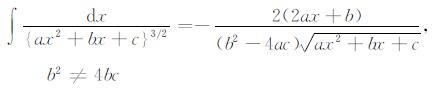
|
(14) |
(2) 定积分公式(参见文献[38]83页)
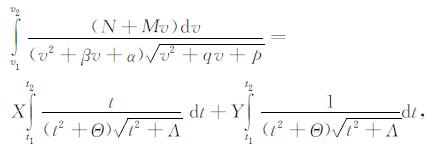
|
(15) |
其变量置换式为
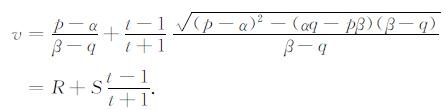
|
(16) |
在(16)和(15)式中,
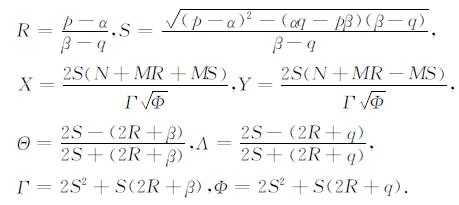
|
(17) |
(3) 定积分公式(参见文献[38]83页)
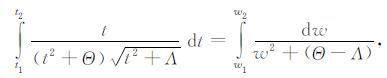
|
(18) |
其变量置换为
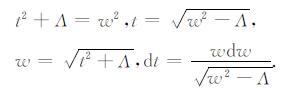
|
(19) |
(4) 定积分公式(参见文献[38]83页)
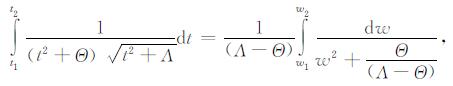
|
(20) |
其变量置换为
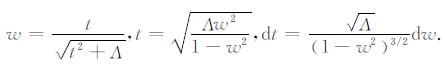
|
(21) |
空间平行四边形偶层面产生的单位位场可表示为如下积分(即(11)式):
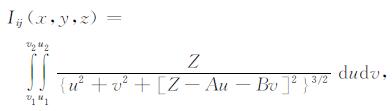
|
(22) |
对(22)式分母变形如下:
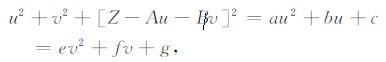
|
其中,
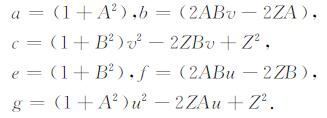
|
因为
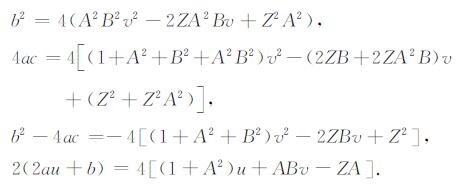
|
所以, 直接采用积分式(14), 得到
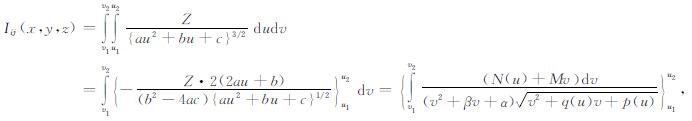
|
(23) |
其中,
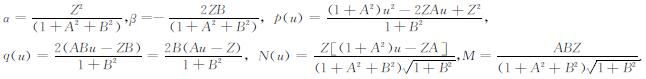
|
(24) |
由(15)-(17)式, 可得
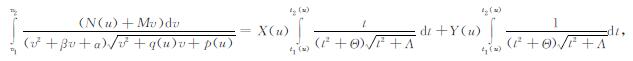
|
(25) |
其中,
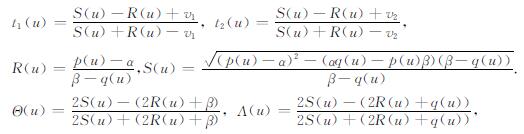
|
(26) |

|
(27) |
采用(18)和(19)式, 以及经编程计算证明的Θ > 0, (Θ-Λ) < 0, 可求得(25)式右端第一个积分的积分结果(为含有对数型函数的表达式); 而采用(20)和(21)式, 以及Θ/(Λ -Θ) > 0, 可求得(25)式右端第二个积分的积分结果(为含有反正切型函数的表达式); 再经编程计算证明
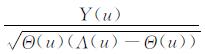
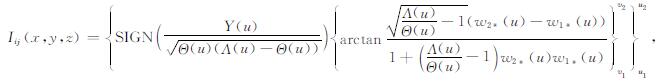
|
(28) |
其中, SIGN (…)为符号函数(取值±1), 而函数
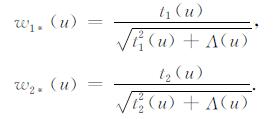
|
(29) |
显然, (28)式比(12)式复杂很多!
这里补充指出如下3点:
(1) 在上面给出的推导过程中, 两处出现"经编程计算证明"等文字.这是因为推导过程中涉及的有关函数(见(26)和(27)两式)太复杂, 难以采用严格理论推导的方法得出其取值规律, 故改用编程计算加以确定, 用以辅助上述推导过程, 最终导出了与前面位场理论相符的(28)式.
(2) 从数学角度看, (28)式的推导不尽严谨, 但编程试算证明该式与(12)式完全等价.
(3) 因涉及(29)、(26)和(27)式, (28)式变得非常复杂, 还要特殊处理奇异点数值计算问题, 致使程序计算速度很慢, 精度也较差, 故采用(28)式编制的曲化平程序软件, 不具有实用性, 最终被放弃.
5 推导最佳等效源模型单位位场表达式的模型变换法如前所述, 按两种积分方案, 均没能由Iij(x, y, z)积分表达式(11)推导出Iij(x, y, z)的解析表达式(12).这迫使我们必须另辟蹊径, 并且终于找到了一种求解其单位位场正演积分的模型变换法.其具体做法是: ① 采用变量置换法求得该模型在三种较简单情况下(即A=B=0; A≠0, B=0; A=0, B ≠0)的单位位场正演解析表达式, 并把它们写成相同结构形式, 找出其中的变换不变量和变换变化量. ② 确定变换变化量随模型变换的变化规律:即随着模型中坡度A, B的变化, 正演表达式中的变换变化量产生怎样的变化. ③ 通过对变换变化量中的参数代换, 最终导出最佳等效源模型的单位位场正演解析表达式.
5.1 坡度A=B=0水平矩形偶层面的Iij(x, y, z)表达式此时, 把偶层面的坡度A=B=0和Z=z, 代入公式(24), 得到
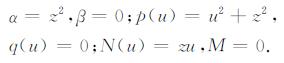
|
(30) |
再由公式(23), 有
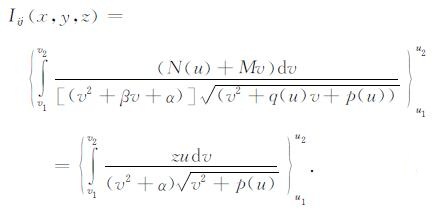
|
(31) |
采用(20)和(21)式, 完成(31)式积分, 得到
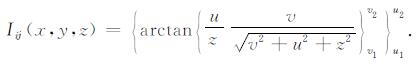
|
(32) |
(32)式可以改写为
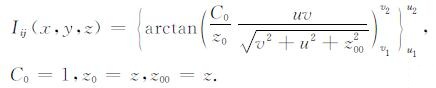
|
(33) |
此时A≠0、B=0和Z=z-Ax, 即偶层面沿ξ方向倾斜, 代入公式(24), 则有
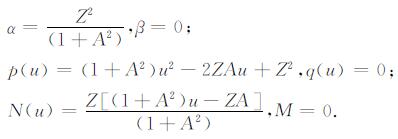
|
(34) |
再由公式(23), 有
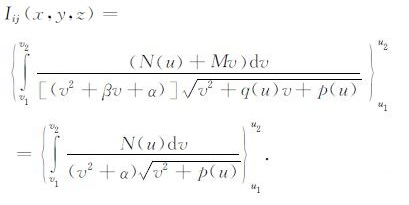
|
(35) |
采用(20)和(21)式, 完成(35)式积分, 得到
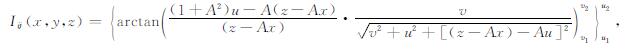
|
(36) |
(36)式可以改写为
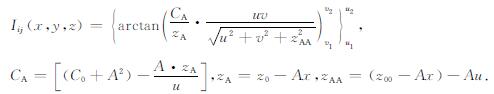
|
(37) |
此时A=0、B≠0和Z=z-By, 即偶层面沿η方向倾斜.根据与5.2节所提问题的对称关系, 由(36)式, 可以写出如下表达式:
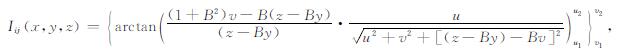
|
(38) |
(38)式可以改写为
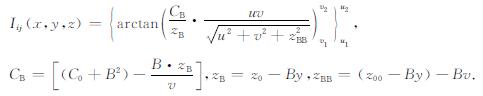
|
(39) |
表达式(33)、(37)和(39)具有相同的结构, 其中, C(), z(), z()()是变化量, u和v是非变化量.此三式为推导坡度A≠0、B≠0的空间平行四边形偶层面的Iij(x, y, z)表达式(即后面(41)式)奠定了基础.下面将采用由"最佳等效源模型空间" (简称模型空间)到其"单位位场表达式空间"(简称位场空间)连续而一一对应的映射理论, 给出该偶层面的Iij(x, y, z)表达式的推导过程.
为此, 把坡度A、B分别以ΔA(≠0)、ΔB(≠0)等分为K、L等份, 则A=K·ΔA、B=L·ΔB, 当ΔA→0、ΔB→0时, K、L很大.现在, 选坡度对(k· ΔA, l·ΔB), k=0, 1, …, K, l=0, 1, …, L, 则在[0~A, 0~B]区间内, 形成(K+1)×(L+1)个"坡度对矩形点阵"(简称矩形点阵).其中, 坡度对(0, 0)、(A, 0)、(0, B)位于矩形点阵的三个角点处, 分别对应模型空间的水平矩形模型、沿ξ方向坡度为A投影为Δx的矩形模型、沿η方向坡度为B投影为Δy的矩形模型、以及位场空间中结构形式一致的表达式(33)、(37)、(39).就是说, 通过坡度对建立起了模型空间中模型与位场空间中表达式之间的对应关系(即映射关系), 而且因为A和B彼此独立无关故映射是一对一的.
根据位场理论, 同类型的、具有彼此独立无关参数的"位场模型空间"中距离很小的两个模型, 其在"位场表达式空间"中对应的两个表达式的距离也是很小的.这表明"位场模型空间"二元素与"位场表达式空间"对应二元素之间的映射是连续的; 而这里的模型空间和位场空间之间的映射更是如此.
根据映射的"连续和一一对应"性质, 当(0, 0)号模型绕η轴以ΔA为步长转动K次到(A, 0)模型时, 相当于模型沿"矩形点阵"的(k·ΔA, 0)边变动; 当ΔA→0时, 其(1×ΔA, 0)模型和((K-1)· ΔA, 0)模型对应的单位位场表达式的极限分别是(33)式和(37)式.当(0, 0)号模型绕ξ轴以ΔB为步长转动L次到(0, B)模型时, 相当于模型沿"矩形点阵"的(0, l·ΔB)边变动; 当ΔB→0时, 其(0, 1× ΔB)模型和(0, (L-1)·ΔB)模型对应的单位位场表达式的极限分别是(33)式和(39)式.同理, 当(A, 0)号模型绕ξ轴以ΔB为步长旋转L次到(A, B)模型时, 相当于模型沿"矩形点阵"(A, l·ΔB)边变动; 当ΔB→0时, 其(A, 1×ΔB)模型和(A, (L-1)·ΔB)模型对应的单位位场表达式的极限分别是(37)式和(A, B)模型的单位位场表达式(即后面的(41)式).
进一步分析可知, 无论(0, 0)号模型, 还是(A, 0)号模型, 绕ξ轴以ΔB为步长转动, 转动前, 沿η轴方向的所有直线均是水平的, 转动第l次和转动L次终止(即分别转到(0, B)模型与(A, B)模型)时, 所有直线的倾斜角度与伸长长度均相同, 投影长度也均等于Δy, 而与ξ轴方向线的倾角是0还是A无关.也就是说, 上述两种转动引起的模型的变化方式和变化量都相同, 只是起点不同, 因而(0, B)模型与(A, B)模型的位场表达式中变化量的变化规律应该相同, 不同之处仅在于其初始量z(), z()(), C()不同.这就是说, (A, B)模型的单位位场表达式的形式也取(39)式, 只是其变化量的初始量要以zA, zAA, CA来代替.代替后得到(40)式, 用z′B、z′BB和C′B记该式中的变化量(实际就是(41)式对应的变化量), 则(40)式为
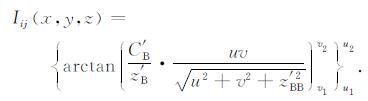
|
(40) |
(40)式实际上是第一次初值回代结果, 给出了Iij(x, y, z)解析表达式的基本结构.下面将继续采用初值回代法导出z′B、z′BB、C′B的具体形式:
① 用(37)式中的zA=z0 -Ax代替(39)式内zB=z0 -By中的z0, 得z′B=z0 -Ax-By; 再以(33)式中的起始初值z0=z代换z′B表达式中的z0, 即得z′B=z-Ax-By=Z.
② 用(37)式中的zAA=(z00 -Ax-Au)代替(39)式内zBB=(z00 -By)-Bv中的z00, 得z′BB=(z00 -Ax-Au)-By-Bv; 再以(33)式中的起始初值z00=z代换z′BB表达式中的z00, 即得z′BB=Z-Au-Bv.
③ 用(37)式中的CA=C0+A2-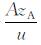
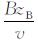
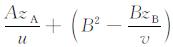
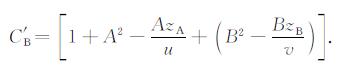
|
(40a) |
该式是C′B的第一层次初值回代, 给出了C′B的基本结构. C′B中的zA和zB形式上均只是模型一次旋转的显示, 为了显示出模型分别绕η轴和ξ轴两次旋转, 还需要继续进行初值代换, 以求出C′B的最终结果, 称之为第二层次初值回代.又因为各自绕轴旋转作用彼此独立, 旋转顺序可以互换, 故两次接续旋转作用的合成结果, 等于第一次旋转结果作为第二次旋转初值的旋转结果.这就是说, zB=z0-By中的z0应以zA代替, zA=z0-Ax中的z0应以zB代替.然后再以(33)式中的起始初值z0=z代换所得两个新式中的z0.其回代过程可表示如下:
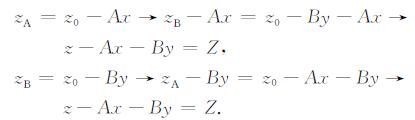
|
将上述结果代入(40a)式, 即得
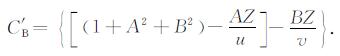
|
把z′B、z′BB和C′B代入(40)式, 最终得到
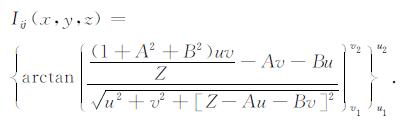
|
(41) |
其中

|
(42) |
(41)和(42)式合起来就是最佳等效源模型的单位位场表达式, 亦即文献[1]中的公式.
这种推导单位位场正演解析表达式的新方法可命名为"模型旋转变换法", 简称"模型变换法", 它是基于模型与其位场正演表达式之间连续的、一一对应的映射关系提出的.它不同于重力和磁力勘探专业经常采用的"变量置换积分法"、"坐标变换积分法"和"体积分变面积分、面积分变线积分积分法".这种新方法, 在条件满足时, 为寻找某些复杂积分的简短积分结果提供了一条可能的途径.
6 结论和建议(1) 在文献[1]的基础上, 本文定义了"曲化平用最佳等效源模型", 并严格推导出了该模型面(即空间平行四边形偶层面)的单位位场表达式.该表达式非常简短, 采用它研制的实用化"曲化平程序软件"能够同时实现高精度、高速度和大数据量曲化平计算.因此, 建议在以后的重磁专业教科书中, 编入这里推出的"最佳等效源模型"的单位位场表达式.
(2) 本文给出的推导空间平行四边形偶层位场正演公式的模型变换法, 具有一定的普遍性, 建议位场理论和方法研究者对此方法给予关注, 以便在自己的研究实践中遇到类似问题时, 参考、试用, 并予以发展、完善.
(3) 本文还给出一个重要启示:采用不同的思路和方法求解同一积分, 可能得到等价但复杂程度非常悬殊的结果.据此研制出的程序软件的效果就大不相同.因此, 建议方法技术研究人员研究以积分为基础的方法软件时, 要广开思路, 追求最佳积分结果, 从源头上保证和提升方法和软件的效果.
(4) 作者以往的方法技术研究实践同样证明(见文献[6]107-108页和文献[39]129-132页), 无论推导何种公式, 多采取几种推导方案, 定会得到复杂程度和应用效果非常悬殊的结果.因此, 建议方法技术研究人员推导公式的时候, 多考虑几种推导方案, 选取其中最佳结果.
| [1] | Hanson R O, Miyazaki Y. Continuation of potential fields between arbitrary surfaces. Geophysics , 1984, 49(6): 787-795. DOI:10.1190/1.1441707 |
| [2] |
Oldham C H G.
The |
| [3] | 张培琴. 将起伏地形上的位场值换算到同一水平面. 物探与化探 , 1979, 1(3): 10–32. Zhang P Q. Transforming potential field values on undulate terrain to horizontal plane. Geophysical and Geochemical Exploration (in Chinese) , 1979, 1(3): 10-32. |
| [4] | 王忠敏, 张喜丰. 在任意起伏地形曲面上观测的三维场解析延拓. 物化探研究报导 , 1980(5): 267–271. Wang Z M, Zhang X F. The analytical continuation for three-dimensional potential from an arbitrary surface. Bulletin of Institute of Geophysical and Geochemical Prospecting (in Chinese) , 1980(5): 267-271. |
| [5] | 梁锦文. 有限球谐位场曲面延拓方法. 物探化探计算技术 , 1988, 10(3): 203–210. Liang J W. Surface continuation method of finite spherical harmonics for potential fields. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1988, 10(3): 203-210. |
| [6] | 安玉林, 谭宝华. 局部重磁场源全方位成像(计算地球物理丛书之三). 北京: 地质出版社, 1997 . An Y L, Tan B H. Omnidirectional Imagery of Local Gravity and Magnetic Anomaly Sources (Computing Geophysical Series (Third) (in Chinese). Beijing: Geological Publishing House, 1997 . |
| [7] | 王谦身, 安玉林, 张赤军, 等. 重力学(中国现代科学全书·固体地球物理学). 北京: 地震出版社, 2003 . Wang Q S, An Y L, Zhang C J, et al. Gravitology (Chinese Encyclopaedic Series of Modern Sciences Solid Geophysics) (in Chinese). Beijing: Seismological Press, 2003 . |
| [8] | 蔡宗熹. 曲面上的位场理论及其在地球物理中的应用(科学与工程计算丛书). 郑州: 河南科学技术出版社, 2002 . Cai Z X. Potential Field Theory on an Uneven Surface and Its Application in Geophysics (Science and Engineering Computing Series) (in Chinese). Zhengzhou: He'nan Science and Technology Press, 2002 . |
| [9] | Dampney C N G. The equivalent source technique. Geophysics , 1969, 34(1): 39-53. DOI:10.1190/1.1439996 |
| [10] | Bhattacharyya B K, Chan K C. Reduction of magnetic and gravity data on an arbitrary surface acquired in a region of high topographic relief. Geophysics , 1977, 42(7): 1411-1430. DOI:10.1190/1.1440802 |
| [11] | 周熙襄, 钟本善, 冯敬英. 用等效源法进行重磁异常换算的效果. 物探化探计算技术 , 1979, 1(1): 15–26. Zhou X X, Zhong B S, Feng J Y. The effect of transforming gravity and magnetic anomaly by using equivalent sources method. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1979, 1(1): 15-26. |
| [12] | Nakatsuka T. Reduction of magnetic anomalies to and from an arbitrary surface. Geophysical Exploration , 1981, 34(5): 6-12. |
| [13] | 杜维本. 三维重磁场曲化平的一个方法. 地球物理学报 , 1982, 25(1): 73–83. Du W B. A method for reduction of 3D gravity and magnetic fields on curved surface to a plane. Chinese J. Geophys. (in Chinese) , 1982, 25(1): 73-83. |
| [14] | 陈钟琦. 等效偶层法位场曲面延拓的原理和计算方法. 地球物理学报 , 1983, 26(1): 70–79. Chen Z Q. Principle and computational method of curved surface's continuation of potential field for equivalently dipolar layer's method. Chinese J. Geophys. (in Chinese) , 1983, 26(1): 70-79. |
| [15] | 候重初, 蔡宗熹, 刘魁俊. 从单层位出发建立曲面上的位场转换解释系统(一). 物化探计算技术 , 1985, 7(1): 1–12. Hou Z C, Cai Z X, Liu K J. Establishing an interpretation system of potential field transformation on an uneven surface from the potential of a single layer (First Part). Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1985, 7(1): 1-12. |
| [16] | 候重初, 蔡宗熹, 刘魁俊. 从单层位出发建立曲面上的位场转换解释系统(二). 物化探计算技术 , 1985, 7(2): 99–107. Hou Z C, Cai Z X, Liu K J. Establishing an interpretation system of potential field transformation on an uneven surface from the potential of a single layer (Second Part). Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1985, 7(2): 99-107. |
| [17] | 候重初, 蔡宗熹, 刘魁俊. 从偶层位出发建立曲面上的位场转换解释系统. 地球物理学报 , 1985, 28(4): 410–418. Hou Z C, Cai Z X, Liu K J. Interpretation system of potential field transformation on an uneven surface from the potential of a double layer. Chinese J. Geophys. (in Chinese) , 1985, 28(4): 410-418. |
| [18] | 管志宁, 安玉林, 陈维雄. 曲线与曲面上磁场向上延拓与分量转换. 地球物理学报 , 1985, 28(4): 419–428. Guan Z N, An Y L, Chen W X. Upward continuation and transformation of component of magnetic field on an undulating observed profile or surface. Chinese J. Geophys. (in Chinese) , 1985, 28(4): 419-428. |
| [19] | Starcevic M. Analysis of methods of reduction of the Bouguer anomaly to a horizontal plane and its application in regions of rugged topography. University of Belgrade, Belgrade, 1985. |
| [20] | Ivan M. Upward continuation of unevenly spaced potential field data using equivalent sources. Geophysical Transactions , 1986, 32: 31-42. |
| [21] | 蔡宗熹, 张培琴, 张庆合. 多重网格方法在求曲面位场等效源上的应用. 地质信息技术 , 1990(4): 69–74. Cai Z X, Zhang P Q, Zhang Q H. The multigrid method application in inversing equivalent sources of potential field on curved surface. DiZHiXinXiJiSHu (in Chinese) , 1990(4): 69-74. |
| [22] | 王万银, 潘作枢, 李家康. 三维高精度重磁位场曲面延拓方法. 物探与化探 , 1991, 15(6): 415–422. Wang W Y, Pan Z S, Li J K. Continuation methods for curved surface of the three-dimensional high-precision gravity and magnetic potential field. Geophysical and Geochemical Exploration (in Chinese) , 1991, 15(6): 415-422. |
| [23] | 潘作枢. 位场资料处理及解释问题. 北京: 地质出版社, 1992 . Pan Z S. The Problems for Data Processing and Interpretation of Potential Field (in Chinese). Beijing: Geological Publish House, 1992 . |
| [24] | 李家康. 有限元矩量法三维位场曲面延拓. 石油地球物理勘探 , 1992, 27(4): 482–492. Li J K. Curved surface continuation of three-dimensional potential field data by using finite element moment method. Oil Geophysical Prospecting (in Chinese) , 1992, 27(4): 482-492. |
| [25] | 蔡宗熹, 张培琴, 张庆合, 等. 二重网格方法用于曲面位场转换. 物探化探计算技术 , 1992, 14(4): 279–285. Cai Z X, Zhang P Q, Zhang Q H, et al. Twofold gridding method applied to the transformation of potential field on curved surface. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1992, 14(4): 279-285. |
| [26] | Ivan M. Upward continuation of potential fields from a polyhedral surface. Geophysical Prospecting , 1994, 42(5): 391-404. DOI:10.1111/gpr.1994.42.issue-5 |
| [27] | Henderson R G, Cordell L. Reduction of unevenly spaced potential field data to a horizontal plane by means of finite harmonic series. Geophysics , 1971, 36(5): 856-866. DOI:10.1190/1.1440220 |
| [28] | 王忠敏, 张培琴. 复杂磁异常若干处理方法. 物化探研究报导 , 1981(6). Wang Z M, Zhang P Q. Some disposal methods of complicated magnetic anomalies. Bulletin of Institute of Geophysical and Geochemical Prospecting (in Chinese) , 1981(6). |
| [29] | 何玉辉, 柳雪芬. 空间域重磁资料处理解释系统. 北京: 地质出版社, 1987 . He Y H, Liu X F. The disposal and Interpretation System for Gravity and Magnetic Data in Space Domain (in Chinese). Beijing: Geological Publish House, 1987 . |
| [30] | Grauch V J S.用泰勒级数展开式进行位场数据的曲化平或平化曲延拓.蔡宗熹译.地质信息技术, 1987, (3): 84-101. Grauch V J S. Transforming potential field values on uneven surface to horizontal plane or on horizontal plane to curved surface by using Taylor series expandedness. Translated by Cai Z X. DiZHiXinXiJiSHu (in Chinese), 1987, (3): 84-101. |
| [31] | Ivan M. On the upward continuation of potential field data between irregular surfaces. Geophysical Prospecting , 1986, 34(5): 735-742. DOI:10.1111/gpr.1986.34.issue-5 |
| [32] | Guspi F. Frequency-domain reduction of potential field measurements to a horizontal plane. Geoexpl. , 1987, 24(1): 87-98. |
| [33] | Pilkington M, Urquhart W E S. Reduction of potential field data to a horizontal plane of frequency domain for reduction to a plane using the potential field and its gradients. Computing Techniques for Geophysical and Geochemical Exploration , 1995, 17(4): 60-66. |
| [34] | Xia J H, Sprowl D R. Correction of topographic distortion in gravity data. Geophysics , 1991, 56(3): 537-542. |
| [35] | 候俊胜, 管志宁, 张自立. 综合利用位场及其梯度的频率域曲化平方法. 物探化探计算技术 , 1995, 17(4): 60–66. Hou J S, Guan Z N, Zhang Z L. Method of frequency domain for reduction to a plane using the potential field and its gradients. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1995, 17(4): 60-66. |
| [36] | 王万银, 潘作枢. 曲面位场数据处理及转换的三角函数法. 物探与化探 , 1997, 19(3): 209–218. Wang W Y, Pan Z S. The trigonometric function methods for data processing and transform of curved surface potential field. Geophysical and Geochemical Exploration (in Chinese) , 1997, 19(3): 209-218. |
| [37] | 数学手册编写组. 数学手册. 北京: 人民教育出版社, 1979 . Compilatory Group of Math Handbook. Math Handbook (in Chinese). Beijing: People's Education Press, 1979 . |
| [38] | 雷日克ИМ, 格拉德什坦ИС. 重要函数表和积分表. 北京: 人民教育出版社, 1959 . LeiRiK И М, Gradeshitan И С. Important Function and Integral Tabulation (in Chinese). Beijing: People's Education Press, 1959 . |
| [39] | 安玉林, 黄金明. 局部重磁场源全方位成像(续). 北京: 地震出版社, 2003 . An Y L, Huang J M. Omnidirectional Imagery of Local Gravity and Magnetic Anomaly Sources (Continuation) (in Chinese). Beijing: Seismological Press, 2003 . |
 2013, Vol. 56
2013, Vol. 56

