2. 东华理工大学核工程与地球物理学院, 南昌 330013
2. College of Nuclear Engineering and Geophysics, East China Institute of Technology, Nanchang 330013, China
应用位场数据识别地质体边界是地质解释的一项重要工作.位场异常中包含有场源边界的信息, 但边界信息的提取需要进行相关的数据处理.为此, 地球物理工作者提出了许多基于位场梯度的边界检测方法.这些方法按边界检测的计算模式, 可分为导数分析和数理统计两类[1].
导数分析法主要有垂向导数分析法[2]、水平总梯度[3]、tiltangle[4]及其水平总梯度[5]、Theta map [6]等方法.垂向导数分析法是Evjen提出的, 主要是利用垂向一、二阶导数的零值线确定地质体边界[2]; Cordell提出了水平梯度法, 利用水平梯度模极大值检测场源边界[3]; 这两种方法有效地提高了对原异常信息的识别能力, 但难以同时反映出深度不同的地质体边界[7]. Miller等提出了tiltangle法, 该法识别地质体边界的原理与垂向导数类似[4]; Verduzco在tiltangle法基础上提出了tiltangle水平总梯度法, 用计算结果的极大值检测地质体边界, 但在计算过程中采用了异常的二阶导数, 更易受高频干扰的影响[5]. Wijns等采用水平总梯度与一阶解析信号比值(Thetamap)来分析磁源边界, 对低纬度磁性体有较好的边界检测能力, 但检测的边界与深部地质体的实际边界位置有偏差[6].
数理统计法主要有Euler反褶积[8-10]、小子域滤波[11]、导数归一化标准差[12]、均方差比归一化垂向梯度[13]等方法. Euler反褶积法是将位场异常和其梯度联系在一起的Euler齐次方程, 该方法可用于地质体边界的识别, 但方程式灵敏度较高, 导数计算结果稍有偏差, 便会在计算结果中产生较大的偏离, 从而影响反演的精度[14].小子域滤波法是杨高印针对异常分离提出的, 可用于边界的识别, 但只对原异常中以梯级带形式显示的边界位置有效[11]; 张凤旭等[15-16]在小子域滤波基础上, 提出了三方向小子域滤波法, 获得了较为详细的断裂构造信息, 但计算结果与实际地质体边界也有一定的偏差. Cooper等[12]借助于异常导数的标准差, 提出了可以检测不同深度地质体边界的归一化标准差法; 王彦国等[13]在2012年提出了均方差比归一化垂向梯度的边界检测方法, 对不同深度的地质体边界也有较好的探测效果, 但这两种方法在计算的过程中同样采用了导数计算, 因此也会受噪声等高频干扰.
显然, 上述边界检测方法大都是以位场梯度计算为基础的, 方法运算简单, 物理意义也明确, 但在实际资料处理中都存在着受高频干扰的影响[14].在处理这个问题上, 如果直接采用低通滤波进行降噪, 则会损失部分有用信号.
在利用位场异常进行场源边界识别中, 一阶导数分析是目前常用的一类方法.不过笔者认为, 导数的阶次越高, 对场源的边界识别能力和定位精度就越强, 然而高阶导数易受噪声等干扰的影响, 而且导数的阶次越高, 高频干扰的影响就越为严重.如果能采用某种数学处理手段, 既能尽量减少导数异常中有效边界信息的损失, 又具有抗干扰能力的话, 势必可以提高场源的边界识别能力.为此, 本文提出了位场垂向梯度最佳自比值的边界检测方法.
2 方法原理分析 2.1 自比值的定义对于位场异常数据f(i, j), 设其垂向m阶导数为fz(m), 那么可以将导数异常fz(m)窗口内数据的均值与其均方根的比值定义为fz(m)的一次自比值κ, 即
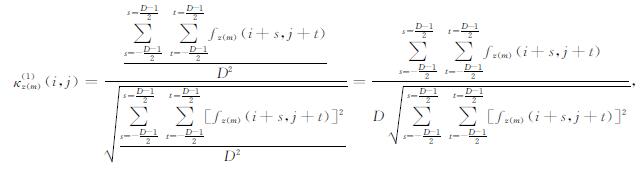
|
(1) |
式中: (i, j)为数据平面坐标点位, D为计算窗口长度.
由公式(1)可以看出, 自比值κz(m)(1)是在导数异常fz(m)窗口内平均化的处理结果, 因此, 其可以在一定程度上消除随机干扰.然而, 当导数阶次较高或原始异常f中含噪声较大时, 一次自比值κz(m)(1)消除噪声的能力往往是有限的, 因此需要更多次的自比值运算来进一步消除噪声的影响. fz(m)的n次自比值κz(m)(n)可由一次自比值κz(m)(1)逐次递推得到:
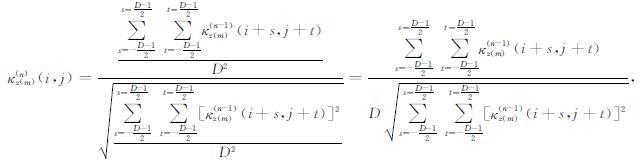
|
(2) |
当n=1时, 公式(2)中的κz(m)(0)=fz(m).
2.2 自比值数值分析构造如下二次函数Fij(x):

|
(3) |
由于开口向上的二次函数Fij(x)≥0对一切x∈ R恒成立, 故其判别式Δ≤0, 即
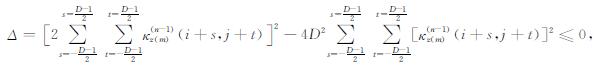
|
(4) |
则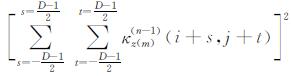
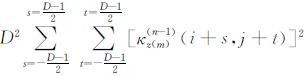
设垂向导数fz(m)在所选定的计算窗口内数据平均值为:
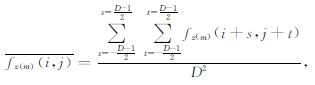
|
(5) |
则公式(1)可以重新写为:
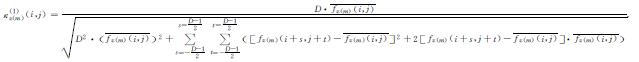
|
(6) |
当位场梯度数据fz(m)远离场源边界位置时, 异常梯度变化平缓, 窗口内的数据均趋于均值, 也就是上述公式中的(fz(m)(i+s, j+t)-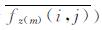
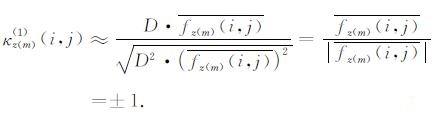
|
(7) |
而当fz(m)在场源边界附近时, 异常梯度大, 且均值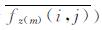

|
(8) |
依据以上分析知:当fz(m)远离地质体边界位置时, 一次自比值κz(m)(1)趋于±1;当fz(m)在地质体边界位置时, κz(m)(1)则趋近于0.
由于n次自比值κz(m)(n)是在n-1次自比值κz(m)(n-1)的基础上获得的进一步归一化结果(公式(2)).因此, 当自比值的次数等于n时, κz(m)(n)与n-1次自比值κz(m)(n-1)相比, 在场源边界位置表现的梯级带特征会更明显, 数值也会更趋近于0, 即κz(m)(n)

依据文献[17-19], 可定义垂向m阶导数的第n次自比值与第n+1次自比值的归一化互相关系数R为:
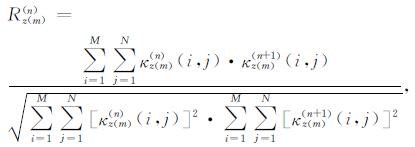
|
(9) |
其中M、N分别为测线数和每条测线的测点数.
事实上, 在选定的窗口下, 计算的自比值互相关系数与自比次数的关系曲线中存在一个明显极大值(后文将进一步阐述), 现将这个极大值点对应的自比次数定义为最佳次数, 将该次数对应的自比值称为最佳自比值.
由于在选定的初始窗口下, 最佳自比值未必是确定地质体边界位置的最佳结果, 因此需要选择最佳窗口的长度.最佳窗口长度的选取方案是:首先设定一个置信度R0(其取值一般介于0. 96和0. 99之间), 如果在初始窗口下, 自比值互相关系数的极大值max (R)大于给定的置信度R0, 则认为最佳自比值去噪能力强, 结果是可信的, 那么初始窗口即为最佳窗口; 若max (R)不大于R0, 则认为初始窗口下的自比值结果可信度较低, 需调整计算窗口的长度, 重新计算自比值互相关系数与自比次数的关系, 直到某一窗口下满足max (R) > R0时, 终止计算, 这时所对应的窗口大小便是最佳计算窗口长度.
2.5 最佳自比值计算步骤由以上分析知, 本文提出的垂向梯度最佳自比值法在给定置信度R0之后, 可以自适应地寻找到最佳窗口下的最佳自比次数, 然后通过最佳自比值进行场源边界的识别.为了方便起见, 在此给出算法的步骤:
(1) 采用快速傅里叶变换计算位场数据的垂向梯度fz(m);
(2) 给定初始窗口长度(一般选取D=5), 利用公式(1)和(2)计算fz(m)的n次自比值κz(m)(n);
(3) 根据公式(9)计算自比值的互相关系数Rz(m)(n);
(4) 给定置信度R0, 将初始窗口下的互相关系数极大值max (R)与R0进行比较.若max (R) > R0, 则输出最佳自比值; 若max (R)≤R0, 则调整窗口长度, 重新计算(2)、(3)步骤, 直到满足max (R) > R0为止.
值得说明的是:为了进一步提高地质体边界的定位精度, 可采用杨高印提出的小子域滤波[11]对最佳自比值进行滤波输出.
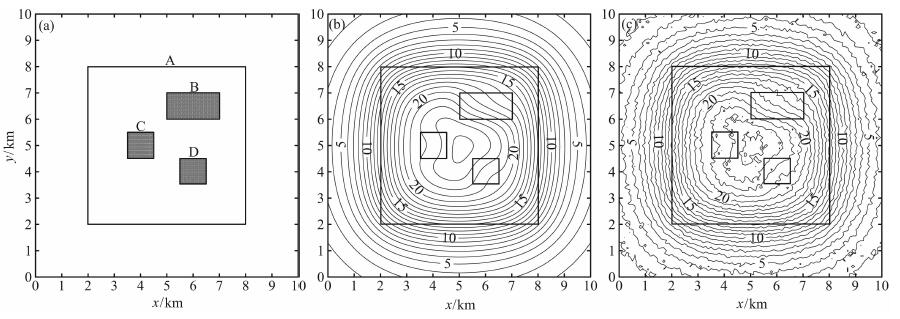
3 理论模型分析为了验证本文方法的边界识别能力, 设计了一个包含4个不同参数的长方体组合模型(模型体参数见表 1, 位置见图 1a), 其产生的理论重力异常见图 1b.同时为了验证方法消除噪声的能力, 在叠加模型体产生的重力异常中加入了随机噪声(图 1c).
|
|
表 1 模型参数 Table 1 The model parameters |
|
图 1 (a) 模型体平面示意图; (b) 理论模型重力异常(单位: 10-6m/s2); (c) 加3%随机噪声的重力异常(单位: 10-6m/s2) Fig. 1 (a) Combinatorial models′ location; (b) Forward gravity anomaly (unit: 10-6m/s2); (c) Adding 3% random noise to forward gravity anomaly (unit: 10-6m/s2) |
从模型重力异常(图 1b)中可以看出, 地质体A由于埋深和规模较大, 其产生的异常在边界位置表现出的梯级带范围较宽, 因此利用该异常所显示的边界特征是无法精确确定地质体边界位置的; 地质体B、C、D规模较小, 受地质体A的影响, 其产生的异常在叠加异常中表现为等值线同形扭曲, 显然只依靠这种异常特征难以确定出这三个地质体的边界; 而且在加入噪声后, 异常图(图 1c)在三个地质体位置所显示的等值线同形扭曲特征变的模糊不清, 这进一步增加了边界识别的难度.
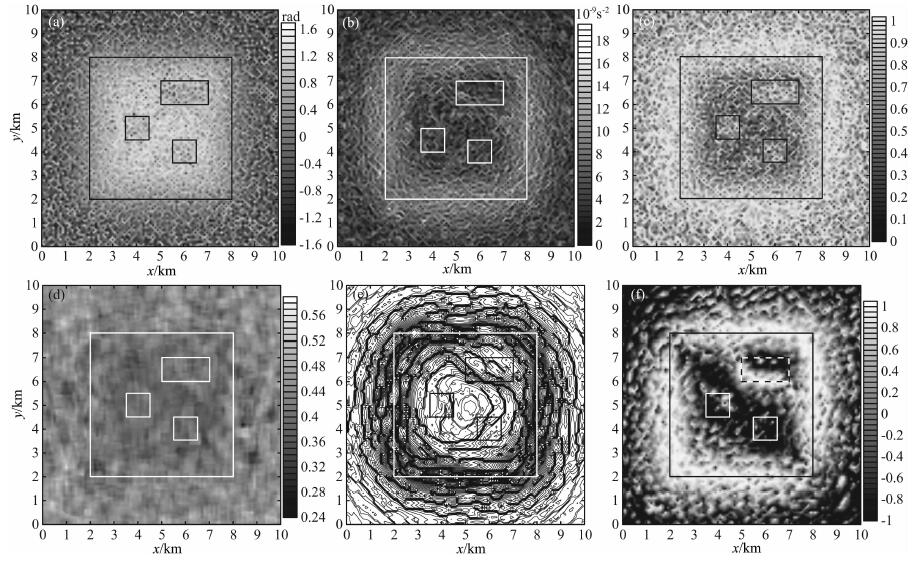
在模型试验中, 笔者先用tiltangle、水平总梯度、Thetamap、导数归一化标准差、小子域滤波和均方差比归一化垂向梯度6种已有的边界识别方法对含噪声的重力异常分别进行了计算.各种方法计算的结果见图 2, 从中可以看出, 由于受噪声和异常叠加的影响, 6种方法的计算结果均无法清晰地显示模型体A的边界, 更无法有效地识别其它3个较小模型体的边界.
|
图 2 常规边界识别方法计算结果 (a) tilt angle; (b) 水平总梯度; (c) Thetamap; (d) 导数归一化标准差(计算窗口5×5);(e) 小子域滤波; (f) 均方差比归一化垂向梯度. Fig. 2 The results of edge recognition using traditional methods (a) Tilt angle; (b) The horizontal total gradient; (c) Theta map; (d) Normalized standard deviations (window size of 5×5); (e) Small subdomain filtering; (f) Normalized vertical gradient of mean square error ratio. |
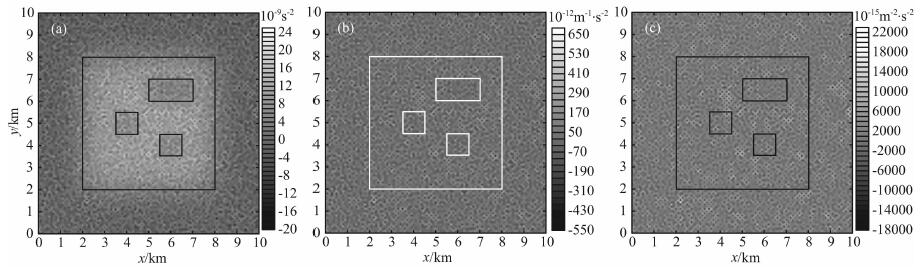
接着计算了含噪声重力异常垂向一阶、二阶和三阶导数(图 3).图中可见, 垂向一阶导数(图 3a)还能模糊地识别出地质体A的边界; 而垂向二阶导数(图 3b)和垂向三阶导数(图 3c)由于干扰放大严重, 有用信号完全淹没在噪声中.
|
图 3 含噪声重力异常垂向导数 (a) 垂向一阶导数;(b) 垂向二阶导数;(c) 垂向三阶导数. Fig. 3 Vertical derivatives of gravity anomaly including random noise (a) First-order vertical derivative; (b) Second-order vertical derivative; (c) Third-order vertical derivative. |
最后对含噪声的重力异常垂向一、二、三阶导数进行了最佳自比值的分析和计算.在计算最佳自比值之前, 首先需确定自比值计算的最佳窗口和最佳自比次数.这两个参数可以在图 4所示的自比值互相关系数与自比次数的关系曲线中分析确定.

|
图 4 自比值互相关系数与自比次数的关系曲线 Fig. 4 The relationship of cross-correlation coefficient of two successive auto-ratios and the number of auto-ratio |
从图 4中可以看出, 无论是哪一阶垂向导数, 其自比值的互相关系数均随着自比次数的增加而先增大后减小, 存在着一个明显的极大值点.大量的模型试验表明, 该极值点就是确定最佳窗口大小和自比次数的重要依据.
在计算最佳窗口和最佳自比次数(图 4)时, 首先选择初始窗口D=5, 由于该窗口条件下垂向一阶和二阶导数的自比值互相关系数极大值均大于可信度R0(文中选取R0=0. 98), 因此可确定垂向一阶、二阶导数的最佳窗口与初始窗口相同(D=5), 相对应的最佳自比次数分别为n=3和n=4.对于垂向三阶导数, 由于在初始窗口下的互相关系数极大值max (Rz(3))=0. 956, 小于R0, 因此将计算窗口长度增加至D=7, 此窗口下的max (Rz(3))=0. 994, 大于R0, 即垂向三阶导数自比值的最佳窗口为D=7, 其对应的最佳自比次数为n=4.
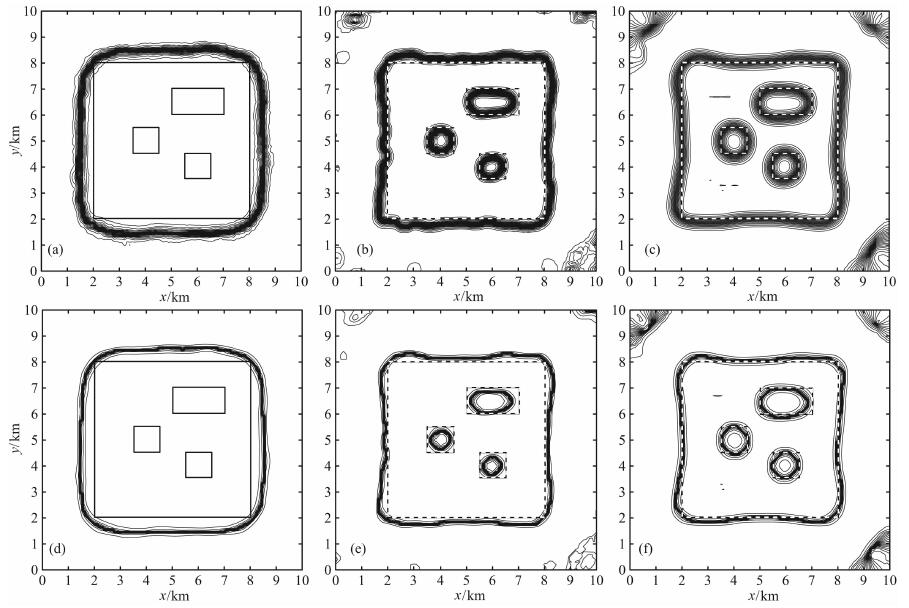
利用上述最佳窗口和最佳自比次数计算的最佳自比值结果见图 5.由图可见, 垂向一、二、三阶导数的最佳自比值(图 5a-5c)均有效地消除了噪声干扰的影响.一阶导数最佳自比值(κz(1)(3)|D=5)将模型A的边界较好地反映出来, 但识别的边界与模型实际边界位置存在较大的偏差, 而且无法识别出其它三个地质体, 这说明垂向一阶导数对边界的识别能力有限; 垂向二阶导数最佳自比值κz(2)(4)|D=5可以较好地检测出所有模型体的边界, 边界的定位精度相对于κ (3) z(1)|D=5也有了较大的提高, 但检测到的边界与地质体边界仍有偏差; 垂向三阶导数最佳自比值κ (4) z(3)|D=7不仅反映出了所有地质体的边界, 而且异常梯级带与场源边界有着较好的对应关系.三个垂向导数最佳自比值的小子域滤波结果(图 5d-5f)对相应最佳自比值的梯级带均进行了较好的紧缩, 可以更精确地检测出地质体的边界.
|
图 5 最佳自比值及其小子域滤波结果 (a)、(b)、(c)分别是垂向一、二、三阶导数的最佳自比值;(d)、(e)、(f)分别是图 5a、5b、5c的小子域滤波. Fig. 5 Optimal auto-ratios and their small subdomain filtering (a), (b) and (c) are optimal auto-ratios of firs-, second-, third-order vertical derivative, respectively; (d), (e) and (f) are results of small subdomain filtering of Fig. 5a, 5b and 5c, respectively. |
以上对比分析充分证明, 本文提出的边界检测方法不但具有较高的精度, 而且计算过程更为稳定.
4 实际重力资料1)应用1) 实际资料来源于中国石油天然气股份有限公司吉林分公司(吉林油田).
为了验证垂向梯度最佳自比值对实际资料的处理效果, 选取了吉林省南部鸭绿江盆地2)实测重力数据进行试验.
2) 鸭绿江盆地是2007年吉林油田为了拓展油气勘探新领域, 开展吉林探区外围盆地战略选取工作时提出的, 并初步认为该盆地是一个值得勘探的新探区、新领域和新层系.
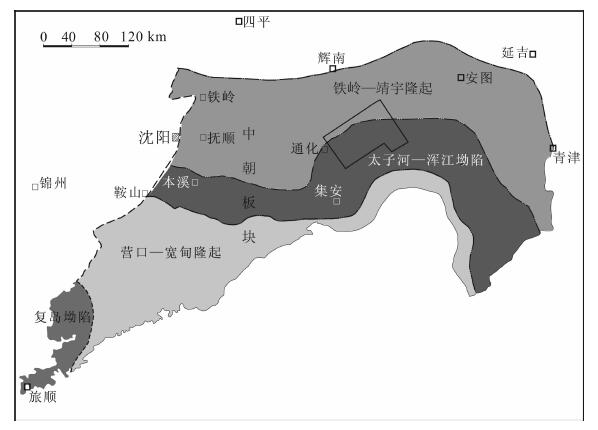
鸭绿江盆地位于中朝板块东北缘, 二级大地构造单元隶属于辽东台隆区, 主体位于太子河-浑江坳陷内(图 6).在盆地内, 除志留纪、泥盆纪和早石炭世地层缺失外, 其它时代的地层均有出露(图 7), 而且不同时代的地层间接触关系较为复杂, 这给地质体边界的确定带来了较大难度, 不过研究区内各个时代的岩石出露较好, 这也为方法试验的可靠性提供了较好的对比依据.
|
图 6 鸭绿江盆地区域构造位置图(方框为研究区) Fig. 6 Regional-position map of Yalujiang basin (study area in square frame) |

|
图 7 鸭绿江盆地地质图 Fig. 7 Geology map of Yalujiang basin |
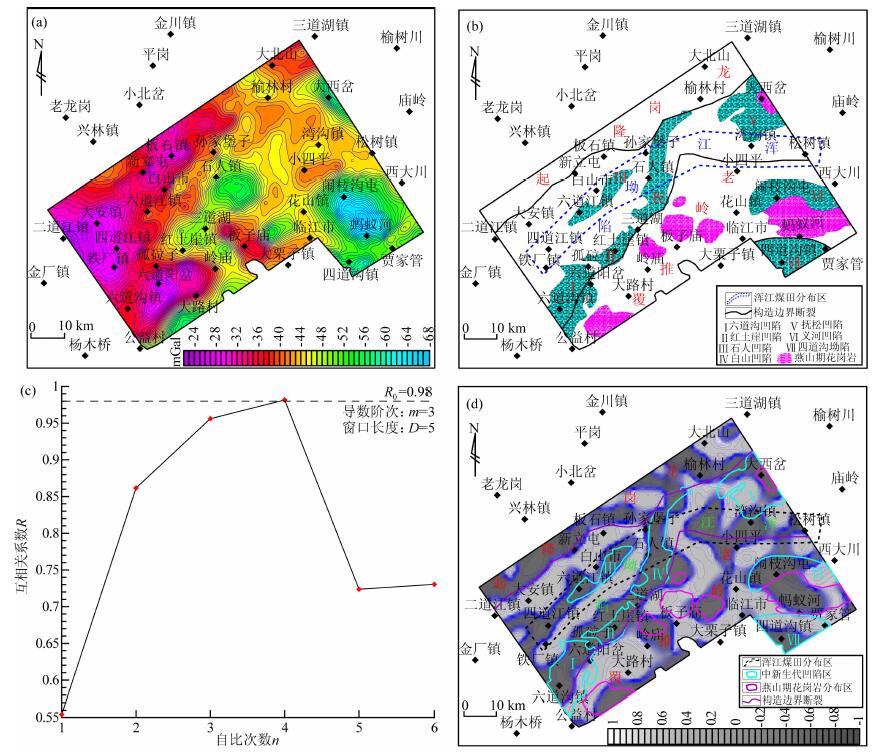
从研究区布格重力异常(图 8a)中可以看出, 反映地质体边界位置或断裂构造的梯级带主要分布在二道江-新立屯-板石镇一线、四道江-六道江-白山-孙家堡子一线、孤砬子-红土崖-三道湖-石人一线、公益村-大路村一线以及蚂蚁河-闹枝沟屯圈闭区等位置, 这几组异常梯级带可能是大型地质体边界(或规模较大的断裂构造)的反映.但这些异常梯度带较平缓, 边界位置难以直接从重力异常图中精确定位.另外, 较小型地质体边界受区域异常影响较大, 在异常图中主要表现为异常等值线突然变宽或变窄以及同形扭曲等非梯级带特征, 这类地质体边界位置确定难度更大.
|
图 8 (a) 鸭绿江盆地布格重力异常(单位10-5m • s-2); (b) 研究区构造分区图; (c)垂向三阶导数自比值互相关系数与自比值次数关系曲线; (d)垂向三阶导数最佳自比值 Fig. 8 (a) Bouguer gravity anomaly of Yalujiang basin (unit: 10-5m • s-2); (b) The tectonic division of research area; (c) The relationship of cross-correlation coefficient of two successive auto-ratios of third-order vertical derivative and the number of auto-ratio; (d) Optimal auto-ratio of third-order vertical derivative |
图 8b为结合区域地质和前人地质-地球物理工作成果勾划的构造分区图3).图中给出的大型断裂位置、燕山期花岗岩出露区、中新生代凹陷分布范围以及浑江煤田工作区等信息, 可为文中方法的有效性提供佐证.
3) 刘财, 张凤旭.吉林省南部重磁资料处理与解释(成果报告).吉林大学, 2011.
图 8c为研究区垂向三阶导数自比值互相关系数与自比次数的关系曲线, 仿照图 4做法, 可检测出最佳窗口长度D=5和最佳自比次数n=4, 进而获得了垂向三阶导数最佳自比值的计算结果(图 8d).从中可以看出, 最佳自比值不仅清晰地反映出龙岗隆起和浑江坳陷之间以及浑江坳陷和老岭推覆区之间的大型断裂, 还较好地显示出了不同岩性间的接触带(图 7).另外, 自比值圈定的负异常较好地反映出了研究区中-新生代地层和燕山期花岗岩等相对低密度岩石的分布, 也客观地反映出了浑江煤田的工作范围.这些结果与已知地质资料以及前人的工作成果符合较好, 有力地佐证了方法的有效性.
5 结论有效地利用位场相应阶次的导数异常, 能够提高地质构造解释的分辨率, 但高阶导数换算对干扰的放大作用一直困扰着地球物理工作者.本文在前人工作的基础上, 另辟蹊径, 提出了位场垂向梯度最佳自比值的边界检测方法.在文中, 笔者对方法进行了数值分析, 并阐述了该算法检测地质体边界的物理机制.模型试验和实际算例表明, 垂向梯度最佳自比值算法不但能够有效地消除导数中的干扰成分, 而且能够精细地识别出地质体的边界.
本文实现了高阶导数在位场边界识别中的应用.由于自比值可以有效地压制干扰, 因此可以提供更丰富、精确的边界信息, 为高阶导数在位场数据处理中的有效应用提供了新的思路.
| [1] | 王万银, 邱之云, 杨永, 等. 位场边缘识别方法研究进展. 地球物理学进展 , 2010, 25(1): 196–210. Wang W Y, Qiu Z Y, Yang Y, et al. Some advances in the edge recognition of the potential field. Progress in Geophys. (in Chinese) , 2010, 25(1): 196-210. |
| [2] | Evjen H M. The place of the vertical gradient in gravitational interpretations. Geophysics , 1936, 1(1): 127-136. DOI:10.1190/1.1437067 |
| [3] | Cordell L. Gravimetric expression of graben faulting in Santa Fe Country and the Espanola Basin. New Mexico: New Mexico Geol. Soc. Guidebook, 30th Field Conf., 1979: 59-64. |
| [4] | Miller H G, Singh V. Potential tilt-A new concept for location of potential field sources. Journal of Applied Geophysics , 1994, 32(2-3): 213-217. DOI:10.1016/0926-9851(94)90022-1 |
| [5] | Verduzco B, Fairhead J D, Green C M, et al. New insights into magnetic derivatives for structural mapping. The Leading Edge , 2004, 23(2): 116-119. DOI:10.1190/1.1651454 |
| [6] | Wijns C, Perez C, Kowalczyk P. Theta map: edge detection in magnetic data. Geophysics , 2005, 70(4): 39-43. DOI:10.1190/1.1988184 |
| [7] | Cooper G R J. Balancing images of potential-field data. Geophysics , 2009, 74(3): L17-L20. DOI:10.1190/1.3096615 |
| [8] | Thompson D T. EULDPH: A new technique for making computer-assisted depth estimates from magnetic data. Geophysics , 1982, 47(1): 31-37. DOI:10.1190/1.1441278 |
| [9] | Reid A B, Allsop J M, Granser H, et al. Magnetic interpretation in three dimensions using Euler deconvolution. Geophysics , 1990, 55(1): 80-91. DOI:10.1190/1.1442774 |
| [10] | Hansen R O, Laura S. Multiple-source Euler deconvolution. Geophysics , 2002, 67(2): 525-535. DOI:10.1190/1.1468613 |
| [11] | 杨高印. 位场数据处理的一项新技术--小子域滤波法. 石油地球物理勘探 , 1995, 30(2): 240–244. Yang G Y. A new technique for potential-field data processing: small subdomain filtering. Oil Geophysical Prospecting (in Chinese) , 1995, 30(2): 240-244. |
| [12] | Cooper G R J, Cowan D R. Edge enhancement of potential-field data using normalized statistics. Geophysics , 2008, 73(3): 1-4. |
| [13] | 王彦国, 王祝文, 张凤旭, 等. 基于均方差比归一化垂向梯度法的位场边界检测. 中国石油大学学报(自然科学版) , 2012, 36(2): 86–90. Wang Y G, Wang Z W, Zhang F X, et al. Edge detection of potential field based on normalized vertical gradient of mean square error ratio. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2012, 36(2): 86-90. |
| [14] | 张恒磊, 刘天佑, 杨宇山. 各向异性标准化方差计算重磁源边界. 地球物理学报 , 2011, 54(7): 1921–1927. Zhang H L, Liu T Y, Yang Y S. Calculation of gravity and magnetic source boundary based on anisotropy normalized variance. Chinese J. Geophys. (in Chinese) , 2011, 54(7): 1921-1927. |
| [15] | 张凤旭, 张凤琴, 刘财, 等. 断裂构造精细解释技术--三方向小子域滤波. 地球物理学报 , 2007, 50(5): 1543–1550. Zhang F X, Zhang F Q, Liu C, et al. A technique for elaborate explanation of faulted structures: three-directional small subdomain filtering. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1543-1550. |
| [16] | 张凤旭, 张兴洲, 张凤琴, 等. 中国东北地区重力场研究--利用改进的三方向小子域滤波划分主构造线及大地构造单元. 地球物理学报 , 2010, 53(6): 1475–1485. Zhang F X, Zhang X Z, Zhang F Q, et al. Study of gravity field in Northeastern China area: Classification of main structure lines and tectonic units using the improved three-directional small subdomain filtering. Chinese J. Geophys. (in Chinese) , 2010, 53(6): 1475-1485. |
| [17] | 高光珠, 李忠武, 余理富, 等. 归一化互相关系数在图像序列目标检测中的应用. 计算机工程与科学 , 2005, 27(3): 38–40. Gao G Z, Li Z W, Yu L F, et al. Application of the normalized cross correlation coefficient in image sequence object detection. Computer Engineering and Science (in Chinese) , 2005, 27(3): 38-40. |
| [18] | 曾华霖, 许德树. 最佳向上延拓高度的估计. 地学前缘 , 2002, 9(2): 499–504. Zeng H L, Xu D S. Estimation of optimum upward continuation height. Earth Science Frontiers (in Chinese) , 2002, 9(2): 499-504. |
| [19] | 孟小红, 刘国锋, 陈召曦, 等. 基于剩余异常相关成像的重磁物性反演方法. 地球物理学报 , 2012, 55(1): 304–309. Meng X H, Liu G F, Chen Z X, et al. 3-D gravity and magnetic inversion for physical properties based on residual anomaly correlation. Chinese J. Geophys. (in Chinese) , 2012, 55(1): 304-309. |
 2013, Vol. 56
2013, Vol. 56



