2. 中国科学院大学, 北京 100049;
3. 山东科技大学地质科学与工程学院, 青岛 266590
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. College of Geological Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China
地震波通过一组薄互层,其振幅、相位等会发生变化,这种现象称为地层滤波现象.地层滤波对后续处理和解释(如AVO反演等)带来很大的偏差,甚至影响地震波的分辨率和信噪比,因此引起了人们对地层滤波的广泛关注及其消除技术的深入研究.其研究包括差分法和积分法两个方面.
差分法即Goupillaud层方法[1],该方法利用层状介质中的能流关系以及上下行波的运动学公式推导了一维情况下的能流守恒方程,此方程揭示了反射波场与预测算子(透射波频谱倒数)之间的关系,并且通过Levinson递归方程把预测算子与反射系数序列联系起来,但由Levinson算法反求地层反射系数时需要逐层递推,运算量大,且很难针对某一深度直接计算,当阶数高时稳定性差,同时会伤害有效波.
Liu[2]等人通过物理实验与数值模拟详细研究了入射波波长对不同地层厚度的地层滤波关系,但对于如何消除薄层间的多重散射,没有给出具体的方法.
最早提出的地层滤波积分解是O′Doherty-Anstey公式[3],即地层透射波的频谱的对数等于反射系数的功率谱,其物理意义较为简明.最初,该积分解表达式是从数值结果发现的.目前消除地层滤波效应主要利用地层滤波积分解或者等效解的表达式,采取Q值补偿.由于O′Doherty-Anstey公式便于消除地层滤波效应,因此很多人试图对其进行严格证明,Banik(1986)[4]、Shapiro(1993)[5]、Matthew(2005)[6]等人分别采用统计理论、自平均及局域化波的概念、辐射传递理论来证实该公式,Shapiro等人将该公式推广到了斜入射情况.但这些证明难以导出高阶修正项,因此对于反射系数较大的情况,该公式求取透射波频谱精度会存在误差.刘洪[7]等基于预测算子的指数映射表达式和李代数积分证明了该公式,并给出了高阶表达式,同时推广到了斜入射和横向变速情况.
Q值补偿经常存在不稳定问题,且会加强高频噪音[8-9],因此利用对积分解的认识发展新的消除地层滤波的方法十分重要,为此,本文对地层滤波李代数积分解开展了进一步研究,以便更稳定、快速、有效地消除地层滤波效应.
李代数积分法来源于保结构算法的思想[10-11],数学上的“结构”指的是内积、外积或者行列式,保结构就是使得解在变换中保持内积、外积或者行列式,在地层滤波中,保结构就是能流守恒.保结构算法的重要分支是在李代数域求解微分方程.李代数和李群都是算子(或者矩阵)的集合(或者域),李代数集合中的元素是李群集合中的元素的对数.如果在李代数域求解方程,则元素的e指数映射所得元素一定是在群上,因而一定保“结构”.Magnus(1954)发现了将李群元素所满足的微分方程转化为李代数域元素所满足的微分方程的方法,称为微分方程e指数解方法,该方法导出的方程称为Magnus方程.用数值方法和积分方法求解Magnus方程分别称为李群算法和李代数积分法.目前,李代数积分法已在地震走时计算[12]、速度分析[13]、波场延拓[14]等方面得到了应用,并较好地解决了复杂介质横向变速的问题[15].本文进一步推广了李代数积分在地震学领域的应用:首先介绍了O′Doherty-Anstey公式的高阶李代数积分表示,然后提出了基于李代数积分的Picard迭代算法(本文简称李代数反演)由预测算子得到反射系数序列,同时对不同阶李代数反演效率和效果进行了分析,最后展开了模型试验和实际数据处理.
2 方法原理 2.1 李代数积分介绍根据微分方程e指数解方法[16],方程
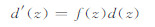
|
(1) |
的解d(z)满足
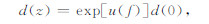
|
(2) |
其中,d(z)是函数,f和u(f)是算子,u(f)称为算子f的Lie代数积分或Lie代数解,满足如下Lie代数微分方程:
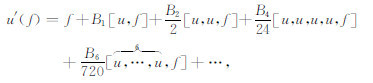
|
(3) |
式中Bn为Bernoulli数,即B0=1,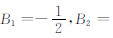
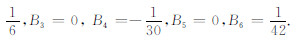
利用递推算法可知Lie代数微分方程的Lie代数积分解为
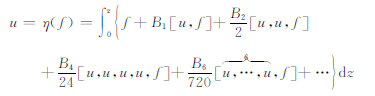
|
(4) |
其中,η为Lie代数积分运算.
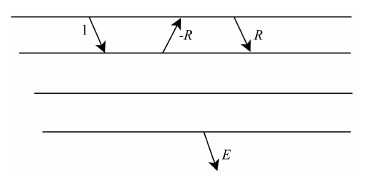
2.2 能流守恒方程与预测算子频谱的李代数积分表达如图 1所示,能流守恒方程[1]表明在不考虑地层吸收的情况下,顶层的地震波能流和下半空间的能流是一样的,公式表达如下:
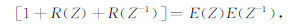
|
(5) |
|
图 1 观测模型 Fig. 1 The geometry model |
其中,R表示包括有效波和多次波在内的地震波场,E代表透射波;Z为传播算子,斜入射时表达式如下:
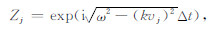
|
(6) |
式中,i为虚数单位,ω为圆频率,k为波数,vj为层速度,Δt为地层内的双程走时.垂直入射时(6)式可简单地表示为:
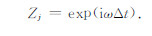
|
(7) |
令
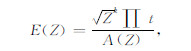
|
(8) |
则(5)式改写为:
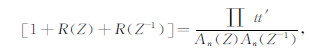
|
(9) |
A(Z)即为预测算子(或称自回归算子),t,t′为每层对应的透射系数,t=1+c,t′=1-c,c为每层的反射系数.一般情况下,c≪1,所以Πtt′ ≈1.通过(9)式,我们将地震波场和预测算子联系起来,因此,通过预测算子,可以快速得到地震波场.一维情况下,预测算子与反射系数的关系可由Levinson递归方程[1]给出:
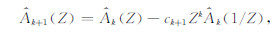
|
(10) |
进一步地,二维情况下,预测算子满足如下关系[7]:
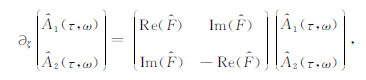
|
(11) |
其中,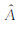
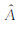
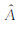
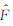
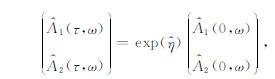
|
(12) |
其中,
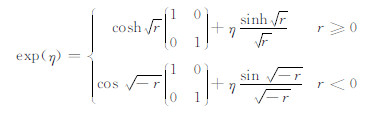
|
(13) |
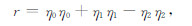
|
(14) |
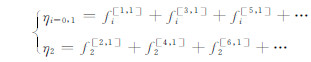
|
(15) |
公式(15)中上标表示李代数阶数,[1, 1]代表一阶,[3, 1]代表三阶,[5, 1]代表五阶.在实际运算中,fi[1, 1]对ηi贡献最大,其它高阶项都是对fi[1, 1]的校正.由于反射系数一般很小,数值上有:fi[1, 1]≫ fi[3, 1]≫fi[5, 1];η2为等效延迟修正.对于水平层状介质,由公式(4)可得公式(15)中各分量与反射系数的具体关系[7]如下:
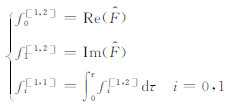
|
(16) |
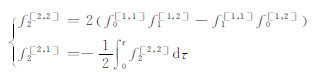
|
(17) |
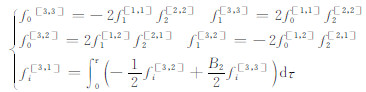
|
(18) |

|
(19) |
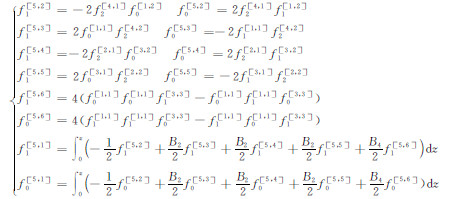
|
(20) |
基于上述关系,预测算子的表示如下:
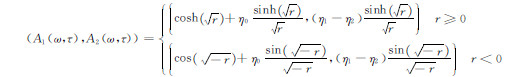
|
(21) |
公式(21)中可以看出,如果η0η0 +η1η1 -η2η2≥0,则(A1(ω,τ),A2(ω,τ))是正实函数,因而是可逆的;如果(η0,η1-η2)是因果信号频谱,则它在上半平面解析,因而可推得(A1(ω,τ),A2(ω,τ))-1也是因果信号频谱.由(21)式得预测算子功率谱:
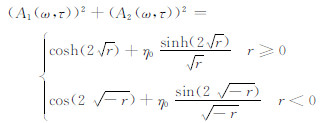
|
(22) |
(22)式即为O′Doherty-Anstey公式的高阶表达,公式(6)说明该公式也适合斜入射的情况.如果仅保留(15)式中的第一项fi[1, 1],可得O′Doherty-Anstey公式:
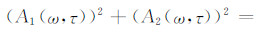
|
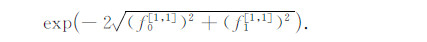
|
首先由地震波场求取透射波,对于测井VSP地震勘探,可以直接得到透射波记录,然后由透射波根据公式(8)得到预测算子频谱;对于一般的地震波场,可以根据谱分解方法由公式(9)得到预测算子频谱[1],去掉子波效应,得到反射系数对应的预测算子频谱.
基于(11)式,我们可以采用Picard迭代算法简单由预测算子得到反射系数序列,迭代步骤如下:
(1)令r=A12 +A22,计算η0,η1的初始值,
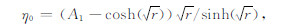
|
(23) |
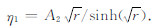
|
(24) |
(2)将η0,η1代入公式(21),计算得到A′1,A′2,令ΔA1=A1 -A′1,ΔA2=A2 -A′2;
(3)由ΔA1,ΔA2计算Δr,由公式(23),(24)计算η0,η1的增量Δη0,Δη1,对η0,η1进行校正:η0=η0 +Δη0,η1=η1 +Δη1;
(4)重复步骤(1)-(3),直到Δ|r| < ε结束,ε为一很小的数值.然后由η0,η1计算反射系数.对于比较复杂的反射系数,李代数积分一般取到五阶即可.
对于二维或三维炮集记录,可先对炮集记录进行τ-p变换,然后对每个p道进行多重散射消除,最后进行τ-p反变换得到消除薄层多重散射后的炮集数据.
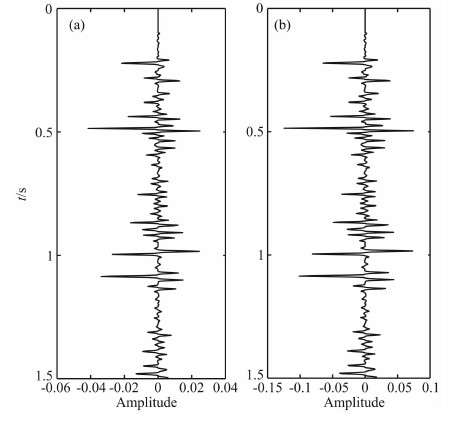
3 数值模拟 3.1 李代数积分求透射波频谱精度验证为了验证李代数积分方法求取透射波频谱的正确性,分别比较了一维情况下小反射系数(图 2a)和较大反射系数(图 2b)的透射波频谱,以Levinson递归算法求取的结果为对照标准.
|
图 2 (a)小反射系数时间序列;(b)较大反射系数时间序列 Fig. 2 (a) Small reflection coefficient series; (b) Big reflection coefficient series |
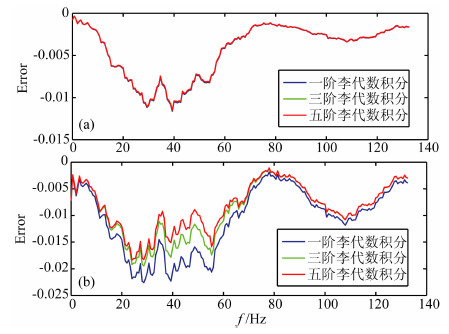
图 3a和3b分别为图 2a和2b所示的反射系数序列对应的透射波频谱误差曲线,蓝线、绿线和红线分别为采用一阶李代数积分(O′Doherty-Anstey公式)、三阶李代数积分以及五阶李代数积分计算的透射波频谱与Levinson递归算法求取的透射波频谱的差值曲线.可以看出,当反射系数较小时,一阶、三阶、五阶李代数积分算法得到的透射波频谱相差很小;当反射系数较大( > 0.1)时,五阶李代数积分得到的透射波频谱最接近真实值,而O′Doherty-Anstey公式得到的透射波频谱误差相对较大.
|
图 3 (a)小反射系数情况下不同阶李代数积分求取的透射波频谱误差曲线;(b)较大反射系数情况下不同阶李代数求取的透射波频谱误差曲线 Fig. 3 (a) Small reflection coefficient series' error curves of transmitted wave spectrum got by different order Lie algebra; (b) Big reflection coefficient series' error curves of transmitted wave spectrum got by different order Lie algebra |
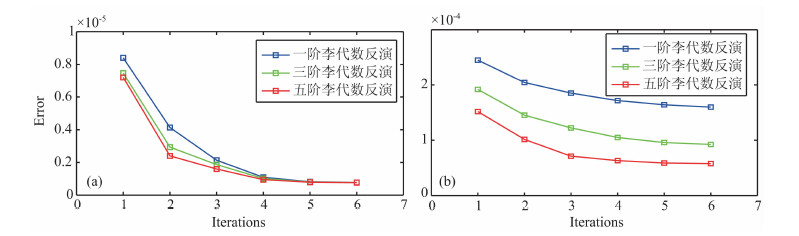
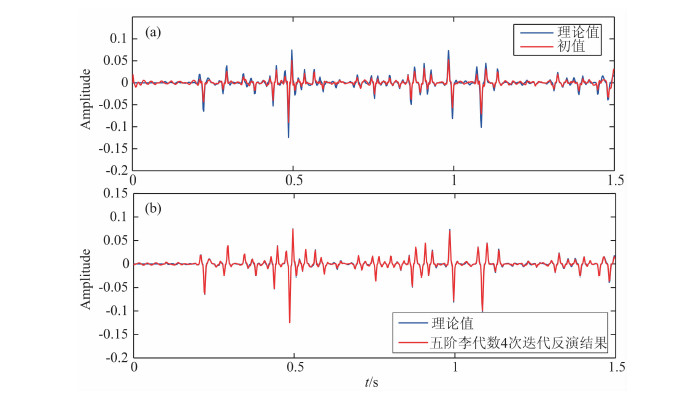
图 4a和4b分别是图 2a和2b所示的反射系数序列的预测算子反演的迭代误差曲线比较,蓝线、绿线、红线分别为一阶、三阶、五阶李代数反演迭代误差曲线.可以看出,在反射系数较小的情况下,一阶李代数反演(即O′Doherty-Anstey公式)即可获得较高的反演精度.而当反射系数较大的情况,五阶李代数反演精度要高于低阶李代数,一般情况下,迭代3次即可停止.图 5a是采用公式(23)(24)得到的反演初值(红线),图 5b为五阶李代数反演迭代4次的结果(红线),和理论值比较可以看出两者基本重合.
|
图 4 不同阶李代数反演迭代误差曲线比较 (a)图 2a反射系数反演误差曲线;(b)图 2b反射系数反演误差曲线. Fig. 4 Error curves of different order Lie algebra inversion (a) Error curves for coefficient series in Fig. 2a; (b) Error curves for coefficient series in Fig. 2b. |
|
图 5 图 2b中反射系数序列李代数反演的初值和结果 (a)迭代反演初值与理论值比较;(b)迭代反演结果与理论值比较. Fig. 5 Initial value and the result of the fifth order Lie algebra inversion to the coefficient series in Fig. 2b (a) Comparison between the initial value and the theoretical value; (b) Comparison between the inversion result and the theoretical value. |
图 6是根据某地实际情况给出的薄层地质模型,最小速度为2050m/s,最大速度为4000m/s,反射系数最大值为0.153;采用12阶有限差分法进行正演模拟,共600炮,横向采样间隔为5 m,纵向采样为0.002s,地震记录为4.5s,最大炮检距为3750m.图 7是对单炮记录消除多重散射流程.首先对单炮记录(图 7a)进行τ-p变换(图 7b),然后采用谱分解算法对每个p道求取预测算子序列(图 7c),然后采用五阶李代数对预测算子序列反演求取有效反射波场(图 7d),最后反演得到的τ-p域反射波场,进行τ-p反变换得到消除多重散射后的炮集记录.

|
图 6 速度模型 Fig. 6 Velocity model |

|
图 7 炮集数据薄层多重散射消除 (a)单炮记录;(b)τ-p变换;(c)预测算子;(d)消除多重散射后的τ-p域地震记录;(e)消除多重散射后的单炮记录. Fig. 7 Multiple scattering elimination for shot gather (a) Shot gather; (b) τ-p transformation; (c) Prediction operator; (d) Seismic record in τ-p domain after multiple scattering elimination; (e) Shot gather after multiple scattering elimination. |
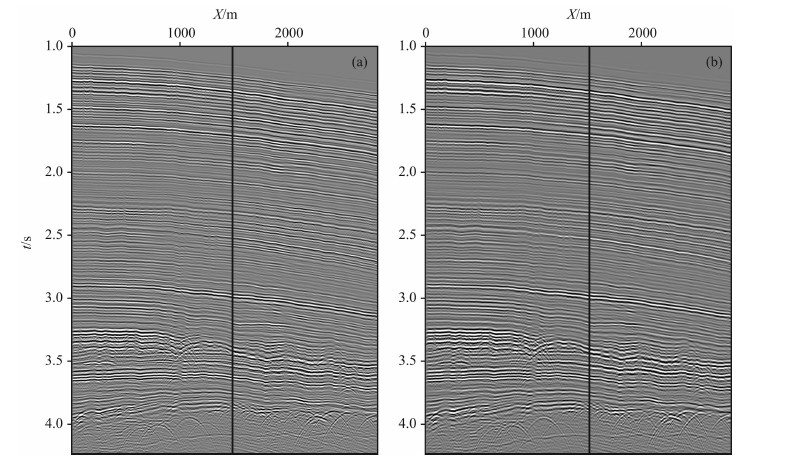
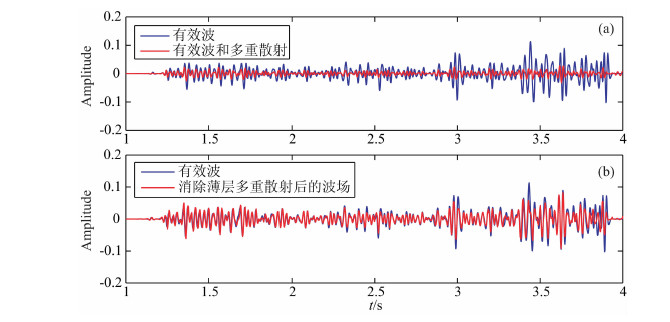
图 8a为原始零偏移距剖面,图 8b为消除多重散射后零偏移距剖面.对比图 8中红线标志的单道记录(图 9)可知,采用基于李代数反演算法消除薄层多重散射能有效地恢复有效波的振幅和校正有效波的相位,为下一步AVO反演等提供更为可信的地震数据.
|
图 8 最小偏移距剖面 (a)多重散射消除前;(b)多重散射消除后. Fig. 8 Zero offset profile (a) Before attenuation of multiple scattering; (b) After attenuation of multiple scattering. |
|
图 9 单道效果对比 (a)多重散射消除前;(b)多重散射消除后. Fig. 9 Single trace (a) Before attenuation of multiple scattering; (b) After attenuation of multiple scattering. |
此外,基于李代数积分的预测算子迭代反演由于在频率域进行,具有快速的优势.以上述模型为例,在2.0G主频,3.25G内存的单机上,单炮一阶李代数反演迭代4次,用时仅需41.3s,单炮五阶李代数反演迭代4次,用时仅需53.6s.
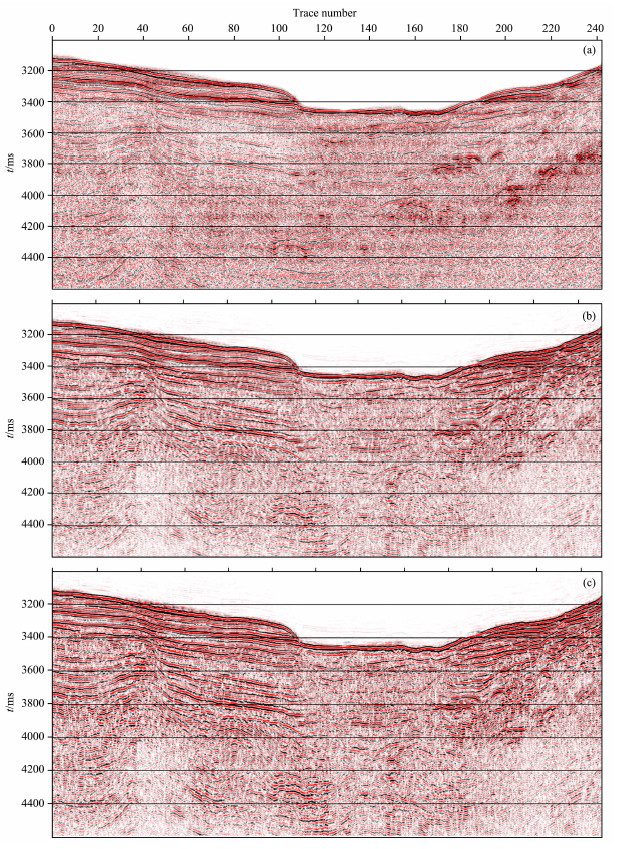
4 实际地震数据处理效果图 10a为某实际地震数据偏移距剖面,薄层多重散射严重影响了中深层的有效信号.图 10b、10c分别为一阶、五阶李代数消除效果,消除多重散射后,中深层信号振幅得到补偿,且薄层多重散射得到有效的压制.五阶李代数和一阶李代数反演效果相比总体差别不大,主要在局部有差别.
|
图 10 实际地震资料的多重散射消除效果 (a)偏移距剖面;(b),(c)一阶和五阶李代数反演多重散射消除效果剖面. Fig. 10 The inversion results for practical application (a) Common offset profile; (b), c) Common offset profiles after eliminating multiple scattering by first order and fifth order Lie algebra integral respectively. |
(1)本文基于李代数积分给出了O′Doherty-Anstey公式的高阶表达形式,当反射系数较大时,高阶O′Doherty-Anstey公式求取的透射波频谱更准确.
(2)基于李代数积分的O′Doherty-Anstey公式的高阶表示,本文提出了李代数反演算法消除地震记录中薄层多重散射的影响.在反射系数较小的情况下一阶李代数反演即可;如果反射系数较大时,需采用高阶李代数反演,一般迭代3~4次即可反演出去除多重散射后的有效波场.同时,频率域运算保证了该算法的高效性,实际运算中,可采用并行算法进行大规模地震数据处理.
致谢衷心感谢两位外审专家提出的合理的意见以及细致的修改工作.同时感谢刘红伟提供了薄层速度模型以及正演数据.
| [1] | Claerbout J F. Fundamentals of Geophysical Data Processing. England: Blackwell Scientific Publications, 1985 : 1 -266. |
| [2] | Liu Y B, Schmitt D S. The transition between the scale domains of ray and effective medium theory and anisotropy: Numerical models. Pure and Applied Geophysics , 2006, 162(7): 1-23. |
| [3] | O'Doherty R F, Anstey N A. Reflections on amplitudes. Geophys. Prospect. , 1971, 19(3): 430-458. DOI:10.1111/gpr.1971.19.issue-3 |
| [4] | Resnick J R, Lerche I, Shuey R T. Reflection, transmission, and the generalized primary wave. Geophys. J. R. Astr. Soc. , 1986, 87(2): 349-377. DOI:10.1111/j.1365-246X.1986.tb06628.x |
| [5] | Shapiro S A, Zien H. The O'Doherty-Anstey formula and localization of seismic waves. Geophysics , 1993, 58(5): 736-740. DOI:10.1190/1.1443458 |
| [6] | Matthew M H, van Kasper W, Snieder R. Radiative transfer in layered media and its connection to the O'Doherty-Anstey formula. Geophysics , 2005, 70(1): T1-T11. DOI:10.1190/1.1852788 |
| [7] | 刘洪, 何利, 刘国峰等.地层滤波公式的李代数积分证明和推广.//中国地质与地球物理研究进展--庆贺刘光鼎院士80华诞.北京:科学出版社, 2008: 412-422. Liu H, He L, Liu G F. Derivation and generalization of the stratigraphic filtering formula via Lie algebraic intergral.//Progress of Geology and Geophyscis in China for 80th Birthday of Academician Liu Guangding (in Chinese). Beijing: Science Press, 2008: 412-422. |
| [8] | Wang Y H. Q analysis on reflection seismic data. Geophysical Research Letters , 2004, 31(17): L17606. |
| [9] | Wang Y H. Inverse Q-filter for seismic resolution enhancement. Geophyscis , 2006, 71(3): V51-V60. DOI:10.1190/1.2192912 |
| [10] | Iserles A, Munthe-Kaas H, Nfrstt S, et al. Lie-group Methods. Cambridge: Cambridge University Press, 2000 . |
| [11] | 李世雄. Lie群与Lie代数简介.北京:中国科学院地质与地球物理研究所, 2005. Li S X. Lie Group and Lie Algebra Integral (in Chinese). Beijing: Institute of Geology and Geophysics, Chinese Academy of Sciences, 2005. http://www.oalib.com/references/18988363 |
| [12] | 张廉萍, 刘洪. 适于Kirchhoff叠前深度偏移的地震走时李代数积分算法. 地球物理学报 , 2010, 53(8): 1893–1901. Zhang L P, Liu H. Lie algebra integral algorithm of travel-time calculation for pre-stack Kirchhoff depth migration. Chinese J. Geophys. (in Chinese) , 2010, 53(8): 1893-1901. |
| [13] | 张廉萍, 刘洪, 李幼铭. 单程波李代数深度积分的精度分析和算法改进. 地球物理学报 , 2010, 53(11): 2739–2746. Zhang L P, Liu H, Li Y M. The precision analysis and algorithm improvement in Lie algebra depth integral of one-way seismic wave. Chinese J. Geophys. (in Chinese) , 2010, 53(11): 2739-2746. |
| [14] | 刘洪, 袁江华, 陈景波, 等. 大步长波场深度延拓的理论. 地球物理学报 , 2006, 49(6): 1779–1793. Liu H, Yuan J H, Chen J B, et al. Theory of large-step wavefield depth extrapolation. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1779-1793. |
| [15] | 刘洪, 刘国峰, 李博, 等. 基于横向导数的走时计算方法及其在叠前时间偏移中的应用. 石油物探 , 2009, 48(1): 3–10. Liu H, Liu G F, Li B, et al. The travel time calculation method via lateral derivative of velocity and its application in pre-stack time migration. Geophysical Prospecting for Prtroleum (in Chinese) , 2009, 48(1): 3-10. |
| [16] | 齐民友, 徐超江, 王维克. 现代偏微分方程引论. 武汉: 武汉大学出版社, 2005 . Qi M Y, Xu C J, Wang W K. Introduction to the Partial Differential Equations (in Chinese). Wuhan: Wuhan University Press, 2005 . |
| [17] | Aki K, Richards P G. Quantitative Seismology: Theory and Methods. San Francisco: W H Freeman and Co., 1980 : 932 . |
| [18] | 田畴. 李群及其在微分方程中的应用. 北京: 科学出版社, 2003 . Tian C. Liu Group and Its Application in the Differential Equations (in Chinese). Beijing: Science Press, 2003 . |
| [19] | 秦孟兆, 陈景波. Maslov渐近理论与辛几何算法. 地球物理学报 , 2000, 43(4): 522–533. Qin M Z, Chen J B. Maslov asymptotic theory and symplectic algorithm. Chinese J. Geophys. (in Chinese) , 2000, 43(4): 522-533. DOI:10.1002/(ISSN)2326-0440 |
| [20] | 刘洪, 袁江华, 勾永峰, 等. 地震逆散射波场和算子的谱分解. 地球物理学报 , 2007, 50(1): 240–247. Liu H, Yuan J H, Gou Y F, et al. Spectral factorization of wavefield and operator in seismic inverse scattering. Chinese J. Geophys. (in Chinese) , 2007, 50(1): 240-247. |
 2013, Vol. 56
2013, Vol. 56


