2. 海洋石油勘探国家工程实验室, 西安 710049;
3. 中国石油长庆油田分公司勘探开发研究院, 西安 710021;
4. 低渗透油气田勘探开发国家工程实验室, 西安 710018
2. National Engineering Laboratory for Offshore Oil Exploration, Xi'an 710049, China;
3. Research Institute of E & D, Changqing Oil-Field Company of CNPC, Xi'an 710021, China;
4. National Engineering Laboratory for Exploration of Low Permeability Oil-Gas Field, Xi'an 710018, China
地层是黏弹性介质,地震波在地下传播过程中,由于介质的吸收效应,致使产生波的衰减和频散.Q值[1-2]是度量介质衰减特性的重要参数,也是指示地层含油气性的重要属性之一.由地震资料估计的地层衰减(Q值)不仅可用于岩性及含流体分析、储层识别和烃类检测等,也可用于对地震资料进行吸收补偿,提高地震资料分辨率等[3-4].
目前常用的估计Q值的地震资料有垂直地震剖面(VSP)资料、井间资料、叠后反射地震资料、叠前反射地震资料等.VSP资料信噪比高但成像范围小;井间地震资料能提供高精度的井间储层信息但其费用昂贵;地面地震资料在横向上可在很大范围内追踪地层厚度和岩性变化,但地面地震资料的纵向分辨率相对较低,且是远离地层界面的间接观测.叠后反射地震资料的信噪比高,但是经过动校正(NMO)拉伸却损坏了频率信息[5];叠前反射地震资料虽然信噪比较低,但是比叠后反射地震资料有更加精确的地层信息及丰富的振幅和走时信息,频率无损坏,一些细微的地层特征在叠后地震资料上是看不到的,尤其是存在薄互层时,叠后地震资料很难区分散射与吸收.鉴于叠前资料丰富的振幅和频率信息,我们有必要研究基于叠前反射地震资料的介质品质因子估计方法.
已有许多学者对叠前地震资料的衰减估计技术进行了研究.王小杰和吴国忱[6]提出了基于叠前资料利用时频谱分解技术估算地层吸收参数的方法,他们基于地震子波为一般零相位子波的假设,用质心频率偏移法、斜率法、谱比法实现了衰减估计,然而没有讨论射线几何路径不同对吸收参数的影响,即具有不同入射角的射线穿过多层介质时,如何拾取层间走时的问题.他们采用频率域方法估计Q值,这些方法大多需加时窗截取地震记录并用Fourier变换计算频谱,而在实际问题中恰当地选择窗函数的类型及长度是比较困难的.Zhang和Ulrych[7-8]提出了基于叠前CMP资料且用PFS法(峰值频率移动法)估计Q值的方法,即结合先验的层位信息拾取该层位对应的地震道的非零偏移距处的峰值频率,然后用PFVO(峰值频率随偏移距变化关系)方法外推出该同相轴零偏移距处的峰值频率,进而用PFS法计算出Q曲线.该方法把叠前Q值提取问题转换为类似叠后Q值提取问题,解决了直接利用叠前资料时走时难提取的问题.Zhang提出的PFS法假设震源子波是零相位的Ricker子波,当震源子波满足假设条件时估计的Q值精度较高,然而在实际资料中,震源子波通常不是零相位的,导致该方法估计的Q值误差较大[9];另外Zhang的方法的实现步骤中,用包络峰值处瞬时频率EPIF代替峰值频率PF,二者的定义不同,求取方法不同,稳定性不同,可能会导致误差.高静怀和杨森林等[10-11]提出用WEPIF(子波包络峰值处瞬时频率)方法估计Q值,该方法利用子波包络峰值处瞬时频率与衰减之间的关系来估计Q值,有更高的纵向分辨率,能避免加时窗问题,抗噪性好而且更易于实现.基于上述讨论,本文发展WEPIF方法,研究适合一般地震子波的叠前CMP资料衰减估计技术.
本文第二部分阐述了该方法的原理,详细推导了EPIF与偏移距满足的关系,并讨论了含倾斜界面地震资料的Q值估计方法;第三部分给出了具体的实现方法,包括层位的拾取方法、瞬时频率的计算方法、子波参数的估计方法、计算步骤等;第四部分给出数值仿真及实际资料的估计结果.
2 原理 2.1 EPIF与偏移距的关系(EPIFVO)处理叠前资料的一个难点是波在各层间传播的走时难提取.图 1是水平层状介质中波传播示意图. 图 1a中,检波器R1处接收到的波传播走时与入射角θ1有关,检波器R2处接收到的波的走时与入射角θ1及透射角θ2有关,以此类推,多层介质的波传播走时与各层入射角及透射角有关,即与介质的速度、密度等有关,但实际中获取精确的角度信息及介质参数比较困难.而零偏移距道的波是垂直入射垂直反射的,如图 1b所示,各层的入射角和透射角都已知,故其走时可以通过测井曲线或叠后资料等途径得到,因此我们试图寻找不同偏移距处的EPIF与偏移距或走时的关系,以期利用该关系外推出零偏移距道的EPIF,进而利用零偏移距道资料求取Q值,这样就可以避免求取不同偏移距处的层间走时.
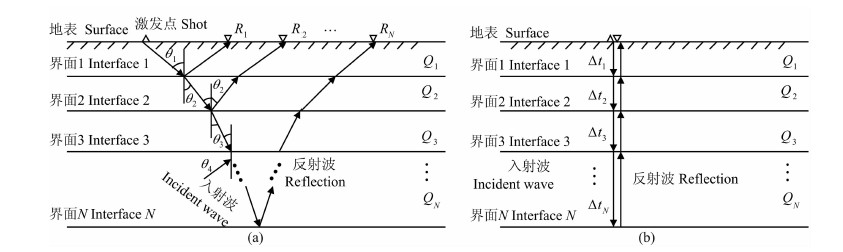
|
图 1 (a)最短时间路径;(b)零偏移道的波传播示意图 Fig. 1 (a) Minimal time propagation; (b) Wave propagation of the zero-offset trace |
下面推导EPIE与走时的关系.
2.1.1 单层介质的情况本小节介绍单层介质时EPIF与走时的关系.假设震源子波可以用如下具有4个参数的常相位子波近似[11-12]:
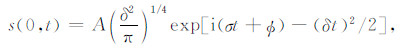
|
(1) |
其中,σ为调制角频率,δ为能量衰减因子,A和ϕ分别为振幅和相位.
对(1)式两边做Fourier变换得:
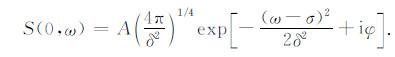
|
(2) |
在水平层状黏弹介质中,假设Q值与频率无关,只考虑单程波传播[10, 13],则由衰减引起的振幅变化的表达式为[14]:
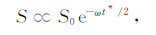
|
(3) |
其中,
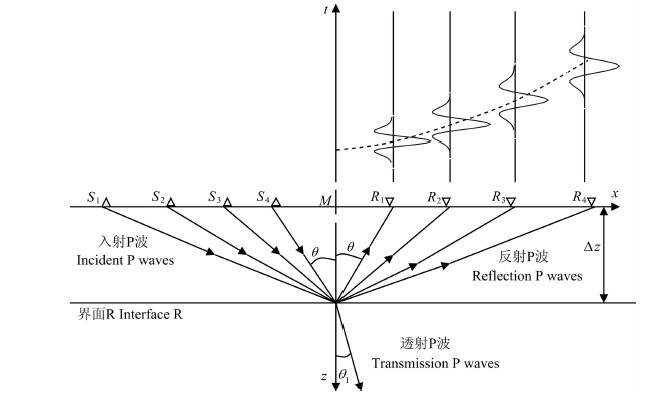
地震子波以入射角θ传播到厚度为Δz的界面又反射回地面(如图 2所示)后,将(2)式代入(3)式可得子波的反射波频域表达式[15],即
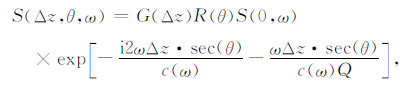
|
(4) |
其中ω为角频率,Δz为地层厚度,G(Δz)和R(θ)分别为不依赖于频率和吸收的因子(如几何扩散等)及界面反射系数,c(ω)为相速度,S(0,ω)为初始时刻的震源子波频域表达式,S(Δz,θ,ω)为检波器接收到的反射波的频域表达式.
|
图 2 入射P波、反射P波、透射P波的关系及CMP模型示意图 Fig. 2 Relationship of incident P wave, reflection P wave and transmission P wave and sketch maps of CMP model |
Barnes指出,常相位子波的包络峰值瞬时频率(EPIF)等于子波振幅谱对Fourier频率加权的平均频率[13, 16],即
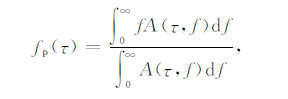
|
(5) |
其中,A(τ,f)为子波的傅里叶振幅谱,即Fourier谱的模.
将式(2)的模代入式(5)得到零时刻地震子波的EPIF:
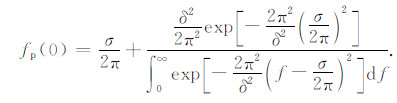
|
(6) |
若忽略速度频散,即c(ω)=c,则将(2)式代入(4)式可得子波传播时间τ后的振幅谱:
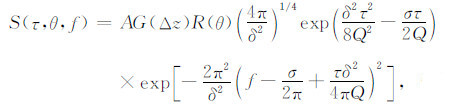
|
(7) |
其中,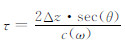
将(7)式代入(5)式得到传播时间τ之后子波的EPIF如下:
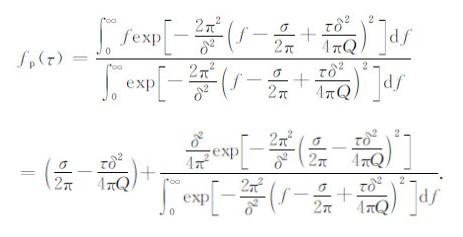
|
(8) |
由(8)式可以看出,影响子波振幅谱的振幅因子A、不依赖于频率的因子G(Δz)及反射系数R(θ),在求取包络峰值瞬时频率时由于比值关系而相互抵消,因此在层状均匀黏弹介质中,不考虑多次波的情况下,利用EPIF可以消除界面反射系数、振幅等因素的影响.
类似文献[11]中的推导过程,将式(8)经过一系列的展开、变量替换及舍去高阶项后得到:
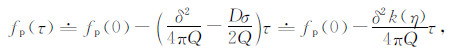
|
(9) |
其中,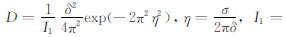
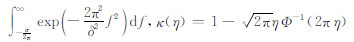
由(9)式可见,传播一定时间后子波的EPIF与走时近似为线性关系,其截距是初始时刻子波的EPIF,斜率与Q有关.
2.1.2 多层介质的情况2.1.1节介绍的是单层介质的情形,本节将其推广到多层介质的情况.假设介质有N个反射界面,检波器得到的经第N个界面反射的反射波为[7]:
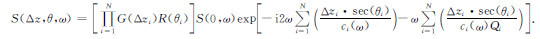
|
(10) |
若忽略速度频散,令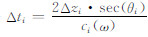
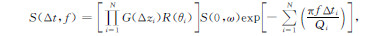
|
(11) |
(11)式代入(5)式得到EPIF的表达式后,将其展开、变量替换及舍去高阶项后得到:
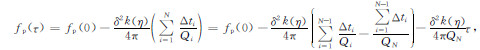
|
(12) |
其中Δti是反射波在第i层的双程走时,τ=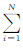
从(12)式可以看出,N层介质时子波的EPIF与走时仍然满足线性关系,但它的截距除了与零时刻震源子波的EPIF有关外,还与各层介质的走时及品质因子有关,而走时Δti因射线入射角不同而不同,故其截距不是常数,因此不能用此公式直接求衰减.
地震波传播时真正遵循的是“沿最小时间路径传播”原理(费马原理),如图 3a所示.在小偏移距小排列的情况下,将多层介质的反射波时距曲线近似地看成双曲线,在一定精度要求下是可以的[17].讨论层状介质问题的基本思路是:如图 3a所示的水平层状介质,我们可以把R2界面以上的介质设法用等效均匀介质来代替,并令这种假想的均匀介质的波速度及品质因子取某个等效值,使得R2界面以上的介质简化为均匀介质,即变成单层模型[17],同样可以把RN界面以上的N层介质用具有某个等效品质因子的均匀介质来代替,如图 3b所示.
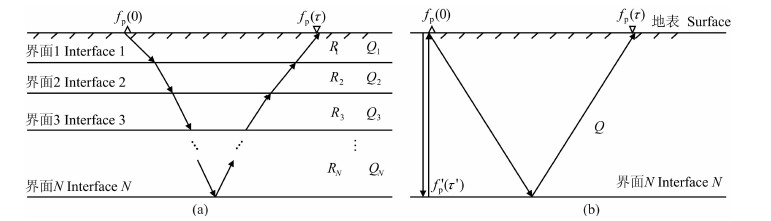
|
图 3 多层介质(a)简化为单层介质(b) Fig. 3 Multilayer medium (a) reduces to one-layer medium (b) |
令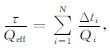
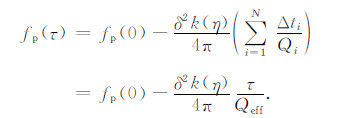
|
(13) |
(13)式与(9)式形式相同,不同点是(13)式中的Q为等效Q值,而(9)式中的Q为层间Q值.
下面分析(13)式的意义及作用.(13)式表示的是地表上震源与接收点的EPIF与走时的关系.沿每个同相轴拾取不同偏移距处的EPIF和走时并进行线性回归,计算斜率和截距,进而外推出零偏道子波的EPIF,这就是EPIFVO的定义.由(13)式看出,斜率应该是负的,若拟合出的斜率为正,则认为此处频率的变化不是由衰减引起的,可能是由薄互层导致的同相轴调谐,故需先处理异常值.关于异常值处理的方法将在4.2节介绍.
前面讨论单层及多层介质中EPIF与走时满足的关系时,波是从零时刻开始传播的,为了求取Q值方便,下面将其推广到以任意时刻为起始点时的情况.
设震源子波的振幅谱为S(0,f),那么对于某一同相轴,零偏移距处(M点)接收到的子波振幅谱为:
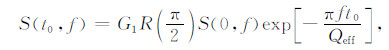
|
(14) |
而偏移距x处(R点)接收到的子波振幅谱为:
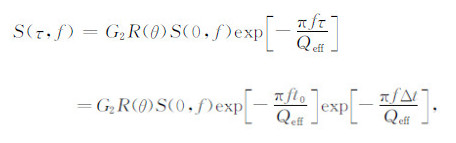
|
(15) |
其中,τ与t0满足τ=t0+Δt.
将(14)式代入(15)式,可得:
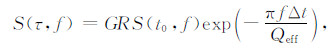
|
(16) |
其中G=G2/G1,R=R(θ)/R(π/2).
将(16)式代入(5)式,经过与式(9)类似的推导,得到初始时刻为t0时τ时刻子波的EPIF为:
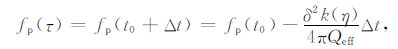
|
(17) |
其中,fp(t0)为中点处接收到的子波的包络峰值瞬时频率.由式(17)可知,若线性拟合时采用正常时差Δt(即垂直时差),则拟合出的直线的截距为该同相轴零偏移距处的EPIF.
2.1.3 含倾斜反射界面时的情况2.1.2节讨论的是水平层状介质的情况,本节讨论含倾斜反射层的情况.界面倾斜时,中心点在界面的投影与真正的反射点有偏移.单个倾斜层的情况下(如图 4所示),假设每个炮点的震源子波相同,从叠前CMP资料的时距曲线上拾取接收信号的走时τ,若先验已知中心点M处的自激自收走时t0(射线垂直于界面入射),可以证明,不管是沿上倾方向还是下倾方向,中心点M处的走时t0是最小的.
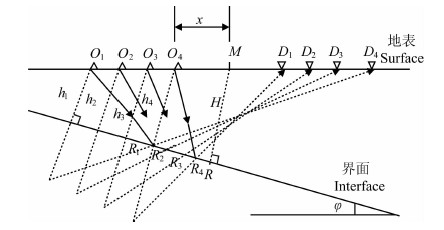
|
图 4 单个倾斜界面示意图 Fig. 4 Single dip reflector diagram |
证明如下:
设H为M点处界面的法线深度,x为炮检距,根据几何关系且应用余弦定理,则偏移距x/2处射线的路程平方为:
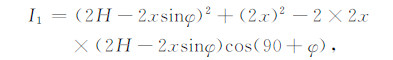
|
中心点M处的垂直路程平方为I2=(2H)2,路径差I=I1-I2=4x2(1-sin2 φ) > 0,速度为常数.这样就可以用式(17)求出单个倾斜层零偏移距处的EPIF.
由于速度均匀,因此对水平层状介质的EPIFVO分析同样适用于单个倾斜层的情况.根据(9)式及(17)式可以用线性回归的方法求出零偏移距处的EPIF,若线性回归时所用的时间为接收信号的走时τ,则拟合得到的截距为震源子波的EPIFfp(0),若线性回归时所用的时间为正常时差Δt=τ-t0,则拟合得到的截距为中心点M在界面上的投影点R处的EPIFfp(t0),用2.2节介绍的Q值计算公式可求得Q曲线.
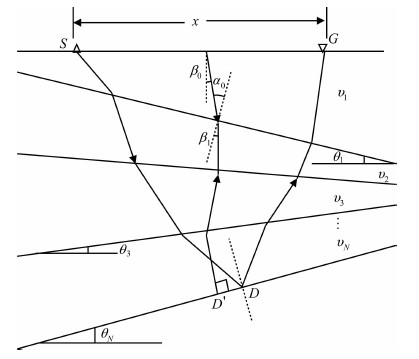
多个倾斜层的情况下,每一层有任意倾斜角,如图 5所示.CMP数据的中心点M在目标反射界面上垂直入射到D′,实际路径的反射点为D.Hubral和Krey [18]提出射线沿SDG的走时公式为:
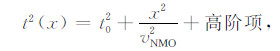
|
(18) |
|
图 5 多个倾斜界面示意图 Fig. 5 Multi-layer dip reflectors diagram |
其中,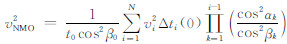
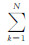
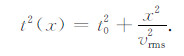
|
(19) |
这种双曲线形式的时距曲线是我们所熟知的,水平层状介质及单个倾斜层模型的时距曲线都是双曲线,因此小倾斜角小排列时,多个倾斜层的介质可以简化为单个倾斜层模型,用EPIFVO方法外推出零偏移距处的EPIF后,由2.2.1节介绍的逐层递推法求出Q值.
2.2 两种求取Q值的方式至此我们已经求出了零偏移距道处各同相轴的EPIF.零偏道中地震波是垂直入射、垂直反射的.下面推导利用零偏移距道的EPIF计算Q值的公式.
2.2.1 逐层递推方式如图 6a所示,在第N个同相轴的零偏移距处,子波的走时为τ,拾取的EPIF为fp(τ),震源子波的EPIF为fp(0),则由式(13)第一个等号左右两边的多项式可得:
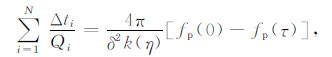
|
(20) |
其中,Δfp=fp(0)-fp(τ)为子波的EPIF之差,Δti为零偏移距道第i层的垂直双程走时,Qi为各层间Q值.
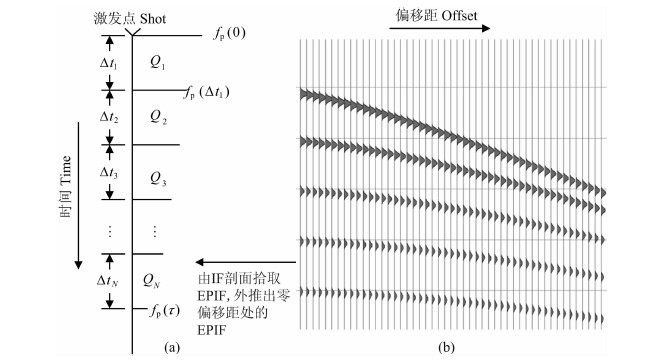
|
图 6 EPIFVO示意图 (a)零偏EPIF;(b)CMP道集的瞬时频率IF剖面. Fig. 6 EPIFVO diagram (a) EPIF at zero-offset; (b) IF section of CMP. |
将(20)式左边展开,得
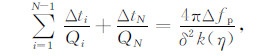
|
(21) |
移项后得
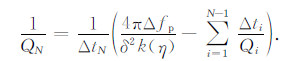
|
(22) |
(22)式为计算各层衰减的逐层递推公式,其中Δfp为震源子波的EPIF与检波器接收到的子波的EPIF之差,第N层的衰减估计精度依赖于其上各层的衰减估计精度,因此有误差累积效应.
2.2.2 相邻两层直接求取方式将(13)式做如下变形:
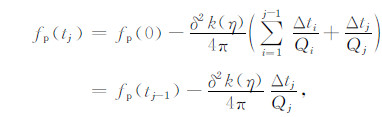
|
(23) |
进而可得出层间Q值的另一个计算公式:
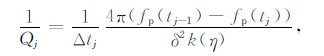
|
(24) |
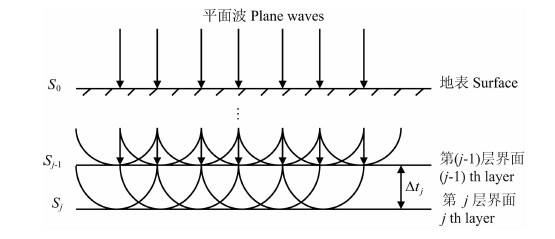
其中下标j表示第j层介质.式(24)的物理意义是:当震源子波传播到第j-1层后,根据惠更斯原理,将该子波波前作为子波源,向各方向继续传播,经过时间Δtj/2后子波到达第j层并反射,在第j-1层接收到反射波,如图 7所示.fp(tj-1)为第j-1层子波源的EPIF,fp(tj)为接收到的反射波的EPIF.利用(24)式就可以求出第j层的层间Q值.这样利用零偏移距道相邻两层之间子波的EPIF变化来估计Q值可以避免误差累积效应.
|
图 7 惠更斯原理示意图 Fig. 7 Huygens principle diagram |
通过以上公式的推导及水平层状介质和倾斜层状介质中EPIFVO方法的讨论可知,实现该方法首先要确定同相轴的位置,计算各非零偏移距道的EPIF,外推求出零偏移距处的EPIF,求取子波参数然后利用WEPIF方法求Q值.本节讨论各步骤的具体实现方法.
3.1 层位信息拾取处理实际资料时,由叠后数据或测井资料拾取到的层位信息与叠前CMP资料的同相轴位置不是完全吻合,因此本文不直接用反射系数序列来引导同相轴位置的拾取,而是利用叠前CMP道集中道与道之间的相关性并结合先验的层位信息来拾取.在叠前CMP道集中,每一道的有效信号与邻近道的有效信号具有相关性,而噪声无相关性,故我们用近偏移距处相邻的几道地震记录来确定同相轴位置.目标函数为:

|
(25a) |
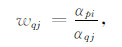
|
(25b) |
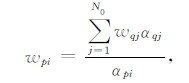
|
(25c) |
其中p为选取的参考道的数目,αp为由近偏移距的几道选出的参考道确定的同相轴位置,wp及wq为相邻道层位位置相关性的权重,αq为除参考道外其余几道提供的同相轴位置,αp、αq、wp、wq同为列向量,下标i、j分别为列向量的元素,N0、N1为向量元素个数.
层位拾取的实现步骤如下:
(1)选取近偏移距中的几道,如选取叠前CMP资料的第1~5道(即p=5),计算这五道的瞬时振幅IA和瞬时频率IF,由IA和IF拾取EPIF[19]及其位置α,我们认为EPIF的位置等效为同相轴的位置,EPIF的位置为一个列向量;
(2)从近偏移距的几道中选取参考道,如选取第一道作为参考,根据式(25b),求参考道的EPIF位置向量的某一元素αpi与某一非参考道的EPIF位置向量每个元素αqj的比值以确定wqj.若wqj达到给定的阈值,则wqj置1,否则置0;求出所有wqj后,根据式(25c)确定wpi;遍历参考道EPIF位置向量的所有元素,最终确定wp;参考道不变,将上述过程遍历其它非参考道,每次将wp累加且将wq清零;
(3)依次从近偏移距的几道中选取其它道作为参考道,重复第2步的操作,并将每次求得的权重wp累加;若某位置wp的值达到给定的阈值,则认为该位置是同相轴位置.该步骤可以避免参考道的某层反射受干扰的情况;
(4)用同样的方法求取由选取的近偏移距地震道确定的参考同相轴位置与先验层位信息提供的同相轴位置的相关系数,确定最终的同相轴位置.
3.2 计算瞬时频率及估计子波参数瞬时频率的计算可以直接采用瞬时频率的定义,即瞬时相位的导数,对于含噪信号,通常采用阻尼瞬时频率以增加计算的稳定性[13, 16],即
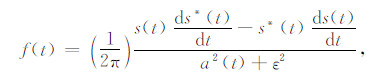
|
(26) |
其中s*(t)是信号s(t)的希尔伯特变换,ds*(t)是s*(t)的导数,a(t)是瞬时振幅.
为了进一步稳定瞬时频率,通常还用地震信号幅度的平方对阻尼瞬时频率加权,即

|
(27) |
其中,W(t′)为信号幅度的平方,L为加权窗的长度.
利用WEPIF法估计Q曲线时,需要知道子波调制频率σ和能量衰减因子δ的值.可用如下公式近似计算[10, 20]:
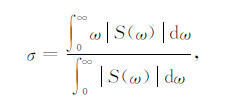
|
(28) |
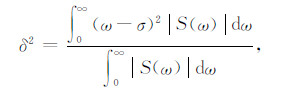
|
(29) |
其中S(ω)为子波s(t)的频谱.
3.3 EPIFVO计算步骤用WEPIF方法[13, 21-23]估计叠前CMP道集的Q值前,先进行预处理,去除不同炮子波的不一致性.EPIFVO的实现步骤如下:
(1)构造一个CMP超道集;
叠前数据信噪比低,因此在每道数据的邻域内选择极少的几道构造一个CMP超道集,对子波特征破坏不大,又可起到压制部分随机噪声的作用.
(2)每道数据用三参数小波做小波变换,在小波域计算瞬时振幅IA和瞬时频率IF;
(3)根据道与道的相关性拾取叠前CMP数据的同相轴,即确定层位信息;
(4)根据层位信息,在反射界面附近拾取各道IA的包络峰值对应的瞬时频率,即包络峰值处瞬时频率EPIF,由于水平层状介质中各同相轴的时距曲线是双曲线,故同相轴位置满足如下约束条件:
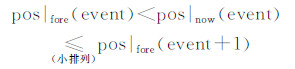
|
其中,pos|now(event)为当前道某同相轴的位置,pos|fore(event)为前一道同一个同相轴的位置,即当前道的同相轴位置必然大于前一道同一同相轴的位置,而有可能小于前一道下一同相轴的位置(小排列时成立,而同相轴有交叉时可能不成立),实际中利用同相轴的梯度信息拾取连续同相轴更准确;
(5)单个同相轴计算,从叠前剖面上拾取波至时间,用不同偏移距处的EPIF和走时差(即正常时差)线性回归计算斜率和截距(截距即零偏移距道的EPIF),并处理异常斜率对应的截距;
(6)用WEPIF法计算Q曲线.
4 算例与分析 4.1 合成叠前CMP资料首先用一个合成的叠前CMP资料来检验文中所提方法的有效性.图 8a为模型的参数和观测系统.正演叠前CMP资料时,震源子波采用主频为50Hz的常相位子波,最小炮检距为10 m,用49个间距为5m的检波器进行接收,共49道,采样率为1ms.叠前CMP资料的正演采用基于Fermat原理的射线追踪法,正演的数据如图 8b所示.合成资料共5个同相轴,各层理论的层间Q值分别为150、200、100、150、250.
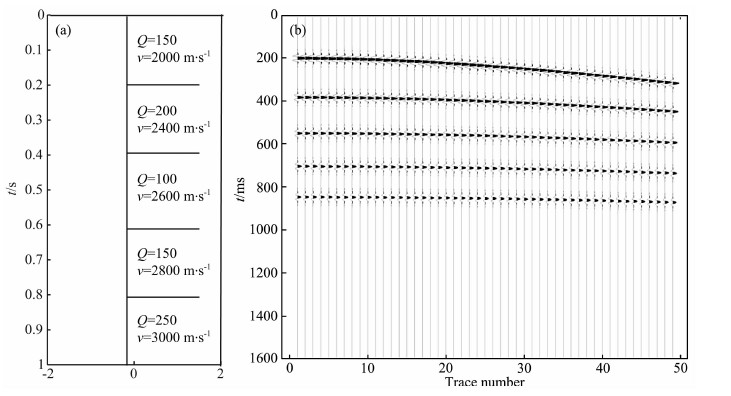
|
图 8 模型的参数和观测系统(a)与正演的叠前CMP资料(b) Fig. 8 The parameters and observation system of the model (a) and the synthetic seismogram (b) |
图 9为5个同相轴的子波EPIF与偏移距的剖面,可以看出其为双曲线;
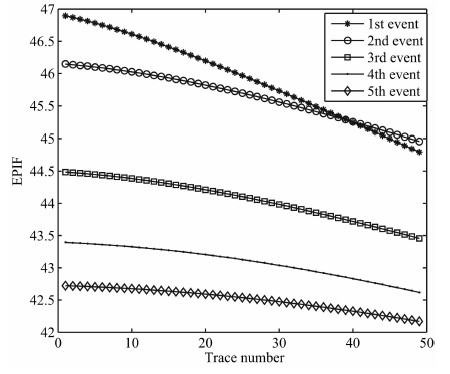
|
图 9 子波EPIF与偏移距的剖面 Fig. 9 The wavelet EPIF section of all events along offsets |
图 10为5个同相轴的子波EPIF与时间的剖面,周围的5个图分别为5个同相轴的EPIF与时间关系的放大图,可以看出5个同相轴都近似满足线性关系,验证了理论的正确性.
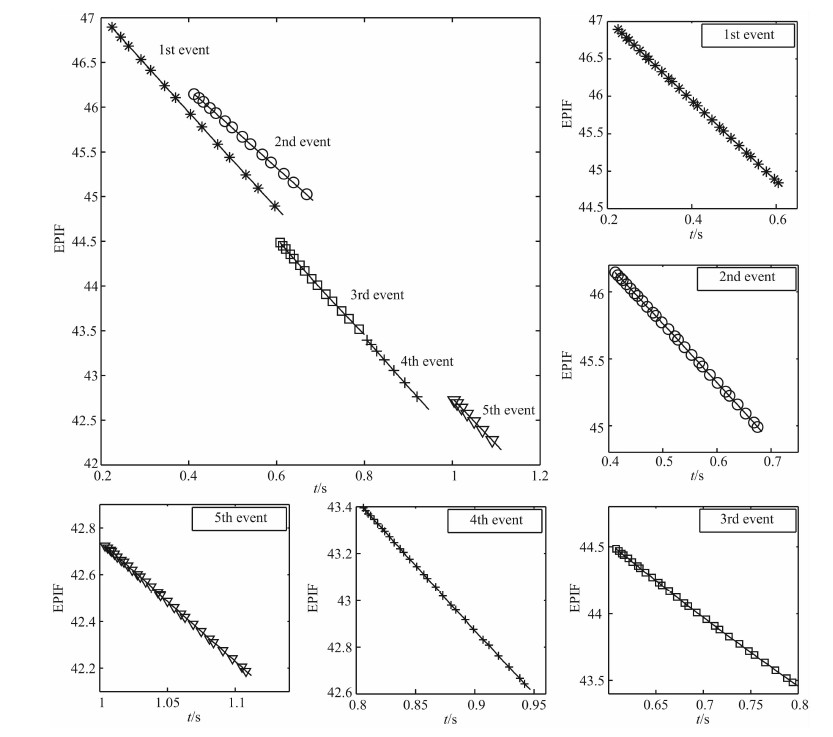
|
图 10 各同相轴的子波EPIF与时间的剖面 Fig. 10 Wavelet EPIF section of all events along time |
本文对比了WEPIF法和Zhang文章中所用的PFS法估计Q值的精度.WEPIF法和PFS法对子波有一定的依赖性[24],WEPIF法对子波的依赖性要小于PFS法.合成记录的子波参数η=0.467.基于形如公式(1)的震源子波推导出PFS法的Q值计算公式为:
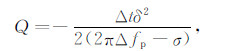
|
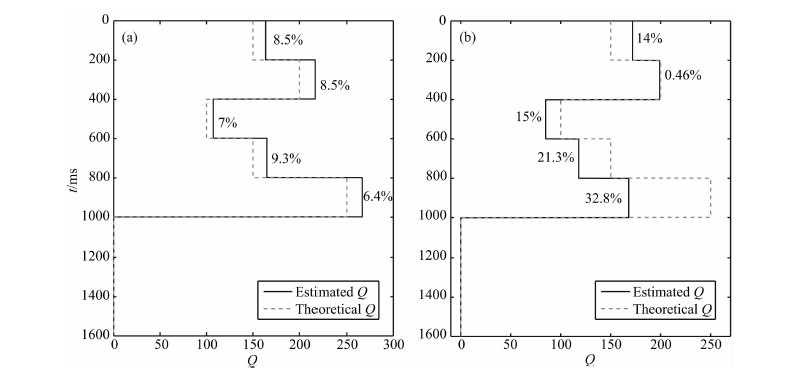
其中Δfp为峰值频率的差,σ,δ为子波参数.图 11a为根据公式(24),利用相邻两层的EPIF,用WEPIF法估计的衰减曲线,其中点线是真实的Q值,实线是估计的Q值,估计的误差均在合理范围内,验证了该方法的有效性;图 11b为PFS法估计的衰减曲线,其中虚线是真值,实线是估计的Q值,从图中可见误差较大.
|
图 11 以相邻两层直接求取方式用WEPIF法估计的衰减曲线(a)和用PFS方法估计的衰减曲线(b) Fig. 11 (a) The estimated Q curve using WEPIF analysis by neighbor layers way and (b) the estimated Q curve using PFS |
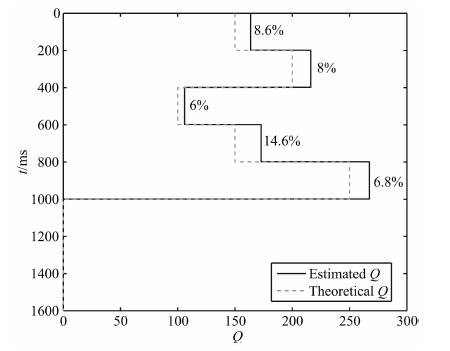
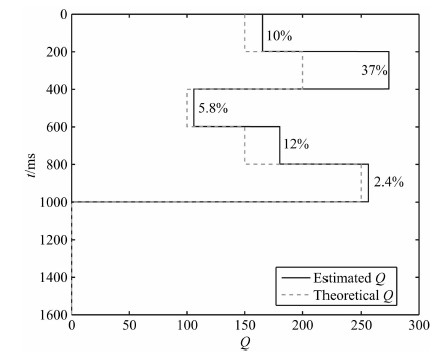
图 12为用逐层递推公式(22)用WEPIF方法估计的衰减曲线,可以看出深层的误差较大,误差累积效应较明显.
|
图 12 以逐层递推的方式用WEPIF法估计的衰减 Fig. 12 The estimated Q curve using WEPIF analysis by the layer-by-layer recursion way |
由式(13)可知,线性回归的斜率为Gf=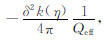
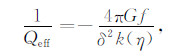
|
(30) |
进而用公式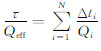
|
图 13 用线性回归得到的斜率估计的衰减 Fig. 13 The estimated Q by the gradient obtained from the linear regression |
由图 13可看出,直接用斜率估计衰减的误差波动较大,估计结果不稳定,原因是线性回归时需要进行人机交互修正部分EPIF值,以图 14a所示的序列为例,如图 14b所示,只上下移动第一个和第三个点,线性回归得到的斜率和截距差距很大.
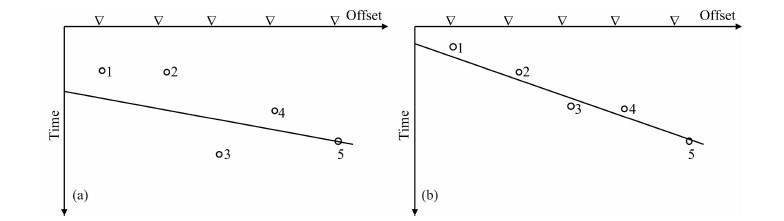
|
图 14 人机交互误差产生示意图 Fig. 14 Error caused by man-computer interacting |
式(30)中Qeff与斜率成正比例关系,故误差较大,且求取层间Q值时有误差累计效应,而式(22)及式(24)中Q与Δfp(EPIF之差)有关,若人机交互采用的准则相同,两个包络峰值瞬时频率(EPIF)相减可以消去部分人机交互带来的主观影响,且可以直接求取层间Q值.
4.2 合成含有薄层调谐效应的CMP数据我们用射线追踪法合成一个含有薄互层的模型,其中第四层为薄互层,最后一层的Q为50,其上各层的Q为500,其余参数与图 8a所示相同.图 15a为反射系数序列模型(本图指示反射系数的时间位置,长短不代表反射系数的数值),图 15b为合成的叠前CMP数据,第四层的上下两个同相轴由于调谐使得分辨率降低,波形干扰使得两个同相轴相互耦合成波形展宽的一个同相轴.
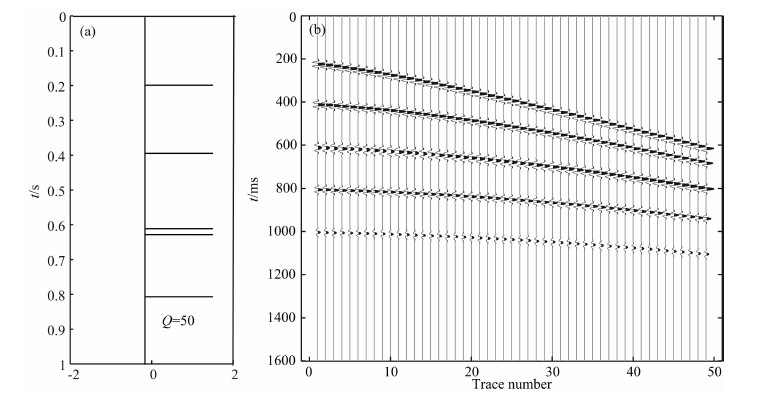
|
图 15 反射系数序列模型(a)和射线追踪法合成的叠前CMP资料(b) Fig. 15 The reflectivity model (a) and the synthetic pre-stack CMP gather using ray tracing method (b) |
5个同相轴线性回归拟合的斜率和截距如表 1所示,第3个同相轴的斜率为正,其余同相轴的斜率为负.2.1节指出,拟合的斜率应该是负的,如果为正,说明频率变化不是由衰减引起的,故需处理异常.表 1的结果验证了理论的正确性.本文处理异常的方法是,若斜率为正,则将对应的截距取其相邻两个截距的平均.
|
|
表 1 拟合的5个同相轴的斜率和截距 Table 1 The intercept and gradient fitted linearly |
图 16a为未处理异常时估计的衰减曲线,误差较大,图 16b为处理异常后估计的衰减曲线,其误差在合理范围内.

|
图 16 未处理异常的衰减曲线(a)和处理异常后估计的衰减曲线(b) Fig. 16 (a) The estimated Q curve before abnormal processing and (b) the estimated Q curve after abnormal processing |
为了分析误差来源,我们设计了一个水平层状单层模型,如图 17所示.
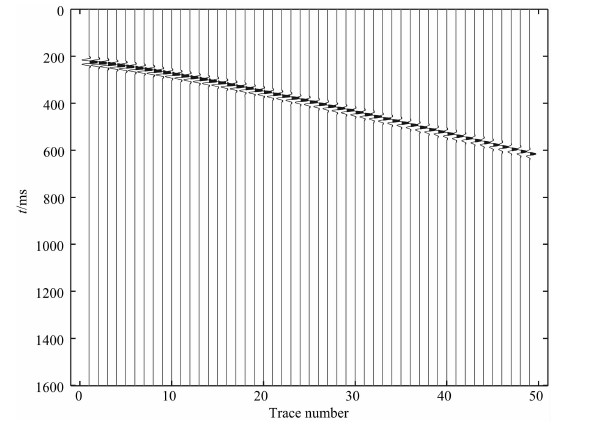
|
图 17 单层水平层状介质合成记录(用于误差测试) Fig. 17 Single horizontal layer-medium synthetic pre-stack CMP gather |
模型中理论Q值是75,若用估计的子波参数计算Q值,结果是79.58971,误差为6.11%,若采用理论的子波参数及精确的反射层位置计算Q值,结果是80.473920,误差是7.29%,此处将Q值计算公式重复如下:
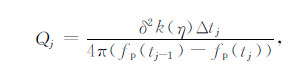
|
δ是能量衰减因子,其理论值是107.0663,估计值是107.1709,k(η)是子波参数的函数,其理论值为0.9841,估计值为0.9763,子波理论主频为50 Hz,估计的主频是48.14Hz.可见子波参数对估计精度的影响较小,而线性回归得到的EPIF误差较大,故其对衰减估计精度的影响较大.
4.3 合成单个倾斜层状介质的叠前CMP资料我们用射线追踪法合成单个倾斜界面的叠前CMP资料,如图 18所示.
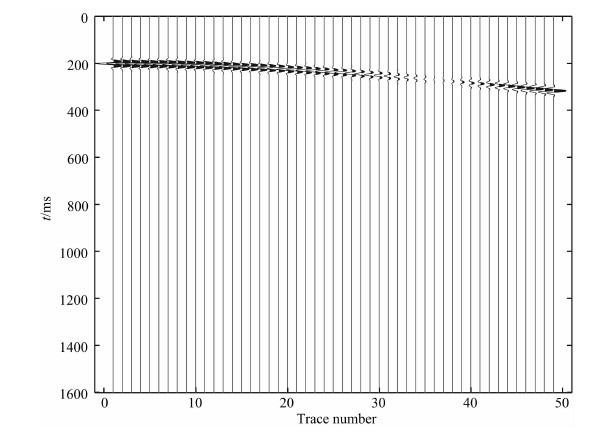
|
图 18 单个倾斜层状介质合成记录 Fig. 18 Single dip layer-medium synthetic pre-stack CMP gather |
倾斜角度为3°,理论Q值为75,估计的衰减值为79.7872,误差在合理的范围内,如图 19所示.
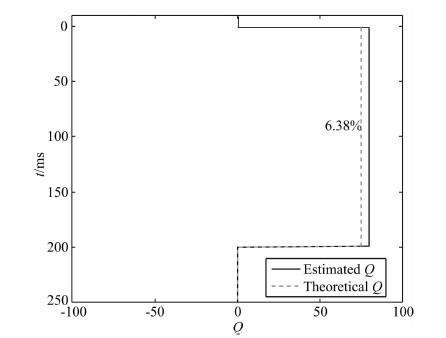
|
图 19 单个倾斜层叠前CMP合成资料的衰减估计曲线 Fig. 19 The eatimated Q-curve from single dip layer-medium synthetic pre-stack CMP gather |
我们将该方法用于长庆油田的某叠前CMP资料.图 20a为该资料的叠后数据,图 20b为叠前CMP资料,截取其中的49道,其目的层大致在1950~2150 ms之间,2090~2130 ms之间是煤层,其附近可能有油气.
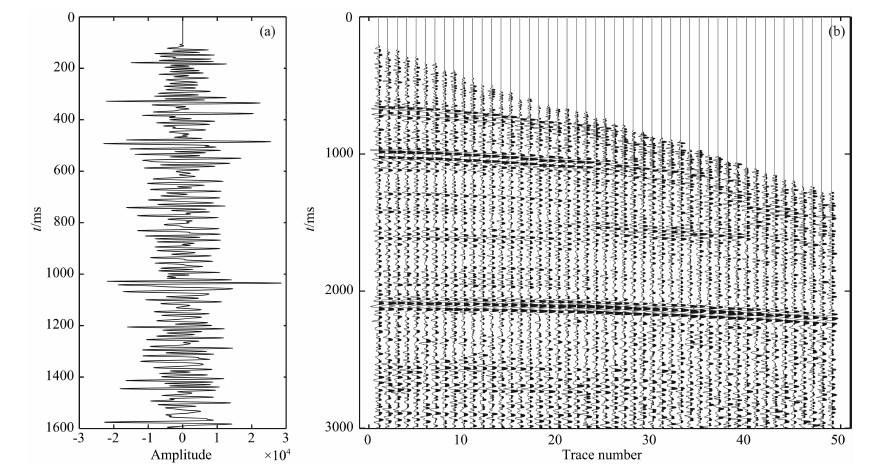
|
图 20 实际资料的叠后数据(a)和实际叠前CMP数据(b) Fig. 20 The post-stack data of the real dataset (a) and real pre-stack CMP record (b) |
图 21a为实际资料的瞬时振幅剖面,图 21b为实际资料的瞬时频率剖面.
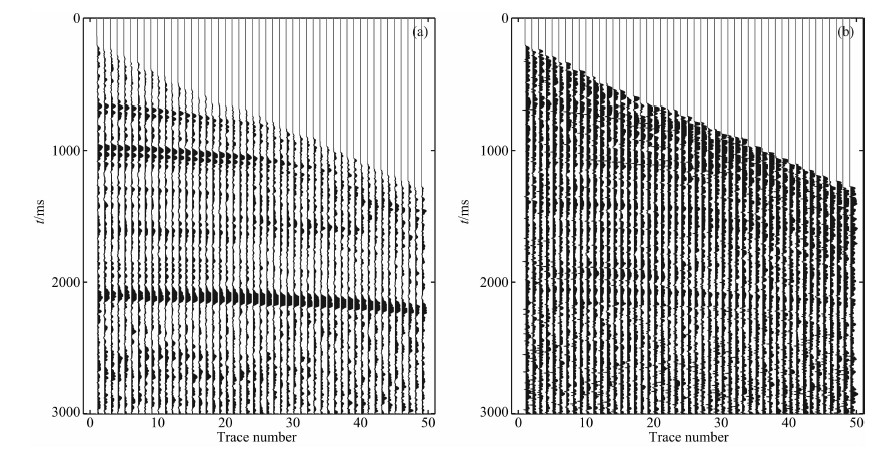
|
图 21 实际叠前CMP资料的瞬时振幅剖面(a)和瞬时频率剖面(b) Fig. 21 (a) Instantaneous amplitude section and (b) instantaneous frequency section of real pre-stack CMP data |
图 22a为叠前CMP资料估计的衰减曲线,图 22b为该叠前数据叠加后形成的叠后零偏数据估计的衰减曲线.可以看出两者在目标层均有大的衰减.由叠前数据估计的衰减曲线看出,在煤层附近有衰减,指示煤层附近可能有储层,而从叠后数据估计的衰减曲线上无法做出这一判断.
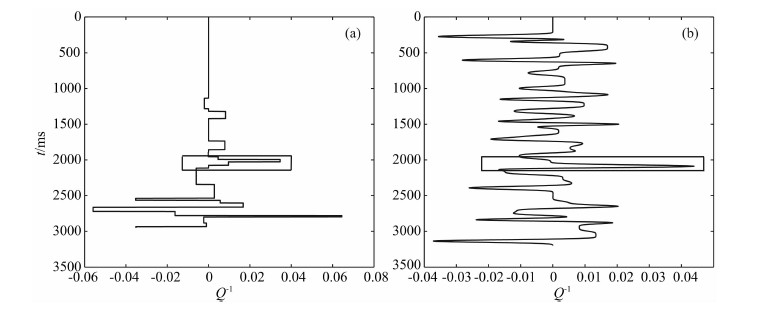
|
图 22 叠前CMP资料估计的衰减曲线(a)和叠后零偏资料估计的衰减曲线(b) Fig. 22 (a) The estimated Q-curve from pre-stack CMP data and (b) the estimated Q-curve from post-stack zero-offset record |
本文提出了用WEPIF法估计叠前CMP资料介质品质因子的方法,同时提出一种利用相关性估计层位信息的方法,并发展了适合常相位子波的EPIFVO(子波包络峰值处瞬时频率随偏移距变化)法.从EPIFVO的实现过程可以看出,由于需要用不同偏移距处的值进行线性回归,且多层介质等效为单层介质,因此该方法适用于层状均匀介质,对速度和Q值存在横向变化的情况,需要用更精细的方法来刻画地下介质构造.本文通过射线法正演生成叠前CMP数据,分别采用逐层递推方式与相邻两层直接求取方式用WEPIF法估计了Q值,结果表明逐层递推方式的误差累积效应更明显;并用斜率法估计了衰减;分析了误差产生的原因;本文还讨论了斜率对同相轴调谐的判断作用;通过实际资料算例表明,叠前CMP资料由于不受叠加效应及NMO拉伸效应等的影响,估计Q值更精确,更有利于含气性预测.
本文提出的方法在信噪比较低时同相轴难以精确追踪;线性回归时人机交互的主观影响较大,这些因素影响Q值估计精度,需要进一步研究.
致谢感谢长庆油田提供实际资料.
| [1] | 李庆忠. 走向精确勘探的道路. 北京: 石油工业出版社, 1993 . Li Q Z. The Road of Accurate Exploration (in Chinese). Beijing: Petroleum Industry Press, 1993 . |
| [2] | Ricker N. The form and laws of propagation of seismic wavelets. Geophysics , 1953, 18(1): 10-40. DOI:10.1190/1.1437843 |
| [3] | Winkler K W, Nur A. Seismic attenuation: Effects of pore fluids and frictional-sliding. Geophysics , 1982, 47(1): 1-15. DOI:10.1190/1.1441276 |
| [4] | Sheriff R E, Geldart L P. Exploration Seismology. London: Cambridge University Press, 1995 . |
| [5] | Yilmaz Ö. Seismic Data Processing. Tulsa Oklahoma: Society of Exploration Geophysicists, 1991. |
| [6] | 王小杰, 吴国忱.基于叠前地震资料地层吸收参数提取方法研究[硕士论文].山东:中国石油大学(华东), 2009. Wang X J, Wu G C. The study on methods of layer absorbing parameters extraction based on prestack seismic data[Master's thesis](in Chinese). Shandong: China University of Petroleum (East China), 2009. http://cdmd.cnki.com.cn/Article/CDMD-10425-2009222393.htm |
| [7] | Zhang C, Ulrychz T J. Estimation of quality factors from CMP record. Geophysics , 2002, 67(5): 1542-1547. DOI:10.1190/1.1512799 |
| [8] | Zhang C J, Ulrych T. Seismic Absorption Estimation and Compensation. American Geophysical Union, 2008, S11D-03. |
| [9] | 高静怀, 汪文秉, 朱光明, 等. 地震资料处理中小波函数的选取研究. 地球物理学报 , 1996, 39(3): 392–400. Gao J H, Wang W B, Zhu G M, et al. On the choice of wavelet functions for seismic data processing. Chinese J. Geophys. (in Chinese) , 1996, 39(3): 392-400. |
| [10] | 高静怀, 杨森林. 利用零偏移VSP资料估计介质品质因子方法研究. 地球物理学报 , 2007, 50(4): 1198–1209. Gao J H, Yang S L. On the method of quality factors estimation from zero-offset VSP data. Chinese J. Geophys. (in Chinese) , 2007, 50(4): 1198-1209. |
| [11] | Gao J H, Yang S L, Wang D X. Estimation of quality factor Q from the instantaneous frequency at the envelope peak of a seismic signal. Journal of Computational Acoustics , 2011, 19(2): 155-179. DOI:10.1142/S0218396X11004390 |
| [12] | Gao J H, Yang S L, Wang D X, et al. Quality factors estimation using wavelet's envelope peak instantaneous frequency. 79th Annual International meeting, SEG, Expanded Abstracts, 2009: 2457-2461. |
| [13] | Barnes A E. Instantaneous spectral band-width and dominant frequency with applications to seismic reflection data. Geophysics , 1993, 58(3): 419-428. DOI:10.1190/1.1443425 |
| [14] | Pujol J. Elastic Wave Propagation and Generation in Seismology. London: Cambridge University Press, 2003 . |
| [15] | Aki K, Richards P G. Quantitative Seismology: Theory and Methods. San Francisco W. H.: Freeman and Co., 1980 . |
| [16] | Barnes A E. Instantaneous frequency and amplitude at the envelop peak of a constant-phase wavelet. Geophysics , 1991, 56(7): 1058-1060. DOI:10.1190/1.1443115 |
| [17] | 陆基孟. 地震勘探原理. 北京: 石油大学出版社, 2001 . Lu J M. Seismic Survey Theory (in Chinese). Beijing: China University of Petroleum Press, 2001 . |
| [18] | Hubral P, Krey T, Larner K L, et al. Interval Velocities from Seismic Reflection Time Measurements. Tulsa Oklahoma: Society of Exploration Geophysicists, 1980. |
| [19] | Yang S L, Gao J H. Seismic quality factors estimation from spectral correlation. IEEE Geoscience and Remote Sensing Letters , 2008, 5(4): 740-744. DOI:10.1109/LGRS.2008.2004507 |
| [20] | 高静怀, 杨森林, 王大兴. 利用VSP资料直达波的包络峰值处瞬时频率提取介质品质因子. 地球物理学报 , 2008, 51(3): 853–861. Gao J H, Yang S L, Wang D X. Quality factor extraction using instantaneous frequency at envelope peak of direct waves of VSP data. Chinese J. Geophys. (in Chinese) , 2008, 51(3): 853-861. |
| [21] | Gao J H, Li Y M, Chen W C. On the instantaneous attributes analysis of seismic data via wavelet transform. 68th Annual meeting, SEG, Expanded Abstracts, 1998: 1084-1087. |
| [22] | 杨森林, 高静怀.最小平方反演提高VSP资料Q值估计的精度和稳定性.第25届中国地球物理学会年会, 2009: 151. Yang S L, Gao J H. Least-square inversion in improving the resolution and stability of quality-factor estimation for VSP records. 25th Chinese Geophysical Society, 2009: 151. |
| [23] | 高静怀, 杨森林, 王大兴等.利用地震信号的包络峰值瞬时频率估计介质因子.//中国应用地球物理论文选集.上海:上海科学技术出版社, 2009: 373-390. Gao J H, Yang S L, Wang D X, et al. Quality factor estimation using instantaneous frequencies at envelope peaks of seismic signals. China Applied Geophysics Collection of Treatises. Shanghai: Shanghai Scientific and Technical Publishers, 2009: 373-390. |
| [24] | 杨森林.地震衰减估计方法研究及应用[博士论文].西安:西安交通大学, 2010. Yang S L. Research on the estimation method of seismic attenuation and its application[Ph. D. thesis](in Chinese). Xi'an: Xi'an Jiaotong University, 2010. http://www.oalib.com/references/18988322 |
 2013, Vol. 56
2013, Vol. 56



