2. 中海油研究总院, 北京 100027
2. CNOOC Research Institute, Beijing 100027, China
逆时偏移最初起源于20世纪80年代[1-4],当时由于计算能力的不足限制了逆时偏移的发展.伴随着计算机技术的不断进步,逆时偏移因其不存在偏移倾角的限制,能够对各种具有不同传播方向的波(反射波、绕射波、棱柱波和回转波等)进行成像,近年来重新成为地球物理学界的研究热点.当前,得益于高性能并行计算技术的发展[5-7]和逆时偏移存储瓶颈的解决[7-10],逆时偏移技术开始逐步从理论研究过渡到实际应用,越来越多的工业生产开始做逆时偏移.
逆时偏移需要通过求解双程波动方程[11-14]来分别构建震源和检波波场,然后利用成像条件进行成像.然而,在使用双程波动方程进行波场构建中遇到波阻抗分界面就会发生反射,导致在成像过程中形成了低波数噪音[15].无论是何种形式的逆时偏移(声波逆时偏移[1-3, 16]、弹性波逆时偏移[17-19]和各向异性逆时偏移[20-21]),这种低波数噪音都是其特有的、最主要的噪音,严重干扰了成像剖面的质量和进一步的处理和解释.
早期的低波数噪音压制方法主要是在使用双程波动方程进行波场构建中尽量避免发生背向反射,比如使用无反射双程波动方程[22]、平滑速度场[23]、沿着反射界面布置吸收因子[24]等.但是这类方法不能彻底的避免背向反射,而且在一定程度上抛弃了“双程波”的优势,不能对一些具有多个传播方向的波(如回转波、棱柱波等)进行成像.目前新发展的低波数噪音压制方法采取的做法不是压制背向反射,而是进行选择性成像,比如方向分解成像条件[25-26]、角度衰减因子成像条件[27-28]、成像后滤波[8, 29-31]等.这些方法都在一定程度上具有较好的低波数噪音压制效果.但是,由于每种方法都具有各自的特点和适用性,应根据实际的应用条件和成像需求进行合理的选择[32-33].因此,如何在这众多的低波数噪声压制方法之中进行最优化的选择是逆时偏移实际应用时需要解决的关键问题之一.
为此,本文在全面分析逆时偏移中低波数噪音本质的基础上,对目前常用的各种去噪方法进行了归类和分析,总结了每种方法的适用条件和去噪的优缺点,给出了不同成像要求和实现条件下最佳去噪方法抉择策略.并依据选取几种最优的去噪方法组合方案进行了模型测试.
2 低波数噪音的本质逆时偏移主要包括两步:使用双程波动方程构建震源波场S(m,t)和检波波场R(m,t),然后利用互相关成像条件[34]进行成像,得到空间位置m有关的成像结果I(m):
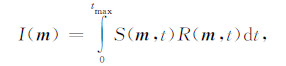
|
(1) |
其中,m代表空间位置,tmax代表记录的最大时刻,S(m,t)和R(m,t)分别代表震源和检波波场,I(m)代表空间位置m处成像结果.
由于逆时偏移采用双程波动方程,同时允许两个相反方向波的传播.无论是震源波场还是检波波场,在外推重构中,遇到波阻抗分界面都会发生背向反射.因此使用互相关成像条件进行成像时,不可避免的包括如下情形:
(1)正向传播的震源波场与正向传播的检波波场之间的互相关;
(2)背向反射的震源波场与背向反射的检波波场之间的互相关;
(3)正向传播的震源波场与背向反射的检波波场之间的互相关;
(4)背向反射的震源波场与正向传播的检波波场之间的互相关.
其中第(1)和第(2)种情形所形成的结果是期望的成像值.而第(3)和第(4)种情形所形成的结果则为不期望的低波数噪音.
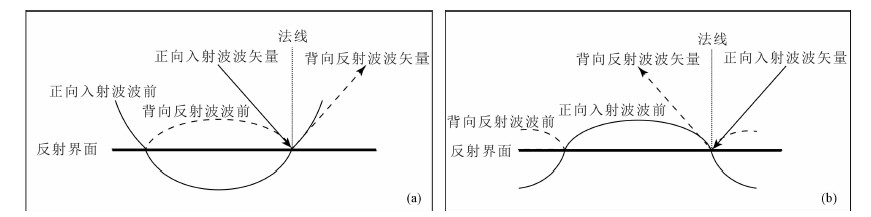
如图 1所示,(a)代表逆时偏移中构建的震源波场,(b)代表逆时偏移中构建的检波波场.图中细实线表示正向传播的震源波场和检波波场;长虚线表示背向反射的震源波场和检波波场;粗实线为反射界面;点线表示法线.图中直线箭头代表波矢量,圆弧代表波前面.图 1中细实线表示的波前之间互相关以及长虚线表示的波前之间互相关(即第(1)和第(2)种情形)得到成像反射界面,细实线表示的波前与长虚线表示波前互相关(即第(3)和第(4)种情形)得到低波数噪音.低波数噪音集中表现为传播方向相反的波前面的互相关,对应波矢量的夹角为180°(对应的入射角为90°).但实际成像中,只要波矢量的夹角很大(接近80°)都是无物理意义的成像结果,均表现为低波数噪音.
|
图 1 逆时偏移中震源和检波波场传播示意图 (a)震源波场的波前面和传播方向;(b)检波波场的波前面和传播方向. Fig. 1 The schematic of the wave propagation of source and receiver wavefields in RTM (a) The wavefront and propagation direction of source wavefield; (b) The wavefront and propagation direction of receiver wavefield |
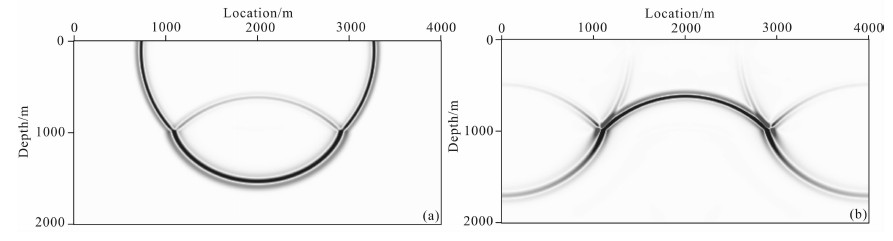
图 2展示了与图 1相对应的RTM中实际构建的震源和检波波场,其中(a)为震源波场,(b)为检波波场.从图中可以看出,由于使用了双程波动方程,因此在震源波场和检波波场中均出现背向反射,其中背向反射的震源波场的波前表现为能量较强的反射圆弧,而背向反射的检波波场的波前面因有限范围的地面观测孔径表现为向边界弯曲的弧形状.因此在互相关成像中,第(4)种情形背向反射的震源波场与正向传播的检波波场之间的互相关产生的能量较强,是低波数噪音的主要来源;而第(3)种情形中正向传播的震源波场与背向反射的检波波场之间的互相关产生的能量较弱,贡献了少部分低波数噪音.
|
图 2 逆时偏移中构建的震源和检波波场 (a)震源波场;(b)检波波场. Fig. 2 The reconstructed source and receiver wavefields in RTM (a) Source wavefield; (b) Receiver wavefield. |
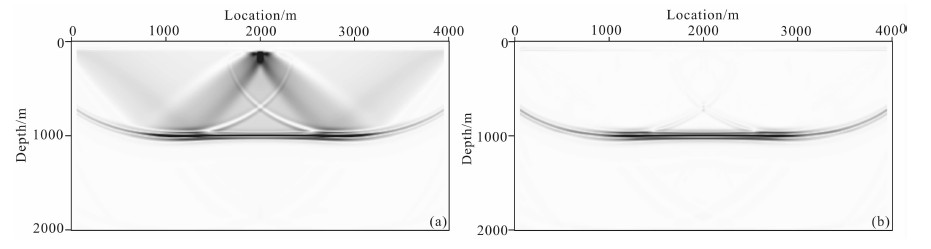
图 3给出了与图 1和图 2所对应的单层反射界面模型RTM成像结果.其中(a)被低波数噪音严重污染,而去噪后的成像结果(b)清晰准确.
|
图 3 逆时偏移成像结果 (a)含低波数噪音;(b)去噪后. Fig. 3 The RTM images (a) Image includes low-wavenumber noise; (b) Image without low-wavenumber noise. |
通过对比分析得出如下结论:低波数噪音本质上是因使用双程波动方程引起的震源波场与检波波场波矢量的夹角为超大角度(尤其是散射角为180°或者说是入射角为90°)时震源波场与检波波场之间的互相关产生的无物理意义的成像结果.上述分析结果也适用于激发时间成像条件[4]的逆时偏移,因为激发时间成像条件是公式(1)中震源波场振幅值等于1时的特例.
3 低波数噪音压制方法根据低波数噪音产生的本质,相应的压制方法要围绕下述两个方面展开:(1)在构建波场中避免发生背向反射;(2)在波场构建中进行选择性成像.
3.1 第一类噪音压制方法第一类的压制策略方法的核心是在构建波场中避免发生背向反射.主要方法有:
3.1.1 使用无反射双程波动方程进行波场构建Baysal等[22]使用恒定波阻抗代入波动方程,得到了无反射波动方程.无反射波动方程虽然可以完全消除法向入射时地下界面产生的反射,但是随着偏移距的增大,仍然会出现反射.该方程能精确适用于叠后的逆时偏移,却不适用于叠前逆时偏移.
3.1.2 波场构建中使用平滑的速度场Loewenthal等[23]使用矩形算子在大于一个波长的范围内进行平滑慢度场,以消除双程波逆时外推中的背向反射.但实际上,单纯的平滑慢度场并不能完全消除背向反射和低波数噪音,并会改变地震波传播的运动学特征,使得成像位置发生偏差.
3.1.3 在波场构建中沿反射界面布置方向吸收因子Fletcher等[24]使用双程波动方程,在反射界面上引入一个方向阻尼项作为边界条件,在逆时重构波场中消除背向反射,从而压制其所带来的噪音.但是,这种方法在实际操作处理时要人工选择地下界面,不适用于复杂模型.
综上分析,第一类压制方法去噪效果都不是特别理想.更重要的是这类方法在波场构建中不能构建出具有多个传播方向的波(如回转波、棱柱波等),因此就无法对产生这种波的相关构造(比如高陡倾角岩丘侧翼等)进行成像.尽管如此,生产中常常采用在波场构建中使用平滑的速度场压制低波数噪音.虽然这种方法不能从根本上消除低波数噪音,但因其实现起来方便、简单,还是被许多人应用.需要注意的是,对于速度场的平滑要适中.平滑程度太小会影响去噪效果;而平滑程度太大,会增大成像位置的偏差,尤其是对强波阻抗反射界面的影响最为明显.
3.2 第二类噪音压制方法第二类的压制策略方法的核心是进行选择性成像.主要的手段主要包括两个方面:一是在成像过程中根据波传播的方向选择中小角度传播的波进行成像;二是在成像后进行滤波处理.对于在成像过程中的压制方法,主要使用方向分解互相关成像条件或角度衰减因子互相关成像条件.对于在成像后压制方法,主要包括:一维滤波、多维滤波、中小角度的角度域道集叠加和基于最小平方思想的振幅补偿等方法.
3.2.1 方向分解成像条件方向分解成像条件由Liu等提出[25-26].它相对于反射界面的切线方向,把每个反射点处的波场分解为相对于反射界面向上传播的波场和向下传播的波场:
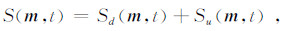
|
(2) |
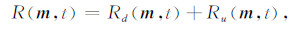
|
(3) |
其中S(m,t)和R(m,t)分别代表了震源和检波波场,下标d和u分别代表相对于反射界面向下传播的波场和向上传播的波场,然后选择前文中第(1)和第(2)种互相关情形进行互相关成像:
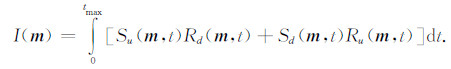
|
(4) |
具体实现时,需要对波场沿某一方向上进行分解.为了提高算法实现的效率,Liu等[26]给出了(4)式的另一种等价形式:
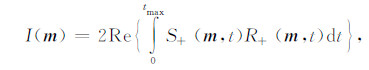
|
(5) |
其中,
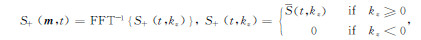
|
(6) |
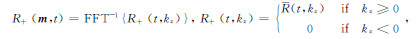
|
(7) |
S(t,kz)和R(t,kz)分别是S(m,t)和R(m,t)沿z方向的一维FFT正变换.
3.2.2 角度衰减因子互相关成像条件对中小角度的成像值进行选择性成像,可以在成像条件中构造大角度衰减因子压制超大角度的无意义成像结果,即
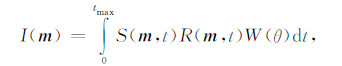
|
(8) |
其中大角度衰减因子W(θ)可以由能流密度矢量构建.Yoon等[27]首先利用能流密度矢量估算散射角:
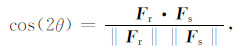
|
(9) |
然后构建如下形式的衰减因子:
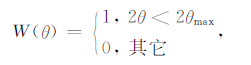
|
(10) |
其中2θmax是人工给出的最大的散射角.由于Yoon等[27]给出的角度衰减因子截断效应过于明显,Costa等[28]给出了另外一种形式的角度衰减因子:
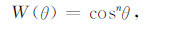
|
(11) |
Costa等[28]通过实例说明选择n≥3去噪效果较好.
实际上,这种方法的核心是通过能流密度矢量估算散射角,然后构造角度衰减因子.角度衰减因子的构造方式多种多样,可以不仅限于上述文献中所给出的形式,完全可以根据需要来限制最大角度和选择不同边界平滑衰减函数,从而构造出其它形式的角度衰减因子.但是需要注意的是,角度衰减因子的精度依赖于能流密度矢量的精度.在某一时间和空间位置上,能流密度矢量只能表征地震波在该点处的一个主要的传播方向[18],当空间上某一点具有多个传播方向的地震波时,能流密度矢量的精度会降低.因此,对于特别复杂的构造,角度衰减因子互相关成像条件的去噪效果会降低.
3.2.3 角度域道集叠加通过对低波数噪音的分析中可知,其产生的根本原因之一是震源波场与检波波场的波矢量的夹角为超大角度时进行互相关的结果.因此低波数噪音是跟角度相关的,故可以在角度域道集上进行滤波处理,对大角度的成像结果进行衰减,选择中小角度范围内的成像结果进行叠加:
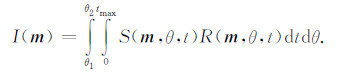
|
(12) |
在实现时,首先要计算地下每个位置处的角度域道集,然后在角度域道集上选择适当的角度阈值,对小于这一角度的所有成像值进行叠加,得到最终的成像剖面.由于需要对地下每个点都计算角度域道集,因此实际上该方法的计算代价较高,实现成本较大.
3.2.4 一维滤波采用一维(1D)滤波是指在成像后,直接对成像剖面采用1D形式的滤波压制低波数噪音:
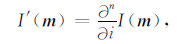
|
(13) |
其中i={x,y,z},n为阶数.这种一维形式的滤波简单实用、效果明显,但是有一个严重的缺陷:损害了非求导方向的同相轴[29].如对于一个x(水平)和z(垂直)方向的2D成像剖面,如果选择对于z(垂直)方向进行求导,那么滤波后的剖面中将不包含x(水平)的同相轴.因此实际应用时,应考虑实际成像构造的分布特征.
3.2.5 多维滤波针对一维滤波的缺陷,采用多维滤波可以完美的解决.多维滤波器形式为
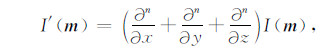
|
(14) |
当n=2时,即为Laplace滤波[30].
然而诸如Laplace等多维滤波也存在一定缺陷,它使得成像剖面中同相轴振幅大小和频率成分发生变化,而且会带来额外的高频噪音.滤波器的维数越高,引入的高频噪音越多.为了解决地震成像同相轴的相位的变化,张宇等[31]分析了Laplace滤波的物理意义,并给出了一种Laplace振幅校正的方法.在波数域,Lapalce滤波的形式为
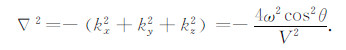
|
(15) |
从(15)式可以看出,Laplace滤波的本质是以cos2θ对成像剖面进行角度衰减.但是滤波的同时也对成像剖面的振幅带来-4/V2的影响,频率成分带来ω2的影响.为了这种影响进行补偿,需要在偏移之前对输入的地震剖面进行-1/ω2的补偿,和在成像滤波之后对振幅进行V2/4的标定.然而,因为在偏移之前对炮记录进行补偿和偏移之后的Laplace滤波是配套使用的,所以在这个过程之中不适合求取角度域道集.
3.2.6 最小平方思想的振幅补偿另外一种噪音的压制方法是基于最小平方理论展开的.对于给定的一个正演算子A和接收到地震数据d,来求解模型m,使得
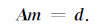
|
(16) |
通常的偏移算子为正演算子A的伴随矩阵A′,而不是逆矩阵.因此偏移成像的结果实际为
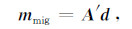
|
(17) |
正是由于正演算子A严格意义下不一定存在逆矩阵,因此,求解模型是最小平方意义下的最优解
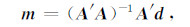
|
(18) |
而实际上进行最小平方偏移,还必须考虑数据的平滑,因此最小平方的解通常为
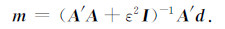
|
(19) |
通过比较常规偏移的结果和最小平方解,可以发现最小平方解实质是在常规偏移基础上的振幅补偿:
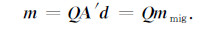
|
(20) |
因此,只要在正常偏移的基础上使用正规化矩阵Q对初次偏移的结果mmig进行滤波即可得到高信噪比的、最小平方解.理论上,直接求解矩阵Q是非常困难的,需要通过预测误差滤波[35]对矩阵A进行估算,而且反演过程中容易出现不稳定.Guitton等[29]通过求解预测误差滤波器,对逆时偏移的结果进行最小平方滤波,消除了低波数噪音.
另外,也可以通过对矩阵Q进行简化,得到相对稳定的结果,然后利用(20)式所体现出的振幅补偿的思想来压制逆时偏移中的低波数噪音.逆时偏移过程中采用的震源波场和检波波场的照明补偿就属于其中的一种.震源波场照明补偿通过求解震源的照明来代替矩阵Q:
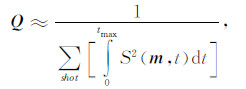
|
(21) |
而检波波场照明补偿则通过求解检波波场的照明来代替矩阵Q:
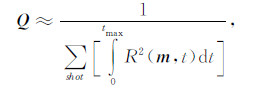
|
(22) |
或者同时使用震源波场照明补偿和检波波场照明补偿,通过震源波场和检波波场的照明来代替矩阵Q:
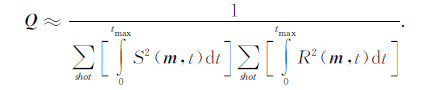
|
(23) |
但是需要注意的是采用震源或者检波波场照明补偿来代替正规化矩阵Q的做法,是一种非常粗略的近似.它仅能在一定程度上压制逆时偏移中的低波数噪音,很大程度上偏离了最小平方意义下的解.因此,照明补偿得到的结果仅仅是一种振幅补偿后的成像结果,而不是严格意义下的真振幅成像结果.
许多学者研究了带有震源照明补偿的成像条件[36-39],对于不同的照明补偿方式(震源照明补偿,检波照明补偿,以及震源和检波照明补偿),其对于噪音的压制程度和真振幅的逼近程度也各不相同.对于噪音压制程度方面,同时采用震源和检波照明补偿对于低波数噪音压制效果最好.而对于真振幅的逼近程度方面,在炮域带有震源照明补偿的互相关成像条件对于真振幅的逼近程度更好.
4 低波数噪音压制方法最优化抉择策略上述这些低波数噪声压制方法都有各自的特点和适用性,而且每种方法的具体实现环境也不同,不能盲目的进行使用.应该考虑具体的实现条件和成像的需求,比如低波数噪音去除过程与RTM实现过程的关系、低波数噪音去除的程度、成像构造复杂程度、成像结果的保幅性、以及RTM适用的域(炮域或角度域)等,对去噪方法进行合理的搭配和选择.具体的抉择策略如图 4所示.
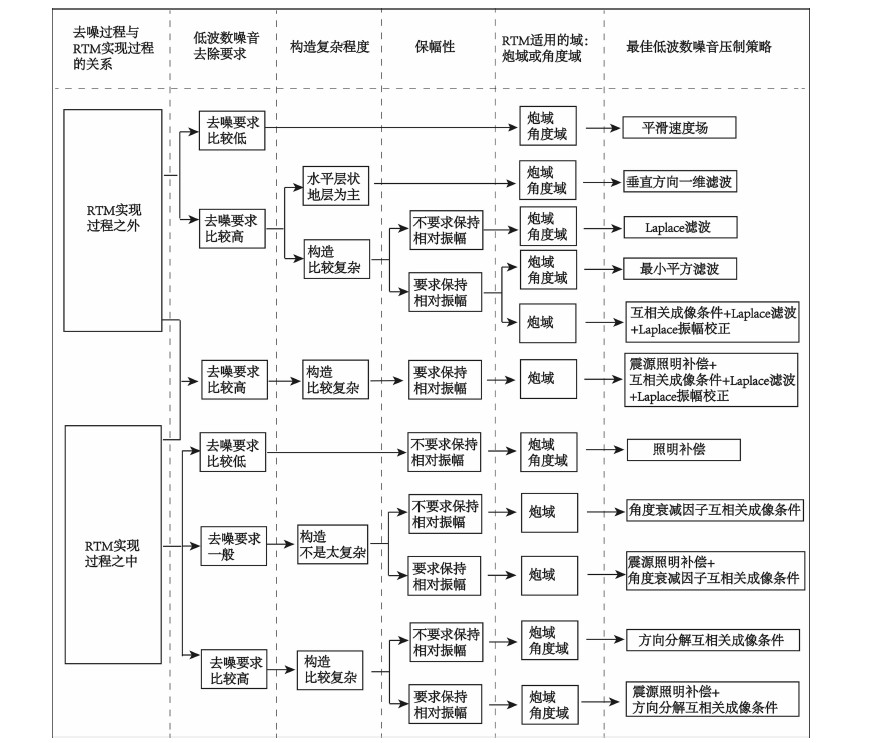
|
图 4 最优化低波数噪音压制抉择策略 Fig. 4 The optimal strategy of noise suppression methods |
在RTM实现过程之外(包括实现之前和之后)对低波数噪音进行压制,可以选择平滑速度场或者滤波的方法.其中低波数噪音去除程度要求比较低时,可以选择平滑速度场.平滑速度场简单、实用,但使用时需要注意速度场的平滑程度不能太大,否则会影响成像剖面的精度;低波数噪音去除程度要求比较高时,可以选择一维滤波、Laplace滤波或最小平方滤波.如果构造主要由水平层状地层组成,成像目标没有诸如复杂岩丘等特别陡的倾角地层,可以仅选择一维垂直方向上的滤波;如果构造比较复杂,如成像目标包括陡倾角地层,建议使用Laplace滤波.根据成像结果的保幅性要求又可以分为两种情况:如果成像要求仅是构造成像,对振幅保持要求不高,仅使用Laplace滤波而不需进行Laplace振幅校正;如果成像要求保持相对振幅,可以使用Laplace滤波加Laplace振幅校正,或者使用最小平方滤波.进行Laplace振幅校正时,需要对原始的炮记录进行两次积分补偿,然后在偏移后进行Laplace滤波和振幅标定.但是这种Laplace振幅补偿修改了原始输入的炮记录,因此在偏移中不适合进行角度域有关的处理,如在偏移中抽取角度域道集等.因此,如果需要抽取角度域道集或者进行偏移速度分析,不建议使用这种Laplace振幅校正方法.
在RTM实现过程之中对低波数噪音压制可以使用角度衰减因子互相关成像条件、方向分解互相关成像条件和照明补偿.低波数噪音去除程度要求比较低时,如仅压制一部分低波数噪音使得成像结果可以见,可以仅仅使用照明补偿;低波数噪音去除程度要求比较高,同时成像目标构造相对简单,可以使用带有角度衰减因子的成像条件;当要求对低波数噪音去除程度比较高时,并且成像目标包括比较复杂的构造,建议选择方向分解成像条件.当成像目标要求相对的保持真振幅特性时,建议在当前去噪方法的基础上搭配震源照明补偿,如把震源照明补偿搭配角度衰减因子互相关成像条件和方向分解互相关成像条件.当需要进行与角度域有关的处理时,建议使用方向分解互相关成像条件,而不是角度衰减因子互相关成像条件.因为角度衰减因子互相关成像条件在成像过程中对大角度的成像值进行了压制,得到的角度域的偏移结果实际上是角度域切除滤波之后的,不能真实反映原始的角度域成像信息.
当然,也可以在RTM实现过程之中和之后同时使用压制低波数噪音的方法,如可以使用震源照明补偿、互相关成像条件、Laplace滤波和Laplace振幅校正.这种方案去噪效果较好,并且能够得到保幅性较好的成像剖面.但是需要注意的是这种方案同样也不适合于角度域有关的处理.
5 模型测试为了考察不同去噪方案的效果和适用性,使用简单的四层水平模型进行单炮偏移测试,和使用复杂的Sigsbee2a模型进行多炮偏移测试,并使用如下6种去噪方案进行去噪:
(1)互相关成像条件;
(2)互相关成像条件、震源照明补偿;
(3)角度衰减因子互相关成像条件、震源照明补偿;
(4)方向分解互相关成像条件、震源照明补偿;
(5)互相关成像条件、震源照明补偿、Laplace滤波;
(6)互相关成像条件、震源照明补偿、Laplace滤波、Laplace滤波振幅校正.
5.1 四层模型设计如图 5所示的四层水平模型,模型的大小是4000×2500m,四层速度分别为2500m/s、2700m/s、2916m/s、3149.3m/s,使三个反射界面法向入射处的反射系数相等.震源埋深为x=2000m,z=100m,使用准确的速度场对单炮进行逆时偏移,偏移中使用的网格大小是10×10m.使用上述6种去噪方案进行去噪,抽取法向入射处(x=2000 m)单道偏移结果,对6种方法得到的单道偏移结果归一化后进行对比.
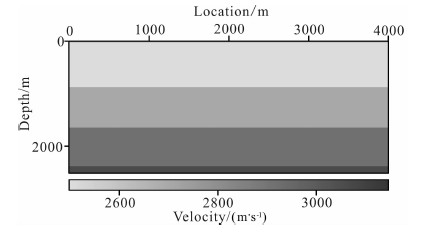
|
图 5 四层水平模型 Fig. 5 Four-horizontal-layer model |
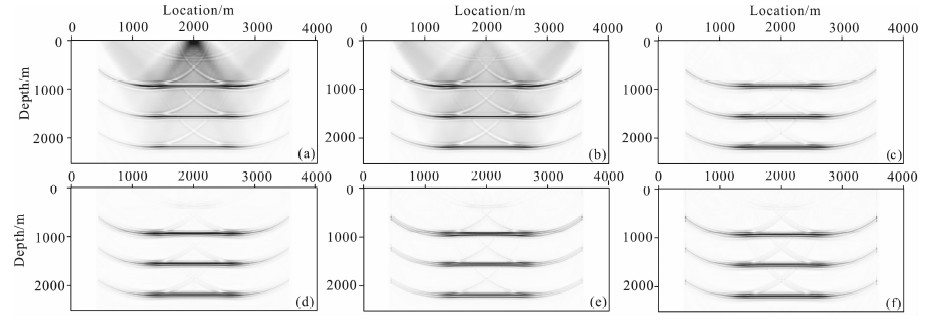
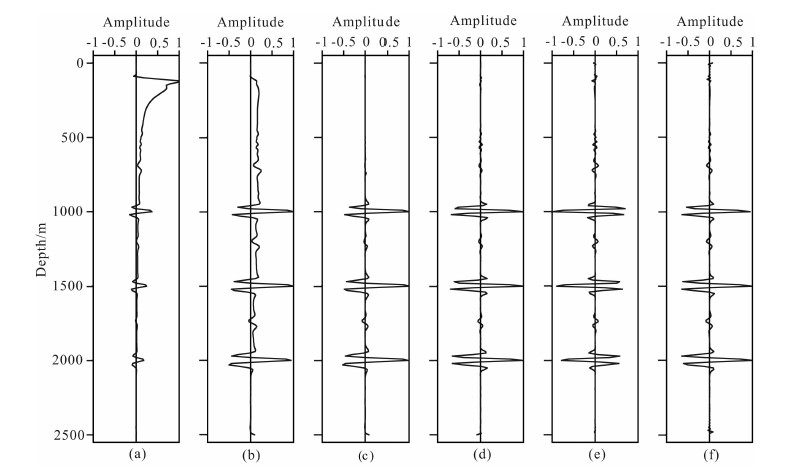
图 6显示了6种去噪方案对应的单炮RTM结果,图 7对应地给出了法向入射处单道RTM结果.由偏移结果可见,仅由互相关成像条件得到的结果含有大量的低波数噪音,并且三个反射界面处的振幅依次减弱,不能保持正确的相对振幅强弱关系.而带有震源照明补偿的成像条件基本上恢复了三层反射界面振幅的相对关系.在去噪效果上,带有角度衰减因子的互相关成像条件、方向分解互相关成像条件和Laplace滤波则去除了低波数噪音.因此,在这三种去噪方法的前提下同时配合使用震源照明补偿可以得到质量较好的成像结果.
|
图 6 四层水平模型单炮RTM结果 (a)互相关成像条件;(b)互相关成像条件、震源照明补偿;(c)角度衰减因子互相关成像条件、震源照明补偿;(d)方向分解互相关成像条件、震源照明补偿;(e)互相关成像条件、震源照明补偿、Laplace滤波;(f)互相关成像条件、震源照明补偿、Laplace滤波、Laplace滤波振幅校正. Fig. 6 Single-shot RTM image of four-layer model (a) Crosscorrelation imaging condition; (b) Crosscorrelation imaging condition, source illumination compensation; (c) Crosscorrelation imaging condition using angle decay factor, source illumination compensation; (d) Crosscorrelation imaging condition using wavefield decomposition, source illumination compensation; (e) Crosscorrelation imaging condition, source illumination compensation, Laplace filter; (f) Crosscorrelation imaging condition, source illumination compensation, Laplace filter, Laplace amplitude correction. |
|
图 7 四层水平模型法向入射处单道RTM结果 (a)互相关成像条件;(b)互相关成像条件、震源照明补偿;(c)角度衰减因子互相关成像条件、震源照明补偿;(d)方向分解互相关成像条件、震源照明补偿;(e)互相关成像条件、震源照明补偿、Laplace滤波;(f)互相关成像条件、震源照明补偿、Laplace滤波、Laplace滤波振幅相位校正. Fig. 7 Single-trace RTM image of normal incidence in four-layer model (a) Crosscorrelation imaging condition; (b) crosscorrelation imaging condition, source illumination compensation; (c) Crosscorrelation imaging condition using angle decay factor, source illumination compensation; (d) Crosscorrelation imaging condition using wavefield decomposition, source illumination compensation; (e) Crosscorrelation imaging condition, source illumination compensation, Laplace filter; (f) Crosscorrelation imaging condition, source illumination compensation, Laplace filter, Laplace amplitude correction. |
其中Laplace滤波虽然除了低波数噪音,但是在一定程度上改变了三层反射界面成像振幅的相对大小并且极性发生反转,如图 6e和图 7e,而经过振幅校正后的Laplace滤波则在一定程度上弥补了Laplace滤波对成像剖面的影响,如图 6f和图 7f.图 7f中与e相比,三层反射界面成像振幅的相对大小得到了正确的补偿,极性也与互相关成像条件得到的结果相一致.
5.2 Sigsbee2a模型使用Sigsbee2a模型对上述的6种去噪方法进行多炮RTM测试.Sigsbee2a模型如图 8所示.使用准确的速度场进行逆时偏移,震源从3.048km开始,到27.432km结束,炮间距121.92m,共201炮.
|
图 8 Sigsbee 2a模型 Fig. 8 Sigsbee 2a model |
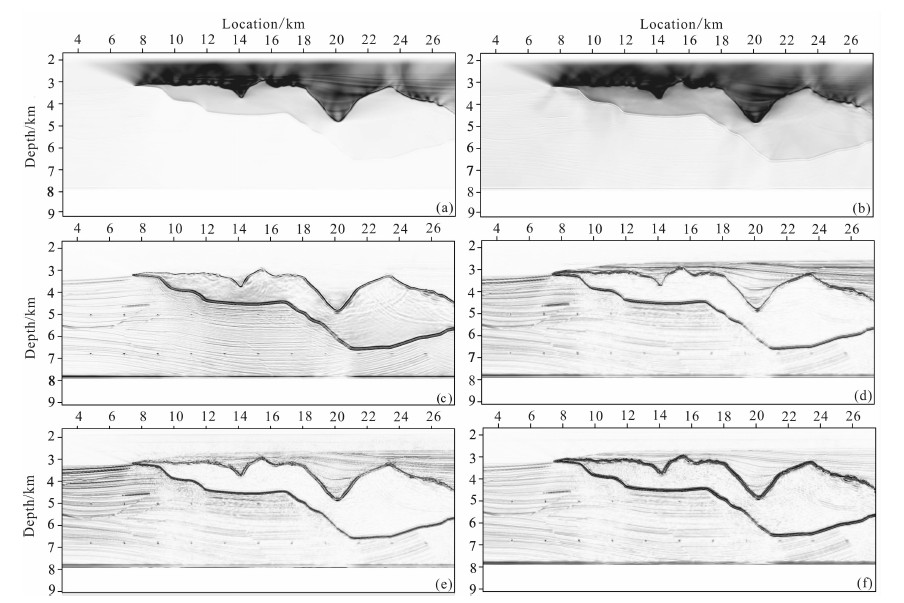
图 9a显示了仅由互相关成像条件得到的RTM成像结果,岩丘强反射界面上方低波数噪音严重屏蔽了深层构造.图 9b显示了带有震源照明补偿的互相关成像条件得到的RTM成像结果,虽然在一定程度上弥补了深层的能量,但是低波数噪音依然很强.图 9c显示了带有震源照明补偿的角度衰减因子互相关成像条件得到的RTM成像结果,对于该复杂模型,角度衰减因子成像条件去除了大部分低波数噪音,但还有少量残留.其原因正如上文分析中复杂模型中能流密度矢量的计算精度降低导致去噪效果的下降,说明该去噪方法对于复杂模型略显不足. 图 9d显示了带有震源照明补偿的方向分解互相关成像条件得到的RTM成像结果,可见方向分解互相关成像条件有效地去除了低波数噪音,成像结果清晰、准确.图 9e显示了在带有震源照明补偿的互相关成像条件得到的RTM成像剖面(即图 9b)上进行Laplace滤波后的结果,可见Laplace滤波也有效地去除了低波数噪音,但是也引入了一些额外影响:一是改变了整个剖面的振幅强弱关系,二是引入了一些高频噪音.图 9f是在e的基础上进行Laplace振幅校正后的结果,对比可见,Laplace振幅补偿基本上弥补了Laplace滤波对成像振幅的能量分布带来的影响,并且消除了因Laplace滤波带来的高频噪音.
|
图 9 Sigsbee2a模型多炮RTM结果 (a)互相关成像条件;(b)互相关成像条件、震源照明补偿;(c)角度衰减因子互相关成像条件、震源照明补偿;(d)方向分解互相关成像条件、震源照明补偿;(e)互相关成像条件、震源照明补偿、Laplace滤波;(f)互相关成像条件、震源照明补偿、Laplace滤波、Laplace滤波振幅相位校正. Fig. 9 Multi-shot RTM image of Sigsbee 2a model (a) Crosscorrelation imaging condition; (b) Crosscorrelation imaging condition, source illumination compensation; (c) crosscorrelation imaging condition using angle decay factor, source illumination compensation; (d) Crosscorrelation imaging condition using wavefield decomposition, source illumination compensation; (e) Crosscorrelation imaging condition, source illumination compensation, Laplace filter; (f) Crosscorrelation imaging condition, source illumination compensation, Laplace filter, Laplace amplitude correction. |
低波数噪音本质上是因使用双程波动方程引起的震源波场与检波波场波矢量的夹角为超大角度(尤其是散射角为180°或者说是入射角为90°)时震源波场与检波波场之间的互相关产生的无物理意义的成像结果.
第一类噪音压制方法采取的措施是在波场构建中来压制背向反射,但是去噪效果不是特别理想,并且不能对具有多个传播方向的波(如回转波、棱柱波等)同时进行成像.
第二类噪音压制方法通过进行选择性成像来压制低波数噪声.选择性成像主要包括两方面:一是在成像过程中根据波传播的方向进选择中小角度传播的波进行成像;二是在成像后进行滤波处理.
最佳的去噪方法的抉择策略是根据不同的实现环境和成像需求的条件下,对噪音压制方法进行合理的搭配.其中在RTM实现过程之后进行去噪,Laplace滤波加Laplace振幅校正是最佳选择;而在RTM实现过程之中进行去噪,震源照明补偿加方向分解互相关成像条件是最佳的选择.
| [1] | Whitmore N D. Iterative depth migration by backward time propagation//53rd Annual International Meeting, SEG, Expanded Abstracts, 1983, 2: 382-385. http://www.oalib.com/references/18988263 |
| [2] | McMechan G A. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting , 1983, 31(3): 413-420. DOI:10.1111/gpr.1983.31.issue-3 |
| [3] | Baysal E, Kosloff D D, Sherwood J W C. Reverse time migration. Geophysics , 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [4] | Chang W F, McMechan G A. Reverse-time migration of offset vertical seismic profiling data using the excitation-time imaging condition. Geophysics , 1986, 51(1): 67-84. DOI:10.1190/1.1442041 |
| [5] | Clapp R G, Fu H H, Lindtjorn O. Selecting the right hardware for reverse time migration. The Leading Edge , 2010, 29(1): 48-58. DOI:10.1190/1.3284053 |
| [6] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [7] | 李博, 刘红伟, 刘国锋, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报 , 2010, 53(12): 2938–2943. Li B, Liu H W, Liu G F, et al. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 2938-2943. |
| [8] | 刘红伟, 刘洪, 邹振, 等. 地震叠前逆时偏移中的去噪与存储. 地球物理学报 , 2010, 53(9): 2171–2180. Liu H W, Liu H, Zou Z, et al. The problems of denoise and storage in seismic reverse time migration. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2171-2180. |
| [9] | Symes W W. Reverse time migration with optimal checkpointing. Geophysics , 2007, 72(5): SM213-SM221. DOI:10.1190/1.2742686 |
| [10] | Clapp R G. Reverse time migration with random boundaries//79th Annual International Meeting, SEG, Expanded Abstracts, 2009, 28: 2809-2813. http://www.oalib.com/references/18988276 |
| [11] | Liu Y, Sen M K. A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation. Geophysics , 2010, 75(2): A1-A6. DOI:10.1190/1.3295447 |
| [12] | Liu Y, Sen M K. Finite-difference modeling with adaptive variable-length spatial operators. Geophysics , 2011, 76(4): T79-T89. DOI:10.1190/1.3587223 |
| [13] | 刘洋, 李承楚, 牟永光. 任意偶数阶精度有限差分法数值模拟. 石油地球物理勘探 , 1998, 33(1): 1–10. Liu Y, Li C C, Mou Y G. Finite difference numerical modeling of any even-order accuracy. Oil Geophysical Prospecting (in Chinese) , 1998, 33(1): 1-10. |
| [14] | 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报 , 2000, 43(3): 411–419. Dong L G, Ma Z T, Cao J Z, et al. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese) , 2000, 43(3): 411-419. |
| [15] | Yoon K, Marfurt K J, Starr W. Challenges in reverse-time migration//74th Annual International Meeting, SEG, Expanded Abstracts, 2004, 23: 1057-1060. |
| [16] | 何兵寿, 张会星, 韩令功, 等. 两种声波方程的叠前逆时深度偏移及比较. 石油地球物理勘探 , 2008, 43(6): 656–661. He B S, Zhang H X, Han L G, et al. Prestack reverse-time depth migration of two acoustic wave equation and comparison between both. Oil Geophysical Prospecting (in Chinese) , 2008, 43(6): 656-661. |
| [17] | Yan J, Sava P. Isotropic angle-domain elastic reverse-time migration. Geophysics , 2008, 73(6): S229-S239. DOI:10.1190/1.2981241 |
| [18] | Du Q Z, Zhu Y T, Ba J. Polarity reversal correction for elastic reverse time migration. Geophysics , 2012, 77(2): S31-S41. DOI:10.1190/geo2011-0348.1 |
| [19] | 杜启振, 秦童. 横向各向同性介质弹性波多分量叠前逆时偏移. 地球物理学报 , 2009, 52(3): 801–807. Du Q Z, Qin T. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 801-807. |
| [20] | Zhang H Z, Zhang Y. Reverse time migration in 3D heterogeneous TTI media//78th Annual International Meeting, SEG, Expanded Abstracts, 2008, 27: 2196-2200. |
| [21] | Zhang Y, Zhang H Z. A stable TTI reverse time migration and its implementation//79th Annual International Meeting, SEG, Expanded Abstracts, 2009, 28: 2794-2798. |
| [22] | Baysal E, Kosloff D D, Sherwood J W C. A two-way nonreflecting wave equation. Geophysics , 1984, 49(2): 132-141. DOI:10.1190/1.1441644 |
| [23] | Loewenthal D, Stoffa P L, Faria E L. Suppressing the unwanted reflections of the full wave equation. Geophysics , 1987, 52(7): 1007-1012. DOI:10.1190/1.1442352 |
| [24] | Fletcher R P, Fowler P J, Kitchenside P, et al. Suppressing unwanted internal reflections in prestack reverse-time migration. Geophysics , 2006, 71(6): E79-E82. DOI:10.1190/1.2356319 |
| [25] | Liu F Q, Zhang G Q, Morton S A, et al. Reverse-time migration using one-way wavefield imaging condition//77th Annual International Meeting, SEG, Expanded Abstracts, 2007, 26: 2170-2174. |
| [26] | Liu F Q, Zhang G Q, Morton S A, et al. An effective imaging condition for reverse-time migration using wavefield decomposition. Geophysics , 2011, 76(1): S29-S39. DOI:10.1190/1.3533914 |
| [27] | Yoon K, Marfurt K J. Reverse-time migration using the Poynting vector. Exploration Geophysics , 2006, 37(1): 102-107. DOI:10.1071/EG06102 |
| [28] | Costa J C, Neto F A S, Alcantara M R M, et al. Obliquity-correction imaging condition for reverse time migration. Geophysics , 2009, 74(3): S57-S66. DOI:10.1190/1.3110589 |
| [29] | Guitton A, Kaelin B, Biondi B. Least-squares attenuation of reverse-time-migration artifacts. Geophysics , 2007, 72(1): S19-S23. DOI:10.1190/1.2399367 |
| [30] | Youn O K, Zhou H W. Depth imaging with multiples. Geophysics , 2001, 66(1): 246-255. DOI:10.1190/1.1444901 |
| [31] | Zhang Y, Sun J. Practical issues of reverse time migration: True amplitude gathers, noise removal and harmonic-source encoding//70th EAGE International Annual Meeting, Extended Abstracts, 2008. F047. http://www.oalib.com/references/18988290 |
| [32] | 康玮, 程玖兵. 叠前逆时偏移假象去除方法. 地球物理学进展 , 2012, 27(3): 1163–1172. Kang W, Cheng J B. Methods of suppressing artifacts in prestack reverse time migration. Progress in Geophys. (in Chinese) , 2012, 27(3): 1163-1172. |
| [33] | 许璐, 孟小红, 刘国锋. 逆时偏移去噪方法研究进展. 地球物理学进展 , 2012, 27(4): 1548–1556. Xu L, Meng X H, Liu G F. Reverse time migration and removing artifacts. Progress in Geophys. (in Chinese) , 2012, 27(4): 1548-1556. |
| [34] | Claerbout J F. Toward a unified theory of reflector mapping. Geophysics , 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [35] | Claerbout J F. Multidimensional recursive filters via a helix. Geophysics , 1998, 63(5): 1532-1541. DOI:10.1190/1.1444449 |
| [36] | Kaelin B, Guitton A. Imaging condition for reverse time migration//76th Annual International Meeting, SEG, Expanded Abstracts, 2006, 25: 2594-2598. |
| [37] | Chattopadhyay S, McMechan G A. Imaging conditions for prestack reverse-time migration. Geophysics , 2008, 73(3): S81-S89. DOI:10.1190/1.2903822 |
| [38] | Schleicher J, Costa J C, Novais A. A comparison of imaging conditions for wave-equation shot-profile migration. Geophysics , 2008, 73(6): S219-S227. DOI:10.1190/1.2976776 |
| [39] | 何兵寿, 张会星, 魏修成, 等. 双程声波方程叠前逆时深度偏移的成像条件. 石油地球物理勘探 , 2010, 45(2): 237–243. He B S, Zhang H X, Wei X C, et al. Imaging conditions for two-way acoustic wave equation pre-stack reverse-time depth migration. Oil Geophysical Prospecting (in Chinese) , 2010, 45(2): 237-243. |
 2013, Vol. 56
2013, Vol. 56

