带电粒子的加速在空间等离子体物理的研究中起着非常重要的作用,而激波加速[1]又是带电粒子加速的一种非常重要的机制.20世纪70年代提出的扩散激波加速(DSA)机制[2-6]成功地解释了和激波加速有关的从宇宙线直至太阳高能粒子事件中高能粒子的幂率谱分布[7],因而被认为是激波加速带电粒子的主要机制.在扩散激波加速机制中,带电粒子被激波上下游的波动所散射,因而它们可以多次穿越激波使带电粒子加速到很高的能量.根据扩散激波加速的理论,需要初始注入粒子的能量大于某一阈值[8-12],才能进行激波扩散加速,假如初始注入粒子的能量小于这个阈值,那么将得不到有效的加速.
在准平行激波中,由于被激波反射的上游带电粒子可沿磁场向上游移动很长的距离,从而在上游形成束流不稳定性并激发等离子体波动[13],进而这些波动可散射带电粒子使它们来回多次穿过激波.因此,即使初始注入粒子的能量很小,在准平行激波中也可通过激波扩散加速机制被加速到很高的能量.但是,在准垂直激波中,被激波反射到上游的带电粒子不可能向激波的上游运动很长的距离,也就不可能在激波上游激发等离子体波动.因此,初始注入粒子需要较高的能量才能在准垂直激波中通过扩散激波加速机制加速.或者说,带电粒子在被扩散激波加速机制加速前,需要某种预加速机制[14]先将带电粒子加速到比较高的能量.一般认为,激波冲浪加速[15]和激波漂移加速[16]提供了准垂直激波中扩散激波加速所需的预加速机制.另外,最近Yang等人的工作[17-19]显示准垂直激波的重构过程可更有效地以激波冲浪加速和激波漂移加速的方式加速带电粒子,给准垂直激波提供更有效的预加速机制.
空间环境中的等离子体往往处于湍动状态,最近的研究[20-21]表明,这种等离子体湍动对带电粒子的散射可能使带电粒子来回多次穿过激波.在准垂直激波中,这些等离子体湍动可使扩散激波加速机制所需的较高初始注入粒子能量大大降低,极大地提高扩散激波加速的效率.本文通过试验粒子方法研究了等离子体湍动对准垂直激波中粒子加速的影响.和以往的采用三维各向同性的湍动模式[22-24]的研究不同的是,我们的研究采用的是组合湍动模式[25-27],并考虑了激波角θBn(激波法向和激波上游磁场夹角)、粒子的初始能量和等离子体湍动的强度等参数对带电粒子在准垂直激波中加速的影响.
2 计算模型
在本文中,我们假定带电粒子对场和激波结构不产生影响,也即通过试验粒子方法研究等离子体湍动对准垂直激波中带电粒子加速的影响.我们在激波坐标系中研究带电粒子的加速,在此坐标系中,激波上游(x<0)的等离子体流动速度为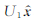

我们可以将激波上下游总磁场表示为B1,2(r)=〈B1,2〉+δB1,2(r),该式右侧第一项为背景磁场,第二项为湍动磁场.激波上游的湍动磁场可表示为[27]
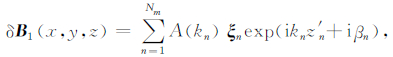
|
(1) |
其中
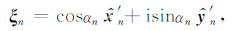
|
(2) |
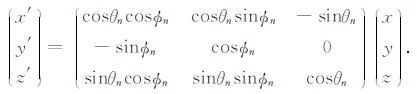
|
(3) |
在(1)式中,A(kn)为波模n的振幅,kn为相应的波数,αn为极化角度,βn为相位,波模的传播方向用θn和ϕn来表示.其中,
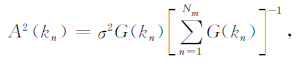
|
(4) |
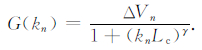
|
(5) |
在(4)式中,σ2为波方差,Lc为相关长度,ΔVn是依赖于湍动维数的归一化因数,γ是依赖于湍动维数的能谱指数.在本文中,我们采用组合模型来拟合等离子体湍动,这种湍动可看成是一维和二维湍动叠加而成的,即δB(x,y,z)=δB1D(z)+δB2D(x,y).令ΔVn=Δkn,γ=5/3和θn=0,就可得到一维湍动;取ΔVn=2πknΔkn,γ=8/3,θn=π/2和αn=π/2,即可得到二维湍动.需要注意的是,激波上下游的湍动磁场满足:δB2x=δB1x,δB2y=rδB1y和δB2z=rδB1z,r为激波的压缩比[22].
在计算中,设置的波模数为300,最小波数为kmin=2π × 10-5Ω1/VA,最大波数为kmax=2πΩ1/VA,其中Ω1=e〈B1〉/m为质子在激波上游背景磁场中的回旋频率,VA为激波上游依赖于上游背景磁场的Alfven速度.采用的组合湍动模型中,一维和二维湍动的强度之比为〈δB1D2〉/〈δB2D2〉=20%:80%.激波的压缩比为4,也即U1/U2=4,Bz2/Bz1=4.激波的厚度取为0.06VA/Ω1,激波面的位形用双曲正切函数拟合,激波上游的等离子体流速为U1=5.47VA.我们通过跟踪12000个质子的轨迹来研究对带电粒子的加速,一开始这些粒子均匀地分布在-1420VA/Ω1<x<-100VA/Ω1的区域内,它们在上游坐标系中满足球壳状速度分布[18],其轨迹可以通过积分下面的方程得到,即
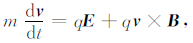
|
(6) |
其中,q是粒子电荷,m是粒子的质量,v为粒子的速度.粒子的位置确定后,我们就可知其对应的电磁场,然后通过Bulirsh-Stoer积分(6)式,得到下一时刻的粒子的位置和速度[31].
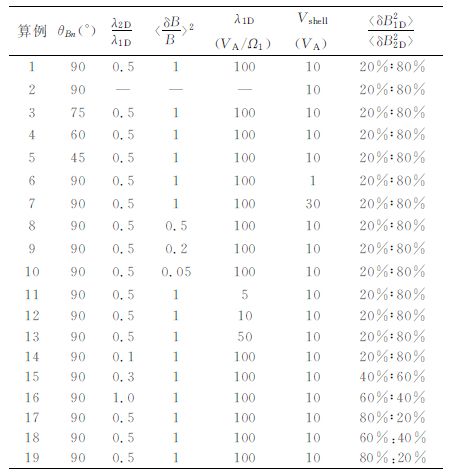
3 计算结果表 1列出了我们计算的19个算例,算例1为一基准算例,其中,θBn=90°,λ2D/λ1D=0.5,〈δB/B〉2=1.0,λ1D=100VA/Ω1,以及粒子球壳状分布的半径为Vshell=10VA,时间步长为Δt=0.05Ω1-1.算例2为不加湍动时的情况,算例3-5,6-7,8-10,11-13,14-16和17-19则分别考虑了θBn,Vshell,〈δB/B〉2,λ1D,λ2D/λ1D和〈δB1D2〉/〈δB2D2〉的影响.除非特别说明,总的模拟时间为1400Ω 1-1.
|
|
表 1 模拟中的参数 Table 1 The parameter of our simulations |
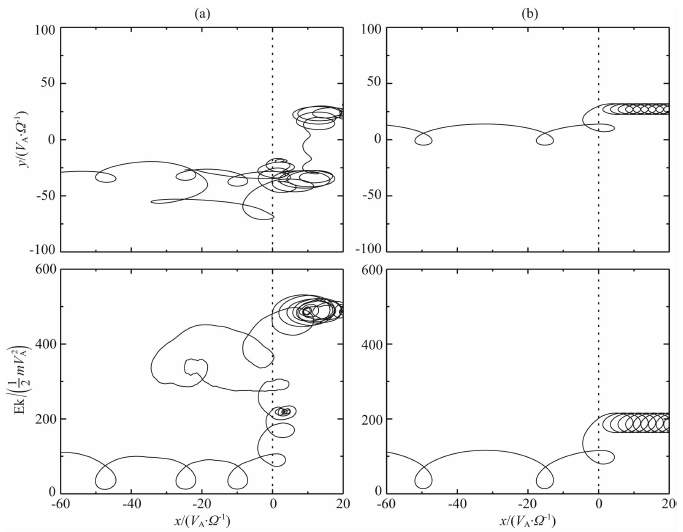
图 1是(a)有湍动和(b)没湍动情况下一个典型粒子的运动轨迹和能量变化.在两种情况下,一开始粒子所在坐标均为(-980.0529816,0.4164738,0.1722941),跟踪(a)中粒子的时间约60Ω1-1,跟踪(b)中粒子的时间约26Ω1-1.从图中可以看出,存在湍动与不存在湍动的情况下粒子的运动有明显区别:在没有湍动的情形下,被激波反射到上游粒子会很快到激波的下游,粒子只能被加速一次,被加速到的能量并不是很高;而在有湍动的情况下,被激波反射的粒子到达下游后会回到上游,并可以被激波反射且加速很多次,最终达到的能量可以很高.其原因在于,在有湍动的情况下,粒子可以横越背景磁场运动,因而到达激波下游的粒子有可能回到激波上游,并被激波加速,而在没有湍动的情况下,粒子很难跨越背景磁场,到达激波下游的粒子一般不能再回到激波的上游.
|
图 1 激波中加湍动(a)与未加湍动(b)的粒子轨迹和能量变化 Fig. 1 Time trajectory and energy gain of particle accelerated at shock waves (a) with turbulence and (b) with no turbulence |
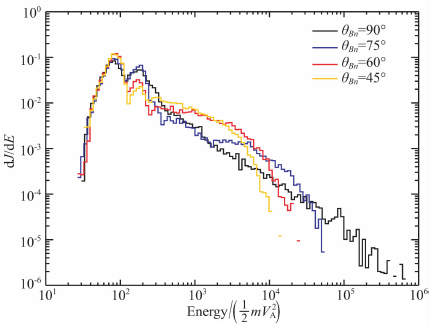
图 2比较了激波角θBn对被激波加速后的粒子能谱的影响,该图对应算例1,3-5.从最终的能谱(图中,J代表通量(flux),E代表能量,dJ/dE表示dE中的粒子通量)可以看出,随着θBn的增大,被加速到高能量的粒子就越多,在能谱图上高能尾也越明显.我们的结果与在激波中加上各向同性湍动的模拟结果一致[24].
|
图 2 不同θBn情况下粒子在激波下游的粒子能谱 Fig. 2 Energy spectra of particles downstream of the shock with different θBn |
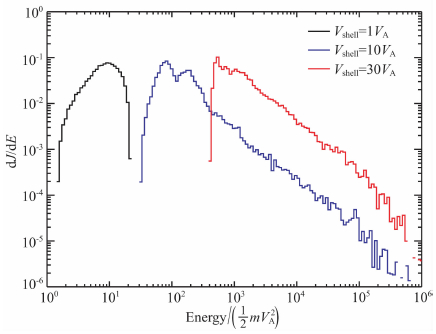
图 3是我们对比不同球壳半径时粒子的加速情况,该图对应算例1,6-7.其中球壳半径为1VA的情况下粒子没有很明显的加速,而其它情况则有较为明显的加速.同时,随着球壳半径的增大,粒子加速所达到的绝对能量逐渐变大,也就是说,初始能量越大的粒子更容易加速到较高的能量.
|
图 3 不同初始能量的粒子在垂直激波下游的能谱 Fig. 3 Energy spectra of particles downstream of the perpendicular shock with different thermal velocity |
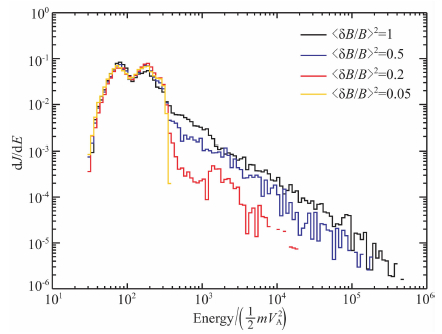
图 4对比了不同强度的湍动情形下粒子的加速情况,对应算例1,8-10.可以看到,随着湍动强度的增大,粒子加速的有效性就越大,这是由于湍动加大,磁场对粒子的横向散射效率就越高,更有利于粒子的加速.但同时也看到,当湍动达到一定比值(〈δB/B〉2)时,继续增大湍动强度,而粒子加速的有效性却没有明显增大.
|
图 4 不同湍动强度情况下粒子在垂直激波下游的能谱 Fig. 4 Energy spectra of particles downstream of the perpendicularshock with the difference in the fluctuating magnetic field energy density |
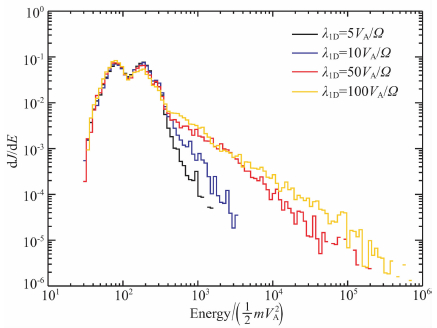
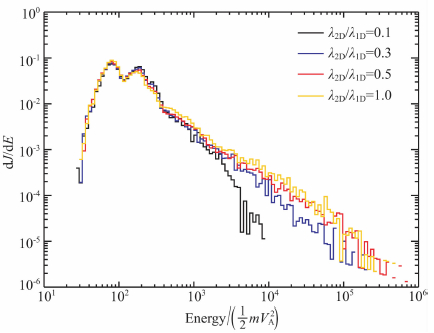
由对应算例1,11-13的图 5中的能谱可知,增大湍动的相关长度,粒子可以更容易地加速到较高能量,相关长度是磁力线偏离背景磁力线的特征距离[32],这一特征距离的增大,即湍动磁力线的曲率半径增大,更有利于粒子穿越激波上下游,从而使粒子得到更为有效的加速.其实图 6(对应算例1、14-16)中能谱随相关长度比(λ2D/λ1D)的变化的本质也正是如此,提高λ2D/λ1D的比值,即增大2D湍动中的相关长度(λ2D),得到了更有效的加速.但当λ2D/λ1D的比值达到一定值时,继续提高λ2D/λ1D的比值并没有提高粒子的加速效率.
|
图 5 不同相关长度情况下粒子在垂直激波下游的能谱 Fig. 5 Energy spectra of particles downstream of the perpendicular shock with various values of coherence length |
|
图 6 对比湍动强度较强情况下不同相关长度比的粒子能谱 Fig. 6 Comparison of the downstream energy spectra with different ratio of the coherence length of the turbulence |
|
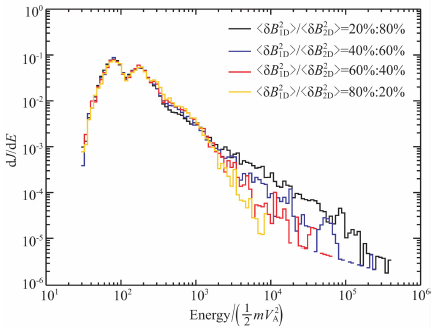
图 7 对比不同一维二维湍动强度比例情况下粒子在激波下游的能谱 Fig. 7 Comparison of the downstream energy spectra with different ratio of strength of 1D turbulence and 2D turbulence |
最后,我们对比了不同的一维二维湍动强度比的情况下,激波对粒子的加速情况,对应算例1,17-19.可以发现,二维湍动强度比例越高,激波对粒子加速的有效性就越大,即二维湍动强度越大,湍动的复杂程度就越高,那么粒子横向散射便会越强,这有利于粒子束缚于激波面附近,从而被更加有效地加速.
4 结论我们利用试验粒子方法研究了存在等离子体湍动情况下准垂直激波对带电粒子的加速,并采用组合模型来拟合等离子体湍动.结果表明:
(1)等离子体湍动的存在使带电粒子可横越背景磁场运动,因而粒子可来回穿过激波并被加速很多次,从而达到很高的能量;
(2)在一段时间内,随着激波角θBn的增加,激波可将带电粒子加速到更高的能量;
(3)初始速度大的粒子更容易被加速到高能量;
(4)在一定的范围内,随着湍动强度的增加,粒子可以得到更为有效的加速;
(5)等离子体湍动相关长度λ2D/λ1D比值的增加,使粒子更容易地被加速到高能量;
(6)在组合湍动中,二维湍动强度比例的增大,可以增强激波对粒子加速的有效性,使粒子更容易加速到较高能量.
通常认为在准垂直激波中,由于很难跨越磁场,带电粒子很难得到多次加速,因而很难加速到很高的能量.本文的研究表明,在存在等离子体湍动的情况下,准垂直激波同样可以多次加速粒子,并将它们加速到很高的能量.空间中,行星际激波加速周围太阳风中的粒子至较高能量,当与地球磁层相互作用时,其携带的一部分高能粒子沿着地球磁场进入地球南北极,且进入极地高层大气,与大气中的原子或分子碰撞并激发,可能形成极光[33-34],即激波加速的太阳风高能粒子也是形成极光的一种可能来源.
| [1] | Jones F C, Ellison D C. The plasma physics of shock acceleration. Space Science Reviews , 1991, 58(1): 259-346. DOI:10.1007/BF01206003 |
| [2] | Axford W I, Leer E, Skadron G. The acceleration of cosmic rays by shock waves.//International Cosmic Ray Conference, 15th, Plovdiv, Bulgaria, 1977. |
| [3] | Bell A R. The acceleration of cosmic rays in shock fronts.I.. Monthly Notices of the Royal Astronomical Society , 1978, 182: 147-156. DOI:10.1093/mnras/182.2.147 |
| [4] | Bell A R. The acceleration of cosmic rays in shock fronts.II.. Monthly Notices of the Royal Astronomical Society , 1978, 182: 443-455. DOI:10.1093/mnras/182.3.443 |
| [5] | Blandford R D, Ostriker J P. Particle acceleration by astrophysical shocks. The Astrophysical Journal , 1978, 221: L29-L32. DOI:10.1086/182658 |
| [6] | Krymskii G F. A regular mechanism for the acceleration of charged particles on the front of a shock wave. Akademiia Nauk SSSR Doklady , 1977: 1306-1308. |
| [7] | Blandford R, Eichler D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Physics Reports , 1987, 154(1): 1-75. DOI:10.1016/0370-1573(87)90134-7 |
| [8] | Ellison D C. Monte Carlo simulation of charged particles upstream of the Earth's bow shock. Geophys. Res. Lett. , 1981, 8(9): 991-994. DOI:10.1029/GL008i009p00991 |
| [9] | Quest K B. Theory and simulation of collisionless parallel shocks. J. Geophys. Res. , 1988, 93(A9): 9649-9680. DOI:10.1029/JA093iA09p09649 |
| [10] | Scholer M. Diffuse ions at a quasi-parallel collisionless shock: Simulations. Geophys. Res. Lett. , 1990, 17(11): 1821-1824. DOI:10.1029/GL017i011p01821 |
| [11] | Giacalone J, Burgess D, Schwartz S J, et al. Hybrid simulations of protons strongly accelerated by a parallel collisionless shock. Geophys. Res. Lett. , 1992, 19(5): 433-436. DOI:10.1029/92GL00379 |
| [12] | Kucharek H, Scholer M. Injection and acceleration of interstellar pickup ions at the heliospheric termination shock. J. Geophys. Res. , 1995, 100(A2): 1745-1754. DOI:10.1029/94JA02559 |
| [13] | Tsurutani B T, Smith E J, Jones D E. Waves observed upstream of interplanetary shocks. J. Geophys. Res. , 1983, 88(A7): 5645-5656. DOI:10.1029/JA088iA07p05645 |
| [14] | Zank G P, Pauls H L, Cairns I H, et al. Interstellar pickup ions and quasi-perpendicular shocks: Implications for the termination shock and interplanetary shocks. J. Geophys. Res. , 1996, 101(A1): 457-477. DOI:10.1029/95JA02860 |
| [15] | Shapiro V D, Üçer D. Shock surfing acceleration. Planetary and Space Science , 2003, 51(11): 665-680. DOI:10.1016/S0032-0633(03)00102-8 |
| [16] | Lever E L, Quest K B, Shapiro V D. Shock surfing vs. shock drift acceleration. Geophys. Res. Lett. , 2001, 28(7): 1367-1370. DOI:10.1029/2000GL012516 |
| [17] | 杨忠炜, 陆全明, 郭俊, 等. 垂直无碰撞激波的离子加速机制. 地球物理学报 , 2008, 51(4): 953–959. Yang Z W, Lu Q M, Guo J, et al. Mechanism of ion acceleration at perpendicular collisionless shocks. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 953-959. |
| [18] | Yang Z W, Lu Q M, Lembège B, et al. Shock front nonstationarity and ion acceleration in supercritical perpendicular shocks. J. Geophys. Res. , 2009, 114(A3): A3111. |
| [19] | Yang Z W, Lembège B, Lu Q M. Impact of the rippling of a perpendicular shock front on ion dynamics. J. Geophys. Res. , 2012, 117(A7): A7222. |
| [20] | Decker R B. The role of magnetic loops in particle acceleration at nearly perpendicular shocks. J. Geophys. Res. , 1993, 98(A1): 33-46. DOI:10.1029/92JA01841 |
| [21] | Guo F, Giacalone J. The effect of large-scale magnetic turbulence on the acceleration of electrons by perpendicular collisionless shocks. The Astrophysical Journal , 2010, 715(1): 406. DOI:10.1088/0004-637X/715/1/406 |
| [22] | Giacalone J, Jokipii J R. Perpendicular transport in shock acceleration. J. Geophys. Res. , 1996, 101(A5): 11095-11106. DOI:10.1029/96JA00394 |
| [23] | Giacalone J, Ellison D C. Three-dimensional numerical simulations of particle injection and acceleration at quasi-perpendicular shocks. J. Geophys. Res. , 2000, 105(A6): 12541-12556. DOI:10.1029/1999JA000018 |
| [24] | Giacalone J. Particle acceleration at shocks moving through an irregular magnetic field. The Astrophysical Journal , 2008, 624(2): 765-772. |
| [25] | Bieber J W, Wanner W, Matthaeus W H. Dominant two-dimensional solar wind turbulence with implications for cosmic ray transport. J. Geophys. Res. , 1996, 101(A2): 2511-2522. DOI:10.1029/95JA02588 |
| [26] | Gray P C, Pontius D H J, Matthaeus W H. Scaling of field-line random walk in model solar wind fluctuations. Geophys. Res. Lett. , 1996, 23(9): 965-968. DOI:10.1029/96GL00769 |
| [27] | Giacalone J, Jokipii J R. The transport of cosmic rays across a turbulent magnetic field. The Astrophysical Journal , 1999, 520(1): 204-214. DOI:10.1086/apj.1999.520.issue-1 |
| [28] | Giacalone J, Armstrong T P, Decker R B. Effect of magnetic overshoot on shock drift acceleration. J. Geophys. Res. , 1991, 96(A3): 3621-3626. DOI:10.1029/90JA01627 |
| [29] | Lee M A, Shapiro V D, Sagdeev R Z. Pickup ion energization by shock surfing. J. Geophys. Res. , 1996, 101(A3): 4777-4789. DOI:10.1029/95JA03570 |
| [30] | Gosling J T, Winske D, Thomsen M F. Noncoplanar magnetic fields at collisionless shocks: A test of a new approach. J. Geophys. Res. , 1988, 93(A4): 2735-2740. DOI:10.1029/JA093iA04p02735 |
| [31] | Decker R B. Computer modeling of test particle acceleration at oblique shocks. Space Science Reviews , 1988, 48(3-4): 195-262. |
| [32] | Li G, Shalchi A, Ao X, et al. Particle acceleration and transport at an oblique CME-driven shock. Advances in Space Research , 2012, 49(6): 1067-1075. DOI:10.1016/j.asr.2011.12.027 |
| [33] | Craven J D, Frank L A, Russell C T, et al. Global auroral responses to magnetospheric compressions by shocks in the solar wind: Two cases studies.//Solar Wind-Magnetosphere Coupling, Proceedings of the Chapman Conference. Pasadena: Tokyo/Dordrecht, Terra Scientific Publishing, 1986: 367-380. |
| [34] | Du A M, Sun W, Tsurutani B T, et al. Observations of dawn-dusk aligned polar cap aurora during the substorms of January 21, 2005. Planetary and Space Science , 2011, 59(13): 1551-1558. DOI:10.1016/j.pss.2011.06.021 |
 2013, Vol. 56
2013, Vol. 56