地层横波慢度信息对石油勘探开发有着重要的意义,它与地层岩石性质密切相关.井壁周围地层性质常常因为井壁应力集中、钻井机械损坏和泥浆入侵等外力因素发生变化,进而导致井壁周围地层出现横波慢度的径向变化带.反之,如果已知径向变化带横波慢度分布情况,就可以了解井壁周围地层性质的改变.对于慢地层(地层横波慢度大于井孔流体纵波慢度),传统的单极子仪器探测不到横波首波,原因是井外地层的横波慢度大于井孔流体纵波慢度时,全波列中无法探测到横波首波信号.因此,人们通常采用偶极弯曲波来反演地层横波的信息[1-2].
1996-2006年Sinha等发展了基于微扰法[3]和BG理论[4]的反演算法[5-8],来反演地层横波慢度的径向分布,在处理实际数据时,此方法不能同时满足高分辨率和高精度需求.2000年,Braunisch等又提出一种利用多频、多模式波的信息联合反演地层横波慢度的方法[9],但此方法在慢地层应用受限. 2010年,Tang等建立了参量化的、高频约束条件下的反演方程[10],方程假定地层横波慢度是径向半径r的指数函数,并且在反演的过程中对弯曲波进行高频约束,但高频弯曲波的激发强度较小,易受噪声等的干扰,为反演结果的准确性带来了挑战.2011-2012年,Yang等建立了套管井模型下的参量化的反演方程[11-12],他们也假定地层横波慢度是径向半径r的指数函数,指数函数的变化形式由3个参数控制,反演地层横波慢度的径向分布,转换为对这3个参数的反演,但是反演计算方法的收敛性受初始值影响严重.
另外,国内的陈雪莲和王瑞甲研究了TI地层模式波对井孔流体参数和地层参数的灵敏度,分析了各模式波的径向探测深度,其中弯曲波探测深度约为4个井孔半径[13].这也说明可通过弯曲波来获取井壁周围地层的横波慢度,进而了解地层的性质.
前人的工作都说明了,利用弯曲波频散可以求解井壁周围地层横波慢度的径向分布,进而了解井壁周围的地层性质.但是,前人对所采用的反演方法的特性分析较少,并很少涉及如何提高计算效率.本文的工作则主要侧重于这两个方面.本文在前人的工作基础上,首先计算了地层横波慢度径向均匀(以下简称均匀模型)和非均匀情况下(以下简称非均匀模型,非均匀模型的产生是由于均匀模型的横波慢度在径向上发生了变化)的时域全波列波形.其次利用频域方法[14]提取了波形的弯曲波频散曲线,并对弯曲波频散曲线进行了拟合校正[15].再次,讨论了如何结合微扰法与BG理论,基于非均匀模型和均匀模型之间弯曲波的差异,进行地层横波慢度径向分布的反演计算.最后,我们分析了如何在反演的迭代过程中提高计算效率,并且用多种计算实例,验证了所采用的反演算法的鲁棒性,为它的现场应用打下基础.
2 偶极井孔声场理论在三维柱坐标系(r,θ,z)下,以偶极源的中心为原点,并使z轴与井轴方向一致.根据文献[16],井孔内位移势函数φf在频率波数内的稳态声场表达式如下:
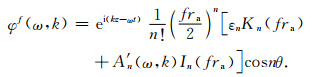
|
(1) |
井外地层声场纵波位移势函数,SH横波位移势函数和SV横波位移势函数在频率波数内的稳态声场表达式如式:

|
(2) |
其中,n=1代表偶极源,ra为偶极距,r为径向半径,εn=2,ω为角频率,In和Kn为n阶虚宗量贝塞尔函数,A
′n、An、Bn、Cn、Dn、En和Fn是待定系数,由井壁处的边界条件确定.
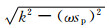

在相邻2个层的界面上声场应满足边界条件.如果在半径rj(下标j=0,…,N表示径向上的层的序号,N表示径向上的层数)处的界面两侧都是固体,在界面上胶结良好,则界面上的位移和应力分量应该连续,即
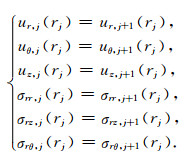
|
(3) |
式中,ur为法向位移分量,uθ和uz为切向位移分量,σrr为法向应力分量,σrz和σrθ为切向应力分量.
在井壁r0处,其界面的内侧是液体,外侧是固体,此时边界条件变成法向位移ur和法向应力σrr连续,切向应力σrz和σrθ为零,切向位移分量uθ和uz无需考虑,即
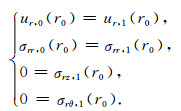
|
(4) |
层与层之间的声场由汤姆森-哈斯克(Thomson-Hanskell)传播矩阵[17]来连接,反复利用各层介质的传递矩阵和边界条件,就可以得求的径向分层地层的声场.对于偶极声源,测量的是径向位移,是瞬态声场,需要考虑声源的影响,其在空间-时间域的具体表达式为[16]
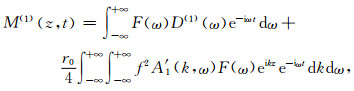
|
(5) |
式中,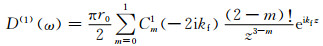
计算分析时,本文给出了两个模型,模型1的井外是无限大均匀地层,模型2的井外地层横波慢度径向分层,它是由模型1的地层横波慢度径向扰动所致.两个模型的井孔半径r0=0.1m,井孔流体密度ρf=1000kg/m3,井孔流体纵波慢度sf=666.7μs/m.模型1的地层参数见表 1,模型2中,地层横波慢度径向是非均匀的,导致剪切模型模量径向非均匀,进而引起纵波慢度径向非均匀,然而纵波慢度对弯曲波频散影响很小[3],所以为了提高计算效率,计算过程中假设模型2的地层纵波慢度与模型1相同,此外,地层密度对弯曲波频散影响也很小,在计算时也同样假设模型2的地层密度与模型1相同,模型2中地层横波慢度ss的径向分布数值见表 2.图 1为模型2的示意图,其中径向半径b和井壁r0之间为横波慢度的变化带,b=0.3m.
|
|
表 1 地层参数 Table 1 Parameters of formation |
|
|
表 2 变化带横波慢度值 Table 2 The values of shear wave slowness of altered zone |

|
图 1 井孔与地层模型 Fig. 1 The model of borehole and formation |
文中计算用到的声源函数为F(ω)=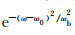
图 2中黑色和红色曲线分别表示模型1和模型2的偶极全波波列,从图 2可以看出模型2的全波波列明显延后于模型1的全波波列,这是由于模型2的井壁周围地层横波慢度增加所致.

|
图 2 偶极子全波列波形图,模型1(黑色)和模型2(红色) Fig. 2 Dipole waveforms of model one (black) and model two (red) |
在图 2的全波列中,占主要地位的是弯曲波成分.为了分析弯曲波的频散特征,可以采用频域法从时域波形中提取各频率下弯曲波的慢度.本文利用频域加权相似法对图 2中两个模型的全波波列进行处理,提取了偶极全波波列的弯曲波.
图 3a中黑色和红色曲线分别表示模型1和模型2中第一道波列的频谱.图 3b中,黑色和红色圆圈状曲线分别为对模型1和模型2的波列提取的弯曲波频散,对它们利用正切(或反正切)函数进行拟合,分别得到图中黑色和红色实线,利用频散方程[19]计算两个模型的弯曲波频散见三角状曲线,这三种方法求解的频散吻合性较好.拟合的好处是可以得到宽频带范围内的弯曲波,有效地消除了频散曲线中异常数据点对反演结果的影响,提高了反演计算的准确性.此外,从图 3b中可以看出频率在1kHz以下时,红色和黑色实线几乎重合,并且随着频率向低频移动,二者的弯曲波慢度都趋向于模型1中地层横波慢度,这也就帮助确定发生径向变化前地层横波慢度的数值,在反演计算过程中,此数值为参考模型的地层横波慢度.

|
图 3 (a)两个模型的第一道波列的频谱,(b)两种模型的弯曲波频散:提取(圆圈状)、拟合(线状)和利用频散方程计算(三角形) Fig. 3 (a) The first spectrum of each model; (b) Flexural dispersion curves of each model:the extractive ones (circle), the fitted ones (line) and the calculated ones (triangle) based on dispersion equation |
由图 2和图 3可以看出,地层横波慢度在径向上的变化分布影响了偶极子弯曲波传播特征,因此弯曲波传播特征的改变可以被用来确定地层横波慢度在径向上的变化情况,也即地层性质的改变.
本文选择的反演方法结合了微扰法和BG理论,根据此反演方法,待求模型的井外有一个横波慢度的径向变化带,此变化带是由于参考模型(参考模型的井外是无限大均匀地层)的横波慢度在近井壁处发生径向扰动所致.处理待求模型的偶极全波波列得到的弯曲波慢度在低频处的趋近值,可以认为是参考模型的地层横波慢度srefer.利用牛顿-拉夫森(Newton-Raphson)方法[20]计算频散方程:

|
(6) |
可以求解出参考模型的弯曲波频散vrefer=ω/k,进而求解出扰动部分贡献的弯曲波频散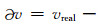
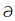
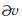
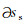
在柱坐标系下,根据微扰法,当参考模型空间中有扰动发生后,扰动后的模型的弯曲波相速度也相应的发生了改变:
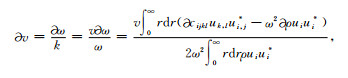
|
(7) |
其中,v为参考模型的相速度,
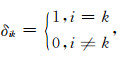
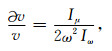
|
(8) |
其中,
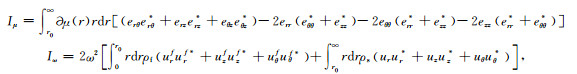
|
因此只要已知没有扰动时参考模型的相速度,就可求解发生扰动后的模型的相速度:
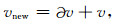
|
(9) |
因此根据方程(9),当地层横波慢度从井壁r0处到径向半径b处,发生了扰动可以计算地层横波慢度从井壁r0处到b发生径向扰动后的弯曲波频散,只是这里的积分区域变成了r0到b,即
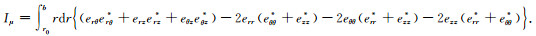
|
Backus和Gilbert提出由于反问题解的非唯一性,不去求反问题解本身而去求它的某种平均乃是消除反问题非唯一性的一种途径,这种平均称为解估计.这里结合微扰法和BG理论,给出了利用弯曲波频散求解地层横波慢度的主要公式.
假设已知在频率点ωi处(i=1,…,N),弯曲波相速度的相对变化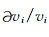
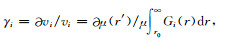
|
(10) |
其中Gi(r)为核函数,μ=ρs/ss2是扰动发生前的地层剪切模量.ρs、ss、i、N和r′分别表示井外地层密度、参考模型横波慢度、选择的频率点编号、总频率点数和地层剪切模量(横波慢度)发生变化的径向的位置.(10)式揭示的正演问题是:已知∂μ(r ′)/μ来求解∂vi/vi;反演问题是:已知∂vi/vi来求解∂μ(r′)/μ.
利用方程(8)对(10)进行整理求解出核函数:
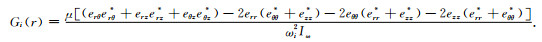
|
(11) |
根据BG理论,在反演∂μ(r
′)/μ时,不去求解∂μ(r′)/μ本身,而是求解∂μ(r′)/μ的估计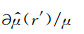
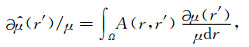
|
(12) |
其中:A(r,r ′)为平均核函数,且:
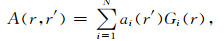
|
(13) |
则根据(10)-(13)式有:
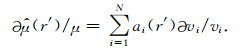
|
(14) |
因此只要求解出待定系数组{ai}i=1,…,N,就能计算出r ′处的剪切模量的相对变化的估计. Backus和Gilbert的研究给出了系数组的一系列准则和方法,具体的过程见参考文献[5].
下面介绍如何提高所采用的结合微扰法和BG理论的反演方法的计算效率,这也是本文的重点.
根据BG理论,正确评价解估计的准则是在展布函数和方差之间取合理的折衷.Backus和Gilbert建议采用以下目标函数:
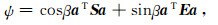
|
(15) |
其中,aTSa是平均核函数A(r,r ′)的展布函数,aT Ea是解估计的方差,β为折衷参数且β∈(0,π/2).
求解方程(15)的过程是个对β不断寻优的过程,采用传统的迭代方式,计算效率较低,本文采用了1995年杨文采提出的改进措施[21].在迭代开始时,先求低分辨率小方差的解估计,随非线性迭代逐步提高分辨率.具体地,在开始时取折衷因子β0=π/2,随迭代逐步减小.即:

|
(16) |
迭代次数q增加时,βq减小,这样的选取方式避免了内循环中解线性方程组的无谓计算,大大降低了计算成本.
3.3 反演流程结合微扰法与BG理论,利用弯曲波频散反演地层横波慢度径向分布的基本流程可以归纳为:
(1)井孔半径、井孔流体参数和地层参数(除横波慢度外)已知,从波形数据中提取弯曲波频散vreal,对其进行拟合得到了宽频带范围的弯曲波慢度,其在低频处趋近的数值即为参考模型的横波慢度;
(2)对于选定的参考模型,计算偶极频散方程,得到参考模型的弯曲波频散vrefer;
(3)比较vreal与vrefer,若二者之间的差别小于某一小值min,则认为地层横波慢度没有发生径向扰动,否则认为地层横波慢度相对参考模型发生了径向扰动,则开始反演计算:
首先计算核函数(10)式,其次联合(10)-(15)式计算出待定系数组{ai},i=1,2,…,N,则得到了径向半径r ′处的地层横波慢度的解估计:

|
(17) |
改变r ′值就可得到井外地层横波慢度的径向分布,它与地层横波慢度真实值之间相对误差为:
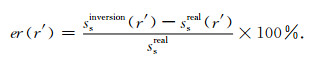
|
(18) |
本文假设模型2的偶极全波列为实际测得数据.为了分析结合微扰法和BG理论反演方法的特性,本文对偶极全波列存在以下5种情况时的数据进行了处理,得到了各情况下地层横波慢度的径向分布.这5种情况是:(1)无噪声和参数误差;(2)井孔流体慢度sf存在10%以内误差;(3)井外地层纵波慢度sp存在10%以内误差;(4)全波波列存在SNR=20dB的噪声;(5)全波波列存在SNR=10dB的噪声.
4.1 无噪声和参数误差假设图 2中的红色波列数据已知,其所对应的模型井外地层横波慢度径向分布情况未知.根据第2章介绍的反演方法,得到的参考模型的弯曲波频散见图 4a中黑色曲线,处理图 2中的红色波列得到的未知模型的弯曲波频散见图 4a中红色曲线.本文选择6个频率点下两个模型的弯曲波慢度之差作为反演计算的输入参数,相邻点之间频率间隔为Δf=1.0kHz,每个频率点下两个模型的弯曲波慢度用直线连接,见图中圆圈所标示.
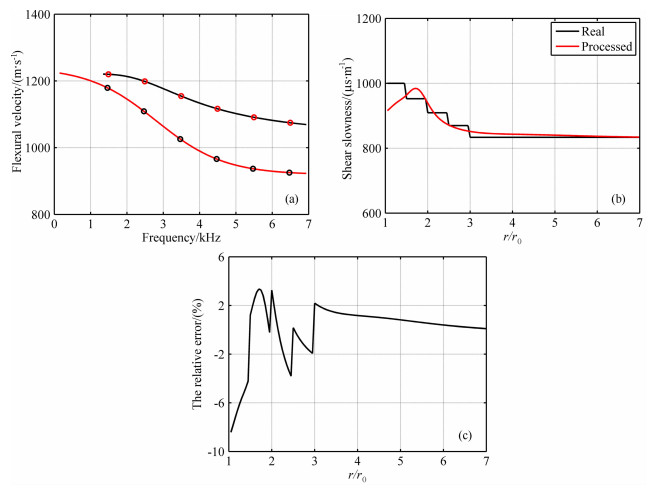
|
图 4 (a)反演所用的不同频率点的待求模型(红色)和参考模型(黑色)的弯曲波相速度;(b)反演的(红色)和实际的(黑色)地层横波慢度径向分布;(c)反演的与实际的地层横波慢度之间相对误差的径向分布 Fig. 4 (a) Flexural wave velocities of objective model (red) and reference model (black) in different frequencies; (b) Inverted (red) and actual (black) radial profiles of shear wave slowness; (c) Radial profile of relative error between inverted and actual shear wave slowness |
图 4b中红色曲线为反演计算得到的地层横波慢度的径向分布,黑色阶梯状曲线为地层横波慢度真实的径向分布.反演结果相对误差的径向分布见图 4c,从图中可以看到反演结果相对误差基本控制在10%以内,并且离井壁越近,误差相对越大.
4.2 其他参数存在误差实际数据比理论数据要更复杂,可能导致获取的其他地层参数或者井孔参数不准确,为此,我们还分析了这些参数存在误差时对反演结果的影响.本文首先研究了井孔流体慢度sf分别存在-10%、-5%、5%和10%的误差时对反演结果的影响.反演的与实际的地层横波慢度的径向分布见图 5a,反演结果的相对误差的径向分布见图 5b.我们注意到,sf存在误差与sf无误差的反演结果保持了很好的一致性.
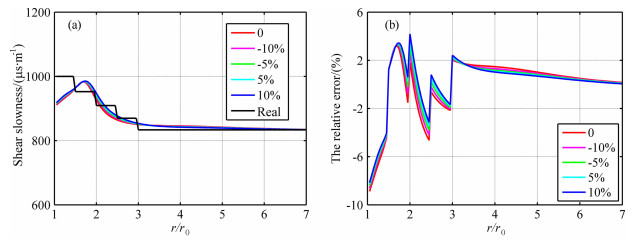
|
图 5 sf无误差与sf分别存在-10%,-5%、5%、10%的相对误差时:(a)反演的与实际的地层横波慢度的径向分布;(b)反演的与实际的地层横波慢度之间相对误差的径向分布 Fig. 5 When there is no, -10%, -5%, 5% or 10% relative error ofsf:(a) inverted and actual radial profiles of shear wave slowness, (b) radial profile of relative error between inverted and actual shear wave slowness |
其次研究了井外地层纵波慢度sp分别存在-10%、-5%、5%和10%的误差时对反演结果的影响.反演的与实际的地层横波慢度的径向分布见图 6a,反演结果的相对误差的径向分布见图 6b.我们注意到,sp存在误差与sp无误差的反演结果也保持了很好的一致性,这也是计算时假设地层纵波慢度为一固定值的原因.
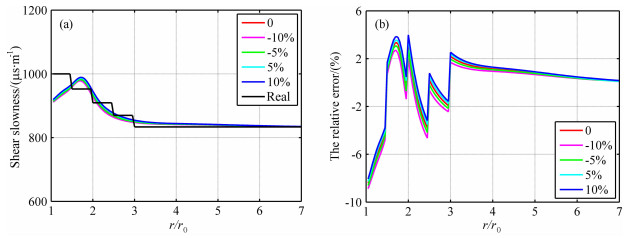
|
图 6 sp无误差与sp分别存在-10%,-5%、5%、10%的相对误差时:(a)反演的与实际的地层横波慢度的径向分布,(b)反演的与实际的地层横波慢度之间相对误差的径向分布 Fig. 6 When there is no, -10%, -5%, 5% or 10% relative error ofsp:(a) inverted and actual radial profiles of shear wave slowness, (b) radial profile of relative error between inverted and actual shear wave slowness |
实际数据中往往存在噪声,为此还应针对波列数据存在噪声的情况做进一步的分析.这部分的工作是通过对图 2中的红色波列分别添加SNR=20dB和SNR=10dB的高斯白噪声各4次来展开的.
图 7显示了分别添加了一次SNR=20dB和SNR=10dB的高斯白噪声后的波形曲线和频谱曲线.图 7a中黑色、红色和蓝色曲线分别表示:无噪声时、存在SNR=20dB和SNR=10dB的噪声时的偶极全波列波形;图 7b的曲线为相应的第一道波形,图 7c为相应的第一道波形的频谱(图中标示了噪声的大小),图 7d为SNR=20dB时八道波列的频谱,图 7e为SNR=10dB时八道波列的频谱.从图 7a和7b看到噪声对波形的影响似乎不太明显,但是从图 7c-7e看到,噪声的存在使得低频和高频处频谱相关性较差,进而导致提取的弯曲波在这些频段范围内出现异常点,这也是对提取的弯曲波进行拟合的主要原因.
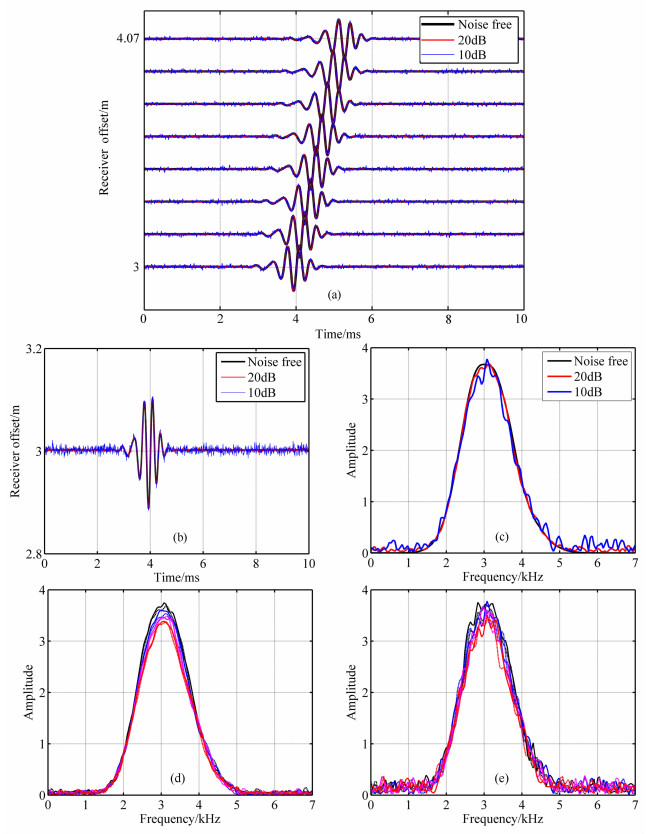
|
图 7 (a)偶极全波列波形;(b)第一道波列;(c)第一道波列的频谱;(d)SNR=20dB时八道波列的频谱;(e)SNR=10dB时八道波列的频谱 Fig. 7 (a) Dipole full waveforms; (b) The first waveform of each case; (c) The first spectrum of each case; (d) Eight spectrums when SNR=20dB; (e) Eight spectrums when SNR=10dB |
对图 2中的红色波列加入4次SNR=20dB高斯白噪声后提取的弯曲波频散见8(a-d)中圈状曲线,加入4次SNR=10dB高斯白噪声后提取的弯曲波频散见9a-9d中圈状曲线,8幅图中的实线为对相应圈状曲线的拟合.从这8幅图中可以看到:拟合前低频和高频段的弯曲波频散数据存在异常点,可利用的只有中间频率段的数据,这会导致反演结果的准确性大大降低.拟合后的弯曲波频带范围变宽,可利用的弯曲波数据增加,进而降低了噪声的干扰.加入4次SNR=20dB噪声后反演的与实际的地层横波慢度的径向分布见图 8e,反演结果相对误差的径向分布见图 8f.加入4次SNR=10dB噪声后反演的与实际的地层横波慢度的径向分布见图 9e,反演结果相对误差的径向分布见图 9f.从图 8f和9f可见:存在SNR=20dB和SNR=10dB噪声时,相对误差也基本控制在10%以内,并且与没有噪声情况下的误差吻合度较高,这说明采用的反演方法对噪声不敏感.
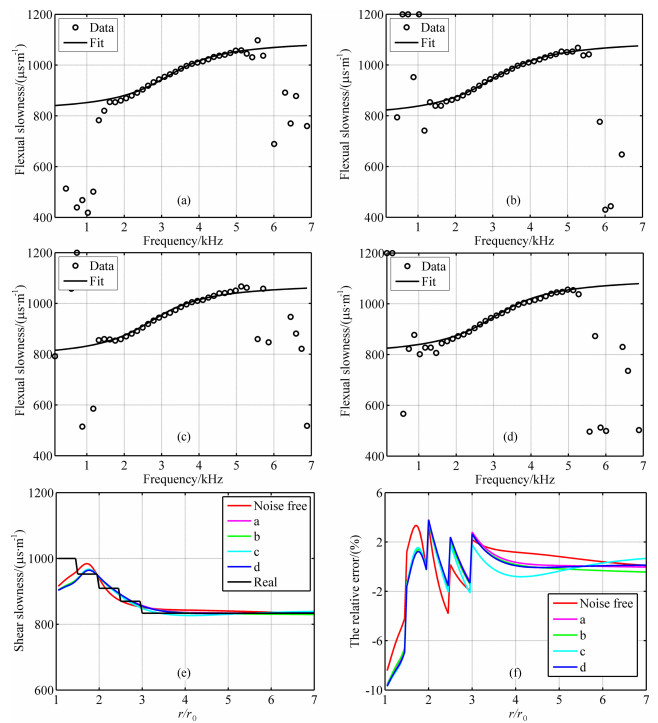
|
图 8 (a-d)SNR=20dB时提取(圈状)和拟合(线状)的弯曲波频散;(e)反演的与实际的地层横波慢度的径向分布;(f)反演的与实际的地层横波慢度之间相对误差的径向分布 Fig. 8 (a-d) Extractive (circle) and fitted (line) flexural dispersion curves when SNR=20dB; (e) Inverted and actual radial profiles of shear wave slowness; (f) Radial profile of relative error between inverted and actual shear wave slowness |
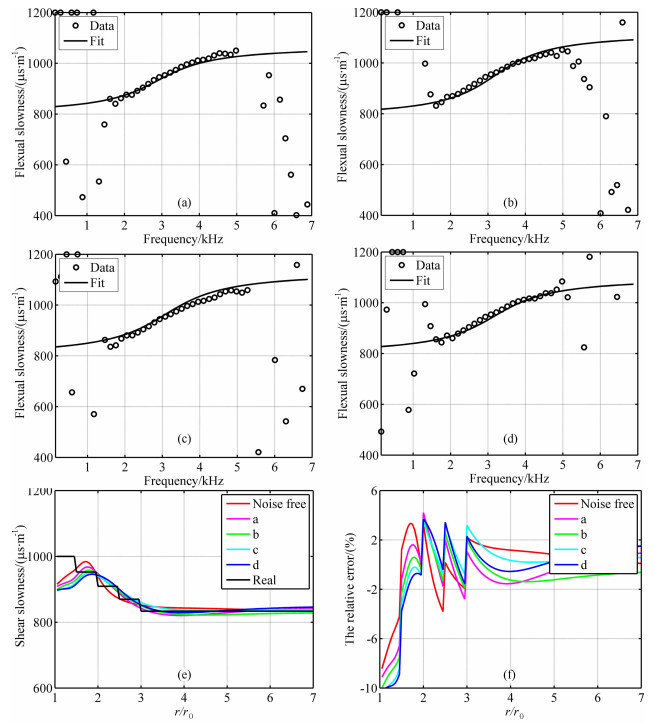
|
图 9 (a-d)SNR=10dB时提取(圈状)和拟合(线状)的弯曲波频散;(e)反演的与实际的地层横波慢度的径向分布;(f)反演的与实际的地层横波慢度之间相对误差的径向分布 Fig. 9 (a-d) Extractive (circle) and fitted (line) flexural dispersion curves when SNR=20 dB; (e) Inverted and actual radial profiles of shear wave slowness; (f) Radial profile of relative error between inverted and actual shear wave slowness |
本文以井外地层横波慢度径向分层模型为例,计算了模型的偶极全波波列,提取了模型的弯曲波频散,利用此弯曲波慢度与井外地层均匀时弯曲波慢度在多频率点下的差异,采用结合微扰法和BG理论的反演方法,得到了径向分层模型井外地层横波慢度的径向分布,并且讨论了如何提高反演计算的效率,以适应现场对数据处理速度的要求.
此外,为了分析采用的反演方法的特性,本文分别对以下5种情况的偶极全波波列数据进行处理,得到了各情况下地层横波慢度的径向分布.这5种情况是:(1)无噪声和参数误差时;(2)井孔流体慢度sf存在10%以内误差时;(3)井外地层纵波慢度sp存在10%以内误差时;(4)全波波列存在SNR=20dB的噪声时;(5)全波波列存在SNR=10dB的噪声时.结果表明:(2)和(3)的反演结果与(1)的反演结果保持了很好的一致性,这是因为sf和sp对弯曲波的影响较小的缘故;在(4)和(5)两种情况下,通过对提取的弯曲波频散进行拟合,得到了较宽频带范围内的弯曲波数据,有效地消除了频散曲线中异常数据点对反演结果的影响,使得(4)和(5)的反演结果相对于(1)的反演结果都没有发生明显的改变,这说明采用的反演方法对噪声不敏感.
以上反演结果都证实了,结合微扰法和BG理论的反演方法具有很好的鲁棒性,可以被用于反演井壁周围地层横波慢度的径向分布,进而了解井壁周围地层的性质.
| [1] | Schmitt D P. Shear wave logging in elastic formations. Journal of the Acoustical Society of America , 1988, 84(6): 2215-2229. DOI:10.1121/1.397015 |
| [2] | Winbow G A. A theoretical study of acoustic S-wave and P-wave velocity logging with conventional and dipole sources in soft formations. Geophysics , 1988, 53(10): 1334-1342. DOI:10.1190/1.1442411 |
| [3] | Ellefsen K J, Cheng C H, ToksÖz M N. Applications of perturbation theory to acoustic logging. Journal of Geophysical Research , 1991, 96(B1): 537-549. DOI:10.1029/90JB02013 |
| [4] | Backus G, Gilbert F. Uniqueness in the inversion of inaccurate gross earth data. Philosophical Transactions of the Royal Society A: Mathematical.. Physical and Engineering Sciences , 1970, 266(1173): 123-192. DOI:10.1098/rsta.1970.0005 |
| [5] | Burridge R, Sinha B K. Inversion for formation shear modulus and radial depth of investigation using borehole flexural waves. SEG Expanded Abstracts , 1996, 158. |
| [6] | Sinha B K, Burridge R. Radial profiling of formation shear velocity from borehole flexural dispersions. IEEE Ultrasonics Symposium Proceedings , 2001, 391. |
| [7] | Sinha B K, Asvadurov S. Dispersion and radial depth of investigation of borehole modes. Geophysical Prospecting , 2004, 52(4): 271-286. DOI:10.1111/gpr.2004.52.issue-4 |
| [8] | Sinha B K, Vissapragada B, Renlie L, et al. Radial profiling of the three formation shear moduli and its application to well completions. Geophysics , 2006, 71(6): E65-E77. DOI:10.1190/1.2335879 |
| [9] | Braunisch H, Habashy T M, Sinha B K, et al. Inversion of borehole dispersions for formation elastic moduli. IEEE Ultrasonics Symposium , 2000, 551. |
| [10] | Tang X M, Patterson D J. Mapping formation radial shear-wave velocity variation by a constrained inversion of borehole flexural-wave dispersion data. Geophysics , 2010, 75(6): E183-E190. DOI:10.1190/1.3502664 |
| [11] | Yang J, Sinha B K, Habashy T M. A Parameterized-model-based radial profiling for formation shear slowness in cased boreholes. SEG San Antonio 2011 Annual Meeting , 2011, 449. |
| [12] | Yang J Q, Sinha B K, Habashy T M. A theoretical study on formation shear radial profiling in well-bonded cased boreholes using sonic dispersion data based on a parameterized perturbation model. Geophysics , 2012, 77(3): WA197-WA210. DOI:10.1190/geo2011-0279.1 |
| [13] | 陈雪莲, 王瑞甲. 横向各向同性弹性地层井孔中模式波的探测深度. 吉林大学学报(地球科学版) , 2008, 38(3): 502–507. Chen X L, Wang R J. Investigating depth of mode waves in the borehole surrounded by transversely isotropic elastic formation. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2008, 38(3): 502-507. |
| [14] | Nolte B, Huang X J. Dispersion analysis of split flexural waves: Borehole acoustics and logging and reservoir delineation consortia annual report. Massachusetts Institute of Technology , 1997. |
| [15] | Tang X M, Li C, Patterson D J. A curve-fitting technique for determining dispersion characteristics of guided elastic waves. Geophysics , 2010, 75(3): E153-E160. DOI:10.1190/1.3420736 |
| [16] | Paillet F L, Cheng C H. Acoustic waves in boreholes. Boca Raton/Ann Arbor/Boston London: CRC Press, 1991 . |
| [17] | Schmitt D P. Effects of radial layering when logging in saturated porous formations. Journal of the Acoustical Society of America , 1988, 84(6): 2200-2214. DOI:10.1121/1.397067 |
| [18] | 张海澜, 王秀明, 张碧星. 井孔的声场和波. 北京: 科学出版社, 2004 . Zhang H L, Wang X M, Zhang B X. Acoustic wavefield and waves in the borehole (in Chinese). Beijing: Science Press, 2004 . |
| [19] | Tang X, Wang T, Patterson D. Multipole acoustic logging-while-drilling.//72nd Annual International Meeting, SEG Expanded Abstracts, 2002, 364-368. http://www.oalib.com/references/18987321 |
| [20] | Press W H, Teukolsky S A, Vetterling W T, et al. Numerical recipes in Fortran 77: The art of scientific computing. Cambridge: Cambridge University Press, 1992 . |
| [21] | 杨文采. 地震波场反演的BG一逆散射方法. 地球物理学报 , 1995, 38(3): 358–366. Yang W C. BG-inverse scattering method for inversion of seismic wavefield. Chinese J. Geophys. (in Chinese) , 1995, 38(3): 358-366. |
 2013, Vol. 56
2013, Vol. 56




