研究证实地球各向异性普遍存在于地下介质中.经过近几十年的发展,传统的各向同性逆时偏移技术不论是在理论上还是在实际生产中都已获得了长足的进步,并逐步趋于成熟[1-5].而各向异性逆时偏移技术的研究仍处于不断的探索和完善过程中[6-9].各向异性因素的考虑对于地震勘探来说至关重要.例如,对于岩下构造或者是盐丘侧翼成像时,未考虑各向异性因素的影响或者是仅仅采用VTI介质假设,会在最终的成像结果中产生走时和振幅的较大误差,使得反射同相轴不连续,能量聚焦较差,从而造成偏移假象.在这种情况下,如果采用具有倾斜对称轴的TTI逆时偏移将会较好地改善成像质量.
各向异性介质逆时偏移研究的理论基础是各向异性全弹性波波动方程,其能更加真实地描述地震波在地球实际介质中的传播.然而,各向异性全弹性波方程逆时偏移计算量较大,并且计算效率低.这对于本身存在对计算机能力要求非常高的逆时偏移算法来讲是非常不可取的.针对于目前仍以纵波勘探为主的现状,仅允许qP波传播的各向异性伪声波方程的研究逐渐成为国内外专家学者研究的热点问题[10-13].Alkhalifah(1998,2000)[14-15]从频散关系出发,提出了著名的声学假设思想,即把沿着对称轴方向的横波速度设为零.并由此推导出VTI介质四阶偏微分伪声波方程.在此基础上,国内外学者对VTI和TTI介质伪声波方程正演模拟以及偏移成像进行了深入研究和探索.吴国忱和梁锴(2005,2007)[16-17]在空间-频率域求解VTI介质伪声波方程.由于四阶偏微分方程求解时较为繁琐,Zhang等(2003)[18]、Zhou等(2006a)[19]、Hestholm(2007)[20]和Du等(2008)[21]推导出VTI介质二阶耦合伪声波方程;Zhou等(2006b)[19]、Zhang和Zhang(2008)[22]、Fletcher等(2008,2009)[23-24]将VTI介质RTM推广到TTI介质中.Duveneck等(2008,2011)[25-26]从胡克定律和质点方程出发,通过修改弹性矩阵中的参数,推导出VTI介质二阶耦合伪声波方程. Duveneck的方法从物理的角度解释了水平应力分量和垂直应力分量的意义.Fowler等(2010)[27]给出了各向异性二阶偏微分伪声波方程的一般形式,并认为它们都是等价的,彼此之间可以相互转化.康玮等(2011)[28]推导出没有声学假设的两个二阶耦合qP和qSV波方程.然而,二阶偏微分伪声波方程进行数值模拟和偏移成像时,在对称轴方向变化梯度较大的区域会出现数值不稳定现象.在声学假设条件下,尽管沿对称轴方向的横波速度设置为零,但是在其他方向上的横波速度仍不为零.从而产生一种低速度、低振幅的qSV波人为干扰.它会严重影响最终的偏移成像效果,所以在逆时偏移成像之前必须进行压制.
针对目前各向异性qP波方程正演和逆时偏移中存在的伪横波噪声问题,基于弱各向异性假设的频散关系,Klie和Toro(2001)[29]在空间-频率域推导出不存在qSV波的适用于任意各向异性强度的VTI介质伪声波方程.Du等(2005)[30]同样在弱各向异性假设条件下,利用泰勒级数展开的方法,推导出TTI介质纯P波方程.然而,研究发现声学假设具有更高的精度.因此,从VTI介质qP-qSV波精确频散关系公式出发,Pestana等(2011)[31-32]利用泰勒近似对频散关系进行了解耦,进而推导出VTI介质纯P波波动方程.同年Zhan等[33]利用旋转波数的概念将其拓展到TTI介质中,给出了相应的二维TTI介质时间-波数域纯P波方程.Chu等(2011)[34]在Liu(2009)[35]给出的解耦的频散关系基础上,采用泰勒近似的方法推导出时间-空间域TTI介质纯P波方程,并对其精度误差进行了分析.此后Zhang等(2009)[36]以及H.Guan等(2011)[37]分别给出一种压制干扰波传播的方法,但是仍有残余伪横波能量存在.黄翼坚和朱光明(2011)[38]通过对精确相速度公式进行多项式近似,推导出近似的VTI介质纯P波方程.然而,该方程需要对系数进行“微调处理”,并且其只有在Thomsen各向异性参数ε和δ相等或相差不大时,才能进行较准确的数值模拟和偏移成像.
本文借助于TTI介质二阶耦合伪声波方程中的辅助波场,给出一种空间域的简单、高效的压制伪横波噪声的方法。模型测试验证了方法的有效性,二维TTI逆掩断层模型实验证实该方法可以进行准确清晰的逆时偏移成像.
2 各向异性介质qP-qSV波波动方程各向异性介质中波的相速度、群速度以及偏振方向准确地描述和刻画了其在传播过程中的特征.将平面谐波解代入到Christoffel方程中就得到了VTI介质qP波、qSV波和SH波的精确相速度公式[39].VTI介质qP-qSV波的精确相速度公式如下所示:
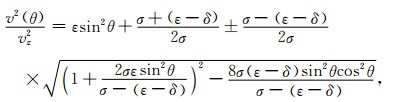
|
(1) |
其中,v(θ)和vz分别是相速度和沿着对称轴方向的速度.θ为关于对称轴的相角.ε和δ是Thomsen各向异性参数.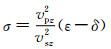
将(1)式变换到频率-波数域,再结合旋转波数可得到精确的二维TTI介质qP-qSV波耦合的频散关系表达式:
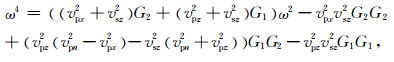
|
(2) |
式中,
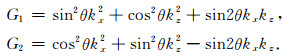
|
(3) |
其中,vpz为垂直于对称平面的qP波速度;vpx=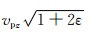
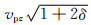
注意到在由方程(1)转换得到方程(2)的过程中,为了求取精确频散关系,在去掉相速度中的根号时,采用等号两边平方的方法,由此产生出除了P波解之外的多余解,这就是qSV波人为干扰产生的根本原因[38].
为了简化计算,需要借助不同的辅助函数将四阶频散关系降为两个二阶的频率-波数域表达式.本文选择不同的辅助函数,进而得到三种具有不同波场快照形式的二阶耦合qP-qSV波波动方程.
(1)选取的辅助函数为

|
(4) |
从而得到如下方程
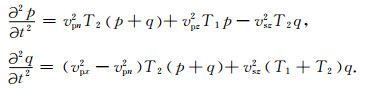
|
(5) |
式中二阶偏导数算子T1和T2分别为
其中p和q分别表示经过降阶处理后得到的二阶耦合qP-qSV波方程中的两个波场值.
(2)选取的辅助函数为
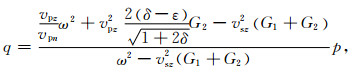
|
(7) |
从而得到如下方程
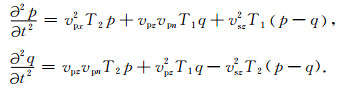
|
(8) |
(3)利用波数旋转将康玮等(2011)[28]在波数域通过投影弹性波方程波场的方法得到的两组新的VTI介质二阶耦合qP波和qSV波方程扩展到TTI介质中,其中qP波方程为
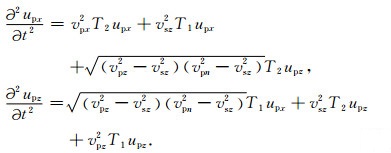
|
(9) |
很显然,对于方程(5)和(7),当采用声学假设vsz=0时,就分别退化为Zhou等(2006b)[19]和Duveneck等(2008)[25]给出的方程形式.
3 完全匹配层吸收边界条件的建立由于研究区域通常是有限的范围,因此正确处理边界附近的反射波问题在数值模拟和偏移过程中显得尤为重要.目前常用的吸收边界条件主要包括三类:第一类是利用一种不同形式的波动方程(如单程波方程)来估计边界处的波场(Clayton和Engquist,1977[40];Reynolds,1978[41];Mur,1981[42];Keys,1985[43]);第二类是由Cerjan等(1985)[44]引入的在边界附近衰减波场(Kosloff,1986[45];Sochacki等,1987[46];Cao和Greenhalgh,1998[47];Sarma等,1998[48];Tian等,2008[49]);第三类就是完全匹配层(PML)吸收边界条件.该边界条件是由Berenger[50]于1994年针对电磁波的传播情况而提出的一种高效的吸收边界.该方法不仅可以完全吸收任意入射角度、任意频率入射的波,而且几乎不产生任何反射.被认为是目前吸收效果最好的边界条件而被广泛应用到多种领域.为了研究qSV波在模型边界附近的吸收衰减情况,本文在各向异性qP-qSV波方程(以方程(5)为例)中引入完全匹配层吸收边界.根据PML的方法原理推导得到方程5相应的时间域完全匹配层控制方程如下(其他类似方程同理可得到):
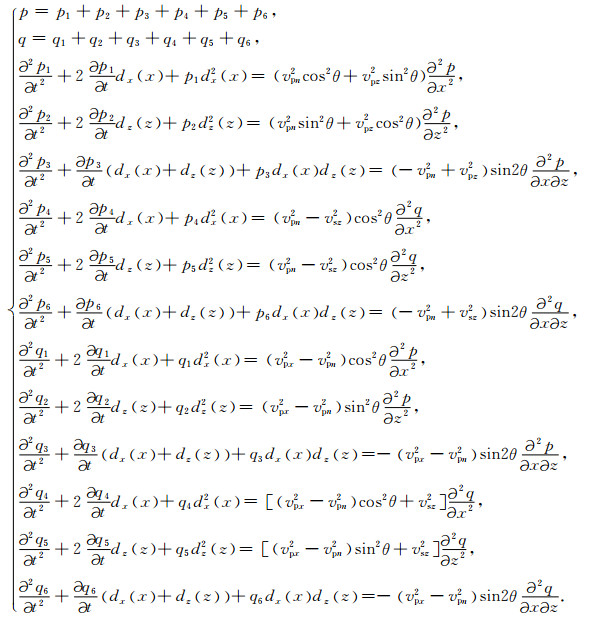
|
(10) |
式中dx(x)和dz(z)分别表示x方向和z方向上的衰减系数.
利用吸收边界(10),模拟了均匀VTI介质中的波场.图 1为VTI中的模拟结果.由图 1可见,完全匹配层吸收条件不仅可以衰减qP波,而且对伪横波噪声在模型边界处也具有较好的吸收效果,并未因为qSV波低振幅、低速度的特征而在边界处引起较大的数值频散.因此,在声学各向异性正演模拟和逆时延拓过程中,选择PML吸收边界条件可以获得理想的效果.还模拟了三种不同波形的TTI介质qP-qSV波方程的波场快照如图 2所示.

|
图 1 p在不同时刻的波场快照(方程(5)) (a)、(b)分别是vs=0m/s时p在t=300ms、t=850ms的波场快照;(c)、(d)分别是vs=1480m/s时p在t=300ms、t=850ms的波场快照.(vpz=3000m/s,ε=0.24,δ=0.05,θ=0). Fig. 1 Wavefield snapshots of p at different time (equation (5)) (a)、(b) show the snapshot of p at t=300ms、t=850ms when vs=0m/s, respectively; (c)、(d) show the snapshot of p att=300ms、t=850ms when vs=1480m/s, respectively.(vpz=3000m/s, ε=0.24, δ=0.05, θ=0). |

|
图 2 不同qP-qSV波波动方程的波场快照 (a)、(b)分别是方程(5)中p和q的波场快照;(c)、(d)分别是方程(8)中p和q的波场快照;(e)、(f)、(g)分别是方程(9)中upx、upz和upx+upz的波场快照. Fig. 2 Wavefield snapshots of different qP-qSV wave equations (a)、(b) show the snapshots of p and q inequation (5), respectively; (c)、(d) show the snapshots of p and q in equation (8), respectively; (e)、(f)、(g) show the snapshots of upx、upz and upx+upzinequation (9), respectively |
从波场快照(图 2)可以看到,在qP波传播的同时在其内部还存在着低振幅、低波速的波型. Grechka(2004)[51]研究发现这是一种qSV波.该干扰波会影响数值模拟的效果和降低逆时偏移成像的品质,即使在vsz=0时仍然不会消失,并且呈现出菱形状(如图 1a所示).此人为干扰产生的根源是在声学假设的情况下,尽管沿对称轴方向的横波速度变成零,但是在其他传播方向上的相速度值并不为零.更重要的是,横波的群速度值也是非零的.它所带来的不仅是噪声干扰问题,由于该横波干扰的波速较小,还会引起较为严重的频散问题,进而影响正演模拟和逆时偏移成像的数值精度.因此,在进行qP波逆时偏移之前必须对此伪横波噪声予以压制或消除.
Tsvankin(2001)[52]研究发现,参数
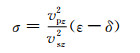
|
(11) |
在很大程度上控制着各向异性介质中qSV波的运动学特征.针对不同情况下的σ,qSV波的波前面表现出不同的形态.当σ的值大约小于0.8时,qSV波的波前三角交叉现象开始消失.Fletcher(2009)[24]认为在上述范围内,选择尽量小的σ,换句话说vsz足够大时就会消除伪横波波前三角,从而可以保障在任意对称轴方向剧烈变化的TTI介质中稳定的波场传播.此外,保证整个研究区域的σ值恒定,可以有效减弱伪横波的各向异性及反射强度.
压制伪横波噪声的一种较为有效的手段是各向异性参数匹配法.在声学假设条件下,通过在研究区域的浅层设置各向同性层或者椭圆各向异性层(Thomsen参数ε等于δ)来消除伪横波噪声的影响.为了进一步降低误差因素的影响,也可以在激发震源的周围设置所谓的震源环.图 3是设置震源环后的波场模拟结果,vsz=0时的波场快照中伪横波噪声得到有效压制,但是在vsz不为零的情况下,qSV波的能量只在一定程度上减弱,残余的能量仍然很强.此类方法改变了介质参数,仅适用于近海勘探环境,对于陆地数据很难得到应用.另外,声学假设得到的qP波方程存在很严重的数值稳定性问题.考虑了vsz不为零的qP-qSV波方程能很好地保证稳定性,但是利用各向异性参数匹配法难以摆脱伪横波噪声的影响(图 3).

|
图 3 波场快照 (a)、(b)、(c)分别是(vsz=0 m/s)方程(5)中p、加各向同性和椭圆各向异性(ε=δ=0.24)震源环的波场快照;(d)、(e)、(f)分别是(vsz=1480m/s)方程(5)中p、加各向同性和椭圆各向异性(ε=δ=0.24)震源环的波场快照(vpz=3000 m/s,ε=0.24,δ=0.05,θ=π/4). Fig. 3 Wavefield snapshots (a)、(b)、(c) show the snapshot of p、the one with isotropic box and elliptical anisotropic box (ε=δ=0.24) in equation (5)(vsz=0 m/s), respectively; (d)、(e)、(f) show the snapshot of p、the one with isotropic box and elliptical anisotropic box (ε=δ=0.24) in equation (5) (vsz=1480 m/s), respectively (vpz=3000 m/s, ε=0.24, δ=0.05, θ=π/4). |
Zhang等(2009)[36]基于特征值分析提出一种波数域的滤波投影方法,取得了较好的压制效果,但是该方法需要对波场进行两次傅里叶变换,极大地增加计算量.对于Zhou等(2006b)[19]给出的二维VTI介质qP波方程(可由方程(5)在θ=0,vs=0时简化得到),其P波的特征波形在波数域表示为

|
(12) |
整理得
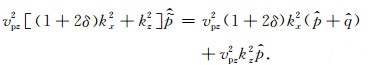
|
(13) |
当|δ|的值较小时,上式简化为
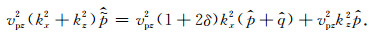
|
(14) |
变换到空间域得
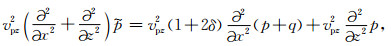
|
(15) |
等式左边相当于对P波的特征波形作用一个线性的拉普拉斯算子,故令
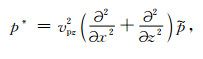
|
(16) |
由于在作用拉普拉斯算子之后,相当于乘上因子-4ω2cos2θ/v2,所以保留等式右端vpz2项,则有
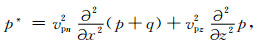
|
(17) |
式中,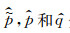
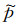
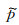
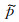
不同学者通过借助辅助函数的方法,对Alkhalifah(2000)[15]推导出的VTI介质四阶qP波方程进行降阶处理,得到了一系列二阶耦合qP波方程.然而,该辅助函数并不具有任何物理含义.Duveneck等(2008,2011)[25-26]从胡克定律和质点运动方程出发,导出了不仅保证正确的P波运动学特征,而且还保持了其物理能量的二阶耦合qP波方程(由方程(7)在vsz=0时退化得到).该方程与各向异性全弹性波波动方程等价.在此方程中两个波场都被赋予了明确的物理含义.康玮等(2011)[28]由各向异性全弹性波波动方程出发推导出一组用正应力表达的二维qP-qSV波方程.将这两个正应力进行线性组合就可得到qP波的波场(如图 2(e,f,g)所示).
鉴于此,本文结合辅助波场给出一种简单、高效的压制伪横波噪声的滤波方法(以方程(5)为例):
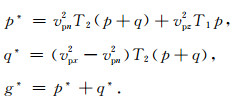
|
(18) |
式中p*和q*分别是滤波后的波场,g*是两个波场的叠加.经过分别滤波然后再叠加处理后,波场快照中的伪横波噪声得到了极大地压制,如图 4所示.研究发现该方法还适用于其他形式的TTI介质二阶耦合qP-qSV波方程,如方程(8)和方程(9).不同的qP-qSV波方程具有与之相对应的压制方程.此外,基于声学假设得到的各向异性二阶耦合qP波方程也获得了很好的压制效果(如图 4所示).

|
图 4
滤波之后的波场快照
(a)、(b)、(c)分别是(vsz=1480 m/s)方程(5)滤波后的p、q和g;(d)、(e)、(f)分别是(vsz=0 m/s) 方程(8)滤波后的p*、q*和g*;(g)、(h)、(i)分别是(vsz=0 m/s)方程(9)滤波后的p*、q*和g*. Fig. 4 Wavefield snapshots after filtered (a)、(b)、(c) show the snapshots of p*、q* and g* after (vsz=1480 m/s) equation (5) filtered, respectively; (d)、(e)、(f) show the snapshots of p*、q* and g* after (vsz=0 m/s) equation (8) filtered, respectively; (g)、(h)、(i) show the snapshots of p*、q* and g* after (vsz=0 m/s) equation (9) filtered, respectively |
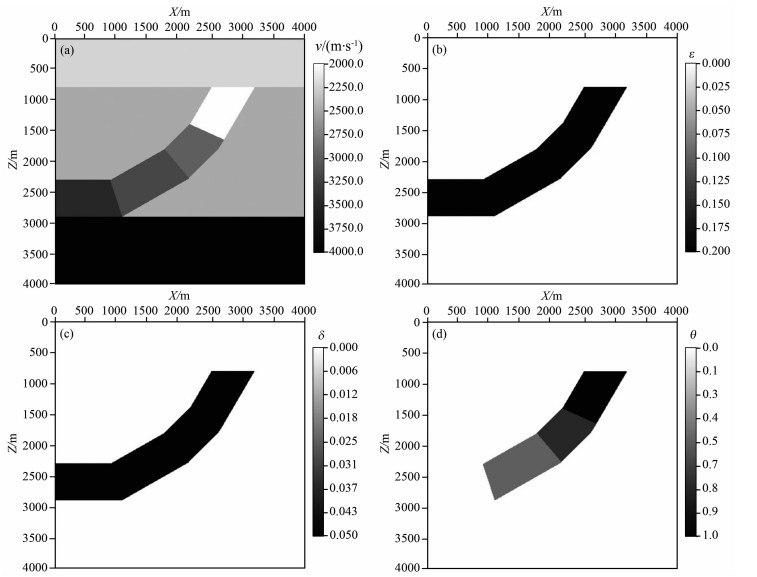
为了检验方法的有效性(以方程(5)为例),本文对一个简单的二维TTI逆掩断层模型进行了测试.该模型空间采样网格为400×400,由镶嵌在各向同性背景上的三段不同倾斜角度的断层所构成,在浅部和底部分别存在一个各向同性层.模型中的参数vpz、ε、δ以及θ值如图 5所示.为了保证正演模拟和逆时偏移过程中的数值稳定性,取σ=0.75.地表激发地面接收,采用25Hz的雷克子波,得到时间长度为2500ms的合成地震记录.逆时延拓差分求解采用时间二阶、空间十阶的规则高阶有限差分方法,差分网格大小10m×10m,完全匹配层吸收边界的厚度L=50.图 6(a,b)分别表示滤波前后的脉冲响应.通过对比显示经过滤波再叠加之后,波场快照中的伪横波噪声得到了极大程度上的消除(黑色方框区域所示).图 6(c,d)显示了二维逆掩断层模型对应于不同偏移算子的成像结果.在各向同性偏移算子得到的图像中,同相轴不连续,反射界面聚焦较差,出现了较为严重的偏移假象,而经过TTI偏移算子逆时延拓成像所获得的结果清晰又准确.
|
图 5 二维TTI逆掩断层模型参数 (a)vpz;(b)ε;(c)δ;(d)θ. Fig. 5 Paramaters of 2D TTI overthrust model (a) The impulse response without filtered; (b) The impulse response after filtered; (c) Isotropic migration result; (d) TTI migration result. |

|
图 6 二维TTI逆掩断层模型测试 (a)滤波前的脉冲响应;(b)滤波后的脉冲响应;(c)各向同性偏移结果;(d)TTI偏移结果. Fig. 6 Test of 2D TTI overthrust model |
TTI介质qP波方程数值模拟和逆时偏移中两大亟需解决的问题是数值稳定性和伪横波噪声的压制.本文主要对后者进行了研究.伪横波的存在所带来的问题不仅仅是噪声干扰,而且还会给方程的数值解法额外地增加一个相应的稳定性条件,并且由于其速度值相对较低会引起较大频散误差,最终严重影响逆时偏移成像的质量和效果.因此,如何高效地压制伪横波噪声和推导稳定的纯p波方程已经成为当前国内外地球物理学者研究的热点问题.本文首先在TTI介质二阶耦合qP波方程中引入PML吸收边界条件,建立了其完全匹配层控制方程.实验证明完全匹配层吸收边界条件不仅能够吸收衰减人工边界附近的qP波,而且对低速度、低振幅的伪横波也有很好的吸收效果.而后结合在各向异性qP波正演模拟和逆时偏移成像过程中经常被忽略的辅助波场信息,在利用成像条件之前,采用一种空间域的简单易行且高效的压制伪横波噪声传播的方法.该方法不仅可以有效压制伪声波各向异性方程中的菱形干扰波,而且还适用于qP-qSV波方程.模型测试显示伪横波噪声得到有效地压制,各向同性偏移算子导致了较为严重的偏移假象,而TTI偏移算子生成了清晰准确的图像.Fletcher(2009)[24]在Vs≠0条件下给出的qP-qSV波方程中σ值的选择较为繁琐,只能在一定程度上保证数值稳定性,并非适用于任意强度的各向异性情况.因此,各向异性纯P波方程的推导以及稳定算法的实现将是下一步研究的重点.
致谢衷心感谢外审专家和编辑部提出的宝贵意见和建议.
| [1] | 丁亮, 刘洋. 逆时偏移成像技术研究进展. 地球物理学进展 , 2011, 26(3): 1085–1100. Ding L, Liu Y. Progress in reverse time migration imaging. Progress in Geophys (in Chinese) , 2011, 26(3): 1085-1100. |
| [2] | 陈可洋. 地震波逆时偏移方法研究综述. 勘探地球物理进展 , 2010, 33(3): 153–159. Chen K Y. Review of seismic reverse time migration methods. Progress in Exploration Geophysics (in Chinese) , 2010, 33(3): 153-159. |
| [3] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Liu B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [4] | 刘红伟, 刘洪, 邹振, 等. 地震叠前逆时偏移中的去噪与存储. 地球物理学报 , 2010, 53(9): 2171–2180. Liu H W, Liu H, Zou Z, et al. The problems of denoise and storage in seismic reverse time migration. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2171-2180. |
| [5] | Yoon K, Marfurt K J, Starr W. Challenges in reverse-time migration: 74th Annual International Meeting, SEG, Expanded Abstracts, MIG 4. 8, 2004. http://www.oalib.com/references/18987292 |
| [6] | 杜启振, 秦童. 横向各向同性介质弹性波多分量叠前逆时偏移. 地球物理学报 , 2009, 52(3): 801–807. Du Q Z, Qin T. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 801-807. |
| [7] | 张美根, 王妙月. 各向异性弹性波有限元叠前逆时偏移. 地球物理学报 , 2001, 44(5): 711–719. Zhang M G, Wang M Y. Prestack finite element reverse-time migration for anisotropic elastic wave. Chinese J. Geophys. (in Chinese) , 2001, 44(5): 711-719. |
| [8] | Dellinger J, Etgen J. Wave-field separation in two-dimensional anisotropic media. Geophysics , 1990, 55(7): 914-919. DOI:10.1190/1.1442906 |
| [9] | Yan J, Sava P. Elastic wavefield separation for VTI media: 78th Annual International Meeting, SEG, Expanded Abstracts, 2008: 2191-2195. http://www.oalib.com/references/18987275 |
| [10] | Yoon K, Sang S, Jean J, et al. Stability and speedup issues in TTI RTM implementation: 80th Annual International Meeting, SEG, Expanded Abstracts, 2010: 3221-3225. http://www.oalib.com/references/18987276 |
| [11] | Ekkehart T. Reverse-time migration in TTI media: 80th Annual International Meeting, SEG, Expanded Abstracts, 2010: 3193-3197. http://www.oalib.com/references/18987277 |
| [12] | Zhang Y, Zhang H Z, Zhang G. A stable TTI reverse time migration and its implementation: 79th Annual International Meeting, SEG, Expanded Abstracts, 2009: 2794-2798. http://www.oalib.com/references/18987278 |
| [13] | Jin S W, Jiang F, Ren Y Q, et al. Comparison of isotropic, VTI and TTI reverse time migration: an experiment on BP anisotropic benchmark dataset: 80th Annual International Meeting, SEG, Expanded Abstracts, 2010: 3198-3203. |
| [14] | Alkhalifah T. Acoustic approximations for processing in transversely isotropic media. Geophysics , 1998, 63(2): 623-631. DOI:10.1190/1.1444361 |
| [15] | Alkhalifah T. An acoustic wave equation for anisotropic media. Geophysics , 2000, 65(4): 1239-1250. DOI:10.1190/1.1444815 |
| [16] | 吴国忱, 梁锴. VTI介质频率-空间域准P波正演模拟. 石油地球物理勘探 , 2005, 40(5): 535–545. Wu G C, Liang K. Quasi P-wave forward modeling in frequency-space domain in VTI media. Oil Geophysical Prospecting (in Chinese) , 2005, 40(5): 535-545. |
| [17] | 吴国忱, 梁锴. VTI介质qP波方程高精度有限差分算子. 地球物理学进展 , 2007, 22(3): 896–904. Wu G C, Liang K. High precision finite difference operators for qP wave equation in VTI media. Progress in Geophysics (in Chinese) , 2007, 22(3): 896-904. |
| [18] | Zhang L B, Rector J W III, Hoversten G M. An acoustic wave equation for modeling in tilted Ti media: 73rd Annual International Meeting, SEG, Expanded Abstracts, 2003: 153-156. |
| [19] | Zhou H B, Zhang G Q, Bloor R. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media: 76th Annual International Meeting, SEG, Expanded Abstracts, 2006: 194-198. http://www.oalib.com/references/18987281 |
| [20] | Hestholm S. Acoustic VTI modeling using high-order finite-differences: 77th Annual International Meeting, SEG, Expanded Abstracts, 2007, 26(1): 139-143. http://www.oalib.com/references/18987282 |
| [21] | Du X, Fletcher R, Fowler P J. A new pseudo-acoustic wave equation for TI media: Presented at the 70th Annual International Conference and Exhibition, EAGE, 2008. http://www.oalib.com/references/18987283 |
| [22] | Zhang Z H, Zhang Y. Reverse time migration in 3D heterogeneous TTI media: 78th Annual International Meeting, SEG, Expanded Abstracts, 2008: 2196-2200. http://www.oalib.com/references/18988265 |
| [23] | Fletcher R, Du X, Fowler P J. A new pseudo-acoustic wave equation for TI media: 78th Annual International Meeting, SEG, Expanded Abstracts, 2008: 2082-2086. http://www.oalib.com/references/18987285 |
| [24] | Fletcher R P, Du X, Fowler P J. Reverse time migration in tilted transversely isotropic (TTI) media. Geophysics , 2009, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902 |
| [25] | Duveneck E, Milik P, Bakker P M. Acoustic VTI wave equations and their application for anisotropic reverse-time migration: 78th Annual International Meeting, SEG, Expanded Abstracts, 2008: 2186-2190. http://www.oalib.com/references/18987300 |
| [26] | Duveneck E, Bakker P M. Stable P-wave modeling for reverse-time migration in tilted TI media. Geophysics , 2011, 76(2): S65-S75. DOI:10.1190/1.3533964 |
| [27] | Fowler P J, Du X, Fletcher R P. Coupled equations for reverse time migration in transversely isotropic media. Geophysics , 2010, 75(1): S11-S22. DOI:10.1190/1.3294572 |
| [28] | Kang W, Cheng J B. Prestack scalar reverse time migration of elastic seismic data in TI media: 81st Annual International Meeting, SEG, Expanded Abstracts, 2011: 3367-3371. |
| [29] | Kie H, Toro W. A new acoustic wave equation for modeling in anisotropic media. SEG Expanded Abstracts , 2001: 1171-1174. |
| [30] | Du X, Bancroft J C, Lines L R. Reverse-time migration for tilted TI media. SEG Expanded Abstracts , 2005: 1930-1933. |
| [31] | Pestana R C, Stoffa P L. Time evolution of the wave equation using rapid expansion method. Geophysics , 2010, 75(4): T121-T131. DOI:10.1190/1.3449091 |
| [32] | Pestana R C, Ursin B, Stoffa P L. Separate P-and SV-wave equations for VTI media. 2011 SEG Annual Meeting, Society of Exploration Geophysicists, 2011: 163-167. http://www.oalib.com/references/18987265 |
| [33] | Ge Zhan, Pestana R C, Stoffa P L. An acoustic wave equation for pure P wave in 2D TTI media: 81st Annual International Meeting, SEG, Expanded Abstracts, 2011: S168-S173. http://www.oalib.com/references/18987301 |
| [34] | Chu C L, Macy B K. An accurate and stable wave equation for pure acoustic TTI modeling: 81st Annual International Meeting, SEG, Expanded Abstracts, 2011: 179-184. http://www.oalib.com/references/18987266 |
| [35] | Liu F Q, Morton S A, Jiang S S, et al. Decoupled wave equations for P-and SV-waves in an acoustic VTI media: 79th Annual International Meeting, SEG, Expanded Abstracts, 2009, 28:2844-2848. http://www.oalib.com/references/18987267 |
| [36] | Zhou H Z, Zhang G Q. Removing S-wave noise in TTI reverse time migration: 79th Annual International Meeting, SEG, Expanded Abstracts, 2009: 2849-2853. http://www.oalib.com/references/18987268 |
| [37] | Guan H, Dussaud E. Techniques for an efficient implementation of RTM in TTI media: 81st Annual International Meeting, SEG, Expanded Abstracts, 2011: 3393-3397. http://www.oalib.com/references/18987269 |
| [38] | 黄翼坚, 朱光明, 刘池洋. 一个近似的VTI介质声波方程. 地球物理学报 , 2011, 54(8): 2117–2123. Huang Y J, Zhu G M, Liu C Y. An approximate acoustic wave equation for VTI media. Chinese J. Geophys. (in Chinese) , 2011, 54(8): 2117-2123. |
| [39] | Tsvankin I. P-wave signatures and notation for transversely isotropic media: An overview. Geophysics , 1996, 61(2): 467-483. DOI:10.1190/1.1443974 |
| [40] | Clayton R W, Engquist B. Absorbing boundary conditions for acoustic and elastic wave equations. Bulletin of the Seismological Society of America , 1977, 67(6): 1529-1540. |
| [41] | Reynolds A C. Boundary conditions for the numerical solution of wave propagation problems. Geophysics , 1978, 43(6): 1099-1110. DOI:10.1190/1.1440881 |
| [42] | Mur G. Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations. IEEE Transactions on Electromagnetic Compatibility , 1981, EMC-23(4): 377-382. DOI:10.1109/TEMC.1981.303970 |
| [43] | Keys R G. Absorbing boundary conditions for acoustic media. Geophysics , 1985, 50(6): 892-902. DOI:10.1190/1.1441969 |
| [44] | Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equation. Geophysics , 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |
| [45] | Kosloff R, Kosloff D. Absorbing boundaries for wave propagation problems. Journal of Computational Physics , 1986, 63(2): 363-376. DOI:10.1016/0021-9991(86)90199-3 |
| [46] | Sochacki J, Kubichek R, George J, et al. Absorbing boundary conditions and surface waves. Geophysics , 1987, 52(1): 60-71. DOI:10.1190/1.1442241 |
| [47] | Cao S, Greenhalgh S. Attenuating boundary conditions for numerical modeling of acoustic wave propagation. Geophysics , 1998, 63(1): 231-243. DOI:10.1190/1.1444317 |
| [48] | Sarma G S, Mallick K, Gadhinglajkar V R. Nonreflecting boundary condition in finite-element formulation for an elastic wave equation. Geophysics, , 1998, 63(3): 1006-1016. DOI:10.1190/1.1444378 |
| [49] | Tian X B, Kang I B, Kim G Y, et al. An improvement in the absorbing boundary technique for numerical simulation of elastic wave propagation. Journal of Geophysics and Engineering , 2008, 5(2): 203-209. DOI:10.1088/1742-2132/5/2/007 |
| [50] | Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics , 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [51] | Grechka V, Zhang L B, Rector J W. Shear waves in acoustic anisotropic media. Geophysics , 2004, 69(2): 576-582. DOI:10.1190/1.1707077 |
| [52] | Tsvankin I. Seismic signatures and analysis of reflection data in anisotropic media. New York: Elsevier, 2001 . |
 2013, Vol. 56
2013, Vol. 56

