2. 西部灾害与环境力学教育部重点实验室兰州大学, 兰州 730000;
3. 广西隐伏金属矿产勘查重点实验室桂林理工大学地球科学学院, 桂林 541004;
4. 中国石化集团国际石油勘探开发有限公司, 北京 100083;
5. 东方地球物理公司国际勘探事业部, 河北 涿州 072751;
6. 中国地震局兰州地震研究所, 兰州 730000;
7. 地质科学与矿产资源学院兰州大学, 兰州 730000
2. The Key Laboratory of Mechanics on Disaster and Environment in Western China & Lanzhou University, Lanzhou 730000, China;
3. Guangxi Key Laboratory of Hidden Metallic Ore Deposits Exploration, College of Earth Sciences & Guilin University of Technology, Guilin, 541004, China;
4. Sinopec International Petroleum Exploration and Production Corporation, Beijing 100083, China;
5. BGP International, CNPC, Zhuozhou Hebei 072751, China;
6. Lanzhou Institute of Seismology, China Earthquake Administration, Lanzhou 730000, China;
7. School of Earth Sciences & Lanzhou University, Lanzhou 730000, China
地球内部流体的存在和岩石各向异性是地下介质的两大表征.同时考虑地下流体和各向异性问题,是当今地震学和地球物理学理论与应用研究的前沿和难题之一.在地壳中引起地震各向异性的主要因素,是地壳中存在充满液体的定向排列的裂隙[1].不同的地质事件对应的应力和应变条件不同,自然断裂系统中不同尺度的裂隙呈现出混合交织的复杂图案.地下介质中受多期构造运动的作用,常常发育多组定向排列的断裂,并且断裂尺度从毫米级至米级均有分布,不同尺度的裂隙对地震各向异性影响不同,从而造成了地震各向异性对于频率的依赖性.介质同时存在着微小孔隙并可能充填各种流体.地震波通过时会导致流体在断裂及与断裂相通的孔隙中流动,从而导致波的频散和衰减.因此通过分析地震波穿过充填流体多尺度断裂介质的地震波响应对研究地壳各向异性和多相介质及断裂型油气藏有着非常重要的意义.
在长波长范畴内,破裂岩石弹性响应用等效介质理论描述,已存在多种理论.如Schoenberg [2-3]的线性滑动模型、Hudson[4-5]的不连通的硬币形包裹体模型、Nishizawa[6]定向排列裂隙模型、Thomsen理论[7-8]假设只适合于低频范围的等径孔隙理论等.但是这些各向异性模型假设与频率无关,因此不能区分微裂隙和宏观裂缝.Thomsen(1995)证明了地震波通过时断裂和等径孔隙之间流体交换对计算各向异性弹性性质有显著影响.Hudson等和Tod[9]推广Thomsen的思想到整个频率范围,他们考虑了各种流动机制,包含波长尺度的流动,以及不同取向断裂之间以及断裂和岩石骨架之间的流动.Van der Kolk等[10]考虑了近排齐裂隙情况下Hudson模型,并考虑裂隙的内部联通.Chapman[11]着眼于颗粒、断裂两种尺度提出了等效介质模型,该模型既基于破裂多孔岩石中的喷流机制,它考虑了球形孔隙和椭圆形微裂隙,其大小等于颗粒尺度,又基于排齐的断裂,其大于颗粒尺度.因此,该理论考虑了两个不同的长度尺度,最终介质是横向各向同性.该模型分别与Brown和Korringa[12]的低频范围及Hudson的高频范围的结果一致.在没有断裂时,它退化为早期的Chapman,Zatsepin和Crampin[13]的颗粒尺度喷流模型[13].这个模型对实验室测量的检验已由Chapman[13-14]讨论了.国内外,多位学者对各向异性介质中地震波速和衰减各向异性进行了理论和应用方面较为深入的研究[15-31],指出了S波分裂现象的存在,充填流体时的响应特征,得到地震各向异性随横波频率的变化.在含流体多组分孔隙各向异性介质中,也存在地震各向异性随频率的变化[32-33].
理论上,波速、衰减因子及其在空间和时间上的变化可以由裂隙密度、微裂隙的排列方向和断裂中填充物的性质决定,因此可以用来认识断裂的分布状况.本文基于等效介质理论[11],用波速、衰减、横波分裂等参数研究HTI介质中厘米至米级的断裂大小、各向异性及频率之间的关系.研究多尺度断裂与流体对各向异性的影响.
2 等效介质中的弹性参数本文的模型基于微结构孔隙弹性理论的HTI介质,即含垂向分布的断裂.文中,“断裂(fracture)”指中等尺度(或地层尺度)的流体单元,其量级为厘米至米级,远小于地震波波长;具有微小尺寸颗粒的微裂缝称为“裂隙(crack)”,其尺寸小于“断裂(fracture)”;球形孔隙(pore)其大小与颗粒和“裂隙”尺寸相当.
我们采用Chapman提出的等效介质模型来描述裂隙和断裂诱导的各向异性.该模型基于破裂多孔岩石中的喷流机制,它同时考虑了Biot的孔隙流体总体流动与裂隙断裂中的流体喷流,但又与BISQ模型不同[34].它的弹性(刚度)张量为复数形式,包含有衰减因子.
模型的弹性(刚度)张量中加入与频率有关受断裂影响的项:
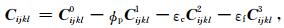
|
(1) |
其中,C ijkl0是具有拉梅参数λ和μ的岩石骨架的各向同性弹性张量,C ijkl1、C ijkl2和C ijkl3分别是孔隙、裂隙和断裂的附加弹性张量,Φp为孔隙度、εc为裂隙密度,εf为断裂密度.这些校正项是拉梅参数、流体性质、断裂性质、频率及时间尺度参数τ(与喷流有关)的函数.C ijkl1、C ijkl2和C ijkl3的计算见附录A.计算出VTI介质的弹性参数后,对VTI介质进行90°的旋转,其对称轴为水平方向,即HTI介质.
为了使Chapman(2003)模型更好地应用于流体充填,Chapman等(2003)采用某一频率(f0)测定岩石速度V p0和V s0以及密度ρ计算Lame参数λ0和μ 0.用C0(Λ,Μ)定义某一频率测定的速度的弹性参数,这样用实验中测定得到Lame参数来直接标定Chapman模型.即
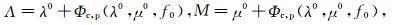
|
(2) |
这里Φc,p指的是与εc和Φp成正比的由裂隙和孔隙引起的弹性参数校正,具体计算参见附录中不包括断裂校正的部分.
并有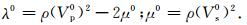
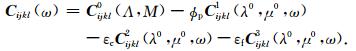
|
(3) |
忽略外力作用时各向异性介质中的波动方程为:
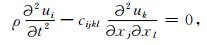
|
(4) |
假定HTI介质中波满足波动方程的平面波位移函数解为:
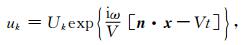
|
(5) |
其中,Uk是位移振幅,x=(x,y,z)T为位置矢量;n=(sinθcosφ,sinθsinφ,cosθ)T为平面波的传播方向,θ为平面波传播的极化角,φ是平面波传播的方位角,ω为圆频率,V为复速度.
把(5)式带入波动方程(4),当极化角θ=π/2时,经过推导与整理可得等效HTI介质中随方位变化的平面波复速度V、逆品质因子1/Q表示的衰减分别为:
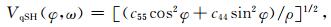
|
(6) |
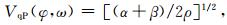
|
(7) |

|
(8) |
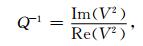
|
(9) |
其中

|
(10) |

|
(11) |
上述方程中所用的弹性参数是等效介质模型中所得出的HTI介质中的弹性参数,与普通的弹性参数不同,它们与频率、断裂尺度、流体因子等有关,为复数形式.由此可见,等效HTI介质中地震波速度、逆品质因子不仅存在方位各向异性,而且还是频率的函数,也与裂隙和断裂中流体性质有关.以上结果不仅考虑了裂隙-断裂诱导的各向异性,而且也考虑了裂隙和断裂内流体性质的影响.
4 HTI介质中频率依赖的各向异性与多尺度断裂的关系 4.1 HTI介质中的Thomsen参数与多尺度断裂的关系Thomsen参数是常见的弱各向异性介质特征参数.假定地震波在(x,y)平面内传播时,则HTI介质中的Thomsen参数为[35]

|
(12) |
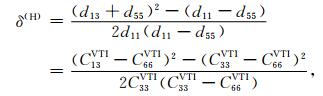
|
(13) |
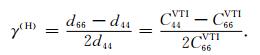
|
(14) |
为了区别于VTI介质的Thomsen参数,HTI介质中将其中的参数加“H”,三个各向异性参数与VTI介质中的意义基本相同,只是γ (H)表示快、慢横波速度的差异程度,在弱各向异性的假设下,γ (H)近似等于断裂密度.通过Thomsen参数可以直观地了解各向异性的物理意义,也为利用地震属性来反演各向异性介质参数架起一座桥梁.
4.2 HTI介质中横波分裂与多尺度断裂的关系根据横波分裂理论,横波通过各向异性介质时要分裂成两种波,一种是偏振方向与断裂走向平行,速度较快的纯剪切波(VSH),另一种是偏振方向垂直于断裂走向,速度较慢的拟剪切波(VSV),在这种情况下,定义横波分裂因子为:
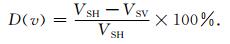
|
(15) |
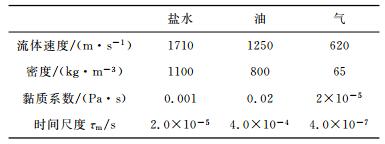
我们分别对饱含流体的裂隙介质中地震波速度、各向异性因子以及逆品质因子(1/Q)值进行数值计算.模型参数的选择为:背景介质是在100Hz不含断裂饱和盐水时测定的,纵波速度为4000m/s,横波速度为2500m/s,密度为2600kg/m3,颗粒尺度为200μm,裂隙半径200μm,纵横比为0.0001.流体参数如表 1所示,断裂尺度分别为0.0002m、0.01m、0.1m、1m及10m,波在xoy平面中传播,极化角为90°,研究波的方位各向异性特征.
|
|
表 1 计算中使用的流体参数 Table 1 The fluid properties used in the calculations |
在等效介质模型中,裂隙密度对波速有重要影响.裂隙密度分别取0.02、0.04、0.06和0.08,引入铅垂分布的断裂,断裂密度为0.05,半径为1m,波的传播方向φ为70°,研究等效介质的横波分裂和方位各向异性.
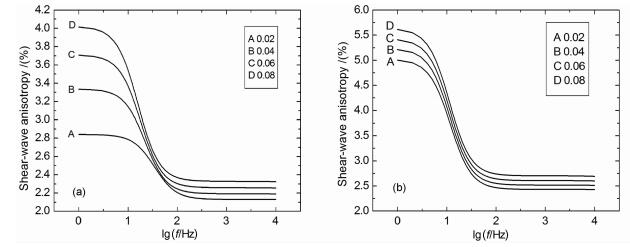
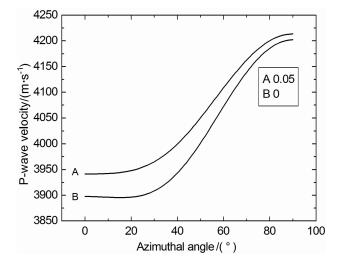
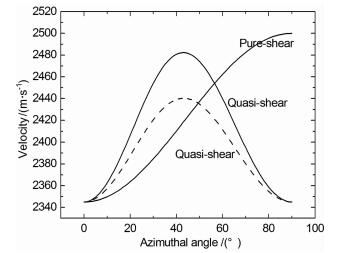
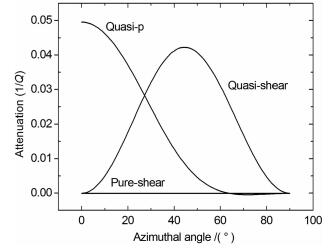
图 1表明在孔隙度为0时,横波分裂因子随裂隙密度的增加而增加,随着频率增加而减小,当频率超过100Hz以后,横波各向异性随频率增大而不变.当孔隙度增加为0.1时,各向异性的变化与前述相似,随断裂密度增加各向异性增加幅度变小.图 2表明不同的断裂尺度P波速度随方位的变化规律:断裂半径在0.01m和0.1m时随方位角增大P波速度增大,在90°达到最大,而半径在1m和10m时在45°达到最小.图 3表明P波速度在断裂半径为0.1m时随裂隙密度的变化,随裂隙密度增大P波速度变小,在方位角比较小时,不考虑裂隙密度速度,误差会比较大,随方位角增大误差则减小.图 4为横波速度方位各向异性的变化,纯横波随方位角增加速度变大,拟横波在42°方位附近时达到最大,随裂隙密度增加横波速度变小.图 5为衰减系数随方位的变化,拟P波随方位增加而减小,拟横波随方位在45°时达到最大,纯横波不随方位变化.可能是由于当孔隙度较大时,流体可以从断裂进入背景介质岩石中,而在0孔隙度时,由于被挤压的流体被迫进入微裂隙中,这样导致各向异性更多依赖于裂隙密度εc参数.
|
图 1 不同裂隙密度横波分裂 (a)Φp=0;(b)Φp=0.1. Fig. 1 Shear-wave anisotropy of different crack density |

|
图 2 不同断裂尺度时qP速度随方位角的变化 Fig. 2 qP velocity as a function of azimuthal angle for different facture radius |
|
图 3 不同裂隙密度时qP速度随方位角变化(断裂半径0.1m, 频率40Hz) Fig. 3 qP velocity as a function of azimuthal angle for different crack density and frequency 40 Hz, fracture radius is 0.1 m 10% porosity |
|
图 4 不同裂隙密度剪切波速度随方位角变化(点划线代表εc=0.05, 实线代表εc=0, 断裂尺寸10cm) Fig. 4 Shear velocity as a function of angle for 10% porosity and frequency 40 Hz, The dashed lines assume εc=0.05, the solid lines εc=0.0, a fracture size of 10 cm |
|
图 5 三种波的逆品质因子1/Q随方位角变化(频率为40Hz, 断裂尺寸10cm) Fig. 5 Angular variation of attenuation for qP-, qS-and S-wave for a frequency of 40 Hz and a fracture size of 10cm |
考虑不同流体充填物对各向异性的影响.研究三种流体:盐水、油和气,它们的属性如表 1所示.断裂孔隙里面充填不同流体时,需要考虑三方面的影响,首先是密度的影响,其次是流体体积模量的影响,还有黏滞系数的影响.由于时间尺度因子τm与流体黏滞系数成比例,因此流体的黏滞系数的影响可以归为τm的影响.考查不同频率下流体对各向异性的影响:断裂为垂向方向,密度为0.05,半径为1m,裂隙密度εc=0,孔隙度为10%.
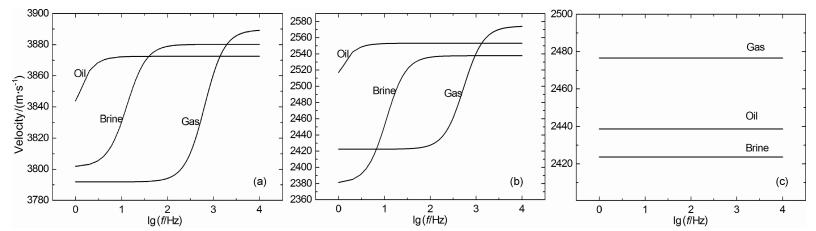
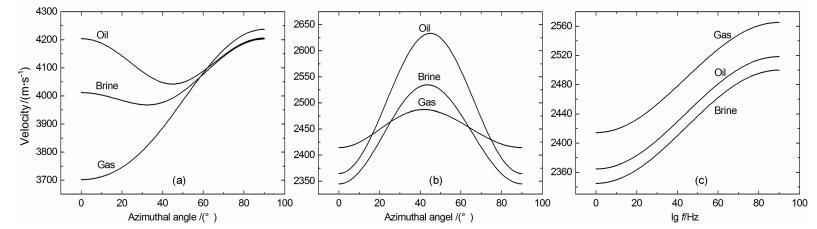
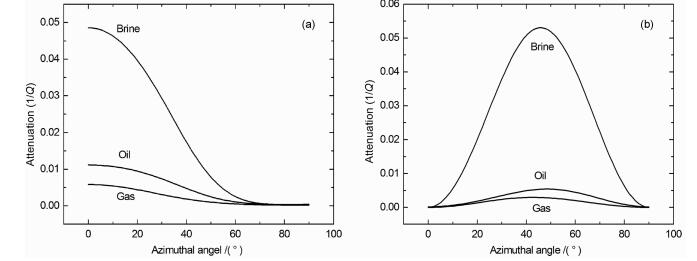
图 6是充填物为油、气、盐水,方位角为45°时qP、qSV和SH波速度随频率变化,对P波在低频时充填物为油时速度最大,为气时最小,在高频时含盐水时速度最大,含气时速度随频率增加而增大,含油时频率增加到90Hz左右,速度随频率增加而不变.拟横波速度随频率变化,在低频时三者速度相差比较大,高频时三者速度趋于一致.纯横波(SH波)速度随频率的变化是,三者速度随频率增加速度不变,含气时速度最大,含盐水时速度最小.图 7是qP、qSV和SH波速度随方位变化特征,含盐水和油时在方位45°附近变成最小,含气时速度随方位角增大单调增加.拟横波速度随方位变化在三种填充物时变化特征相近,但变化幅度不同,纯横波(SH波)速度随方位变化特征是:随方位角增加含三种填充物时速度都是增加.图 8是含三种充填物时qP和qSV波衰减随方位的变化特征,随方位角增大三者衰减变小,含油和气时衰减更接近.拟S波衰减随方位的变化特征,在45°时衰减达到最大.可见存在不同充填物时,其密度和黏滞系数不同,其速度随频率的变化也不同,具有频率依赖性.随方位变化,速度和衰减系数也发生变化,有方位各向异性,填充物为盐水时衰减随方位变化更显著,为油时次之,而填充物为气时衰减随方位变化最小.速度随方位的变化:同一方位时P波和qSV波均是含油时速度最大,含水时次之,含气时速度最小;不同方位时,速度随方位变化趋势是相似的,但幅值不同.
|
图 6 含油、气、盐水P (a)、qSV (b)和SH (c)波速度随频率变化(断裂尺度1m, 方位角45°) Fig. 6 qP (a)、Quasi-shear (b) and Pure-shear (c) velocity for propagation at 45° to the fracture normal as a function of frequency for three different saturations.Fracture size is 1 m |
|
图 7 含油、气和盐水时P (a)、qSV (b)和SH (c)波速度随方位角变化(频率10Hz, 断裂尺度1m) Fig. 7 qP (a)、Quasi-shear (b) and Pure-shear (c) velocity as a function of azimuthal angle for three different saturations.The frequency is 10 Hz.Fracture size is 1 m |
|
图 8 含油气水qP (a)和qSV (b)波的1/犙随方位角变化(频率10Hz, 断裂1m) Fig. 8 Angular variation of attenuation for of three saturations.The frequency is 10 and fracture size is 1 m |
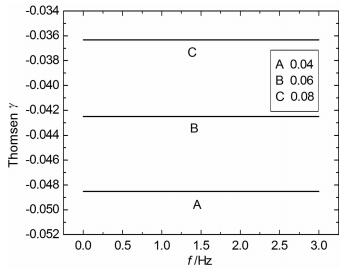
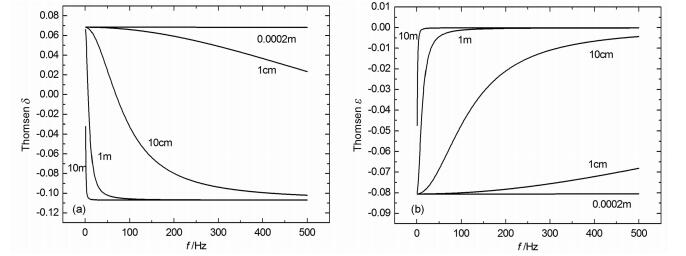
图 9为不同断裂半径时剪切波各向异性随频率的变化,对于微裂隙,随着频率增加,剪切波各向异性不变,而对于大于微裂隙的断裂尺度,均是随频率增加各向异性减小.随裂隙密度增大、孔隙度增大,不同断裂半径的剪切波各向异性随频率的变化趋势相似,但幅值增大,对于断裂尺度为10m,频率较大时各向异性不变.图 10表明,Thomsen参数γ随频率变化而不发生变化,只与裂隙密度有关,可见γ参数没有频率依赖性.图 11为不同断裂半径时Thomsen参数δ和ε随频率变化特征,在低频时其对断裂尺度参数更敏感.随着断裂的增大,Thomsen参数对频率的敏感度增大;不同裂隙尺度范围内的Thomsen参数变化趋势和幅度不同,尺度越大,Thomsen参数随频率的变化速率越快.微裂隙随频率的增加,Thomsen参数不变,裂隙尺度在1~10cm范围内,断裂随频率的增加,Thomsen参数变化比较缓慢,而在地震频带内1~10m范围内的断裂随频率增加迅速的变化.总体上Thomsen参数ε与频率成正比关系,而Thomsen参数δ与频率成反比关系.在地震频带1~10m范围内的中尺度范围的断裂可以用Thomsen参数区分,因此可以在低频时使用Thomsen参数来指示中等尺度的断裂大小.

|
图 9 剪切波各向异性随频率和断裂尺度的变化(方位角70°, 裂隙密度0.02) (a)Φp=0;(b)Φp=0.1. Fig. 9 Shear-wave anisotropy as a function of frequency and various fracture scales, with different porosity and a crack density of 0.02.Propagation is at 70° to the fracture normal |
|
图 10 Thomsenγ随裂隙密度和频率的变化 Fig. 10 Thomsen γ as a function of crack density and frequency |
|
图 11 Thomsen δ(a)和ε(b)随断裂尺度和频率变化(方位角70°, 孔隙度为0.1, 裂隙密度0.02) Fig. 11 Thomsen δ(a) and ε(b) as a function of frequency for various fracture scale with 10% porosity and a crack density of 0.02.Propagation is at 70° to the fracture normal |
根据Chapman提出的等效介质模型,运用数值分析方法通过速度和品质因子(1/Q)研究多尺度断裂和流体对介质各向异性的影响.结果表明当断裂定向分布时,参数结果显示为各向异性,不同断裂尺度具有不同的波速频散和衰减特性,微裂隙密度对各向异性有重要的影响,同时孔隙度对各向异性的程度也有影响.当充填油、气和盐水时,三种充填物的流体性质对各向异性和衰减有重要的作用.在较低频率时Thomsen参数在不同断裂尺度时,随频率依赖性更加敏感,因此可以使用Thomsen参数预测断裂尺度.在低频段,大尺度断裂横波分裂程度更明显,而在高频段,横波各向异性对裂隙敏感度较高,据此可以用来判别微裂隙的方位.根据快慢横波分裂来判定中等尺度断裂的方位及各向异性程度,使得横波分裂判别断裂大小变为可能,这些性质将对断裂的时空探测及介质所充填流体的识别提供理论依据.
附录简单的给出频率依靠横向各向同性的弹性参数由Chapman(2003)[15]给出.孔隙空间由三部分组成,球形空间的孔隙度Φp、裂隙密度εc和断裂密度εf,裂隙的半径af,断裂的密度遵循Hudson(1981)[4]定义的Na3/V,N是体积为V的断裂的数目,a是断裂的半径,微裂隙和孔隙具有相同的颗粒尺寸ζ.
从分析中有两种尺度的常数τm和τf,第一个常数τm微结构喷流频率,它由Chapman(2003)[15]给出:
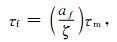
|
(1) |
Chapman(2003)[15]进一步定义:
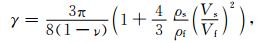
|
(2) |
这里Vs代表剪切波速度,Vf是流体的纵波速度,ρf和ρs是流体密度和饱和岩石密度.υ是泊松比,kf是流体体积模量,定义
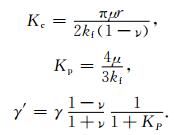
|
(3) |
如果假定裂隙纵横比足够小使KC < < 1,则模型能用只依赖于裂隙密度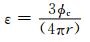
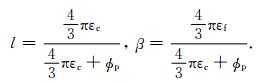
|
(4) |
引入ω作为角频率,用频率表达下面函数:
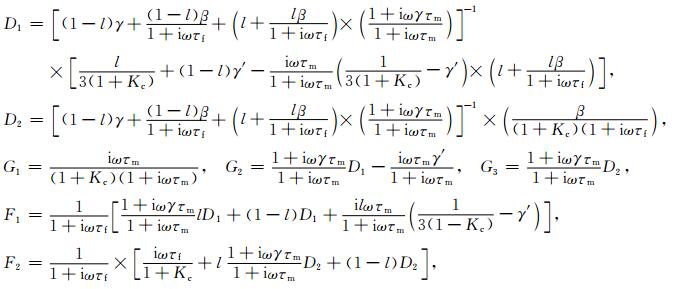
|
(5) |
λ和μ是弹性模量,k是体积模量,
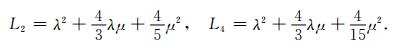
|
(6) |
给出取决于频率的弹性参数,X3代表对称轴的方向(断裂法线方向),5个独立的弹性参数是:
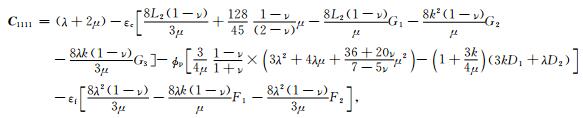
|
(7) |

|
(8) |
本文工作得到中国科学院地质与地球物理研究所张忠杰研究员的热心帮助和建议,在此表示衷心感谢.
| [1] | Crampin S, Booth D C. Shear-wave polarizations near the North Anatolian Fault-II, Interpretation in terms of crack-induced anisotropy. Geophys. J. R Astron. Soc. , 1985, 83(1): 75-92. DOI:10.1111/j.1365-246X.1985.tb05157.x |
| [2] | Schoenberg M. Elastic wave behavior across linear slip interfaces. Journal of the Acoustical Society of America , 1980, 68(5): 1516-1521. DOI:10.1121/1.385077 |
| [3] | Schoenberg M, Douma J. Elastic wave propagation in media with parallel fractures and aligned cracks. Geophys. Prospect. , 1988, 36(6): 571-590. DOI:10.1111/gpr.1988.36.issue-6 |
| [4] | Hudson J A. Wave speeds and attenuation of elastic waves in material containing cracks. Geophys. J. Int. , 1981, 64(1): 133-150. DOI:10.1111/j.1365-246X.1981.tb02662.x |
| [5] | Hudson J A, Liu E, Crampin S. The mechanical properties of materials with interconnected cracks and pores. Geophys. J. Int. , 1996, 124(1): 105-112. DOI:10.1111/gji.1996.124.issue-1 |
| [6] | Nishizawa O. Seismic velocity anisotropy in a medium containing oriented cracks-transversely isotropic case. Journal of Physics of the Earth , 1982, 30(4): 331-347. DOI:10.4294/jpe1952.30.331 |
| [7] | Thomsen L. Weak elastic anisotropy. Geophysics , 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [8] | Thomsen L. Elastic anisotropy due to aligned cracks in porous rock. Geophys. Prospect. , 1995, 43(6): 805-829. DOI:10.1111/gpr.1995.43.issue-6 |
| [9] | Tod S R. The effects on seismic waves of interconnected nearly aligned cracks. Geophysical Journal International , 2001, 146(1): 249-263. DOI:10.1046/j.1365-246X.2001.00451.x |
| [10] | Van der Kolk C M, Guest W S, Potters J H H M. The 3D shear experiment over the Natih field in Oman: the effect of fracture-filling fluids on shear propagation. Geophys. Prospect. , 2001, 49(2): 179-197. DOI:10.1046/j.1365-2478.2001.00250.x |
| [11] | Chapman M. Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity. Geophys. Prospect. , 2003, 51(5): 369-379. DOI:10.1046/j.1365-2478.2003.00384.x |
| [12] | Brown R J S, Korringa J. On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid. Geophysics , 1975, 40(4): 608-616. DOI:10.1190/1.1440551 |
| [13] | Chapman M, Zatsepin S V, Crampin S. Derivation of a microstructural poroelastic model. Geophys. J. Int. , 2002, 151(2): 427-451. DOI:10.1046/j.1365-246X.2002.01769.x |
| [14] | Chapman M H. Modelling the wide-band laboratory response of rock samples to fluid and pressure changes[Ph.D.thesis]. Edinburgh: University of Edinburgh, 2001. http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.642749 |
| [15] | Chapman M, Maultzsch S, Liu E R, et al. The effect of fluid saturation in an anisotropic multi-scale equant porosity model. J. Appl. Geophys. , 2003, 54(3-4): 191-202. DOI:10.1016/j.jappgeo.2003.01.003 |
| [16] | Chapman M, Liu E R, Li X Y. The influence of fluid sensitive dispersion and attenuation on AVO analysis. Geophysical Journal International , 2006, 167(1): 89-105. DOI:10.1111/gji.2006.167.issue-1 |
| [17] | Champan M. Modeling the effect of multiple sets of mesoscale fractures in porous rock on frequency-dependent anisotropy. Geophysics , 2009, 74(6): D97-D103. DOI:10.1190/1.3204779 |
| [18] | 张中杰, 滕吉文, 贺振华. EDA介质中地震波速度、衰减与品质因子方位异性研究. 中国科学(E辑) , 2009, 29(6): 569–574. Zhang Z J, Teng J W, He Z H. The detection attenuation research on seismic wave velocity 'Attenuation' quality factor of EDA medium. Science in China (Ser. E) (in Chinese) , 2009, 29(6): 569-574. |
| [19] | 张忠杰. 多分量地震资料的各向异性处理与解释方法. 哈尔滨: 黑龙江教育出版社, 2002 . Zhang Z J. Multi-component Seismic Data Anisotropic Processing and Interpretation Methods (in Chinese). Harbin: Heilongjiang Education Press, 2002 . |
| [20] | 何樵登, 张中杰. 横向各向同性介质中地震波及其数值模拟. 长春: 吉林大学出版社, 1996 . He Q D, Zhang Z J. Wave in Transversely Isotropic Medium and Numerical Modelling (in Chinese). Changchun: Jilin University Press, 1996 . |
| [21] | Zhang Z J, Teng J, Badal J, et al. Construction of regional and local seismic anisotropic structures from wide-angle seismic data: crustal deformation in the southeast of China. Journal of Seismology , 2009, 13(2): 241-252. DOI:10.1007/s10950-008-9124-0 |
| [22] | Zhang Z J, Wang G J, Harris J M. Multi-component wavefield simulation in viscous extensively dilatancy anisotropic media. Phys., Earth Planet. Inter. , 1999, 114(1-2): 25-38. DOI:10.1016/S0031-9201(99)00043-6 |
| [23] | Yang D H, Liu E R, Zhang Z J, et al. Finite-difference modelling in two-dimension anisotropic media using a flux-corrected transport technique. Geophys. J. Int. , 2002, 148(2): 320-328. |
| [24] | Yang D H, Wang S Q, Zhang Z J, et al. N-times absorbing bounding conditions for compact finite-difference modeling of acoustic and elastic wave propagation in the 2D TI medium. Bull. Seismol. Soc. Am. , 2003, 93(6): 2389-2401. DOI:10.1785/0120020224 |
| [25] | Yang D H, Zhang Z J. Poroelastic wave equation including the Biot/Squirt mechanism and the solid/fluid coupling anisotropy. Wave Motion , 2002, 35(3): 223-245. DOI:10.1016/S0165-2125(01)00106-8 |
| [26] | Zheng H S, Zhang Z J, Liu E R. Non-linear seismic wave propagation in anisotropic media using the flux-corrected transport technique. Geophysical Journal International , 2006, 165(3): 943-956. DOI:10.1111/gji.2006.165.issue-3 |
| [27] | Yang D H, Zhang Z J. Effects of the Biot and the squirt-flow coupling interaction on anisotropic elastic waves. Chinese Science Bulletin , 2000, 45(23): 2130-2138. DOI:10.1007/BF02886316 |
| [28] | Lan H Q, Zhang Z J. Seismic wavefield modeling in media with fluid-filled fractures and surface topography. Applied Geophysics , 2012, 9(3): 301-312. DOI:10.1007/s11770-012-0341-5 |
| [29] | 徐涛, 徐果明, 高尔根, 等. 三维复杂介质的块状建模和试射射线追踪. 地球物理学报 , 2004, 47(6): 1118–1126. Xu T, Xu G M, Gao E G, et al. Block modeling and shooting ray tracing in complex 3-D media. Chinese J. Geophys. (in Chinese) , 2004, 47(6): 1118-1126. |
| [30] | Xu T, Xu G M, Gao E G, et al. Block modeling and segmentally iterative ray tracing in complex 3D media. Geophysics , 2006, 71(3): T41-T51. DOI:10.1190/1.2192948 |
| [31] | Xu T, Zhang Z J, Gao E G, et al. Segmentally iterative ray tracing in complex 2D and 3D heterogeneous block models. Bull. Seismol. Soc. Am. , 2010, 100(2): 841-850. DOI:10.1785/0120090155 |
| [32] | Liu K, Zhang Z J, Hu J F, et al. Frequency band-dependence of S-wave splitting in China mainland and its implications. Science in China (Series D) , 2001, 44(7): 659-665. DOI:10.1007/BF02875339 |
| [33] | Maultzsch S, Chapman M, Liu E R, et al. Modelling frequency-dependent seismic anisotropy in fluid-saturated rock with aligned fractures: implication of fracture size estimation from anisotropic measurements. Geophysical Prospecting , 2003, 51(5): 381-392. DOI:10.1046/j.1365-2478.2003.00386.x |
| [34] | Dvorkin J, Nur A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms. Geophysics , 1993, 58(4): 524-533. DOI:10.1190/1.1443435 |
| [35] | Tsvankin I. Anisotropic parameters and P-wave velocity for orthorhombic media. Geophysics , 1997, 62(4): 1292-1309. DOI:10.1190/1.1444231 |
 2013, Vol. 56
2013, Vol. 56