地球物理学报  2013, Vol. 56 Issue (6): 1797-1808   PDF    
引用本文
王健, 冯晓哲, 赵红梅 等. 高频频率预测方法中国区域的精细化研究. 地球物理学报, 2013, 56(6): 1797-1808, doi: 10.6038/cjg20130602.  
Wang J, Feng X Z, Zhao H M, et al. Refined study of HF frequency prediction method in China region. Chinese J. Geophys. (in Chinese), 2013, 56(6): 1797-1808, doi: 10.6038/cjg20130602.  
高频频率预测方法中国区域的精细化研究
王健 , 冯晓哲 , 赵红梅 , 付炜 , 姬生云 , 王佩     
中国电波传播研究所, 青岛 266107
收稿日期 2012-07-18, 2012-11-11 收修定稿
基金项目: 国家自然科学基金项目(40904040)和广东省联合基金重点项目(U1035002)资助
作者简介: 王健, 男, 1979年生, 2005年于中国电波传播研究所获电磁场与微波技术专业硕士学位, 主要从事工程电波传播、频谱管理方面研究工作.E-mail:wangjian@criep.com
摘要: 提出了一种适用于中国及邻近区域高频天波传播的精细化频率预测方法:该方法基于ITU-R频率预测方法体系, 在应用中国参考电离层模型的基础上, 利用1976-2006年10个电离层观测站近三个太阳活动周期电离层特征数据的统计分析结果, 充分考虑预测参量随空间位置、昼夜以及太阳活动的变化特性, 重建了E层、F1层和F2层OWF-MUF和HPF-MUF转化因子的时空映射.利用中国境内2008年1月6条链路和2012年3月9条链路的观测结果, 对本文所述方法和ITU-R建议方法进行对比分析, 对比结果显示本文所述方法较ITU-R建议方法在预测精度上有了明显的改善:MUF、OWF、HPF预测的均方误差分别降低了0.28、0.16、0.45 MHz, 最大误差降低量为0.90、0.55、1.31 MHz, 均方相对误差平均降低了4.79%、2.97%和4.91%, 最大误差降低量分别为10.14%、8.63%和11.75%.
关键词: 高频      频率预测      中国区域      精细化研究     
Refined study of HF frequency prediction method in China region
WANG Jian, FENG Xiao-Zhe, ZHAO Hong-Mei, FU Wei, JI Sheng-Yun, WANG Pei     
China Research Institute of Radiowave Propagation, Qingdao 266107, China
Abstract: A refined method of HF frequency prediction has been proposed for China and adjacent region. Based on the frequency prediction method recommended by International Telecommunication Union (ITU) and statistical analysis of ionospheric characteristic data which was observed at 10 sounding stations in recent three solar activity periods from 1976 to 2006, the new mapping of conversion factor of OWF-MUF and HPF-MUF for E layer, F1 layer and F2 layer is reconstructed. The variation owing to geographic position, diurnal cycle, and solar activity is fully taken into account. Using the systematic observation which was obtained by six circuits received in Xingxiang during January 2008 and nine circuits received in Qingdao during March 2012, the prediction error of the refined method was compared with that of the ITU-R method. The results show that the predicting accuracy is effectively improved by using the refined method: the root-mean-square error of MUF, OWF and HPF is reduced by 0.28, 0.16 and 0.45 MHz respectively, and 0.90、0.55 and 1.31 MHz at most; the relative root-mean-square error of MUF, OWF and HPF is reduced by 4.79%, 2.97% and 4.91% on the average, and 10.14%, 8.63% and 11.75% at most..
Key words: HF      Frequency prediction      China region      Refined study     
1 引言

高频频率预测是频率管理的一项重要支撑技术, 被广泛应用于军事、商业等领域, 其目标是为通信链路或网络提供优质频率, 提高通信质量.国际电信联盟(ITU)在ITU-RP.1239建议中提出了参考电离层模型[1], 并基于此, 在ITU-RP.533和ITU-R P.1240建议中给出了最低可用频率(Lowest Usable Frequency, LUF)、最高可用频率(Maximum Usable Frequency, MUF)、最优工作频率(Optimum Working Frequency, OWF)和最高可能频率(Height Probable Frequency, HPF)的预测方法[2-3], 形成了一个完整的体系.研究发现:(1)由于ITU-R参考电离层模型在形成过程中缺少中国区域数据, 应用于中国区域时, 在较低纬度地区和太阳活动高年时有明显的偏差, 特别是F2层参数[4]; (2)ITU-R所推荐的频率预测方法中的最佳可用频率、最高可能频率与最高可用频率的转换因子在E层和F1层采用了固定的统计值, F2层只分段考虑太阳活动变化、纬度变化和时间变化, 而忽略了其它相关因素, 如经度变化效应、精细化的太阳活动效应[5-9].故本文在中国区域推荐应用中国参考电离层提高MUF预测精度的基础上[10-11], 提出了OWF和HPF的预测方法精细化建议, 用于进一步提高频率预测方法在中国及其邻近区域可用频率的预测精度.

2 ITU-R建议方法分析

ITU-R建议中, 基本MUF定义为在确定时间, 收发两端间仅考虑电离层折射、反射传播的最高频率[12].E层基本MUF可通过式(1)计算得到[3]:

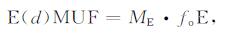
(1)

式中, d为传播路径距离, foE为路径中点处的E层临界频率, ME为转换因子, 可由式(2)和(3)计算得到:

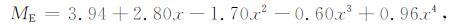
(2)

(3)

F1层基本MUF可通过式(4)计算得到[3]:

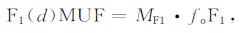
(4)

式中, foF1为路径中点处的F1层临界频率, MF1为转换因子, 可由式(5)、(6)和(7)计算得到:

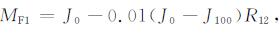
(5)

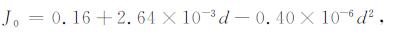
(6)

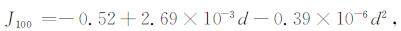
(7)

式中, R12为太阳黑子12月平均流动值.

当传播距离小于等于F2层最大跳长(dmax)时, F2层基本MUF可由式(8)计算得到[2-3]:

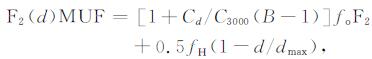
(8)

其中,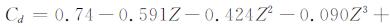

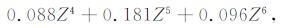
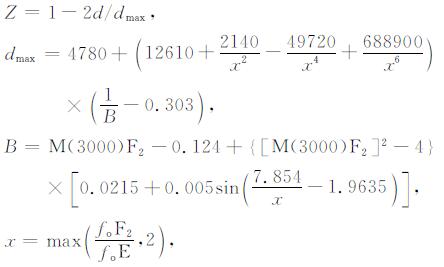
式中, C3000为3000km处的Cd值, foF2为路径中点处F2层临界频率, M(3000)F2为3000km传输因子, fH为路径中点处磁旋频率.

当传播距离大于F2层最大跳长(dmax)时, 取距收发点d0/2处F2层电离层参数, 分别按单跳情况计算基本MUF, 最后取两者较小值.

上述方法中的电离层特征参数, ITU-R建议应用ITU-RP.1239中所述方法进行计算. OWF定义为一个月内超过90%的日子里的MUF, HPF定义为一个月内超过10%的日子里的MUF[12].其中, E层、F1层、F2层OWF分别可表示为[3]

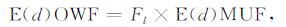
(9)

(10)

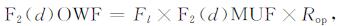
(11)

式中, E(d)MUF、F1(d)MUF和F2(d)MUF分别为E层、F1层和F2层模式在传播距离为d时的MUF, Rop为F2模式工作MUF中值与基本MUF中值的比率, Fl为OWF-MUF的转换因子, E层和F1层模式取为0.95, F2层模式如图 1所示, 是与纬度、时间和太阳活动相关的变量, 其值域范围为[0.60, 0.92].

图 1 F2层OWF与工作MUF的转换因子 Fig. 1 The conversion factor of operational MUF to OWF for F2 layer

E层、F1层、F2层HPF分别可表示为[3]

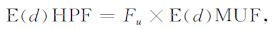
(12)

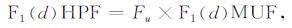
(13)

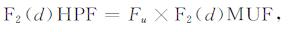
(14)

式中, Fu为HPF-MUF的转换因子, E层、F1层模1798式取为1.05, F2层模式如图 2所示, 变化特性与Fl相似, 值域范围为[1.11, 1.48].

图 2 F2层HPF与工作MUF的转换因子 Fig. 2 The conversion factor of operational MUF to HPF for F2 layer

分析上述预测方法可知:(1)E层和F1层OWF-MUF和HPF-MUF的转换因子采用了典型统计值; (2)F2层OWF-MUF和HPF-MUF的转换因子考虑了纬度、昼夜、季节和粗粒度太阳活动效应.

3 频率预测方法精细化 3.1 MUF预测中国参考电离层的引入

ITU-R建议的频率预测体系中推荐ITU-RP. 1239所述的电离层模型, 该模型后被纳入国际参考电离层(IRI)[1, 13].由于ITU-R参考电离层模型在形成过程中缺少中国区域数据, 应用于中国区域时, 在较低纬度地区和太阳活动高年时有明显的偏差[4].中国参考电离层(CRI)是依据中国及周边国家电离层大量实测资料的统计分析而得出的, 该模型与ITU-R参考模型在频率预测应用中的主要区别在于:(1)建立了适用于中国及周边地区(65°N-40°S, 60°E-150°E)的F2层参数的预测方法[4, 14-15]; (2)修改了中国区域F1出现概率[4].基于两种模型的MUF预测结果对比分析显示:两种方法同样存在着与观测结果类似的趋势, 但基于CRI的预测结果明显优于基于ITU-R参考模型的预测结果[10-11].所以, 在中国区域内, 推荐使用CRI以用于提高MUF预测精度.

3.2 OWF和HPF预测转换因子的重建

分析可知, MUF与临界频率直接相关, 进而可判定OWF和HPF的变化与临界频率严格相关, ITU-RP.1240中正是利用foF2(90%)/foF2(50%)和foF2(10%)/foF2(50%)来确定F2层的Fl和Fu.为精细化OWF-MUF和HPF-MUF的转换因子, 基于观测数据分别统计得出foE、foF1、foF2的上十分值、下十分值与中值的关系, 进而确定OWF-MUF和HPF-MUF的转换因子Fl和Fu.

3.2.1 观测数据分析

根据上述思路, 从1976年至2006年太阳活动近三个周期, 北京、长春、广州、海南、拉萨、兰州、满洲里、青岛、乌鲁木齐、重庆10个电离层观测站的foE、foF1、foF2观测数据(可用数据时间如表 3所列)入手, 分别统计分析其月中值、上十分值和下十分值, 得出不同站点Fl(fo(90%)/fo(50%))和Fu (fo(10%)/fo(50%))的变化特性.

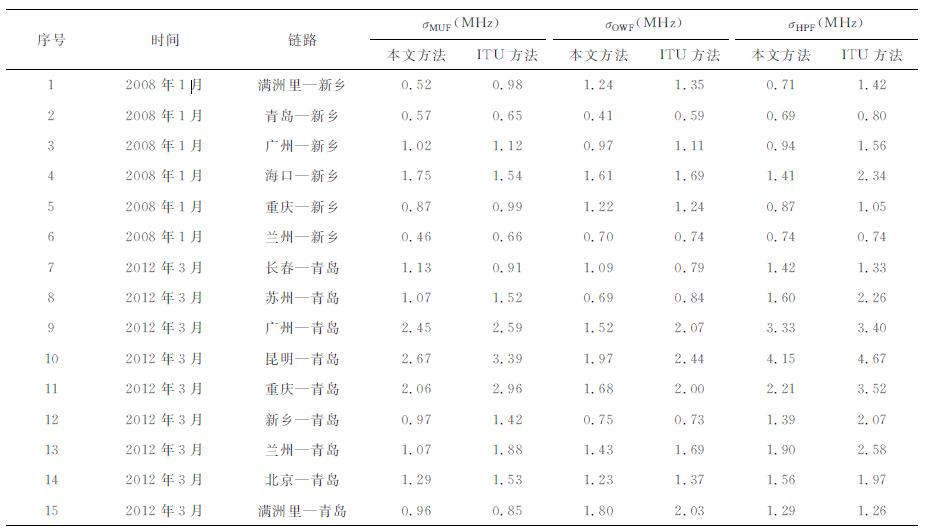
表 3 不同预测方法MUF、OWF和HPF的均方误差 Table 3 The root-mean-square error of MUF, OWF, and HPF based on two calculating methods

为去除Fl和Fu的随机噪声, 对Fl和Fu的月观测值进行12个月滑动平均处理, 即取

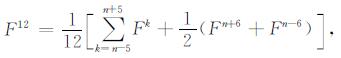
(15)

式中, Fk为Fl或Fu的月测量值.

分析10个观测站点的Fl12和Fu12, 发现:

(1) Fl12和Fu12不仅与纬度变化存在相关性, 与经度同样相关, 且不可忽略[5-8];

(2) Fl12和Fu12随太阳活动呈明显周期性变化特性, 远远超出季节的影响;

(3) F2层Fl12和Fu12的全天小时变化规律明显, E层、F1层Fl12和Fu12的全天小时变化相对稳定.

3.2.2 转换因子重建

依据上述统计结果, 考虑E层、F1层Fl和Fu全天的相关稳定性, 对其进行中值处理, 并基于此建立不同站点Fl和Fu与太阳活动参数的映射.当前, 描述太阳活动的参数有太阳黑子(R)、太阳10.7cm辐射通量(F10.7)、Ic指数、IF2指数等[1, 12-17]; 综合考虑工程的复杂度和高频频率长期预测的应用特点[1, 12, 15], 在此, 选用太阳黑子数12月平均流动值(R12), 并以R12为参量建立不同站点Fl和Fu映射:

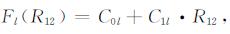
(16)

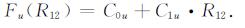
(17)

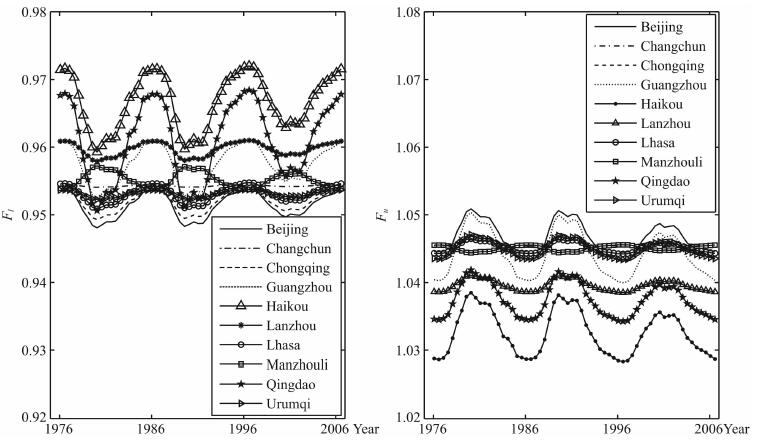
基于(16)和(17)式的映射关系, 进行回归分析, 得出E层、F1层不同站点的回归系数C0l, C1l, C0u, C1u.图 3和图 4分别给出各站点E层和F1层Fl和Fu的回归模型.

图 3 E层OWF-MUF和HPF-MUF转换因子回归模型 Fig. 3 The regression model of OWF-MUF and HPF-MUF conversion factor for E layer
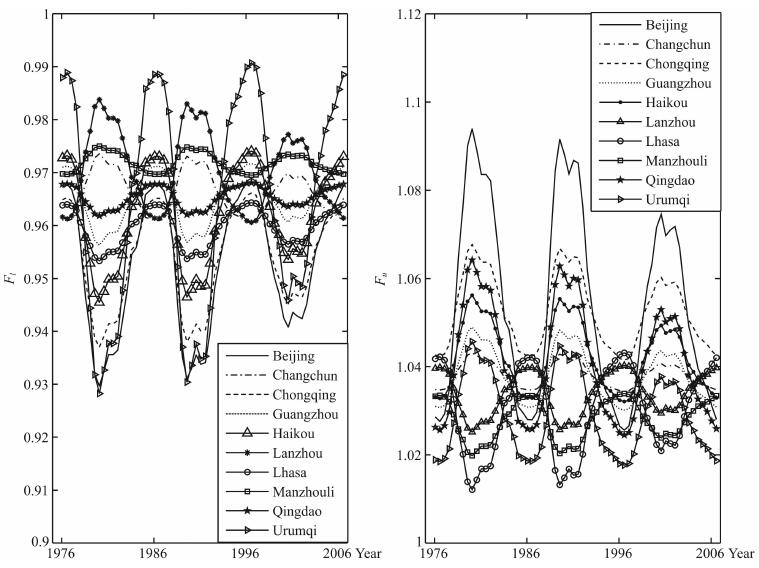
图 4 F1层OWF-MUF和HPF-MUF转换因子回归模型 Fig. 4 The regression model of OWF-MUF and HPF-MUF conversion factor for F1 layer
表 1 电离层探测站及其数据 Table 1 Data of ionosphere sounding stations

考虑F2层Fl12和Fu12全天小时变化规律明显的特点, 区别E层和F1层传播, 建立不同站点、不同时刻Fl和Fu与R12线性映射:

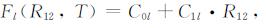
(18)

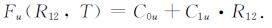
(19)

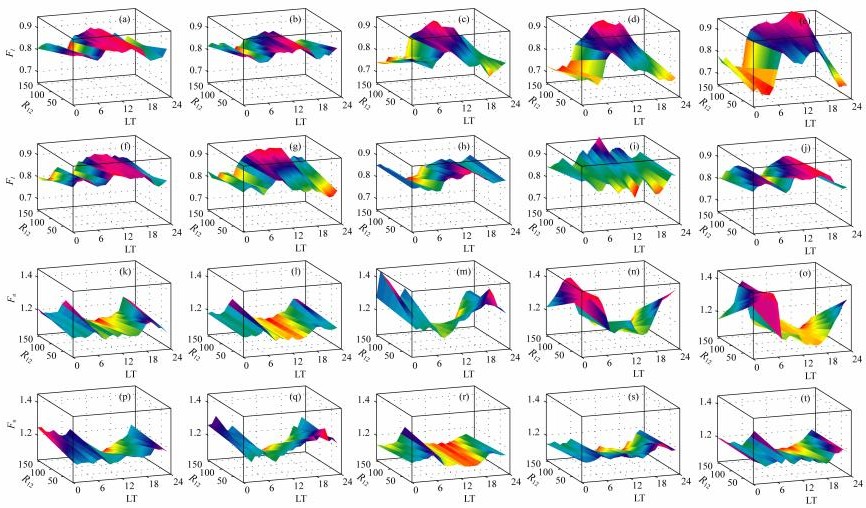
图 5给出各站点F2层Fl和Fu回归模型, 其中(a-t)分别对应北京、长春、重庆、广州、海口、拉萨、兰州、满州里、青岛、乌鲁木齐站的Fl和Fu回归模型.

图 5 F2层OWF-MUF和HPF-MUF转换因子回归模型 Fig. 5 The regression model of OWF-MUF and HPF-MUF factor for F2 layer

在上述基础上, 引入改进Kriging插值方法[18], 分别以E层、F1层、F2层的Fl和Fu六个参数为区域化变量, 建立中国及邻近地区各变量与空间、时间和太阳活动特征参数(R12)的映射关系.E层和F1层的Fl和Fu模型分别为Fl(λ, θ, R12)和Fu(λ, θ, R12), F2层Fl和Fu模型分别为Fl(λ, θ, R12, T)和Fu(λ, θ, R12, T), 其中, λ为控制点纬度, θ为控制点经度, R12为太阳黑子12月平均流动值, T为控制点当地时(0, 1, …, 23).

取某时刻F(λ, θ)作为特征变量, 已知N个观测站的F(λn, θn), n=1, 2, 3, …, N, 则区域内任一点(λ0, θ0)的Kriging估计量F(λ0, θ0)可通过如下过程求得:

(1) 定义电离层距离d, 空间任意两点(λi, θi)和(λj, θj)之间的电离层距离dij为

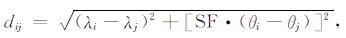
(20)

式中, SF为尺度因子, 用以考虑电离层的特性变量相关性在纬度和经度方向的差别.

(2) 利用区域重构方程组

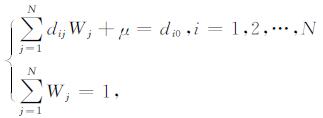
(21)

求取观测站与未知站间的权重系数W.

(3)计算未知站的Kriging估计量F(λ0, θ0),

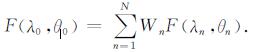
(22)

选取10个观测站中9个观测站的观测数据作为重构数据, 其中1个观测站的数据作为验证数据, 交叉分析各站F的观测值Fo(λn, θn)和Kriging估计值Fr(λn, θn)之间重构误差

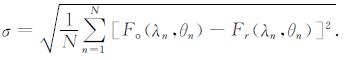
(23)

通过交叉验证, 发现:E层SF取1.3、F1层SF取2、F2层SF取1.4为最优.

图 6和图 7分别给出了太阳活动低年(R12=10)、太阳活动高年(R12=100)的中国及邻近区域E层、F1层Fl和Fu空间分布图.

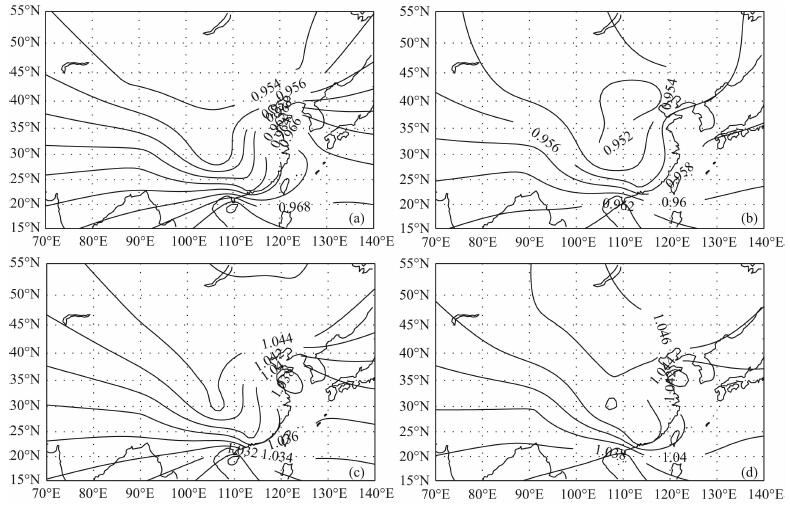
图 6 太阳活动低年和高年情况下的E层Fl和Fu空间分布 (a)Fl(R12=10);(b)Fl(R12=100);(c)Fu(R12=10);(d)Fu(R12=100). Fig. 6 The space distribution of Fl and Fu of Elayer for years of minimum and maximum solar activity
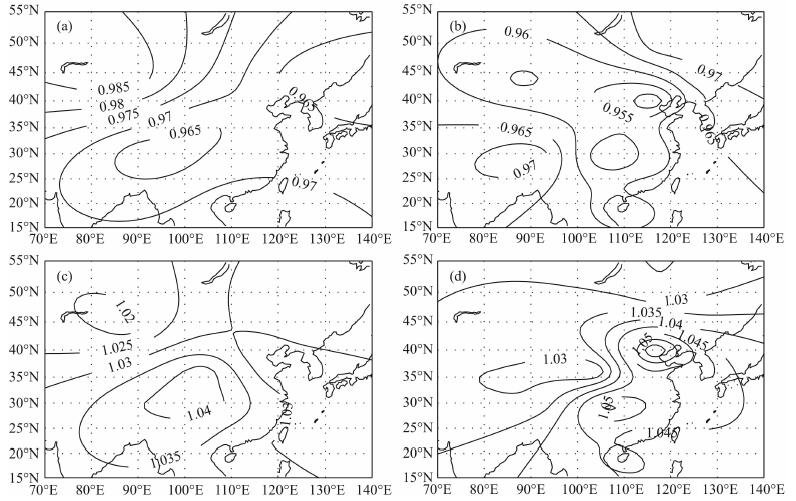
图 7 太阳活动低年和高年情况下的F1层Fl和Fu空间分布 (a)Fl(R12=10);(b)Fl(R12=100);(c)Fu(R12=10);(d)Fu(R12=100). Fig. 7 The space distribution of Fl and Fu of F1 layer for years of minimum and maximum solar activity

图 8给出太阳活动低年(R12=10)、太阳活动高年(R12=100)正午(当地时为12时)和午夜(当地时为0时)时分的中国及邻近区域F2层Fl和Fu空间趋势图.

图 8 太阳活动低年和高年情况下正午和午夜时分F2层Fl和Fu空间分布 (a)Fl(R12=10, LT=12:00);(b)Fl(R12=10, LT=00:00);(c)Fl(R12=100, LT=12:00);(d)Fl(R12=100, LT=00:00);(e)Fu(R12=10, LT=12:00);(f)Fu(R12=10, LT=00:00);(g)Fu(R12=100, LT=12:00);(h)Fu(R12=100, LT=00:00). Fig. 8 The space distribution of Fl and Fuof F2 layer for years of minimum and maximum solar activity

表 2给出了ITU-R建议方法和本文所述方法的E层、F层、F2层的Fl和Fu的值域范围; 由表 2及图 6、图 7和图 8可见:中国及其邻近区域, Fl和Fu的变化特性与ITU-R建议所述特性有明显差别.

表 2 不同预测方法值域范围对比 Table 2 Comparison of two calculating methods
4 方法评估

为评估频率预测方法的精度, 将本文方法(应用CRI和改进Fl、Fu因子)和ITU-R建议方法的MUF、OWF和HPF预测结果与2008年1月(太阳活动低年)满洲里、青岛、广州、海口、重庆、兰州-新乡6条链路(图 9a)和2012年3月(太阳活动中期)的苏州、新乡、北京、重庆、兰州、广州、长春、满洲里、昆明-青岛9条链路(图 9b)的观测结果进行对比, 分析全天24小时均方根误差

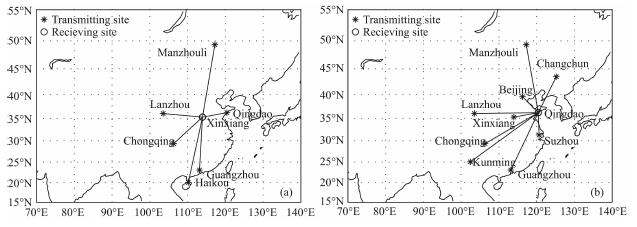
图 9 观测链路图 (a)Jan.2008;(b)Mar.2012. Fig. 9 The map of observation circut

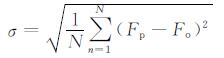
(24)

和相对均方误差

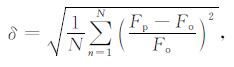
(25)

式中, Fp为MUF、OWF和HPF的预测值, Fo为MUF、OWF和HPF的观测值, N为MUF、OWF和HPF日小时统计数, 此处为24.

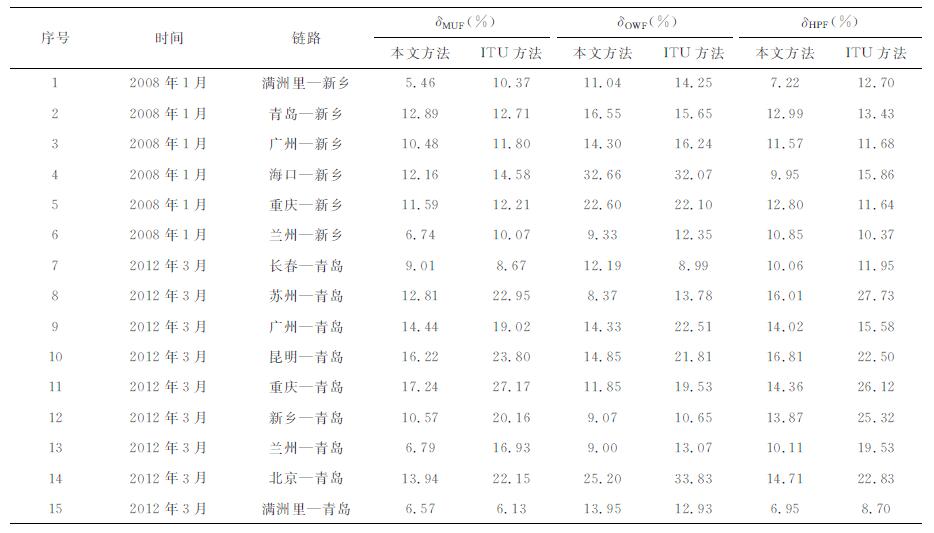
由表 3和表 4可以看出:对比ITU方法, 除少数(10%~15%)情况外, 本文方法在预测精度上有了明显的改善, MUF、OWF、HPF预测的均方误差平均减小了0.28 MHz、0.16 MHz和0.45 MHz, 最大误差减小量分别为0.90 MHz、0.55 MHz和1.31 MHz, 均方相对误差平均减小了4.79%、2.97%和4.91%, 最大误差减小量分别为10.14%、8.63%和11.75%.

表 4 不同预测方法MUF、OWF和HPF的相对均方误差 Table 4 The relative root-mean-square error of MUF, OWF, and HPF based on two calculating methods

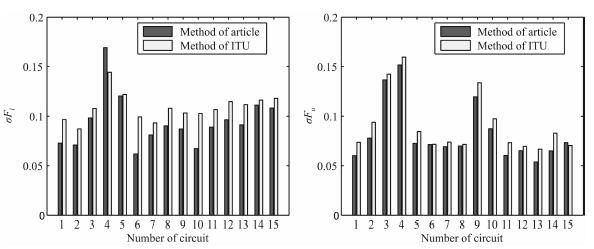
利用式(24)误差分析原理对比本文方法和ITU方法的Fl和Fu预测均方根误差σFl和σFu, 如图 10所示, 由图 10不难看出:在中国区域的大多情况本文方法有效提升了Fl和Fu预测的精度, 这也正是OWF、HPF预测精度提升的主要贡献之一.

图 10 同预测方法的Fl和Fu均方根误差 Fig. 10 The root-mean-square error of Fl and Fu based on two calculating methods
5 结论

本文针对中国区域, 对ITU所推荐高频频率预测方法提出修正思路:在引入中国参考电离层-从根源上提高频率预测方法中电离层参数预测精度的基础上, 引入中国10个电离层探测站观测数据的统计分析结果, 并利用多维空间重构理论, 重建了E层、F1层、F2层OWF-MUF和HPF-MUF的转换因子与空间、时间和太阳活动参数的映射关系, 提高了OWF和HPF的预测精度.通过预测与实测数据对比分析, 证实:本文所提精细化思路和方法, 在中国区域, 有效提高了高频频率预测精度, 可推广至全球区域范围.文中仅采集到了太阳活动低年和太阳活动中期的中、短链路的可用数据, 为确保方法的可靠性和有效性, 在进一步的深入研究中, 还需对太阳活动高年和远距离传播链路情况进行采集和对比分析.

致谢

本文所用电离层探测数据由中国电波传播研究所数据中心提供, 在此表示衷心感谢.

参考文献
[1] International Telecommunication Union. Rec P.1239-2 ITU-R reference ionospheric characteristics. Geneva, 2009.
[2] International Telecommunication Union. Rec.ITU-R P.533-9 Method for the prediction of the performance of HF circuits. Geneva, 2007.
[3] International Telecommunication Union. Rec.ITU-R P.1240-1 ITU-R methods of basic MUF, operational MUF and ray-path prediction. Geneva, 2007.
[4] 刘瑞源, 权坤海, 戴开良, 等. 国际参考电离层用于中国地区时的修正计算方法. 地球物理学报 , 1994, 37(4): 422–432. Liu R Y, Quan K H, Dai K L, et al. A corrected method of the international reference ionosphere to be used in Chinese region. Chinese. J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1994, 37(4): 422-432.
[5] Zhang S R, Coster A J, Holt J, et al. Ionospheric longitudinal variations at midlatitudes: Incoherent scatter radar observation at Millstone Hill. Sci. China Tech. Sci , 2012, 55(5): 1153-1160. DOI:10.1007/s11431-012-4784-y
[6] Mu W F, Wan W X, Ren Z P, et al. Correlation between ionospheric longitudinal harmonic components and upper atmospheric tides. Chinese Sci. Bull , 2010, 55(35): 4037-4045. DOI:10.1007/s11434-010-4205-1
[7] Li G, Ning B, Liu L, et al. The correlation of longitudinal/seasonal variations of evening equatorial pre-reversal drift and of plasma bubbles. Ann. Geophys , 2007, 25: 2571-2578.
[8] 吴健, 权坤海, 曹忠慧, 等. 中纬度观测的电离层F区经度效应及其模式计算. 空间科学学报 , 1998, 18(2): 132–140. Wu J, Quan K H, Cao Z H, et al. Observations of the longitude effects in the mid-latitude ionospheric F-region and comparisons with models. Chin. J. Space Sci. (in Chinese) , 1998, 18(2): 132-140.
[9] Liu L B, Wan W X, Chen Y D, et al. Solar activity effects of the ionosphere: A brief review. Chinese Sci. Bull , 2011, 56(12): 1202-1211. DOI:10.1007/s11434-010-4226-9
[10] Wang J, Feng X Z, Cheng L. Basic MUF observation and comparison of HF radio frequency prediction based on different ionosphere models. The 9th International Symposium on Antennas, Propagation, and EM Theory, Guangzhou, Nov.29-Dec.2, 2010. http://ieeexplore.ieee.org/document/5696486/
[11] Wang J, Zhao H M, Fu W. Further comparison of basic MUF prediction based on different ionosphere models during medium solar activity epochs. The 10th International Symposium on Antennas, Propagation, and EM Theory, Xi'an, Oct.22-Oct.26, 2012. http://ieeexplore.ieee.org/document/6408817/
[12] Rec.ITU-R P.373-1 Definitions of maximum and minimum transmission frequences. Geneva, 2007.
[13] Billtza D, Rawer K, Bossy L, et al. International reference ionosphere 1990. NSSDC/WDC-A-R & S , 1990.
[14] 孙宪儒. 亚大地区F2电离层预测方法. 通信学报 , 1987, 8(6): 37–45. Sun X R. A method of predicting the ionospheric F2 layer in the Asia Oceania region. J. Commun. (in Chinese) , 1987, 8(6): 37-45.
[15] 曹红艳, 孙宪儒. 新版亚大地区F2层电离层频率预测方法. 空间科学学报 , 2009, 29(5): 502–507. Cao H Y, Sun X R. A new method of predicting the ionospheric F2 layer in the Asia Oceania Region. Chin. J. Space Sci. (in Chinese) , 2009, 29(5): 502-507.
[16] Liu L B, Wan W X, Ning B Q. Statistical modeling of ionospheric foF2 over Wuhan. Radio Sci , 2004, 39(2).
[17] Liu R Y, Smith P A, King J W. A new solar index which leads to improved foF2 predictions using the CCIR Atlas. Telecomm J , 1983, 50(8): 408-414.
[18] 刘瑞源, 刘国华, 吴健, 等. 中国地区电离层foF2重构方法及其在短期预报中的应用. 地球物理学报 , 2008, 51(2): 300–306. Liu R Y, Liu G H, Wu J, et al. Ionospheric foF2 reconstruction and its application to the short-term forcasting in China region. Chinese J. Geophys. (in Chinese) , 2008, 51(2): 300-306.