近年来,随着计算机技术的快速发展,大地电磁测深法(MT)这种20世纪50年代初期提出的地球物理勘探方法在基础理论、资料处理解释以及仪器设备等方面都取得了长足的进步.然而,MT处理解释方法还存在许多难题没有解决,如MT三维解释还不完善,对于复杂三维地质构造的精确解释仍处于发展探索阶段.对于复杂三维地质构造而言,一种值得研究的解决方法是把它看作由地表局部三维构造和地下深部三维构造两部分组成,地球物理勘探的目标体一般是深部三维构造.这种情况下,研究表层三维构造MT响应特征,把它看作一种地质噪声加以除掉,无疑可以突显深部勘探体的响应信号,提高三维MT勘探精度.
大地电磁勘探中,近地表局部非均匀电导率分布使下置区域电导率构造引起的电磁响应发生畸变,随着大地电磁信号周期增加,局部近地表构造的影响逐渐衰减,最终与区域电导率构造产生的感应响应相比变得可以忽略[1].区域电流经过近地表非均匀构造时会发生畸变,如果这种畸变不太严重,所观测的磁场水平分量接近区域磁场水平分量,电磁场畸变主要归于电场畸变,这种畸变主要由区域电流经过近地表非均匀构造时在其边界上形成的累积电荷引起.这类畸变不但可以在大地电磁勘探中观测到,还可以发生在直流电阻率法(DC)和可控源电磁法(CSEM)中.
对于电场畸变的进一步分析会发现,虽然观测电场的幅度被近地表非均匀体严重畸变,但是电场和磁场向量之间的相位关系实质上并未受这种畸变的太大影响,相位张量与近地表非均匀体不存在时相比差别不大,大地电磁畸变分析就是要从发生畸变的观测数据中恢复区域信息.以往,对于近地表非均匀构造影响的研究多集中于近地表为三维,区域是一维或二维这种构造[2-14].这时,区域电磁场水平分量之间振幅和相位关系可以用具有两个分量成分的阻抗张量表示,而对于更为普遍、一般的三维/三维构造(近地表非均匀构造和区域构造均为三维),这种畸变影响研究甚少.本文将论证,在三维/三维构造下,可以根据观测阻抗张量计算相位张量,消除近地表非均匀构造畸变影响,恢复区域构造信息.
2 大地电磁相位张量基本理论
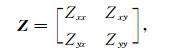
|
(1) |
利用(2)(3)式确定阻抗张量分量,表示电磁场分量之间具有线性关系:
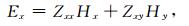
|
(2) |
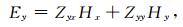
|
(3) |
阻抗张量Zxx和Zxy表达式为:
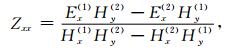
|
(4) |
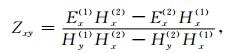
|
(5) |
式中,1和2表示大地电磁两种极化方式.相类似,利用式(3),阻抗张量分量Zyx和Zyy可以表示为:
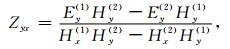
|
(6) |
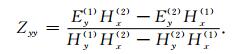
|
(7) |
这里需要注意,阻抗张量分量是复数函数,分解为实部和虚部,有以下公式:
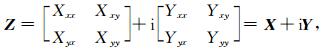
|
(8) |
其中,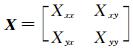
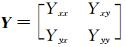
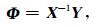
|
(9) |
其中,X-1是X的逆.注意,Φ的分量是实函数.在给定的笛卡儿坐标系(x,y)中,相位张量矩阵可以表示为:
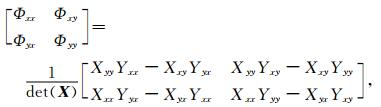
|
(10) |
其中,det(X)为X的矩阵行列式.
3 积分方程多网格法 3.1 基本原理积分方程法(IE)是电磁数值模拟与反演的有力工具[20-21],这种方法基于麦克斯韦方程组简化为关于异常体内过载电流je的积分方程组.积分方程法可以有效应用于大地电磁数值模拟,背景模型为层状电导率分布σb,异常体电导率为σa(r)=σb + Δσ(r).
这种模型中电磁场可以表示为背景场和异常场之和:
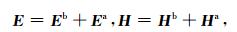
|
(11) |
其中,背景场是由给定的场源在背景电导率分布σb中产生,而异常场由异常电导率分布感应电流产生.由此,电磁场可由下列积分表达式获得:
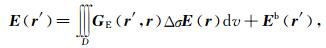
|
(12) |
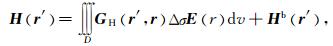
|
(13) |
式中,GE和GH分别为电、磁格林张量,在均匀构造中满足亥姆霍兹方程组:
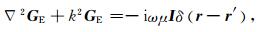
|
(14) |
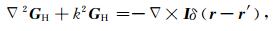
|
(15) |
式中,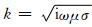
为了加快三维电磁计算速度、提高资料处理效率,同时保持一定解释精度,十几年来,人们发展了多种不同程度Born近似方法[22-23],如扩展Born近似法[24]、似线性近似(QL)、似解析近似(QA)[25-26]等.本文在QL基础上,采用了多网格方法,处理方法是:利用粗网格和细网格分别剖分模型.正演数值模拟分两步:第一步在粗网格基础上应用严格积分方程法确定电磁场,继而利用该积分方程法模拟结果计算电反射张量;第二步对由粗网格计算的电反射张量进行插值,在细网格基础上利用QL方法计算电磁场.试验证明,这种技术可以大大加快计算过程,同时保持数值模拟的计算精度.
在QL方法中,我们可以把异常体电导率看作某种已知背景电导率分布上的一种扰动.这种情况下,电磁问题的解包含两部分:(1)线性部分,非均匀体对源场的直接散射,不考虑散射电流之间的耦合;(2)非线性部分,由异常电导率和非均匀构造中未知散射场联合效应组成.本文所用的QL方法基于这样的假设,异常场与背景场的绝对值之间为线性比例关系[27]:
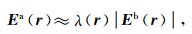
|
(16) |
其中,λ(r)=(λX,λy,λz)为电反射向量.注意,对于给定的异常和背景构造总可以找到电场电反射向量,因此(16)式总是成立.在多网格方法中,假设|Eb(rc)| ≠0(式中rc表示剖分单元位置),对于粗糙网格可以直接利用(17)-(19)式计算电反射向量的分量:
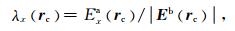
|
(17) |
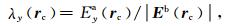
|
(18) |
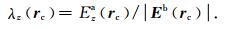
|
(19) |
得到λ(rc)后,再引入精细网格Σf描述同一模型中的电导率分布,通过线性插值可以确定新网格上的λ(rc)值.利用(20)式可以计算具有精细剖分的新网格Σf单元中心处异常电场Ea(rf),其中rf表示精细剖分单元位置:
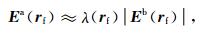
|
(20) |
计算新网格上的电场E(rf)如下:

|
(21) |
最后,对于精细网格可以利用麦克斯韦方程组积分方程的离散形式计算观测数据.
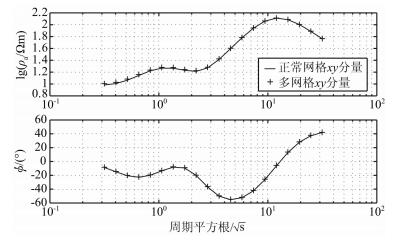
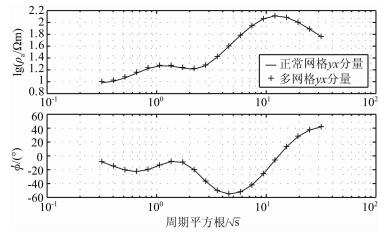
3.2 精度验证构建模型:背景构造为5层水平电阻率分布,各层电导率和厚度分别为10、1000、5、10000、20 Ωm,以及1、2、2、95 km,底层为均匀半空间.在第三层背景构造中,存在一个三维异常体,其长宽均为3 km,高度与第三层层高相同,异常体电阻率为2 Ωm.分别利用正常网格积分方程法和本文实现的多网格积分方程计算,异常体正常网格剖分单元为x、y方向均为300 m,垂直方向为200 m;粗网格剖分单元为x、y方向均为1000 m,垂直方向为500 m.接收测线位于异常体的正上方,结果如图 1、图 2所示,二者相对误差保持在3%之内.
|
图 1 视电阻率和相位xy分量积分方程正常网格和多网格计算结果比较 Fig. 1 Comparison of apparent resistivity and phase xy component computed from integral equation normal cell and coarse cell |
|
图 2 视电阻率和相位yx分量积分方程正常网格和多网格计算结果比较 Fig. 2 Comparison of apparent resistivity and phase xy component computed from integral equation normal cell and coarse cell |
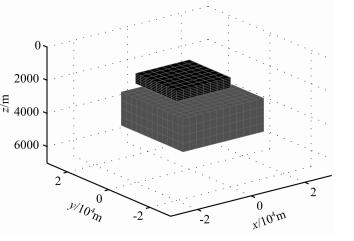
为了检验相位张量算法效果,本文选择一个具有代表性的区域大地电磁勘探模型,该模型背景构造为四层电阻率分布,以及两个立方状异常体.图 3是异常体三维分布图,图中上下两个异常体的水平尺度分别为20 km×20 km和30 km×30 km.两个异常体水平位置分别为:上异常体分别沿x、y向自-20 km开始至0 km止;下异常体分别沿x、y向自-10 km开始至20 km止.层状背景模型的电阻率自顶部起依次是10,1000,50,10000 Ωm,其下是电阻率为20 Ωm的均匀半空间,代表导电性的软流圈.背景层厚度分别为1000,2000,2000,95000 m.上边的异常体由第二层隆起形成,从而在电阻率为10 Ωm的顶层形成电阻率为1000 Ωm、600 m厚的异常.第二个异常体电阻率为2 Ωm、厚度为2000 m,位于第三层之中.数值模拟分别沿x、y向,自-30 km开始至30 km止,以间隔5 km布设接收器,共169个,共接收四个电磁场水平分量Ex,Ey,Hx,Hy.所记录的频率等对数间隔分布于0.001和10 Hz之间.
|
图 3 真实异常体电阻率3D分布图 Fig. 3 3D resistivity distribution of true anomalous bodies |
根据IE原则,剖分单元区域分为两个,分别对应上下异常体.上异常体的初始网格剖分单元水平尺度沿x、y方向均为2.5 km,垂直方向为50 m;下异常体初始网格剖分单元水平尺度沿x、y方向均为2.5 km,垂直方向为250 m.则上异常体被剖分为768个单元(8×8×12),下异常体被剖分为1152个单元(12×12×8).上异常体的粗网格剖分单元水平尺度沿x、y方向均为5 km,垂直方向为100 m;下异常体粗网格剖分单元水平尺度沿x、y方向均为5 km,垂直方向为500 m.则上异常体被剖分为96个单元(4×4×6),下异常体被剖分为144个单元(6×6×4).在CPU主频为1.5 GHz的个人电脑进行数值模拟测试,IE法计算时间约为12 min,多网格QL法的计算时间约为23 s,显著减小了数值模拟时间.对不同频率和不同测点,对比两种数值模拟结果,最大相对误差小于3%,多网格法的计算精度可以接受.
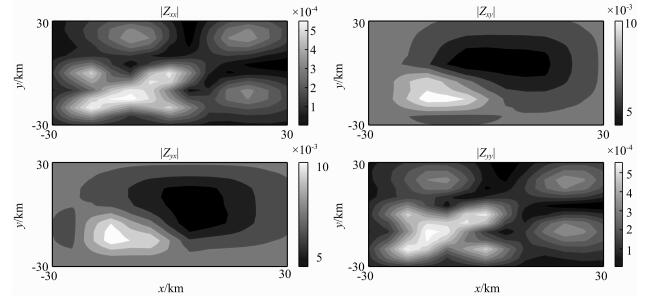
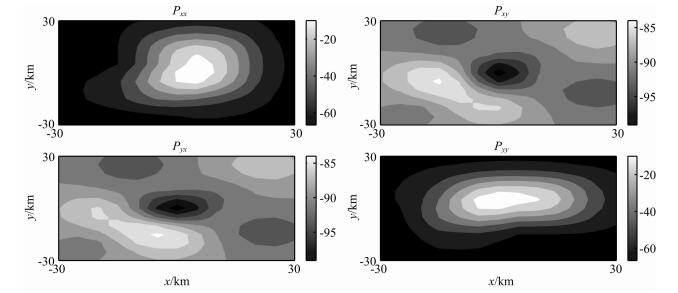
图 4是阻抗张量各分量振幅.显然,对于这种一般三维电阻率分布模型,阻抗张量分量|Zxy|和|Zyx|能够正确反映地下两个异常体的信息.|Zxy|和|Zyx|图中右上区块反映了下异常体的感应信号,左下区块则反映上异常体二次感应信号.图 5是相位张量各分量.可以看到,相位张量分量Pxx和Pyy也能够正确反映地下异常体的信息.Pxx和Pyy图中近似椭圆状反映下异常体感应信息,左下拉伸扭曲处则对应上异常体.相对浅部异常体,相位张量能更好反映深部区域构造信息.在0.001和10 Hz频率范围内测试了十几个频点,结果稳定,本文仅给出0.2 Hz模拟结果.
|
图 4 阻抗张量各分量振幅(频率:0.2 Hz,单位:Ωm) Fig. 4 Each component amplitude of resistivity tensor(frequency:0.2 Hz, unit: Ωm) |
|
图 5 相位张量各分量(频率:0.2 Hz,单位:°) Fig. 5 Each component of phase tensor(frequency:0.2 Hz, unit:°) |
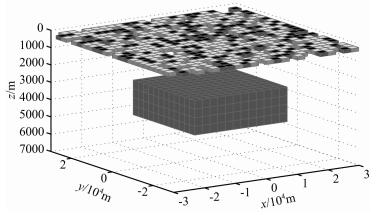
与上述模型1相似,模型2具有相同的背景电导率分布,以及同样的接收配置和频率,图 6为模型2异常体电阻率三维分布图.与模型1不同之处在于,模型2顶层中没有电阻性异常体,取而代之的是一个非均匀层,由电阻率为1,100和1000 Ωm的单元随机分布组成,单元尺寸为2500 m×2500 m× 20 m,该非均匀层模拟经常出现在勘探区域的近地表非均匀体,正是这些非均匀体引起了MT观测数据中的静位移.
|
图 6 真实异常电阻率分布三维示意图 Fig. 6 3D figure of true anomalous resistivity distribution |
剖分单元区域分为两个,分别对应上下异常体.上异常体为顶层非均匀分布,剖分单元水平尺度沿x、y方向均为500 m,垂直方向为5m.与上异常体组成单元相比,其剖分单元已经较大,不再考虑粗网格近似,则上异常体被剖分为57600个单元(120× 120×4).下异常体初始网格剖分单元水平尺度沿x、y方向均为2.5 km,垂直方向为250 m,下异常体被剖分为1152个单元(12×12×8).下异常体粗网格剖分单元水平尺度沿x、y方向均为5 km,垂直方向为500 m,下异常体被剖分为144个单元(6×6×4).类似于模型1,多网格法加快计算速度的同时,保持了可以接受的数值模拟精度.
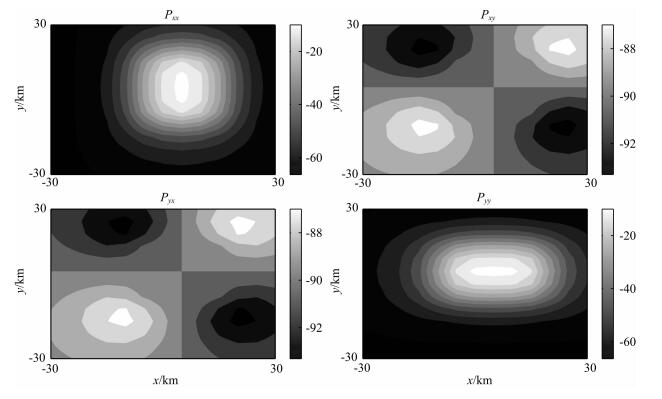
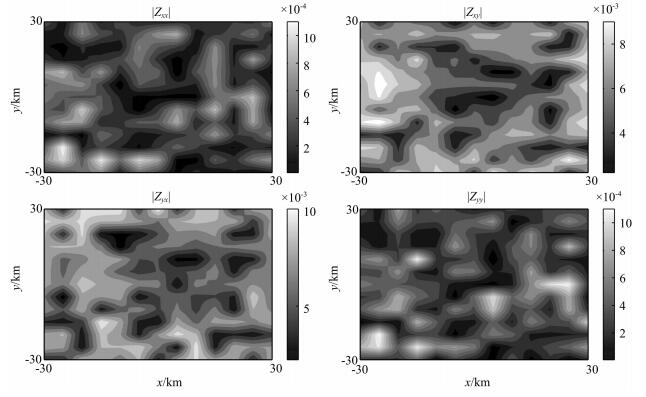
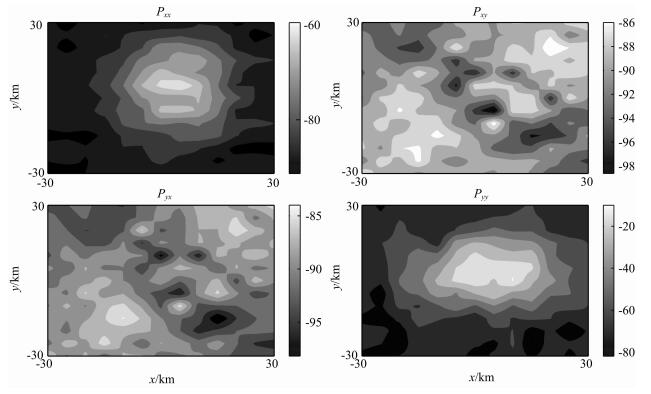
图 7是频率为0.2 Hz时,模型中不存在地表非均匀层情况下阻抗张量各分量振幅.对于这种一般三维电阻率分布模型,与模型1相似,阻抗张量分量|Zxy|和|Zyx|能够准确反映地下异常体的信息.图 8是相位张量各分量.可以看到,相位张量分量Pxx和Pyy也能够正确反映地下异常信息.图 9、图 10对应地表存在非均匀分布模型2,这种模型下,阻抗张量各分量被地表异常层强烈干扰,与不存在非均匀层模型相比,已经不能够直接从|Zxy|和|Zyx|分量看到下异常信号.然而,相位张量分量Pxx和Pyy仍然能够清楚显示下异常体感应信号,虽然与非均匀层不存在时的信号比较,这两个分量信号受到表层干扰有一定的畸变.在0.001和10 Hz频率范围内测试了十几个频点,结果显示,随着频率的增加,表层三维构造对下置勘探体的影响越来越大,在0.5 Hz以上尤为明显,但是在大地电磁主要勘探频段内,相位张量分量能够清晰地反映出深部勘探体的感应信号.限于篇幅,本文仅给出0.2 Hz模拟结果.

|
图 7 没有近地表非均匀层时阻抗张量各分量振幅(频率:0.2 Hz,单位:Ωm) Fig. 7 Each component amplitude of resistivity tensor without surface nonhomogeneous layer(frequency:0.2 Hz, unit: Ωm) |
|
图 8 没有近地表非均匀层时相位张量各分量(频率:0.2 Hz,单位:°) Fig. 8 Each component of phase tensor without surface nonhomogeneous layer (frequency:0.2 Hz, unit:°) |
|
图 9 存在近地表非均匀层时阻抗张量各分量振幅(频率:0.2 Hz,单位:Ωm) Fig. 9 Each component amplitude of resistivity tensor when surface nonhomogeneous layere xisting (frequency:0.2 Hz, unit: Ωm) |
|
图 10 存在近地表非均匀层时相位张量各分量(频率:0.2 Hz,单位:°) Fig. 10 Each component of phase tensor when surface nonhomogeneous layer existing (frequency:0.2 Hz, unit:°) |
解释MT数据困难之一是来自深部的勘探目标信息被近地表非均匀电导率分布畸变,为了克服这个困难,本文研究并实现了相位张量正演数值算法.模拟结果表明,与传统的阻抗张量各分量振幅相比,本文实现的相位张量实际应用价值在于,这种方法可以有效压制地表异常电阻率分布的干扰,突出反映深部勘探体信息.尤其是,这种方法可以应用于更为一般和普遍的三维/三维地质构造(地表非均匀构造是三维,深部区域构造亦为三维),而无须像传统方法所假设的那样,深部区域为一维或二维构造,从而增加了方法的实用性.为了加快计算,减小算法对计算机内存的需求,正演算法采取了积分方程多网格技术,数值试验表明这是一种能够保持一定精度的快速有效的数值模拟技术.下一步的工作重点是,基于这种正演算法,实现三维相位张量反演技术.根据相位张量正演结果初步判断,对于地表构造复杂或带有地形起伏的实际勘探区域,相应的反演技术应该可以得到更可靠的区域构造.
致谢本项研究的部分工作是在美国尤他大学CEMI课题组完成,在此期间得到了Michael S. Zhdanov教授的指导和帮助,作者表示诚挚的感谢!
| [1] | Jiracek G R. Near-surface and topographic distortions in electromagnetic induction. Surv. Geophys. , 1990, 11(2-3): 163-203. DOI:10.1007/BF01901659 |
| [2] | Bruton P. Analysis of broadband magnetotelluric data and an application to the Irish Variscides. Galway: National University of Ireland, 1994 . |
| [3] | Smith J T. Understanding telluric distortion matrices. Geophys. J. Int. , 1995, 122(1): 219-226. DOI:10.1111/gji.1995.122.issue-1 |
| [4] | 魏胜, 王家映, 罗志琼.全MT张量阻抗分解及其应用.//应用地球物理学进展.武汉:中国地质大学出版社, 1998:38-45. Wei S, Wang J Y, Luo Z Q. Full MT impedance tensor separation and its application.//Applied Geophysics Advance (in Chinese). Wuhan:China University of Geosciences Press, 1998:38-45. http://www.oalib.com/references/18987092 |
| [5] | 王书明. 表面局部三维大地电磁曲线畸变校正:MT畸变校正阻抗张量分解技术. 西北地震学报 , 1998, 20(4): 1–11. Wang S M. The correction of magnetotelluric curve distortion caused by surficial local three-dimension inhomogeneities:the impedance tensor decomposition technique for the correction of MT curves distortion. Northwestern Seismological Journal (in Chinese) , 1998, 20(4): 1-11. |
| [6] | 晋光文, 孙洁, 王继军. 大地电磁(MT)阻抗张量的正则分解及其初步应用. 地震地质 , 1998, 20(3): 243–249. Jin G W, Sun J, Wang J J. Canonical decomposition of the magnetotelluric (MT) impedance tensor and its preliminary application. Seismology and Geology (in Chinese) , 1998, 20(3): 243-249. |
| [7] | 赵国泽, 汤吉, 刘铁胜, 等. 山西阳高-河北容城剖面大地电磁资料的初步解释--阻抗张量分解技术及其应用. 地震地质 , 1996, 18(1): 66–74. Zhao G Z, Tang J, Liu T S, et al. Preliminary interpretation of MT data along profile from Yanggao to Rongcheng:application of decomposition of MT impedance tenso. Seismology and Geology (in Chinese) , 1996, 18(1): 66-74. |
| [8] | Ritter P. Separation of local and regional information in geomagnetic response functions using hypothetical event analysis. Edinburgh: University of Edinburgh, 1996 . |
| [9] | McNeice G W, Jones A G. Multisite, multifrequency tensor decomposition of magnetotelluric data. Geophysics , 2001, 66(1): 158-173. DOI:10.1190/1.1444891 |
| [10] | 晋光文, 孔祥儒. 大地电磁阻抗张量的畸变与分解. 北京: 地震出版社, 2006 . Jin G W, Kong X R. MT Impedance Distortion and Separation (in Chinese). Beijing: Seismological Press, 2006 . |
| [11] | 李洋, 于鹏, 张罗磊, 等. 基于混合优化算法的MT阻抗张量畸变分解方法. 地球物理学报 , 2010, 53(8): 1924–1930. Li Y, Yu P, Zhang L L, et al. MT distortion decomposition of magnetotelluric impedance tensor based on hybrid optimization algorithm. Chinese J. Geophys. (in Chinese) , 2010, 53(8): 1924-1930. |
| [12] | 蔡军涛, 陈小斌, 赵国泽. 大地电磁资料精细处理和二维反演解释技术研究(一)--阻抗张量分解与构造维性分析. 地球物理学报 , 2010, 53(10): 2516–2526. Cai J T, Chen X B, Zhao G Z. Refined techniques for data processing and two-dimensional inversion in magnetotelluricⅠ: tensor decomposition and dimensionality analysis. Chinese J. Geophys. (in Chinese) , 2010, 53(10): 2516-2526. |
| [13] | 杨长福, 林长佑, 徐世浙. 大地电磁GB张量分解法的改进. 地球物理学报 , 2002, 45(Suppl): 356–364. Yang C F, Lin C Y, Xu S Z. The improvement of the Groom-Baily's tensor decomposition in magnetotellurics. Chinese J. Geophys. (in Chinese) , 2002, 45(Suppl): 356-364. |
| [14] | 王立凤, 晋光文, 孙洁, 等. 一种简单的大地电磁阻抗张量畸变分解方法. 西北地震学报 , 2001, 23(2): 172–180. Wang L F, Jin G W, Sun J, et al. A simple decomposition method of distortion in magnetotelluric impedance tensor. Northwestern Seismological Journal (in Chinese) , 2001, 23(2): 172-180. |
| [15] | Berdichevsky M N, Dmitriev V L, Keller G V. Magnetotellurics in the Context of the Theory of Ill-Posed Problems. Frank: Society of Exploration Geophysicists, 2002 . |
| [16] | Berdichevsky M N, Dmitriev V I. Models and Methods of Magnetotellurics. Berlin: Springer-Verlag, 2008 . |
| [17] | 陈乐寿, 刘任, 王天生. 大地电磁测深资料处理与解释. 北京: 石油工业出版社, 1989 . Chen L S, Liu R, Wang T S. Magnetotelluric Data Processing and Interpretation (in Chinese). Beijing: Oil Industry Press, 1989 . |
| [18] | 陈乐寿, 王光锷. 大地电磁测深法. 北京: 地质出版社, 1990 . Chen L S, Wang G E. Magnetotelluric Sounding (in Chinese). Beijing: Geological Publishing House, 1990 . |
| [19] | Caldwell T G, Bibby H M, Brown C. The magnetotelluric phase tensor. Geophys. J. Int. , 2004, 158(2): 457-469. DOI:10.1111/gji.2004.158.issue-2 |
| [20] | Weidelt P. Inversion of two-dimensional conductivity structures. Physics of the Earth and Planetary Interiors , 1975, 10(3): 282-291. DOI:10.1016/0031-9201(75)90054-0 |
| [21] | Homann G W. Three-dimensional induced polarization and electromagnetic modeling. Geophysics , 1975, 40(2): 301-324. |
| [22] | Born M. Optics. Berlin: Springer, 1933 . |
| [23] | Born M, Wolf E. Principles of Optics. (6th ed). New York: Pergamon Press, 1980 . |
| [24] | Habasy T M, Groom R W, Spies B R. Beyond the Born and Rytov approximations:a nonlinear approach to electromagnetic scattering. J. Geophys. Res. , 1993, 98(B2): 1759-1775. DOI:10.1029/92JB02324 |
| [25] | Zhdanov M S, Fang S. Quasi-linear approximation in 3-D electromagnetic modeling. Geophysics , 1996, 61(3): 646-665. DOI:10.1190/1.1443994 |
| [26] | Zhdanov M S. Geophysical Inverse Theory and Regularization Problems. Amsterdam: Elsevier, 2002 . |
| [27] | Fang S, Atlas B, Gao G Z, et al. Fast 3D modeling of borehole induction measurements in dipping and anisotropic formations using a novel approximation technique. Petrophysics , 2004, 45(4): 335-349. |
 2013, Vol. 56
2013, Vol. 56

