海相碳酸盐岩储层富含油气资源,油气产量占世界总产量60%左右,在我国的四川盆地、塔里木盆地、鄂尔多斯盆地、渤海和南海珠江口等多个探区先后发现了不同时代、类型和特征的大型碳酸盐岩油气田,勘探潜力巨大[1-2].碳酸盐岩地层沉积和成岩演化的特殊性和复杂性,使得其储集空间多呈现出孔隙、孔洞、裂缝及其相互组合,表现为如下主要特征:①储层内部岩性和孔隙流体结构的非均质性强;②岩性横向变化剧烈;③速度空间变化大,从而造成地震资料绕射波发育、波组连续性差[3-4],为此传统以一次反射波为主要研究对象的成像方法难以实现对碳酸盐岩储层的精确成像.
碳酸盐岩储层研究主要集中在储层特征及成像两个方面.首先,对碳酸盐岩储层特征及形成机理的研究,一直是地球物理学家们研究的热点问题.2009年刘立峰等[5]利用优化后的综合预测属性,可精细刻画碳酸盐岩缝洞型储层的空间分布规律.通过孔洞物理模型试验及其地震响应特征分析,探究了碳酸盐岩储层等效地震地质模型的地震波响应特征[1, 6-8];通过弹性波有限差分正演技术、偏移成像处理、属性反演,揭示了碳酸盐岩储层形成串珠状构造的机理[3, 8-9].基于碳酸盐岩储层AVO响应特征进行流体识别的技术[10]以及盐下碳酸盐岩储层礁体识别技术[11].
其次,围绕碳酸盐岩储层的成像技术,许多学者进行了大量的研究工作.Kozlov等[12],Moser等[13]分别通过修改Kirchhoff叠前深度偏移积分公式中的加权函数,在成像过程中压制反射、突出保持绕射能量;依据反射和绕射能量在共偏移距道集、共炮道集、合成平面波道集等不同叠前道集以及局部成像矩阵道集上的时差、波形、能量分布等特征差异,利用倾角滤波[14]、反射聚焦[13, 15]、加权Radon变换[16]、平面波解构滤波[17-19]、奇异值分解[20]等波场分离方法,提取绕射能量,提高散射目标体的成像精度;朱生旺等[21]利用倾角分解方法压制共散射点道集相干噪声以改善碳酸盐岩的绕射波成像分辨率;Cohen和Bleistein[22]以小扰动近似和Born近似为理论基础,建立逆散射扰动反演成像方法;Tarantola、Mora、Pratt等[23-28]分别在时间和频率域探究了修正最佳地下介质模型的最小二乘反演方法;杜正聪等[29]推导并利用Rytov近似傅里叶波场延拓算子对碳酸盐岩缝洞型储层进行正演和偏移并揭示其波场特征;卢明辉等[30]分析了频率域声波逆散射成像方法中影响碳酸盐岩溶洞成像精度的主控因素.
近年来,最小二乘算法在地震处理解释等方面,发挥了越来越重要的作用.最小二乘偏移思想由LeBras和Clayton提出[31],Lambaré[32]进行了补充和完善;随后,Nemeth[33]对方法进行了系统研究和改进.Kuehl和Sacchi[34]提出了裂步法最小二乘偏移算法;贾晓峰等[35]也提出采用滑动最小二乘窗求解波动方程.邹强等[36]采用最小二乘估计算法,实现了走时与波阻抗联合反演求取层速度的方法.采用最小平方法的数据规则化[37],数据去噪处理[38].杨其强等[39]改进了基于傅里叶有限差分算子的最小二乘偏移算法,并用于物理模型的试算,取得了较为明显的效果.黄建平等[40]实现了基于最小二乘的叠前深度偏移算法,并通过盐丘模型的试算,验证了该方法对于高速岩体下部成像的优势.
本文在前人研究的基础上,实现了叠前域最小二乘偏移算法,并对一系列不同裂缝尺度、不同裂缝倾角的碳酸盐岩裂缝型储层等效地震地质模型在不同计算主频情况下进行了偏移成像试算,进而讨论了LSM算法在不同计算条件下对模型的适应性,为我国南方海相及西部探区碳酸盐岩储层的勘探开发提供了一种较为有效的针对深部复杂构造的成像方法.
2 LSM成像原理及等效模型建立 2.1 LMS成像原理考虑含弱散射体速度模型,采用Born近似方法,可以得到接收波场D(g|s)的表达式,如等式(1)所示:
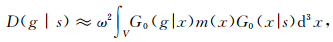
|
(1) |
其中,G0(x|s)代表从源到散射点的波场,G0(g|x)代表从散射点到接收点的格林函数,矩阵表达式为
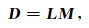
|
(2) |
其中L为线性算子.为此,模型空间的最小二乘偏移解可表示为
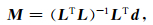
|
(3) |
对比常规偏移方法,一般假定(LTL)-1 ≈I,为此等式(3)变化为公式(4):
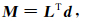
|
(4) |
其中,成像过程中的单程波算子,采用Kirchhoff成像算子mk,如公式(5):
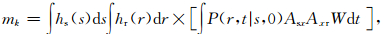
|
(5) |
其中,hs(s)和hr(r)分别为激发和采样函数;P(r,t|s,0)为地震记录矢量;Asx和Axr代表震源到散射点以及散射点到接收点输运方程的解.(3)式将简化为常规偏移方法对应的矩阵方程(4).由最小二乘偏移解表达式(3)与常规偏移解(4)对比可知,最小二乘偏移方法成像精度要优于常规偏移.
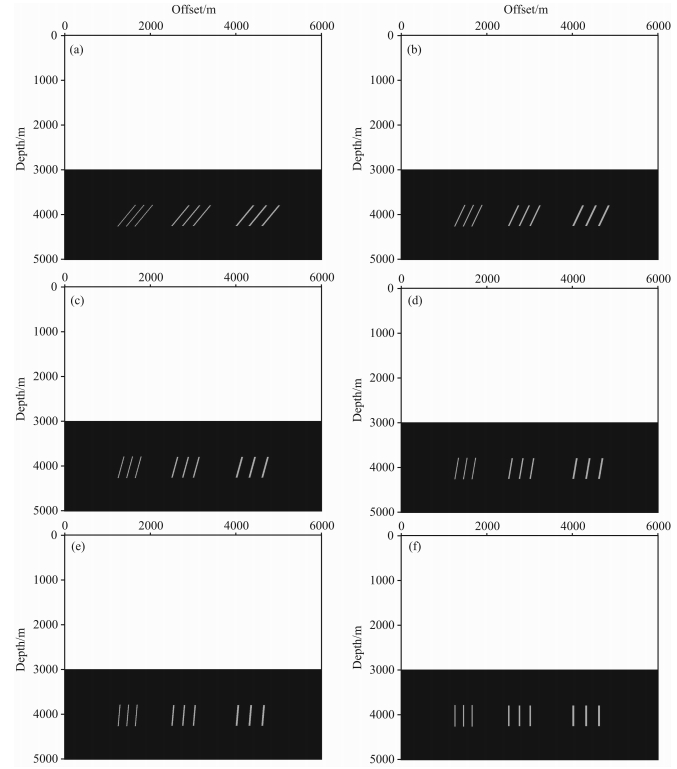
2.2 等效模型建立为了测试本文方法对中深部碳酸盐岩储层的成像分辨率,本文建立了一系列不同裂缝倾角、不同裂缝宽度的碳酸盐岩储层模型,如图 1所示.本文所建立的碳酸盐岩裂缝型储层的等效地震地质模型水平向大小为6km,深度方向为5km,上覆层厚度为3km,纵波速度为3000 m/s;下部背景围岩厚度为2.0km,纵波速度为5000 m/s;碳酸盐岩裂缝储层位于地表以下4km左右,纵波速度为3600m/s,裂缝分为三组,组内裂缝长宽尺度保持一致,为了考察不同裂缝宽度成像分辨率的差异,不同组裂缝宽度从左到右分别为20、30、40m,裂缝长度均为450m.
|
图 1 中深部碳酸盐岩不同倾角等效地震地质模型示意图 (a)倾角为30°的速度模型;(b)倾角为45°的速度模型;(c)倾角为60°的速度模型;(d)倾角为70°的速度模型;(e)倾角为80°的速度模型;(f)倾角为90°的速度模型. Fig. 1 The sketch map of the equivalent of the seism-geological carbonate velocity model at different dip angles (a) Dip angle is 30°; (b) Dip angle is 45°; (c) Dip angle is 60°; (d) Dip angle is 70°; (e) Dip angle is 80°; (f) Dip angle is 90°. |
为了测试LSM方法对中深部碳酸盐岩缝洞储集体等效地震地质模型的成像分辨率,对图 1中的模型进行了迭代次数为20的LSM成像处理,同时也计算了10Hz到50 Hz,间隔为10 Hz不同主频下的成像结果,重点测试LSM方法在不同计算条件下对中深部成像效果的差异,并总结出最优成像方案,为实际地震采集系统的设计提供理论依据.根据不同的侧重点,主要从以下三个方面展示成像结果:
3.1 不同迭代次数成像结果对比LSM是一个迭代反演成像过程,不同迭代次数下成像结果会存在较为明显的差异,随着迭代次数的增加,成像结果会逐渐收敛到其真实值.以裂缝倾角等于30°时为例,图 2给出了几种典型迭代次数下的LSM成像结果.其中图 2a为迭代第5次的成像结果,由于模型较为简单,在5次迭代时已经能够较好的分辨主要的界面及中深部的碳酸盐岩储层的分布情况,只是在某些区域能量没有较好的收敛,存在一个较为明显的能量弥散区域,同时在裂缝两个端点处,存在较为明显的尚未完全收敛的绕射波痕迹.随着迭代次数的增加,如图 2(b,c,d)所示:虚线框所示区域内能量得到较好的收敛,同时,在裂缝两侧的绕射波能量也进一步得以归位,成像分辨率逐渐提高.综上所述:当迭代次数为20次时,采用LSM成像方法能够较好地分辨地下4000 m处20 m尺度的碳酸盐岩裂缝储层,裂缝的倾角、位置、长宽尺度等空间形态得到了很好的归位,成像结果精度较高,成像分辨率达到20m尺度,较传统方法有一定的提高.
|
图 2 地质倾角等于30°时,不同迭代次数下LSM成像结果示意图 (a)LSM5次迭代成像结果;(b)LSM10次迭代成像结果;(c)LSM15次迭代成像结果;(d)LSM20次迭代成像结果. Fig. 2 The LSM imaging result at different iteration numbers with the fracture dip angle of 30° (a)LSM imaging result at iteration 5;(b)LSM imaging result at iteration 10; (c)LSM im agingresult at iteration 5;(d)LSM imaging result at iteration 10. |
从比较不同迭代次数成像结果可知,针对本文建立的碳酸盐岩储层等效地震地质模型,迭代次数为20时,能够较好地获取地下储层的空间展布.为此以20次作为成像的标准,比较不同裂缝地质倾角情况下LSM的成像结果的差异,其中裂缝倾角从30°变化到90°.
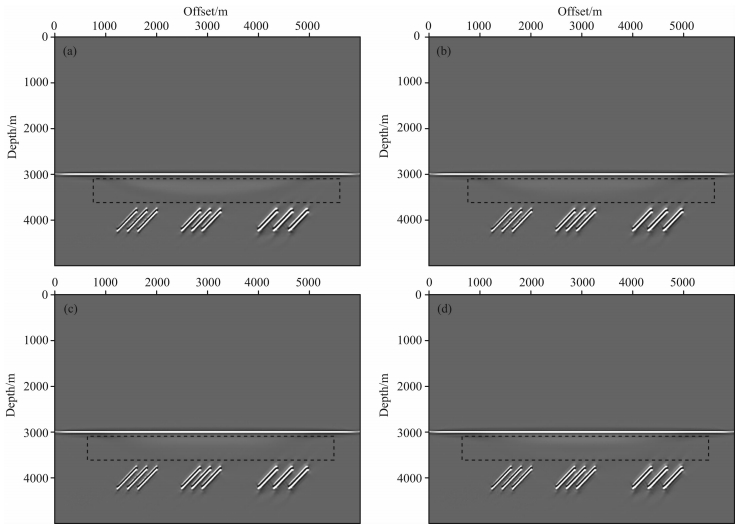
不同地质倾角情况成像结果,如图 3(a-f)所示.通过对比可以发现:当裂缝倾角为30°时,成像结果较为清晰,能够较好地分辨出20m尺度的裂缝,包括其上下边界和左右边界,随着裂缝倾角的增大,成像结果变差,尤其是裂缝的侧翼,与其它单程波方程类似,由于采样射线的缺失,成像分辨率较低,只能成像出裂缝的顶底界面.由此可见,当裂缝倾角小于70°时,LSM能够较好的刻画碳酸盐岩储层裂缝的顶底、侧翼等四个边界,而当裂缝倾角大于等于70°,LSM对裂缝顶底界面能够较好地成像,而对裂缝的侧翼成像效果不佳,需要引入双程波的逆时偏移技术,综合考虑上行和下行射线信息,以提高对裂缝侧翼的成像分辨率.

|
图 3 迭代次数为20时,不同地质倾角偏移结果对比示意图 (a)30°倾角的偏移结果;(b)45°倾角的偏移结果;(c)60°倾角的偏移结果;(d)70°倾角的偏移结果;(e)80°倾角的偏移结果;(f)90°倾角的偏移结果. Fig. 3 The sketch map of the LSM imaging result at different dip angles with the iteration number 20 (a)the imaging result at dip angle 30°; (b)the imaging result at dip angle 45°; (c)the imaging result at dip angle 60°; (d)the imaging result at dip angle 70°; (e)the imaging result at dip angle 80°; (f)the imaging result at dip angle 90°. |
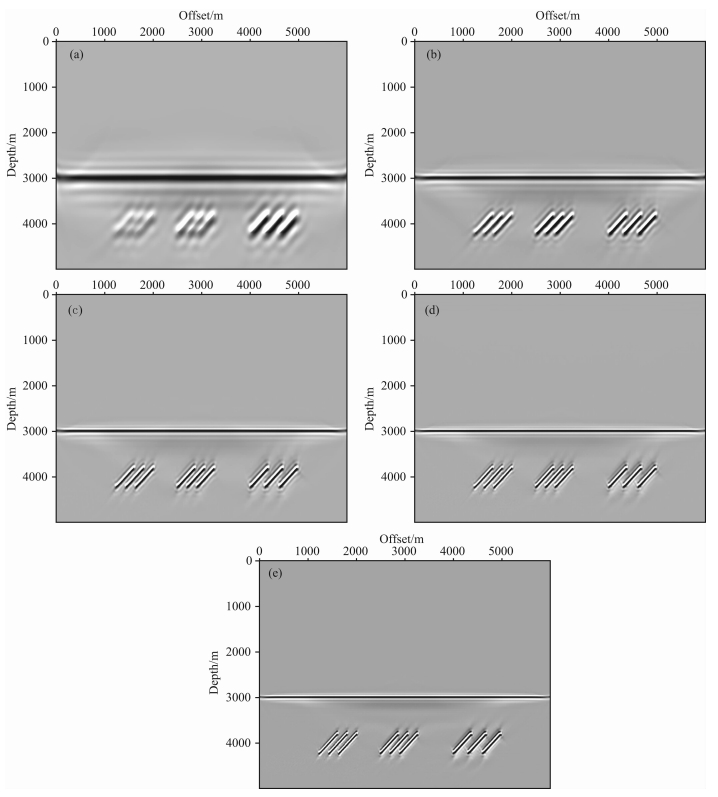
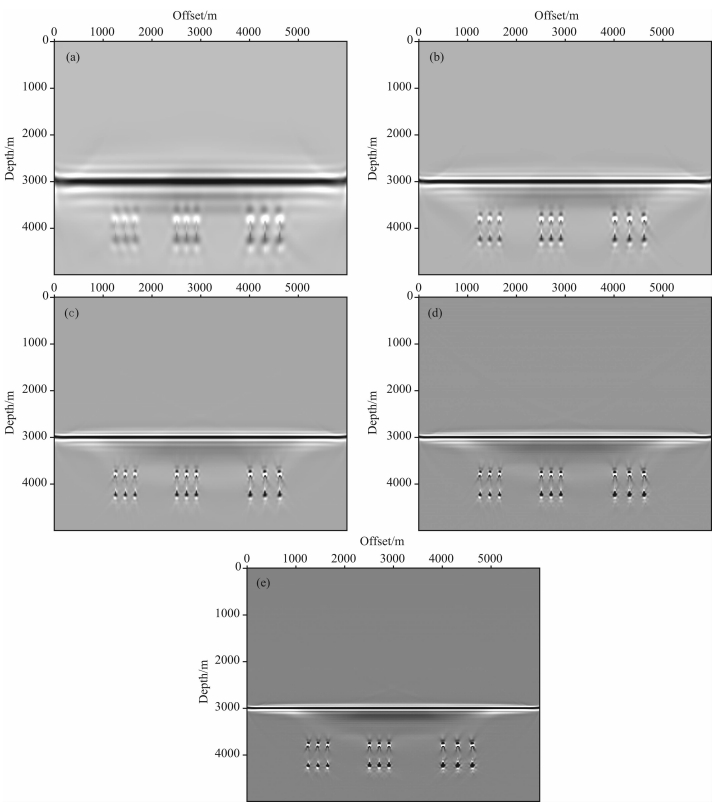
在前面研究的基础上,比较了不同计算主频下的LSM成像结果,如图 4所示,其中碳酸盐岩裂缝储层的倾角为30°,频率的变化范围为10~50 Hz,频率间隔为10 Hz.由图 4可以看出:在频率较低时,能量较为发散,成像结果较为模糊.当频率升高果的普适性,本文也给出了碳酸盐岩裂缝倾角为90°时的成像结果,如图 5所示.LSM成像结果随着频率变化的规律与裂缝倾角为30°时较为类似,也是随着频率的增加成像分辨率提高;然而,当裂缝为90°时,LSM成像方法也存在对陡倾角构造采样不足的问题,对于垂直裂缝边界的成像分辨率缺失,只能较好的刻画裂缝的上下边界的位置,需要采用基于双程波方程的逆时偏移(RTM)方法,改善对碳酸盐岩储层垂直边界的成像分辨率.由图 4和图 5的成像结果可以看出:当数据的主频在30 Hz以上时,LSM方法能够较为清晰地分辨地下4000m处得20m尺度的裂缝储层,尤其需要着重指出的是本文的成像方法也能将裂缝储层的边界较为清晰的刻画出来,这对于后续储层评价,油气储量预测具有十分重要的意义.
|
图 4 裂缝倾角为30°时,不同频率下LSM成像效果比较 (a)10Hz时的偏移结果;(b)20Hz时的偏移结果;(c)30Hz时的偏移结果;(d)40Hz时的偏移结果;(e)50Hz时的偏移结果. Fig. 4 The LSM imaging result at different do minant frequencies with the fracture dip angle 30° (a)LSM imaging result at frequency 10 Hz; (b)LSM imaging result at frequency 20 Hz; (c)LSM imaging result at frequency 30 Hz; (d)LSM imaging result at frequency 40 Hz; (e)LSM imaging result at frequency 50 Hz. |
|
图 5 裂缝倾角为90°时,不同频率下LSM成像效果比较 (a)10Hz时的偏移结果;(b)20Hz时的偏移结果;(c)30Hz时的偏移结果;(d)40Hz时的偏移结果;(e)50Hz时的偏移结果. Fig. 5 The LSM imaging result at different do minant frequencies with the fracture dip angle 90° (a)LSM imaging result at frequency 10 Hz; (b)LSM imaging result at frequency 20 Hz; (c)LSM imaging result at frequency 30 Hz; (d)LSM imaging result at frequency 40 Hz; (e)LSM imaging result at frequency 50 Hz. |
本文建立了不同地质倾角的典型碳酸盐岩裂缝等效地震地质模型,并通过LSM算法测试了不同LSM迭代次数、不同裂缝地质倾角、不同数据主频时LSM的成像结果,通过对比分析可以得到如下几点主要结论:(1)从不同迭代次数的LSM成像结果可知,随着迭代次数的增加,成像效果分辨率提高,尤其是对深度在3000 m以下的中深部碳酸盐岩储层的成像分辨率提高贡献较大.获取较为清晰的成像结果与所研究区域地质模型的复杂程度有着密切关系,在不显著增加计算量的时候,可适当选择较大的LSM迭代次数,比如30次左右,通常能够得到较为理想的成像效果,储层的边界得到了清晰的刻画;(2)从不同地质倾角的碳酸盐岩裂缝型储层的成像结果可知,LSM对于裂缝储层的地质倾角小于70°,成像结果较为清晰,裂缝顶底及左右边界刻画都较为准确清晰,当地质倾角大于70°时的高陡构造,LSM仍然能够对裂缝储层的上下边界较为清晰的成像,但是由于垂直边界采样不足,对裂缝储层的左右边界分辨率较低,此时,需要基于双程波方程的逆时偏移方法提高对裂缝垂直边界的成像能力;(3)从不同主频,LSM算法对裂缝型储层的成像分辨率受到计算主频影响较大,随着主频的提高,成像分辨率改善明显.通过大量模型测试,发现在主频30 Hz以上,LSM能够较好地对小尺度异常体成像,而对于主频较低的数据,应该结合一些拓频处理方法提高数据频宽[28, 32],然后再进行LSM成像处理.
虽然LSM对于中深部碳酸盐岩储层具有较好的成像分辨率,LSM方法还不是十分完善,也存在一些需要进一步改善的地方,比如:(1)计算效率不高,需要通过不断迭代来达到对真实数据的最佳逼近,有时还可能陷入局部极小值或者出现计算不收敛的情况[40];(2)Hessian矩阵的计算和存储方式还需要进一步优化,以满足大规模探区数据计算的需求;(3)LSM方法对地震数据的质量要求较高,在处理实际数据时,需要较高的数据品质和较好的初始速度模型;(4)本文目前的研究重在验证方法的成像效果,对于实际资料的成像处理,还需要进一步尝试.在后续的研究过程中,一方面我们将努力从上述几方面改进LSM算法,使之具有更强的适应性和更高的计算效率,另一方面,我们也要充分发挥LSM对中深部碳酸盐岩储层较好的成像能力,将LSM思想与基于GPU加速的逆时偏移技术相结合[41-43],从而更好地为我国西部碳酸盐岩探区的勘探开发服务.
致谢感谢两位匿名审稿人的宝贵意见.感谢GenericMappingTools(GMT)为本文的绘图提供的支持.
| [1] | 撒利明, 姚逢昌, 狄帮让, 等. 缝洞型储层地震识别理论与方法. 北京: 石油工业出版社, 2010 : 61 -83. Sa L M, Yao F C, Di B R, et al. Theory and methodology of the seismic identification for the Fissure-vug reservoir (in Chinese). Beijing: Petroleum Industry Press, 2010 : 61 -83. |
| [2] | 刘光鼎, 陈洁. 中国海域残留盆地油气勘探潜力分析. 地球物理学进展 , 2005, 20(4): 881–888. Liu G D, Chen J. Potential analysis of petroleum explortation in residual basins of the China Sea. Progress in Geophysics (in Chinese) , 2005, 20(4): 881-888. |
| [3] | 孙东, 潘建国, 雍学善, 等. 碳酸盐岩储层垂向长串珠形成机制. 石油地球物理勘探 , 2010, 45(Suppl.1): 101–104. Sun D, Pan J G, Yong X S, et al. Formation mechanism of vertical "long string beads" in carbonate reservoir. Oil Geophysical Prospecting (in Chinese) , 2010, 45(Suppl.1): 101-104. |
| [4] | 王彦峰, 王乃建, 高国成, 等. 缝洞型油气藏高精度三维地震采集技术. 石油地球物理勘探 , 2010, 45(Suppl.1): 1–5. Wang Y F, Wang N J, Gao G C, et al. 3D seismic acquisition technique for fracture-vuggy reservoir. Oil Geophysical Prospecting (in Chinese) , 2010, 45(Suppl.1): 1-5. |
| [5] | 刘立峰, 孙赞东, 杨海军, 等. 缝洞型碳酸盐岩储层地震属性优化方法及应用. 石油地球物理勘探 , 2009, 44(6): 747–754. Liu L F, Sun Z D, Yang H J, et al. Seismic attribute optimization method and its application for fractured-vuggy carbonate reservoir. Oil Geophysical Prospecting (in Chinese) , 2009, 44(6): 747-754. |
| [6] | 季敏, 魏建新, 王尚旭. 孔洞物理模型数据的地震响应特征分析. 石油地球物理勘探 , 2009, 44(2): 196–200. Ji M, Wei J X, Wang S X. Analysis of seismic response of pore-cave physical model data. Oil Geophysical Prospecting (in Chinese) , 2009, 44(2): 196-200. |
| [7] | 赵裕辉, 胡建中, 鲁新便, 等. 碳酸盐岩缝洞型储集体识别与体积估算. 石油地球物理勘探 , 2010, 45(5): 720–724. Zhao Y H, Hu J Z, Lu X B, et al. Identification of carbonate fractured-vuggy reservoir and volume estimation. Oil Geophysical Prospecting (in Chinese) , 2010, 45(5): 720-724. |
| [8] | 姚姚, 唐文榜. 深层碳酸盐岩岩溶风化壳洞缝型油气藏可检测性的理论研究. 石油地球物理勘探 , 2003, 38(6): 623–629. Yao Y, Tang W B. Theoretical study of detectable cavern-fractured reservoir in weathered Karst of deep carbonatite. Oil Geophysical Prospecting (in Chinese) , 2003, 38(6): 623-629. |
| [9] | 吴俊峰, 姚姚, 撒利明. 碳酸盐岩特殊孔洞型构造地震响应特征分析. 石油地球物理勘探 , 2007, 42(2): 180–185. Wu J F, Yao Y, Sa L M. Analysis on seismic response of special cavernous structure of carbonate. Oil Geophysical Prospecting (in Chinese) , 2007, 42(2): 180-185. |
| [10] | 彭真明, 李亚林, 巫盛洪, 等. 碳酸盐岩储层多角度弹性阻抗流体识别方法. 地球物理学报 , 2008, 51(3): 881–885. Peng Z M, Li Y L, Wu S H, et al. Discriminating gas and water using multi-angle extended elastic impedance inversion in carbonate reservoirs. Chinese J. Geophys. (in Chinese) , 2008, 51(3): 881-885. |
| [11] | 何晓松, 孙林, 张红斌, 等. 盐下碳酸盐岩储层礁体识别. 石油地球物理勘探 , 2009, 44(1): 98–100. He X S, Sun L, Zhang H B, et al. Sub-salt carbonate reef reservoir identification. Oil Geophysical Prospecting (in Chinese) , 2009, 44(1): 98-100. |
| [12] | Kozlov E, Barasky N, Korolev E, et al. Imaging scattering objects masked by specular reflections. 74th SEG meeting, Denver, Colorado, USA, Expanded Abstracts, 2004. 1131-1135. |
| [13] | Moser T J, Howard B C. Diffraction imaging in depth. Geophysical Prospecting , 2008, 56(5): 627-641. DOI:10.1111/gpr.2008.56.issue-5 |
| [14] | Bansal R, Imhof M G. Diffraction enhancement in prestack seismic data. Geophysics , 2005, 70(3): V73-V79. DOI:10.1190/1.1926577 |
| [15] | Khaidukov V, Landa E, Moser T J. Diffraction imaging by focusing-defocusing:An outlook on seismic superresolution. Geophysics , 2004, 69(6): 1478-1490. DOI:10.1190/1.1836821 |
| [16] | Nowak E J, Imhof M G. Diffractor localization via weighted Radon transforms. 74th SEG meeting, Denver, Colorado, USA, Expanded Abstracts, 2004. 2108-2111. |
| [17] | Fomel S. Applications of plane-wave destruction filters. Geophysics , 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [18] | Taner M T, Fomel S, Landa E. Separation and imaging of seismic diffractions using plane-wave decomposition. 76th SEG meeting, New Orleans, Louisiana, USA, Expanded Abstracts, 2006. 2401-2405. |
| [19] | Fomel S, Landa E, Taner M T. Poststack velocity analysis by separation and imaging of seismic diffractions. Geophysics , 2007, 72(6): U89-U94. DOI:10.1190/1.2781533 |
| [20] | Zhu X S, Wu R S. Imaging diffraction points using the local image matrices generated in prestack migration. Geophysics , 2010, 75(1): S1-S9. |
| [21] | 朱生旺, 曲寿利, 魏修成, 等. 通过压制共散射点道集映射噪声改善绕射波成像分辨率. 石油物探 , 2010, 49(2): 107–114. Zhu S W, Qu S L, Wei X C, et al. To improve imaging resolution by mapping noise attenuation on CPS gathers. Geophysical Prospecting for Petroleum (in Chinese) , 2010, 49(2): 107-114. |
| [22] | Cohen J K, Bleistein N. An inverse method for determining small variations in propagation speed. SIAM Journal on Applied Mathematics , 1977, 32(4): 784-799. DOI:10.1137/0132066 |
| [23] | Tarantola A. Inversion of seismic reflection data in the acoustic approximation. Geophysics , 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [24] | Mora P. Nonlinear two-dimensional elastic inversion of multioffset seismic data. Geophysics , 1987, 52(9): 1211-1228. DOI:10.1190/1.1442384 |
| [25] | Mora P. Inversion=migration+tomography. Geophysics , 1989, 54(12): 1575-1586. DOI:10.1190/1.1442625 |
| [26] | Pratt R G. Frequency-domain elastic wave modeling by finite differences:A tool for crosshole seismic imaging. Geophysics , 1990, 55(5): 626-632. DOI:10.1190/1.1442874 |
| [27] | Pratt R G. Seismic waveform inversion in the frequency domain, Part 1:Theory and verification in a physical scale model. Geophysics , 1999, 64(3): 888-901. DOI:10.1190/1.1444597 |
| [28] | Pratt R G, Shipp R M. Seismic waveform inversion in the frequency domain, Part 2:Fault delineation in sediments using crosshole data. Geophysics , 1999, 64(3): 902-914. DOI:10.1190/1.1444598 |
| [29] | 杜正聪, 贺振华, 黄德济. 缝洞储层地震波场数值模拟. 勘探地球物理进展 , 2003, 26(2): 103–108. Du Z C, He Z H, Huang D J. Seismic wavefield numerical simulation of fractured reservoir. Progress in Exploration Geophysics (in Chinese) , 2003, 26(2): 103-108. |
| [30] | 卢明辉, 张才, 徐基祥, 等. 溶洞模型逆散射成像技术. 石油勘探与开发 , 2010, 37(3): 330–338. Lu M H, Zhang C, Xu J X, et al. Inverse-scattering imaging of cavern models. Petroleum Exploration and Development (in Chinese) , 2010, 37(3): 330-338. |
| [31] | LeBras R, Clayton R W. An iterative inversion of back-scattered acoustic waves. Geophysics , 1988, 53(4): 501-508. DOI:10.1190/1.1442481 |
| [32] | Lambaré G, Virieux J, Mandariaga R, et al. Iterative asymptotic inversion in the acoustic approximation. Geophysics , 1992, 57(9): 1138-1154. DOI:10.1190/1.1443328 |
| [33] | Nemeth T, Wu C, Schuster G T. Least-squares migration of incomplete reflection data. Geophysics , 1999, 64(1): 208-221. DOI:10.1190/1.1444517 |
| [34] | Kuehl H, Sacchi M D. Split-step WKBJ least-squares migration/inversion of incomplete data. 5th SEGJ international Symposium-Imaging. Technology, 2001. |
| [35] | 贾晓峰, 胡天跃. 滑动最小二乘法求解地震波波动方程. 地球物理学进展 , 2005, 20(4): 920–924. Jia X F, Hu T Y. Solving seismic wave equation by moving least squares(MLS)method. Progress in Geophysics (in Chinese) , 2005, 20(4): 920-924. |
| [36] | 邹强, 周熙襄, 钟本善. 旅行时与波阻抗联合反演求取层速度. 石油地球物理勘探 , 2003, 38(4): 396–399. Zou Q, Zhou X X, Zhong B S. Acquiring interval velocity by joint inversion of travel-time and wave impedance. Oil Geophysical Prospecting (in Chinese) , 2003, 38(4): 396-399. |
| [37] | 高建军, 陈小宏, 李景叶, 等. 不规则地震数据的抗假频重建方法. 石油地球物理勘探 , 2010, 45(3): 326–331. Gao J J, Chen X H, Li J Y, et al. Studies on anti-aliasing reconstruction method for irregular seismic data. Oil Geophysical Prospecting (in Chinese) , 2010, 45(3): 326-331. |
| [38] | 马继涛, 陈小宏, 黄小宁. 反数据域压制多次波方法研究. 石油地球物理勘探 , 2009, 44(5): 537–542. Ma J T, Chen X H, Huang X N. Studying on multiple elimination in inverse data domain. Oil Geophysical Prospecting (in Chinese) , 2009, 44(5): 537-542. |
| [39] | 杨其强, 张叔伦. 最小二乘傅立叶有限差分偏移. 地球物理学进展 , 2008, 23(2): 433–437. Yang Q Q, Zhang S L. Least-squares Fourier finite-difference migration. Progress in Geophysics (in Chinese) , 2008, 23(2): 433-437. |
| [40] | 黄建平, 李振春, 刘玉金, 等. 复杂介质最小二乘叠前深度偏移方法研究. 地球物理学进展 , 2013(In press). Huang J P, Li Z C, Liu Y J, et al. The study of the least square pre-stack depth migration on complex media. Progress in Geophysics (in Chinese) , 2013(In press). |
| [41] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [42] | 刘红伟, 刘洪, 邹振. 地震叠前逆时偏移中的去噪与存储. 地球物理学报 , 2010, 53(9): 2171–2180. Liu H W, Liu H, Zou Z. The problems of denoise and storage in seismic reverse time migration. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2171-2180. |
| [43] | 刘红伟, 刘洪, 李博, 等. 起伏地表叠前逆时偏移理论及GPU加速技术. 地球物理学报 , 2011, 54(7): 1883–1892. Liu H W, Liu H, Li B, et al. Pre-stack reverse time migration for rugged topography and GPU acceleration technology. Chinese J. Geophys. (in Chinese) , 2011, 54(7): 1883-1892. |
 2013, Vol. 56
2013, Vol. 56

