2. 高速铁路线路工程教育部重点实验室, 成都 610031
2. MOE Key Laboratory of High-speed Railway Engineering, Chengdu 610031, China
自英国学者Rayleigh[1]发现瑞利面波的存在并揭示瑞利面波在弹性半空间介质中的传播特性以来,由于瑞利(Rayleigh)面波采集简便、面波速度VR与横波速度VS相近、且具有速度频散[2-3]等运动学特性,而被广泛研究并应用于地壳结构、石油及工程等各种地下调查领域.如在工程应用中,StokeⅡ和Nazarian等[4],提出了面波频谱分析方法SASW,通过分析瑞利面波速度频散曲线建立近地表S波速剖面.美国Kansas大学地质调查所的Xia等[2]提出了瑞利面波的多道分析方法MASW,反演估算近地表横波波速.2003年,Xia等[5]又首次提出利用瑞利面波的基阶和高阶模式进行联合反演的方法.目前,瑞利面波方法已成为近地表和大型土木工程基础探测的重要方法.
瑞利面波理论和方法的研究主要集中在面波激励场源和观测参数方面.根据场源的激励方式,瑞利面波可分为主动源面波法和被动源面波法[6];按观测参数的不同,可分为面波速度频散特征的观测和质点位移特征的观测两类,或者说是对面波运动学特征和动力学特征参数观测的两类.
传统的瑞利面波的研究和应用主要集中在对主动源瑞利面波的运动学特征--速度频散特征的研究和应用方面.速度频散曲线的提取方法主要是利用频率-波数(F-K)变换或慢度-频率(P-F)变换[7].近年来,研究学者利用空间相关技术(SPAC)[8-9]从地脉动信息中提取面波的速度频散特征.但无论是主动源还是被动源面波法,提取速度频散曲线都需要在观测时布置多个具有一定道间距的检波器的观测排列,且勘探深度与排列长度成正比.因此,以观测速度频散等运动学特征为主的瑞利面波法,在实际应用中容易受场地限制,不适合人口稠密、空间狭小的城市及交通繁忙的公路等场区.
1989年,Nakamura[10]首次提出地脉动信息的单点谱比法-H/V谱比或HVSR法.野外实际观测表明单个三分量检波器采集的地脉动信息的水平分量和垂直分量的频谱比与场地VS结构之间具有较好的对应关系.Arai和Tokimatsu[11]及张立等[12]给出了利用地脉动的HVSR数据反演场地VS剖面的实例.2011年Haney等[13]对实际观测到的被动源面波的椭圆极化进行了分析研究.HVSR法的工程应用展示了基于单点地脉动信息的动力学特征评价场地VS结构的实际可行性.但地脉动信息所包含波的主要成分具有争议性[11-23],如有研究学者认为其主要成分是基阶瑞利面波[14-18],有的认为是高阶瑞利面波[11, 21-22],还有的认为是勒夫面波[19-20],甚至有研究人员认为在某些条件下其主要成分是体波[24-25],此外,再加上地脉动信息场源所具有的随机性和复杂性,从而使得对地脉动随机波场的正演数值模拟和理论研究不完备[26]等因素,导致HVSR法缺乏系统的应用理论基础的支持.
本文基于瑞利面波理论解,对水平层状介质中的基阶瑞利面波的椭圆极化特征进行正演数值模拟,明确了瑞利面波的水平分量和垂直分量的频谱比(HVSR)物理实质上表征的是瑞利面波的椭圆极化的频散特征,该频散特征与场地的泊松比结构密切相关.以期为发展基于单点瑞利面波的动力学特征的HVSR方法奠定理论基础.
2 水平层状介质中Rayleigh面波位移矢量本节在朱介寿等[28]研究成果的基础上,推导了水平层状介质地表上Rayleigh面波水平位移ux和垂直位移uz计算公式,具体计算过程如下.
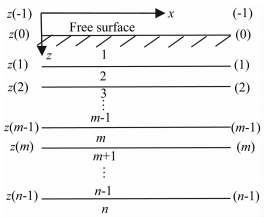
平面地震波在n层水平均匀介质组成的层状空间中传播,层状空间如图 1[28]所示,设x轴沿测线方向,z轴垂直向下,各层及界面编号如图 1所示.
对于第m层,其参数分别为
ρm为密度;dm为厚度;μm,μm为Lame常数;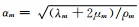
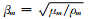
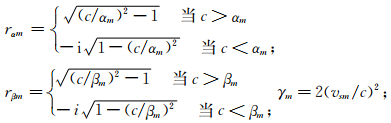
|
ux,uz为质点沿x,z方向的位移;σm,τm为分别法向应力和切向应力;波数k=ω/c=2π/λ,ω为角频率.
由层状介质中平面波传播的波动方程:
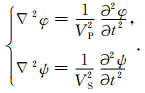
|
(1) |
式中,φ、ψ为纵、横波位移位函数,可表示为
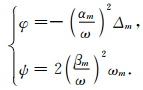
|
(2) |
其中,

|
则层状介质内任一m界面上位移和应力分量为
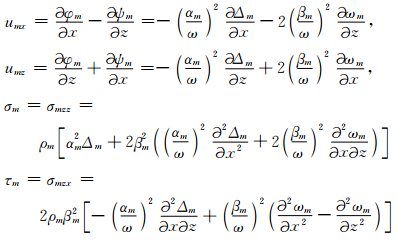
|
(3) |
Δ′m、Δ″m、ω′m、ω″m为常系数.当rαm为实数时,Δ′m表示与z轴正方向夹角沿arctanrαm方向传播的平面波(下行波),即通过层状介质传播的体波;当rαm为虚数时,Δ′m表示沿x轴正方向传播的面波,其振幅随着深度增大而呈指数规律衰减.当rαm为实数时,Δ″m表示与z轴负方向夹角沿arctanrαm方向传播的平面波(上行波),即通过层状介质传播的体波;当rαm为虚数时,亦表示沿x轴方向传播的面波.对于ω′m、ω″m,只要将rαm改为rβm,也可按上述类似方式定义.令:
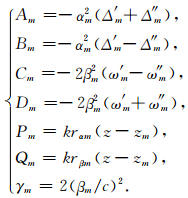
|
(4) |
将(3)式中含有jkrz因子的指数函数改为三角函数,只考虑实数部分.并根据层状介质内任一界面上umx,umz,τm,σm四个量连续条件,可得n层介质位移及应力的4n-2阶的线性方程组:
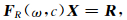
|
(5) |
其中,FR(ω,c)系数矩阵为面波的频散方程.与位移有关的待求变量项:
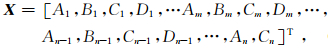
|
(6) |
对于平面波,右端项R=0.方程有解的条件是:
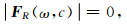
|
(7) |
即方程(5)为齐次方程组.为求解该齐次方程组,将系数矩阵FR(ω,c)、未知数向量X和右端矢量R进行如下处理:设第一层介质中波幅值A1已知,不失一般性,A1=1.将未知矢量X和右端矢量R同除以A1,然后将其代入(5)式中,并将展开后的第一列,即与A1相关项,移到方程右端,经过整理,方程(5)变为非齐次方程组(为方便起见,新方程以F′R(ω,c)、X′、R′表示):
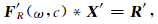
|
(8) |
此时,方程(8)中系数矩阵F′R(ω,c)为4n-3阶方阵.
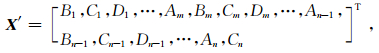
|
(9) |
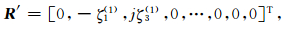
|
(10) |
其中,ζ1(m)=cosPm,ζ3(m)=rαmsinPm.
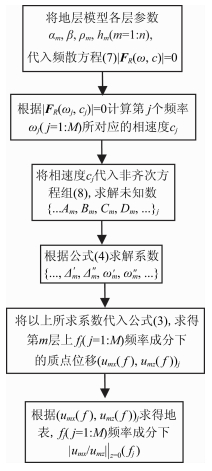
综上,图 2给出了求解任一界面m上位移umx,umz的流程图.首先将层状介质模型各层纵横波速、密度及层厚:αm,βm,ρm,hm(m=1:n)等参数代入频散方程(7)中,然后根据方程|FR(ωj,cj)|=0(j 1:m)计算第j个频率ωj所对应的基阶面波的相速度cj.再将相速度cj代入式(8)中便可求解X,得到Am,Bm,Cm,Dm等量.然后根据式(4)求得系数Δ′m,Δ″m,ω′m,ω″m,将Δ′m,Δ″m,ω′m,ω″m代入质点位移式(3),便可求得频率为fj时,第m层中时基阶面波质点位移的水平分量和垂直分量(umx(fj),umz(fj)).
|
图 2 质点位移及椭圆极化特性正演数值模拟研究程序流程框图 Fig. 2 The numerical simulation flow diagram for the elliptic polarization characters of particle displacement |
根据以上求解,可求得当z=0时,地表处不同频率fj条件下,基阶面波质点位移的水平分量和垂直分量umx|z=0(fj)=ux(fj)、umz|z=0(fj)=uz(fj).在弹性介质条件下,umx(f)、umz(f)分别代表基阶面波质点椭圆运动轨迹的水平轴和垂直轴,因此,借鉴地脉动HVSR方法(1989,Nakamura)中水平分量和垂直分量频谱之比的表示方法,本文基于|ux(fj)/uz(fj)|,或简写为|ux/uz|(fj)的分析,研究基阶瑞利面波质点运动的椭圆极化特征.
显然,当|ux/uz|(fj)>1时,水平轴为长轴,垂直轴为短轴,椭圆呈水平极化现象.当|ux/uz|(fj)<1时,水平轴为短轴,垂直轴为长轴,椭圆呈垂直极化现象.由此,根据文献[28]对瑞利面波速度频散的定义,本文将瑞利面波椭圆极化特性即|uz/xz|(f)随f变化而变化的现象,定义为瑞利面波的椭圆极化频散现象,并称|ux/uz|(f)为瑞利面波椭圆极化频散曲线.为研究方便,在分析中,将椭圆极化频散曲线取10为底的对数.
基于以上推导的理论公式和分析,本文对以下常见的三种工程地震勘探地层模型[29-32]:(1)均匀半无限空间地层模型,(2)正向结构地层模型(VS随着埋深增大而增大)和(3)含有软弱夹层结构的地层模型的椭圆极化频散特性进行数值模拟研究.
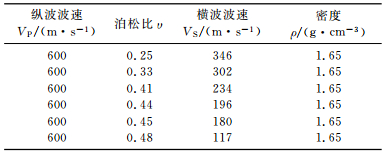
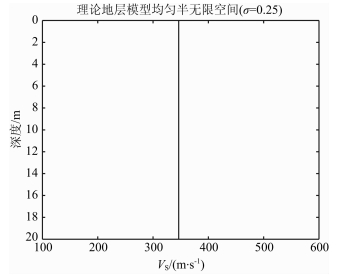
3.1 均匀半无限空间地层模型该组地层模型的泊松比结构特征如表 1所示.由于一般介质的泊松比在0~0.5之间变化,如流体的泊松比0.5,软沉积物的泊松比0.45,大多数岩石的泊松比为0.25,极坚硬的刚性岩石泊松比为0.05,即介质的弹性及强度越大,泊松比越小.因此,设计模型泊松比ν在[0.25,0.48]之间变化,横波波速VS随着泊松比的变化而变化,纵波波速VP,密度ρ等其它参数为常数.图 3所示为该组模型中VP=600m·s-1,ν=0.25,VS=346m·s-1的均匀半无限空间模型.
|
|
表 1 均匀半无限空间地层模型参数 Table 1 The model parameters for the half infinite homogeneous space |
|
图 3 均匀半无限空间地层模型VP=600m·s-1,VS=346m·s-1,ν=0.25 Fig. 3 The half infinite homogeneous space stratum model |
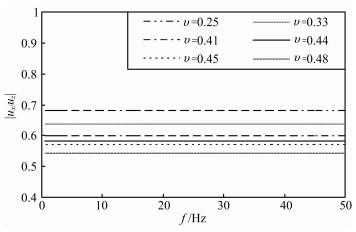
对该组模型的椭圆极化频散特征数值模拟结果见图 4.图中表明,在泊松比一定的均匀半无限空间地层模型中,瑞利面波的椭圆极化频散曲线是水平直线,即泊松比一定时,椭圆极化频散特|ux/uz||z=0(f)是一与f无关的常数,并且对于泊松比不同的均匀半无限空间地层模型,|ux/uz||z=0(f)值不同,表明在均匀介质中,瑞利面波不存在椭圆极化频散现象.此外,对于泊松比不同的均匀半无限空间地层模型,随着泊松比的增大,椭圆极化频散|ux/uz||z=0(f)的值逐渐减小,即随着泊松比的增大,介质越松软,椭圆越趋于垂直极化现象.这不难用泊松比是介质横向应变与纵向应变之比的物理定义来解释.因此,|ux/uz||z=0(f),或其的倒数实质上反映的是介质泊松比度量,具有定性评价介质弹性性质和强度等物理力学性质的应用前景.
|
图 4
泊松比不同的均匀半无限空间地层模型自由表面上椭圆极化频散曲线(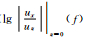 |
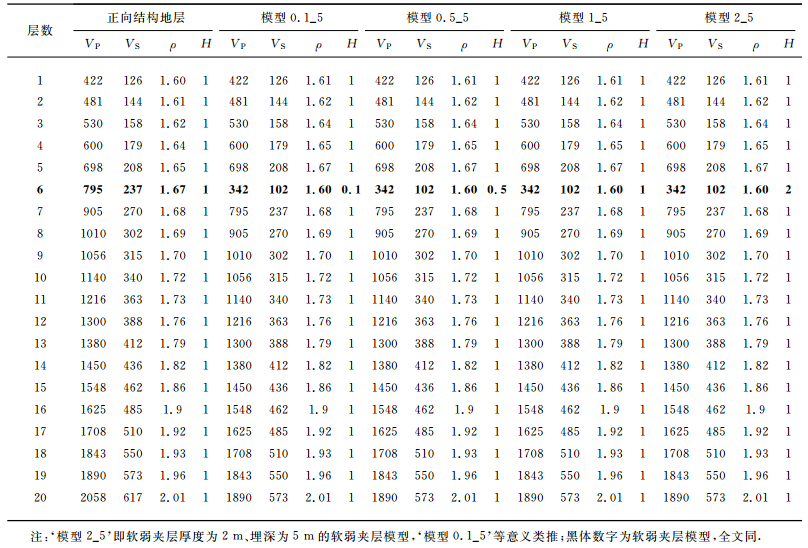
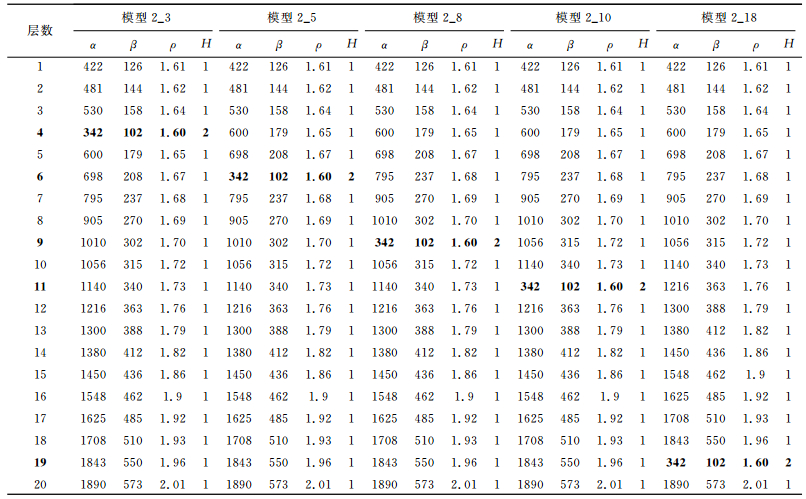
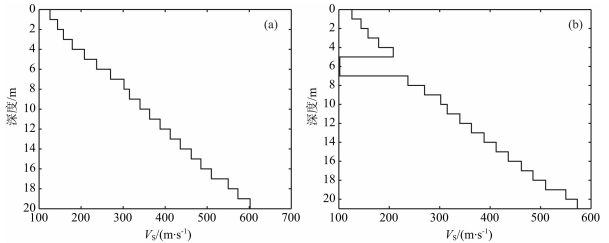
该组地层模型以单层厚度1m、各层VS随深度递增的20层正向结构地层模型为背景,均含有埋深为5m、夹层厚度在0.1~2 m之间变化的软弱夹层.所有模型中,第一层参数均为VS=126m·s-1,VP=422m·s-1,ρ=1.61g·cm-3,h=1 m;软弱夹层的VS=102 m·s-1,VP=342 m·s-1,ρ=1.6g·cm-3,h=0.1~2m.随着深度的增大,各层VP与VS近似符合一定的线性变化规律[29-33],密度ρ1~ρ20在1.6~2.01g·cm-3之间呈线性变化[29-33](表 2).图 5(a、b)分别显示了‘正向结构地层模型’和‘模型2_5’.模型椭圆极化频散曲线|ux/uz||z=0(f)和速度频散曲线的数值模拟结果见图 6所示.
|
|
表 2 软弱夹层厚度不同、埋深相同的地层模型参数 Table 2 The parameters of the models with a interbeded soft layer into abackground model of elastic parameter increasing with depth increasing. |
|
图 5 正向结构地层模型和软弱夹层地层模型2_5(软弱夹层厚2m、埋深5m) (a)正向结构地层模型VP1=422m·s-1,VS1=126m·s-1;(b)软弱夹层地层模型2_5. Fig. 5 The model with a interbeded soft layer into a background of elastic parameter increasing with depth increasing. (a) The background model of elastic parameter increasing with depth increasing with VP1=422 m·s-1, VS1=126 m·s-1; (b)Model 2_5 with a interbeded soft layer. |
|
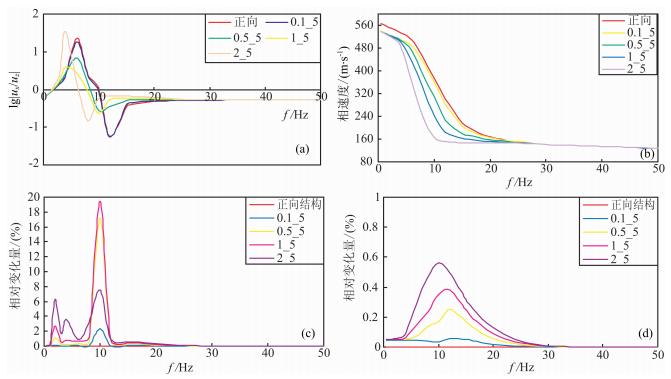
图 6 软弱夹层厚度不同、埋深相同的地层模型椭圆极化频散曲线和速度频散曲线理论计算图 (a)椭圆极化频散曲线图;(b)速度频散曲线图;(c)相对正向结构地层模型|ux/uz||z(f)变化量;(d)相对正向结构地层模型速度频散曲线变化量. Fig. 6 The elliptic polarization dispersion curves and velocity dispersion curves for the stratum models with the background increasing S-wave velocity with increasing buried depth intercalated a soft layer with various thickness and same burial depth. (a) The elliptic polarization dispersion curves; (b) The velocity dispersion curves; (c) The variation of the elliptic polarization dispersion curves compared with forward stratum models; (d) The variation of the velocity dispersion curves co m pared with forward direction stratum models. |
从图 6a可看出,该模型中瑞利面波椭圆极化频散曲线不再是直线,而是随着f的变化而变化.这表明,对于非均匀介质,瑞利面波存在椭圆极化频散特性.并且随着模型软弱夹层厚度在一定范围内变化,与模型相应的椭圆极化频散曲线也随之变化,模型的椭圆极化频散曲线在具有明显的正负单峰值.如图 6a中正向结构地层模型的|ux/uz||z=0(f)曲线在f0=6Hz附近达到正峰值,在f0=12Hz附近有负峰值,模型2_5的曲线在f0=4 Hz附近出现正峰,在主f0=8Hz附近出现负峰.正、负单峰值对应的频率随着模型软弱夹层厚度的增大均向低频端移动.此外,椭圆极化频散曲线|ux/uz||z=0(f)异常幅值随着软弱夹层的厚度H变化,具有最大软弱夹层厚度模型2_5的|ux/uz||z=0(f)曲线与正向结构地层模型曲线的差异最明显,而随着H→0,椭圆极化频散曲线|ux/uz||z=0(f)也趋近于正向结构地层模型的曲线.
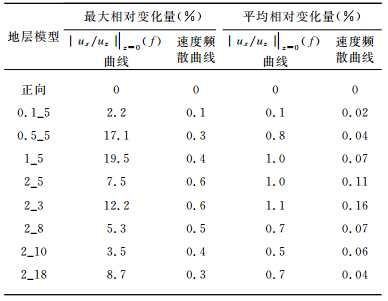
图 6b为该模型速度频散曲线数值模拟结果.为对比,图 6(c、d)和表 3分别是相对于正向结构地层模型的|ux/uz||z=0(f)曲线和速度频散曲线的相对变化图和变化量表.在该地层模型中,|ux/uz||z=0(f)曲线的相对变化量较大,最大值在2%~20%之间,平均变化量在0.1%~1.1%之间;相应的速度频散曲线的相对变化较小,最大值在0~0.6%之间,平均变化量在0~0.1%之间.如模型1_5,它的|ux/uz||(f)曲线的相对变化量最大近20%,平均变化量1.04%,而速度频散曲线的相对变化量最大为0.38%,平均变化量为0.07%.这表明椭圆极化频散曲线对模型参数变化的灵敏度比速度频散曲线更高.
|
|
表 3 含软弱夹层的理论模型相对正向结构模型的|ux/uz||z=0(f)曲线和速度频散曲线的相对变化量 Table 3 The variation of the elliptic polarization dispersion and the velocity dispersion compared with the forward stratum models |
该地层模型同样以图 6a中的正向结构地层模型为背景,且所有模型各层的参数VP、VS及ρ的大小及变化规律均与第二组模型相同,且模型的名称及意义同,但模型中软弱夹层固定厚度为2m、埋深在3~30m之间变化,模型具体参数见表 4.
|
|
表 4 软弱夹层厚度相同、埋深不同的地层模型参数 Table 4 The parameters of the interbeded soft layer models with fixed thickness and various burial depth |
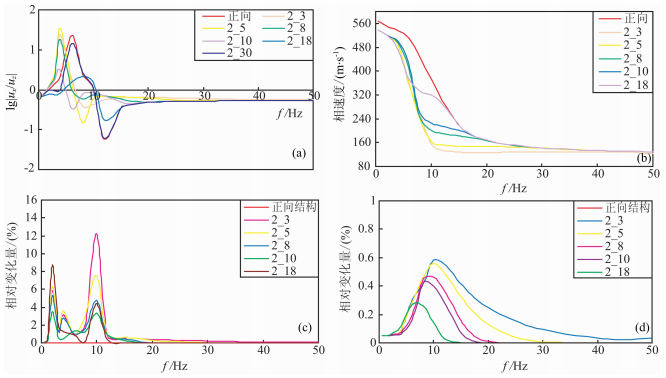
图 7显示了该组地层模型椭圆极化频散|ux/uz||z=0(f)和速度频散数值模拟结果.从图 7a可看出,该模型中瑞利面波椭圆极化频散曲线也随着f的变化而变化,即|ux/uz||z=0(f)也与f有关,该结果同样证明对于非均匀介质,瑞利面波存在椭圆极化频散特性,且椭圆极化频散现象与软弱夹层的埋深有关.
|
图 7 软弱夹层厚度相同、埋深不同的地层模型椭圆极化频散曲线和速度频散曲线模拟计算图 (a)椭圆极化频散曲线图;(b)速度频散曲线图;(c)相对正向结构地层模型|ux/uz||z=0(f)变化量;(d)相对正向结构地层模型速度频散曲线变化量. Fig. 7 The elliptic polarization dispersion curves and velocity dispersion curves for the stratum models with the background increasing S-wave velocity with increasing buried depth intercalated a soft layer with various burial depth and same thickness (a) The elliptic polarization dispersion curves; (b) The velocity dispersion curves; (c) The variation of the elliptic polarization dispersion curves compared with for ward stratum models; (d) The variation of the velocity dispersion curves compared with for ward direction stra |
从图 7a还可发现,该组模型的椭圆极化频散曲线同样以正、负单峰值为异常特征.随着软弱夹层埋深的逐渐增大,异常的正、负单峰值先向低频端而后向高频端移动,|ux/uz||z=0(f)曲线也随之先偏离而后趋近于正向结构地层模型的椭圆极化频散曲线.
此外,椭圆极化频散曲线|ux/uz||z=0(f)异常幅值随着软弱夹层的埋深变化,具有最小(→0)或最大(→∞)软弱夹层埋深的模型如2_3和2_18的椭圆极化频散曲线趋近于正向结构地层模型曲线,而随着埋深在一定范围时如模型2_10,椭圆极化频散曲线与正向结构地层模型曲线的差异最明显.
图 7b为该地层模型的速度频散曲线数值计算结果.图 7(c,d)和表 3分别为该组模型相对于正向结构地层模型椭圆极化频散曲线和速度频散曲线的相对变化图和变化量表.图 7及表 3数据显示,在该组地层模型中椭圆极化频散曲线的相对变化较大,最大值在3%~13%之间,平均值在0.4%~1.2%之间;相应的速度频散曲线的相对变化较小,其最大值范围在0~0.6%之间,平均变化在0~0.2%之间.如模型2_3的椭圆极化频散曲线相对变化量的最大值接近13%,平均变化量为1.14%,而该模型的速度频散曲线相对变化量最大不到0.6%,平均变化量仅为0.16%.
上述研究表明,相对于正向结构地层模型而言,随着软弱夹层埋深在一定范围内的变化,相应模型的椭圆极化频散曲线也随之变化,即曲线与模型之间为一一对应关系,且椭圆极化频散曲线对模型变化的反应比速度频散曲线更敏感.
4 结论本文以工程中常见的几种典型地层模型(均匀半无限空间地层模型、正向结构地层模型和含有软弱夹层的地层模型)为例,应用HVSR方法,对基阶瑞利面波的正演理论基础--面波质点位移水平分量与垂直分量之比随频率f的变化规律|ux/uz||z=0(f),即基阶瑞利面波的椭圆极化频散特征进行了数值模拟研究,得到如下结论:
(1)均匀介质中基阶瑞利面波不存在椭圆极化频散现象,而在非均匀介质中基阶瑞利面波存在椭圆极化频散现象.
(2)以|ux/uz||z=0(f)表征的椭圆极化频散特性,或其倒数实质上是介质泊松比度量,具有定性评价介质弹性性质和强度等物理力学性质的应用前景.
(3)在本文研究模型范围内,基阶瑞利面波椭圆极化频散曲线对地层VS结构反应的灵敏度比速度频散曲线更高.
(4)瑞利面波动的椭圆极化频散曲线计算仅需面波单点的多分量数据特性,展示了单点面波调查方法的潜在发展前景.
此外,需要说明的是:
(1)本文所有计算研究过程中不考虑介质的耗散作用,则质点运动不考虑出现椭圆斜极化[28]现象.
(2)本文所选模型是以工程勘探中常遇到的软地层条件为背景,其波速较低,对于硬地层模型还需要做进一步研究.
| [1] | Rayleigh L. On waves propagated along the plane surface of an elastic solid. Proc. Lond. Math. Soc. , 1885, 17(1): 4-11. |
| [2] | Xia J H, Miller R D, Park C B. Estimation of near surface shear wave velocity by inversion of Rayleigh waves. Geophysics , 1999, 64(3): 691-700. DOI:10.1190/1.1444578 |
| [3] | Dorman J, Ewing M. Numerical inversion of seismic surface wave dispersion data and crust-mantle structure in the New York-Pennsylvania area. Journal of Geophysical Research , 1962, 67(13): 5227-5241. DOI:10.1029/JZ067i013p05227 |
| [4] | Stoke Ⅱ K H, Nazarian S. Effectiveness of ground improvement from spectral analysis of surface waves//Proc. 8th. Euro Conf on Soil Mech and Found Engrg. Cambridge:Cambridge University Press, 1983. http://www.oalib.com/references/18986822 |
| [5] | Xia J H, Miller R D, Park C B, et al. Inversion of high frequency surface waves with fundamental and higher modes. Journal of Applied Geophysics , 2003, 52(1): 45-57. DOI:10.1016/S0926-9851(02)00239-2 |
| [6] | Geophysical Service. Active and Passive Surface wave Techniques, www.geovision.com. |
| [7] | Capon J. High-resolution frequency wave number spectrum analysis. Proc. IEEE , 1969, 57(8): 1408-1418. DOI:10.1109/PROC.1969.7278 |
| [8] | Aki K. Space and time spectra of statinary stochastic waves with special reference to microtreors. Bull. Earthq. Res. Inst. , 1957, 35: 415-456. |
| [9] | Hortencia Flores Estrella. Jorge Aguirre Gonzalez, SPAC:An alternative method to estimation earthquake site effects in mexico city. Geofisica Internacional , 2003, 42(2): 227-236. |
| [10] | Nakamura Y. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Quart. Rept. RTRI Japan , 1989, 30: 25-33. |
| [11] | Arai H, Tokimatsu K. S-wave velocity profiling by inversion of microtremor H/V Spectrum. Bull. Seism. Soc. Am , 2004, 94(1): 53-63. DOI:10.1785/0120030028 |
| [12] | 张立, 刘争平, 熊自英. 利用地脉动H/V谱比反演地层Vs结构剖面. 工程地球物理学报 , 2009, 6(SI): 4–5. Zhang L, Liu Z P, Xiong Z Y. S-wave velocity profiling by inversion of microtremor H/V spectra. Chinese Journal of Engineering Geophysics (in Chinese) , 2009, 6(SI): 4-5. |
| [13] | Haney M M, Nies A, Masterlark T, et al. Interpretation of Rayleigh-wave ellipticity observed with multicomponent passive seismic interferometry at Hekla Volcano, Iceland. The Leading Edge , 2011, 30(5): 526-531. DOI:10.1190/1.3589111 |
| [14] | Lachet C, Bard P Y. Numerical and theoretical investigations on the possibilities and limitations of nakamura's technique. J. Phys. Earth , 1994, 42(5): 377-397. DOI:10.4294/jpe1952.42.377 |
| [15] | Nogoshi M, Igarashi T. On the Amplitude Characteristics of Microtremor-part2(in Japanese with English abstract). J. Seism. Soc. Japan , 1971, 24: 26-40. |
| [16] | Konno K, Ohmachi T. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor. Bull. Soc. Am. , 1998, 88(1): 228-241. |
| [17] | Tokimatsu K, Shinzawa K, Kuwayama S. Use of short-period microtremors for Vs profiling. J. Geotech. Rngrg. ASCE , 1992, 118(10): 1544-1588. DOI:10.1061/(ASCE)0733-9410(1992)118:10(1544) |
| [18] | Horike M. Inversion of phase velocity of long-period microtremors to the S-wave-velocity structure down to the basement in urbanized area. J. Phys. Earth. , 1985, 33(2): 59-96. DOI:10.4294/jpe1952.33.59 |
| [19] | Matsushima T, Okada H. An exploration methof using microtremors (2)-An pxperiment to identify Love waves in long-period microtremors-. Proc. The 82nd SEGF Conf , 1990: 5-8. |
| [20] | Tokimatsu K, Arai H, Asaka Y. Deep shera-wave structure and earthquake ground motion characteristics in Sumiyoshi area, Kobe city, based on microtremor measurements. J. Struct. Constr. Engng AIJ , 1997, 491: 37-45. |
| [21] | Yutaka Nakamura. On the H/V spectrum. The 14th World Conference on Earthquake Engineering. 2008, Beijing, China. |
| [22] | Tokimatsu K, Miyadera Y. Characteristics of Rayleigh waves in microtremors and their relation to underground structures. J. Struct, Constr, Engng, AIJ , 1992, 439: 81-87. |
| [23] | Arai H, Tokimatsu K. Effects of Rayleigh and Love Waves on microtremors H/V spectra. Proc. 12th World Conf. on Earthquake Engineering, 2000, paper 2232, CD-ROM. http://www.oalib.com/references/18986837 |
| [24] | 郭明珠, 谢礼立, 凌贤长. 弹性介质面波地脉动单点谱比法研究. 岩土工程学报 , 2004, 26(4): 450–453. Guo M Z, Xie L L, Ling X Z. Research on spectral ratio of horizontal to vertical component for elastic model and surface microtremors. Chinese Journal of Geotechnical Engineering (in Chinese) , 2004, 26(4): 450-453. |
| [25] | 郭明珠, 谢礼立, 闫维明, 等. 体波地脉动单点谱比法研究. 岩土力学 , 2003, 24(1): 109–112. Guo M Z, Xie L L, Yan W M, et al. Spectral ratio of horizontal to vertical component research for body wave microtremors. Rock and Soil Mechanics (in Chinese) , 2003, 24(1): 109-112. |
| [26] | 刘争平, 张立, 闫胜. 局部非均质体的瑞利面波动力学响应数值模拟研究. 工程地球物理学报 , 2009, 6(S1): 1–3. Liu Z P, Zhang L, Yan S. The dynamic feature analysis of Rayleigh surface wave on a local inhomogeneity using the numerical method. Chinese Journal of Engineering Geophysics (in Chinese) , 2009, 6(S1): 1-3. |
| [27] | Thomson W T. Transmission of elastic waves through a stratified solid medium. Journal of Applied Physics , 1950, 21(2): 89-93. DOI:10.1063/1.1699629 |
| [28] | 朱介寿. 地震学中的计算方法. 北京: 地震出版社, 1988 . Zhu J S. Calculation Method in Seismology (in Chinese). Beijing: Seismological Press, 1988 . |
| [29] | 陶莅宁, 侯广春. 波速测试技术在工程地质勘察中的应用. 山东煤炭科技 , 2008(2): 20–21. Tao L N, Hou G C. Application of wave-speed measure technology in engineering geology survey. Shandong Coal Science and Technology (in Chinese) , 2008(2): 20-21. |
| [30] | 任健. 多道瞬态面波法检测技术在工程勘察中的应用. 陕西水利水电技术 , 1999(1): 45–51. Ren J. Application of multi-channel transient surface wave method in engineering survey detection. Shaanxi Water Conservancy and Hydropower Technology (in Chinese) , 1999(1): 45-51. |
| [31] | 赵明杰, 张桂玉, 刘宾. 瑞利面波在地质勘察中的应用. 华北地震科学 , 2005, 23(3): 31–33. Zhao M J, Zhang G Y, Liu B. Application of Rayleigh wave in geological exploration. North China Earthquake Sciences (in Chinese) , 2005, 23(3): 31-33. |
| [32] | 杜正涛, 刘丽敏, 程道伟. 瑞雷面波勘探技术在第四系分层方面的应用. 物探与化探 , 1999, 23(4): 277–282. Du Z T, Liu L M, Cheng D W. The application of Rayleigh surface wave Exploration Technique to the quaternary stratification. Geophysical & Geochemical Exploration (in Chinese) , 1999, 23(4): 277-282. |
| [33] | 陈仲候, 王兴泰, 杜世汉. 工程与环境物探教程. 北京: 地质出版社, 1999 . Chen Z H, Wang X T, Du S H. Engineering and Environment Geophysical Course (in Chinese). Beijing: Geological Publishing House, 1999 . |
 2013, Vol. 56
2013, Vol. 56