2. 海洋石油勘探国家工程实验室, 西安 710049;
3. 中煤科工集团西安研究院, 西安 710077
2. National Engineering Laboratory for Offshore Oil Exploration, Xi'an 710049, China;
3. Xi'an Research Institute of China Coal Technology & Engineering Group Corp, Xi'an 710077, China
垂直地震剖面(VSP)是一种井中地震观测方法.因为检波器置于井中且与地层直接耦合,所以既能接收到自下而上传播的上行波,也能接收到自上而下传播的下行波.在VSP资料的处理中,波场分离是关键问题之一.
目前常用来分离VSP资料上行波和下行波的方法主要依据两者的视速度不同,这些方法包括:中值滤波法、SVD变换法、多道速度滤波法、组合滤波器法、递归滤波法、F-K滤波法、Radon变换法等[1-8].如果上行波和下行波在分析窗口内满足波形一致性假设,多道速度滤波法、组合滤波器法、递归滤波法等方法可以获得很好的波场分离效果.F-K滤波法、Radon变换法分离VSP资料的上行波和下行波可能会造成一些假能量[9].中值滤波法能较好地保持上下行波的波形和幅值的变化,具有不引入假同相轴的特点,被广泛用于实际VSP资料的上下行波场分离.最近几年,E.Blias[10]提出解决VSP资料的波场分离问题的wave-by-wave方法,有效削弱了各种波互相影响造成的波场分离误差.当数据波形的不一致性可以用时间方向上波形伸缩模型描述时,该方法分离上下行波场具有很好的效果.杜婧等[11]提出利用局部斜率属性的VSP资料波场分离方法,可以很好地衰减阈值滤波器边界造成的假象.
20世纪80年代末,Freire等[6]提出解决VSP资料的波场分离问题的传统SVD法:对排齐下行波的波场分别做“SVD低通滤波”和“SVD带通滤波”得到下行波场和上行波场.一次SVD得到的一组特征图像之间具有正交性,而排齐下行波后,上行波场和下行波场之间不具有严格的正交性,所以无法通过一次SVD变换把上下行波场表示为不同特征图像的线性组合.因此传统的SVD波场分离方法有重构下行波信号的奇异值个数难以确定的问题:如果重构下行波信号使用的奇异值个数较少,就会导致得到的上行波场中含有较强的下行波干扰;如果重构下行波信号使用的奇异值个数较多,得到的上行波场就会有明显的损伤.
随着属性提取技术的发展,特别是最近几年在国内外受到广泛关注的Q值分析技术的发展[12],波场分离方法的保真性变得日益重要,这对传统波场分离方法提出了更高的要求.为了给后续的处理和解释(例如Q值分析)提供对动力学特征具有良好保真性的上下行波场,本文给出一种基于SVD的两步法实现零偏VSP的波场分离.与传统SVD法通过一次SVD分离上下行波场不同,该方法通过两次SVD变换实现:零偏VSP波场中下行波的能量远强于上行波的能量,因此可以在零偏VSP波场中排齐下行波;对排齐下行波的波场做SVD变换,则对应奇异值最大的几个特征图像可以反映下行波场的主要特征,所以通过“SVD高通滤波”可以得到压制下行波主要能量后的剩余波场;在剩余波场中仍然含有下行波场的残余能量,但是上行波场的能量比下行波场的残余能量强,是剩余波场中能量最强的成分,对剩余波场排齐上行波,再做“SVD低通滤波”可以得到上行波场的估计;对下行波场的估计可以通过从VSP波场中减去上行波场的估计得到.
在算法实现过程中,剩余波场中可能含有较强的下行波干扰,上行波同相轴排齐比较困难.为了解决这一问题,本文根据上行波同相轴排齐时各道数据的水平相关程度最大这一原理,构造了一种极大化多道数据相关性(MC)算法实现上行波同相轴的排齐.
本文按照如下方式组织:第二部分简述SVD变换的定义和性质;第三部分给出基于MC算法的同相轴排齐方法;第四部分介绍基于SVD的两步法实现零偏VSP资料的上下行波场分离;第五部分和第六部分分别展示了本文方法对模型数据和实际资料的处理结果,并与传统SVD方法的处理结果进行了对比;第七部分给出结论.
2 SVD变换简述用N行M列的矩阵X表示M道,每道采样点数为N的多道地震记录(通常M<N),则X的SVD可以表示为:
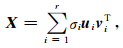
|
(1) |
T表示转置;r是矩阵X的秩,满足r≤M且r≤N;σi是X的奇异值,按降序排列,且满足σi>0;uiviT被称为X的第i个特征图像,显然它的各列具有相同的波形ui;ui是N维单位列向量,vi是M维单位列向量,分别称为X的左奇异向量和右奇异向量,两组向量分别满足两两正交,并且对i0=1,2,…,r有[13]:
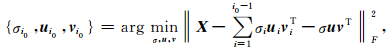
|
(2) |
其中‖·‖F表示F-范数.因此,对于用i0个各列具有相同波形的矩阵线性表示矩阵X的问题,矩阵X的SVD分解的前i0项就是均方误差能量最小意义下的最优解.
设波场X中的某种成分Y在水平方向强相干,即Y在各道的波形非常相似,可以近似认为Y能用i0个各列具有相同波形的矩阵线性表示,其中i0为某个较小的正整数.Y在最小均方误差意义下的估计
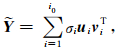
|
(3) |
若Y在X中的能量相对较强,则Ỹ能够反映Y的主要特征,这就是“SVD低通滤波”的原理.i0被称为“SVD低通滤波”的通带宽度,调节i0可以控制滤波效果,i0取值越大,Ỹ中含有Y的细节特征越丰富,同时含有其它成分的干扰和噪声越多.
通过从X中减去Ỹ可以压制波场X中的Y成分,得到剩余波场
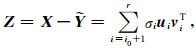
|
(4) |
(4)式被称为“SVD高通滤波”,i0被称为“SVD高通滤波”的阻带宽度,调节i0可以控制滤波效果,i0取值越大,Z中残余Y成分的能量越小,同时其它成分的损伤越大.
若把矩阵X表示成一组列向量(x1,x2,…,xM)的形式,则优化问题
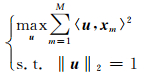
|
(5) |
在u=u1时取得最大值σ12.这说明u1反映了X各道最主要的共同特征,σ12反映了X各道最主要的共同特征的总能量.
3 求解同相轴排齐问题的MC算法波场中能量最强的相干成分同相轴排齐精度越高,波场的水平相关性越强.因此,求解以各道静态时移量为优化变量,极大化反映波场多道之间水平相关性的参数为目标的优化问题,可以解决通过静态时移排齐能量最强相干成分同相轴的问题.
Montagne等[14]在研究地震资料的面波压制问题时指出,波场各列最主要的共同特征的能量除以波场的总能量,其结果可以反映波场的多道水平相关性.对于求解排齐零偏VSP波场中相干成分同相轴的静态时移量问题,由于静态时移不改变波场的能量,极大化反映波场多道水平相关性的参数,等价于极大化波场各列最主要的共同特征的能量.因此可以用波场各列最主要的共同特征的能量作为目标函数构造优化问题,求解排齐波场中能量最强的相干成分同相轴的最佳时移量.
考虑到各道数据附加相同的静态时移量,不影响波场的水平相关性,即各道的静态时移量为(t1,t2,…,tM)或者(t1+τ,t2+τ,…,tM+τ),时移得到的波场水平相关性相同.为了保证使波场的水平相关性最强的静态时移量的唯一性,约束第一道的静态时移量t1=0.
设波场X的第m道数据xm经过静态时移tm得到x′m,tm,u是表示各道数据共同特征的N维向量,记t=(t1,t2,…,tM),X′t={x1,t1,x2,t2,…,xM,tM },最佳时移量t*,求解最佳时移量的问题可以表示为:
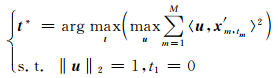
|
(6) |
对于(6)式表述的优化问题,优化变量t和u的维数很高且每一维都互相耦合,直接求解比较困难.交换求极值和求和顺序,可以把(6)式转化为更容易求解的形式:
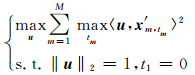
|
(7) |
(7)式可以通过迭代过程求解:时移量t的迭代初值可以通过传统的排齐同相轴方法得到,每步迭代分三个子步骤实现.
(1)固定时移量为t,计算使目标函数达到最大的u,即求解:
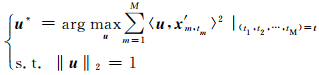
|
(8) |
由第2节(5)式反映的SVD的性质可知,u*为X′t的第一左奇异向量.
(2)固定u,分别对m=1,2,…,M在时移量tm初值附近寻找最佳值tm*,以满足:
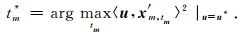
|
(9) |
上面的优化问题在初值附近一般满足上凸性,通过四等分法[15]可以逼近最优解.
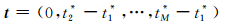
|
(10) |
(7)式可以通过重复上述三个子步骤,不断更新u*和t求解.这样,通过上述迭代过程可以使t逐步逼近最佳时移量t*,实现对于波场中能量最强的相干成分同相轴的排齐.
4 基于SVD的两步法分离零偏VSP资料的上下行波场传统SVD法希望通过排齐下行波同相轴后经过一次SVD变换解决零偏VSP资料上下行波分离问题,这就要求在排齐下行波同相轴后上下行波场具有正交性,事实上零偏VSP资料的上下行波场无法满足这一条件.为了解决这一问题,本文给出了一种通过两次SVD变换实现上下行波场分离的方法,该方法通过两个步骤实现.
设零偏VSP波场X中含有下行波场D,上行波场U,随机噪声N,则有:

|
(11) |
步骤1 计算压制下行波主要能量后的剩余波场R
X中含有下行波场D、上行波场U和随机噪声N.下行波场D是零偏VSP波场X中能量最强的相干成分.首先采用第3节给出的MC方法在原始零偏VSP波场X中排齐下行波的同相轴得到波场X′,排齐同相轴的下行波场D′是X′中在水平方向强相干且能量最强的成分.若对波场X′做SVD变换,由第2节(3)、(4)式可知,压制X′中D′成分得到的剩余波场R′可以通过“SVD高通滤波”得到.对R′反排齐下行波,可以得到压制下行波后的剩余波场R.
计算R′时“SVD高通滤波”阻带宽度的取值,应该以R中的上行波场几乎不受损伤为前提,并且在这个前提下尽可能大,从而在保留上行波场特征的前提下最大程度地压制下行波的能量.
步骤2 计算上行波场的估计Û
R中含有上行波场U、残余下行波场和随机噪声N,上行波场U是其中能量最强的相干成分,可以使用第3节给出的MC方法在R中排齐上行波的同相轴得到R″.排齐同相轴的上行波场U″是R″中在水平方向强相干且能量最强的成分.对R″做SVD变换,根据第2节(3)式可知,U″的估计Û″可以通过“SVD低通滤波”得到.对Û″反排齐上行波,可以得到上行波场U的估计Û.一般零偏VSP波场中的随机噪声能量很小,并且下行波能量远强于随机噪声,因此下行波场的估计
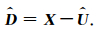
|
(12) |
|
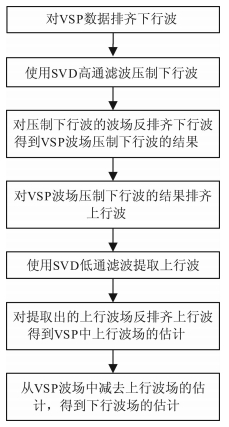
图 1 基于SVD的两步法分离上下行波的流程 Fig. 1 Flow chartof Two-Step SVD |
令检波器间隔为10m,采样周期为1ms,激发源是主频为50 Hz的Ricker子波,根据Ganley [16]提出的方法使用图 2a所示地层模型得到零偏VSP记录(图 2b)和上行波场(图 2c).使用本文方法处理合成零偏VSP记录的过程中,使用MC算法,可以通过两步迭代排齐上行波,效果如图 2d.观察图 2d中椭圆标示处可知,MC算法能够在较低信噪比下有效地排齐上行波.使用本文方法处理合成零偏VSP得到的上行波场如图 2e,下行波场如图 2f.传统SVD法得到的奇异值曲线如图 2h.经过尝试,使用传统SVD法用第3项及以后的全部奇异值合成的上行波场(如图 2g)效果最好.通过对比图 2e和2g与图 2c的差异可知,使用本文方法得到的上行波场的质量与传统SVD法的上行波场相比,更接近合成的上行波场.特别是图 2e和2g中上行波与初至下行波交叉的部分(椭圆标示处),本文方法得到的上行波场中的下行波场的残留能量更小.由本文方法得到的下行波场(图 2f)由VSP波场减去上行波场得到,其中残余上行波非常微弱(例如图 2f椭圆标示处),这表明本文方法得到的上行波场具有良好的保真性.本文方法得到的上行波场(图 2e)中下行波的残余能量也非常微弱(例如图 2e椭圆标示处),由VSP波场减去上行波场对下行波的损伤也非常微弱,这表明本文方法得到的下行波场也具有良好的保真性.从本文方法和传统SVD法得到的下行波场中提取Q值[17],并与模型Q值进行对比,可以得到图 2i.观察图 2i可知,从本文方法得到的下行波场中提取的Q值曲线,可以较好地吻合模型的Q值,而传统SVD法得到的下行波场中提取的Q值曲线的误差很大.这说明本文方法对下行波场动力学特征具有良好的保真性,适合作为Q值提取的预处理步骤.

|
图 2 合成数据算例 (a)地层模型;(b)合成零偏VSP波场;(c)合成上行波场;(d)MC算法排齐上行波的结果;(e)本文方法得到的上行波场. Fig. 2 Synthetic data example (a)The strata model; (b)Synthetic zero-offset VSP data; (c)Synthetic upgoing wavefield; (d)Upgoing wave aligned using MC approach; (e)Upgoing wavefield separated by our method. |
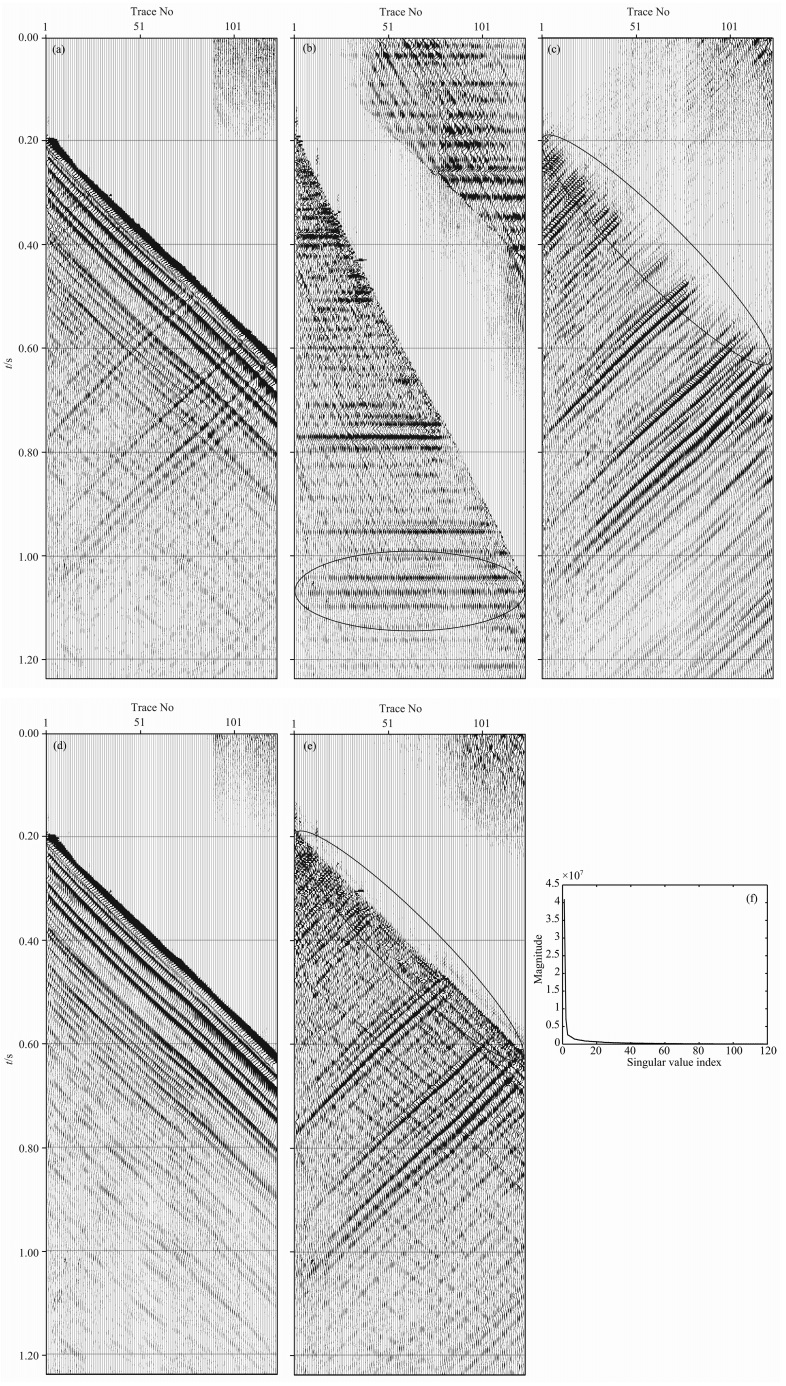
图 3a是某油田一段实测零偏VSP资料,图 3b是使用MC算法经过三步迭代排齐上行波的效果.通过观察图 3b椭圆标示处可知,MC算法在波场中含有下行波干扰的情况下有效地排齐了上行波.图 3c是本文方法得到的上行波场.图 3d是本文方法得到的下行波场.图 3f是传统SVD法的奇异值曲线.图 3e是传统SVD法用第7到第90项奇异值重构得到的上行波场.对比图 3c、3e椭圆标示处可以看出,与传统SVD法相比,本文提出的波场分离方法可以得到下行波干扰和上行波损伤都更少、信噪比更高的上行波场.图 3c中没有明显的下行波,图 3d中没有明显的上行波,VSP资料可以由图 3c和图 3d中的波场之和得到,这验证了本文方法能够较好地分离零偏VSP资料的上下行波场,并具有良好的保真性.
|
图 3 实际VSP资料算例 (a)实际零偏VSP波场;(b)MC算法排齐上行波的结果;(c)本文方法得到的上行波场;(d)本文方法得到的下行波场;(e)传统SVD法得到的上行波场;(f)传统SVD法得到的奇异值曲线. Fig. 3 Real data example Real data example (a)Zero-offset VSP data; (b)Upgoing wave aligned using MC approach; (c)Upgoing wavefield separated by our method; (d)Downgoing wavefield separated by our method; (e)Upgoing wavefield separated by traditional SVD approach; (f)Singular value curve. |
为了给零偏VSP资料的处理和解释(例如Q值分析)提供具有较好保真性的上、下行波场,本文给出了一种通过两次SVD变换实现零偏VSP资料上下行波场分离的方法.该方法先对零偏VSP排齐下行波,再通过“SVD高通滤波”得到压制下行波的主要能量的波场,然后对该波场排齐上行波,最后通过“SVD低通滤波”得到上行波场.在该方法的实现过程中,由于存在较强的残余下行波,排齐上行波的步骤较难实现.本文给出MC算法,通过调整各道数据的静态时移量,使时移后波场的最大奇异值达到极大值,实现了上行波的排齐,在一定程度上解决了低信噪比下同相轴排齐的问题.使用本文给出的算法处理合成数据和实际资料的结果,验证了该算法分离零偏VSP资料,能够得到具有良好保真性的上、下行波波场,处理效果优于传统SVD法.通过对模型数据的Q值分析可知,与传统SVD法相比,本文给出的方法使Q值估计的准确性获得了明显的提高.这说明该方法不仅能够保真波场的运动学特征,还能良好地保真波场的动力学特征,适合作为Q值分析的预处理步骤.
| [1] | Raoult J J, Joncheray B, Carron D. The check VSP:A new vertical seismic data acquisition and processing technique. 54th Annual SEG Meeting, SEG Expanded Abstracts , 1984: 839-840. |
| [2] | Balch A H, Lee M W, Miller J J, et al. The use of vertical seismic profiles in seismic investigations of the earth. Geophysics , 1982, 47(6): 906-918. DOI:10.1190/1.1441357 |
| [3] | Simaan M. Optimum array filters for array data signal processing. IEEE Trans. of Acoustics Speech and Signal Processing , 1983, 31(4): 1006-1015. DOI:10.1109/TASSP.1983.1164164 |
| [4] | Simaan M, Love P L. Optimum suppression of coherent signals with linear move out in seismic data. Geophysics , 1984, 49(3): 215-226. DOI:10.1190/1.1441654 |
| [5] | 王成礼. VSP多道迭代递归滤波波场分离及应用. 石油地球物理勘探 , 1991, 26(2): 169–178. Wang C L. A method for VSP wave field separation using multitrace iterative recursion filtering, and its application. Oil Geophysical Prospecting (in Chinese) , 1991, 26(2): 169-178. |
| [6] | Freire S L M, Ulrych T J. Application of singular value decomposition to vertical seismic profiling. Geophysics , 1988, 53(6): 778-785. DOI:10.1190/1.1442513 |
| [7] | Rieber F. Visual presentation of elastic wave patterns under various structural conditions. Geophysics , 1936, 1(2): 196-218. DOI:10.1190/1.1437093 |
| [8] | Carswell A, Tag R, Dillistone C, et al. A new method of wavefield separation in VSP data processing. 54th Annual SEG Meeting, SEG Expanded Abstracts , 1984: 40-42. |
| [9] | 朱光明. 垂直地震剖面方法. 北京: 石油工业出版社, 1988 . Zhu G M. Vertical Seismic Profiling (in Chinese). Beijing: Petroleum Industry Press, 1988 . |
| [10] | Blias E. VSP wavefield separation:Wave-by-wave optimization approach. Geophysics , 2007, 72(4): 47-55. |
| [11] | 杜婧, 王尚旭, 刘国昌, 等. 基于局部斜率属性的VSP波场分离研究. 地球物理学报 , 2009, 52(7): 1867–1872. Du J, Wang S X, Liu G C, et al. VSP wavefield separation using local slopes attribute. Chinese J. Geophys. (in Chinese) , 2009, 52(7): 1867-1872. |
| [12] | Gao J H, Yang S L, Wang D X, et al. Estimation of quality factor Q from the instantaneous frequency at the envelope peak of a seismic signal. Journal of Computational Acoustics , 2011, 19(2): 155-179. DOI:10.1142/S0218396X11004390 |
| [13] | Hyvärinen A, Karhunen J, Oja E. Independent Component Analysis. New York: John Wiley & Sons, Inc., 2001 . |
| [14] | Montagne R, Vasconcelos G L. Optimized suppression of coherent noise from seismic data using the Karhunen-Loève transform. Physical Review E , 2006, 74(1): 16213-1. DOI:10.1103/PhysRevE.74.016213 |
| [15] | 凌永祥, 陈明逵. 计算方法教程. 西安: 西安交通大学出版社, 2005 . Ling Y X, Chen M K. A Course in Computational Method (in Chinese). Xi'an: Xi'an Jiaotong University Press, 2005 . |
| [16] | Ganley D C. A method for calculating synthetic seismograms which include the effects of absorption and dispersion. Geophysics , 1981, 46(8): 1100-1107. DOI:10.1190/1.1441250 |
| [17] | 高静怀, 杨森林, 王大兴. 利用VSP资料直达波的包络峰值处瞬时频率提取介质品质因子. 地球物理学报 , 2008, 51(3): 853–861. Gao J H, Yang S L, Wang D X. Quality factor extraction using instantaneous frequency at envelope peak of direct waves of VSP data. Chinese J. Geophys. (in Chinese) , 2008, 51(3): 853-861. |
 2013, Vol. 56
2013, Vol. 56


