2. 东华理工大学放射性地质与勘探技术国防重点学科实验室, 江西抚州 344000
2. Fundamental Science on Radioactive Geology and Exploration Technology Laboratory, East China Institute of Technology, Jiangxi Fuzhou 344000, China
在地震勘探中,地震数据体的采样已达到了五维,数据采集面临着巨大的压力,为了恢复高维的地震数据结构,我们不仅面临奈奎斯特采样定理的限制,而且也面临由于地震数据采集维数的增加而使得数据量呈指数增加的压力[1-2].同时,在野外数据采样过程中,由于野外地形条件或者经济上的限制,地震勘探数据沿空间方向上通常进行不规则采样,在陆地上这种情况可能起因于地震道的布置受到建筑、湖泊、禁采区等复杂地形限制,或者人工放炮不能得到充分的激发,也可能起因于坏道或者严重污染道的出现,从而导致采集到的地震数据不规则、不完整,出现空间假频.在海上地震勘探中,则可能由于电缆的水平偏移等引起,这种稀疏分布的地震数据难以满足高分辨地震勘探的需要[3-4].
近年来提出的压缩感知/采样理论(Compressive sensing/sampling,CS)为解决此类问题提供了新的契机[5],它利用信号的稀疏性,以远低于奈奎斯特采样率的速率对信号进行非自适应测量,从而大大降低采集成本,而将成本转移到数据重建的计算过程中来,从而可以为复杂地区的数据采集、地震道缺失重建、压缩数据采集量以及后续处理做出相应的贡献.但该理论需要满足三个前提条件:一是待处理的信号是稀疏的或者可压缩的,或者至少在某个变换域内满足此条件;二是采用随机欠采样方法,将可能存在的假频混淆现象转化为幅值相对较低的噪声而滤除;三是通过一定的稀疏促进求解策略来求解该问题[6-9].
在压缩感知理论框架下,对于数据采样方式,常用的是纯随机采样,但该采样方式不能控制采样间隔,会造成某些重要信息的缺失,或者不重要信息的聚集,影响数据重建效果,同时也不能根据野外地质环境灵活调整,而后唐刚等[10]引入泊松碟采样方式,提高了重建效果,但该采样方式由于事先固定采样,也不能根据野外地质条件灵活调整,使其在实际应用中有一定局限.Leneman (1966)提出了jitter采样方式[11],首先应用于图像处理,Hennenfent (2008)[12]、唐刚等[13]将其引入到地震数据重建中,使采样点分布相对均匀,在一定程度上能够根据地质条件灵活调整.
对于稀疏促进求解策略,常用方法是基于某种变换,如Radon变换[14-15]、傅里叶变换[2, 16]、curvelet变换[6-7, 17]等,该方法不需要地下结构的先验信息,能够处理规则缺失和不规则缺失地震道的重建,且计算速度快,精度高,目前已经发展到五维地震数据的重建[2, 16],通过利用多维地震数据信息,使得重建效果进一步提高.所采用重建方法主要有最小加权范数方法[16]、抗频谱泄露方法[18]、凸集投影算法[19-20]及谱投影梯度法等[21].而对于凸集投影算法(POCS),其主要思想就是通过多次迭代,去除由随机缺失道所产生的不相干噪声,从而将缺失地震道重建出来.该方法最早由Bregman (1965)提出[22],而后广泛应用于图像处理[23],Abma (2006)将POCS算法应用于不规则地震数据的重建[19],取得了较好的应用效果,在他的文章中,POCS算法每次迭代都需要对时间和空间上进行一次全局正反傅里叶变换,而后Gao (2010)对其进行简化[20],在取得同样效果的前提下,节省部分时间,但是由于以上POCS方法都是基于傅里叶变换,没有研究基于曲波变换的三维数据重建方法,导致只能处理近似线性同相轴的地震数据,并不能很好地反映数据的局部特征,使其数据重建效果有限.况且每次迭代都需要对时间和空间上进行一次全局变换,对计算机内存要求较高,且运算时间较长.我们知道,时间方向上是按照固定的采样率进行采样,不需要进行重建.为此本文在前人研究的基础上,采用具有局部化识别能力的曲波变换作为稀疏表示基[24-25],同时引入新的阈值参数,通过只对时间切片进行处理,降低数据运算的维数,实现基于曲波变换的三维地震数据重建.
2 压缩感知理论 2.1 理论基础地震数据的重建问题可以描述为由一组不完整数据通过线性算子的作用恢复出完整的数据,假设如下线性正演模型:
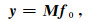
|
(1) |
这里y∈Rn代表采集的地震数据;f0∈RN,且N≥n,表示待重建的无假频数据;M∈Rn×N表示随机采样矩阵,假设数据x0是f0在变换域C中的稀疏表示,则方程(1)可以写成
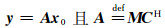
|
(2) |
这里上标H代表共轭转置矩阵.当从采集的数据y中重建无假频数据f0时,由于x0是稀疏的,使得该欠定方程有解.
在稀疏促进反演后,重建信号由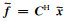
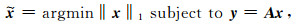
|
(3) |
式中,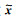
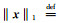
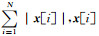
方程(3)中的第一项是稀疏促进项,第二项是为了保持数据的一致性,即通过以上的L1范数最小化,不断促进x的稀疏性,而一致性约束条件y=Ax则保证了该问题的解向真值的方向不断收敛,当通过方程(3)估计出系数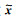
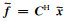
从以上分析可知,压缩感知方法的关键技术之一,是通过最小化策略求解上述欠定问题,为此引入凸集投影算法.假设稀疏变换系数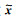
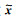
POCS方法步骤为:
(1) 选择阈值参数λi(i=1,2,3,…,N,其中N为迭代次数),初始化y0=y,即输入随机采样得到的地震数据.
(2) 将地震数据yi-1做稀疏变换xi-1=Cyi-1,用λi作为阈值去除小于λi的值,即xi=TλiCxi-1,下标i表示第i次迭代,Tλi表示阈值算子.
(3) 将xi做反稀疏变换

|
(4) |
然后将不完整地震数据y的未缺失地震数据填充到yi上,即
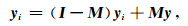
|
(5) |
最后将得到的yi代入步骤(2),重新进行迭代,直到运行N次结束,再对迭代N次后的xn做逆变换即可以得到最终的重建结果.
2.3 阈值参数选取根据压缩感知理论可知,随机欠采样将数据重建问题转化为简单的去噪问题,因此POCS算法重点在于阈值参数λi的选取,不同的阈值参数会获得不同的重建效果,而合适的阈值参数在满足精度要求下,可以减少迭代次数并节省计算成本,在POCS算法迭代过程中,其阈值参数值一般从大到小进行变化,也即大部分曲波系数在前几次迭代进行去除,只留下能量较强的同相轴,而在最后几次迭代中,绝大部分曲波系数保留,只去除一些能量较小的随机噪声,即阈值参数λi满足:
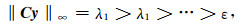
|
(6) |
式中ε为接近零的小值,与数据中噪声的能量有关,不同数据ε值有所差别.在Abma (2006)文章中研究了线性变化递减的阈值参数,该阈值参数λi可由(7)式简单的确定:
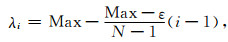
|
(7) |
式中Max为|Cy|的最大值,即稀疏变换系数绝对值的最大值.
Gao等[20]在基于傅里叶变换POCS算法下,对按指数规律衰减的阈值参数进行了研究,并且从理论和实际算例验证该阈值参数重建效果比线性阈值参数效果好,该阈值参数表达式为:
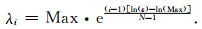
|
(8) |
然而Gao等研究主要采用按照e-x(0≤x≤1)规律衰减的阈值参数,在实际运算中收敛较快,但为了进一步提高收敛速度,本文在此基础上,结合曲波变换,提出选用按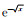
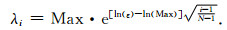
|
(9) |
压缩感知的关键技术之一是随机欠采样方法,因为它可以把混淆真实频率的相干噪声转化成容易滤除的不相干噪声,即使这些随机噪声和真实频谱相互叠合在一起,仍然可以通过迭代的方式检测出真实频率,因此,相干噪声的程度,很自然地就成为衡量一种欠采样方法效果的重要标准之一.然而单纯的随机采样会造成采样点过于聚集或者过于分散的情况,难以达到理想的重建效果,同时也不能根据野外实际地质条件灵活调整,因此引入jitter采样方式,以控制采样间隔,更加适合地震数据重建.jitter采样方法首先将待处理区域划分成若干个子区域,然后在每个子区域内都随机地强制采一个点.由于每个子区域都有采样点,相邻缺失地震道之间的间隔也就得到了控制,同时也保持采样点的随机性,可将假频转化成低幅度噪声,使真实频率更容易检测.
为了说明jitter欠采样策略,假设欠采样因子γ为奇数,例如γ=1,3,5,…,总数据采样点是γ的倍数,致使采集到的样点数为n=N/γ为整数,对于这些选择,可以给出jitter采样点为:
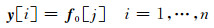
|
(10) |
且
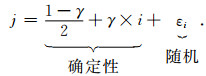
|
(11) |
离散随机变量εi是独立的整数且在-[(ξ-1)/2]和[(ξ-1)/2]采样间隔之间均匀分布,参数ξ称为jitter参数,满足0≤ξ≤γ,主要表示在粗糙网格下jitter的大小,当ξ=γ时,为最优jitter采样.当γ是偶数时也满足,详细推导可以参考文献[11-12].
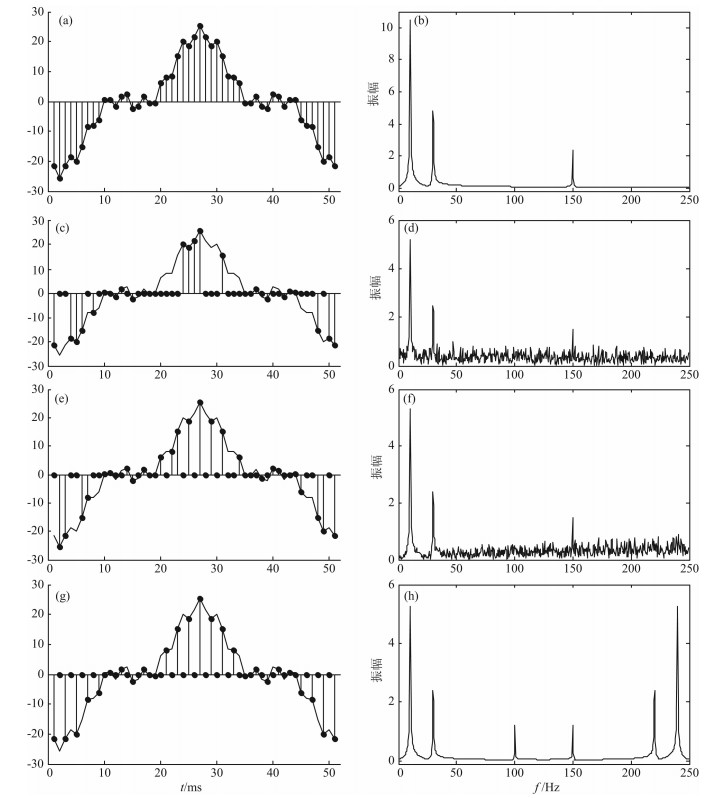
图 1a为三个余弦函数的叠加信号,满足奈奎斯特采样定理进行规则采样,且这个信号在傅里叶域是稀疏的,图 1b为其振幅谱.图 1c为50%随机欠采样,图 1d为其振幅谱,从中可以看出,假频转为不相干的随机噪声,这种情况下,在噪声水平之上的重要信号系数能够通过促进稀疏的去噪技术进行检测,从而精确地恢复出原始信号.这个例子说明如果信号在傅里叶域是稀疏的,可以从较为严重的欠采样中得到良好的恢复.图 1e为50%jitter欠采样,避免了采样间隔过大或者过小,同时也保持采样矩阵的随机性,图 1f为其振幅谱,可以看出信号真实频谱更集中,可以更好地从不相干的噪声中检测出来.图 1g为50%规则欠采样,规则欠采样所引起的假频与真实频谱相似(图 1h),这种情况下,由于在傅里叶域待恢复的信号成分与假频都是稀疏的,且峰值近似相等,因此稀疏促进恢复策略可能失效,也即基于压缩感知理论的数据重建达不到预想效果.这个例子表明对于促进稀疏的重建算法,随机欠采样比规则欠采样更加有利,而jitter欠采样可能比随机欠采样恢复效果更好.
|
图 1 一维(欠)采样方式及其频谱分析 (a)规则采样信号;(c)随机欠采样;(e) jitter采样;(g)规则欠采样.(b)(d)(f)(h)为对应频谱. Fig. 1 Different (under) sampling schemes of 1D and their frequency spectrum (a) Signal regularly sampled above Nyquist rate; (c) Randomly undersampled twofold; (e) Jittered undersampled twofold; (g) Regularly undersampled twofold. The respective amplitude spectra are plotted in (b), (d), (f) and (h). |
由于一维采样方式只沿着一个空间轴的方向采集地震道,重建效果有限,不满足野外数据采集的要求,因此需要发展二维采样方式,沿着两个空间轴方向进行数据采集.对于二维jitter采样而言,其原理与一维jitter采样原理一样,正方形jitter采样公式为:
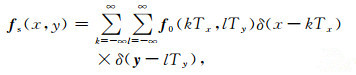
|
(12) |
其中,Tx和Ty分别为x和y方向的采样间隔,δ是连续狄拉克脉冲函数,所有的采样区域都是在指定的平面上进行的,采样函数fs为完整离散数据f0在每个采样位置与脉冲函数的乘积.水平方向和垂直方向的采样间隔可以不相等[11, 13],本文采用Tx=Ty.
待采样区域首先按照上述的正方形网格划分策略分成一系列子块,在每个子块内部,以子块中心为基准,按照一定的jitter偏离率随机地选择一个点,即正方形jitter采样,这种采样一定程度上依赖于子块网格的划分.以子块中心为原点,子块边界至中心距离为γ,偏离中心的jitter参数为ξ,且ξ≤γ.
图 2a为合成地震叠前数据体的某一时间切片模型,满足奈奎斯特采样定理进行规则采样,横坐标表示检波器,纵坐标表示炮点,图 2b为其二维频谱分析,可看出该数据在傅里叶域是稀疏的,满足压缩感知理论要求,图 2c为50%随机欠采样,图 2d为其二维频谱分析,从中可以看出,由于采样矩阵是随机的,引起的假频可以转为不相干的随机噪声,真实频谱可以通过阈值算法进行检测,继而在一定误差范围内恢复出原始数据.图 2e为50%jitter欠采样,图 2f为其振幅谱,可以看出信号真实频谱更为集中,更好地从不相干噪声中检测出来.图 2g为50%规则欠采样,规则欠采样所引起的假频与真实频谱较为接近(图 2h),稀疏促进恢复策略会受到一定影响.

|
图 2 二维(欠)采样方式及其f-k谱 (a)规则采样;(c)随机欠采样;(e) jitter采样;(g)规则欠采样.(b)(d)(f)(h)为对应的f-k谱. Fig. 2 Different (under) sampling schemes of 2D and f-kspectrum (a) Signal regularly sampled above Nyquist rate; (c) Randomly undersampled twofold; (e) Jittered undersampled twofold; (g) Regularly undersampledt wofold. The respective f-k spectra are plotted in (b), (d), (f) and (h). |
为了更好地对比数据重建效果,定义信噪比SNR=20log10‖x0‖2/‖x-x0‖2,单位为dB,其中x0表示原始模型数据,x表示重建结果,信噪比越高,代表重建结果与模型数据越接近,效果越理想,同时本文在三维地震数据重建过程中,曲波变换的尺度数为6,最粗尺度上的角度数为8.
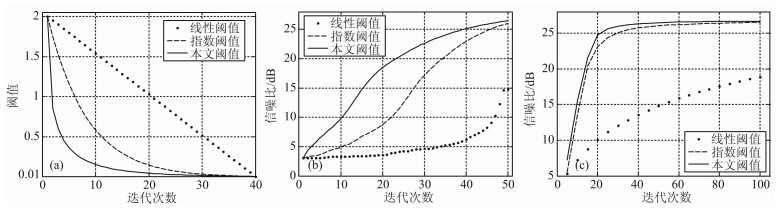
图 3a为线性阈值、指数阈值和本文提出的阈值参数曲线图,其中Max=2,ε=0.01,图中可以看出本文提出的阈值参数在相同迭代次数下衰减速率最快,线性阈值参数衰减速率最慢.然后利用本文方法,采用三种不同的阈值参数对理论模型50%欠采样后的数据(图 2c)进行数据重建.图 3b为迭代次数100次时,迭代次数与不同阈值参数重建后信噪比关系曲线图,可以看出每次迭代过程中本文提出的阈值参数重建后信噪比最高,其次是指数阈值参数,最后才是线性阈值,同时将最大迭代次数从5~100次变化,计算出每次最大迭代次数与重建后信噪比关系曲线图,如图 3c所示,从中可以看出,不同最大迭代次数中,本文提出的阈值参数重建后信噪比最大,而且也可以看出,要想获得信噪比为16dB的重建结果,线性阈值需迭代60次左右,指数阈值需迭代12次左右,而本文提出的阈值参数只需迭代9次左右,可以节省一定的计算时间.总体而言三种阈值参数重建后的信噪比都随迭代次数的增大而增加,但迭代次数太多会浪费计算时间,需要进行折衷考虑.而对于指数阈值和本文阈值参数,当迭代次数大于30次后,信噪比增加量随迭代次数增加相对较少,但为了突出效果,本文后续的理论模拟选用迭代次数为40次.
|
图 3 阈值参数及其重建信噪比曲线图 (a)阈值参数示意图;(b)迭代次数100时,迭代次数与信噪比图;(c)迭代次数不同时,迭代次数与信噪比图. Fig. 3 Schematic diagram of threshold parameter and SNR after data reconstruction (a) Schematic diagram of threshold parameter; (b) Schematic diagram of iterations and SNR at fixed 100 iterations; (c) Schematic diagram of iterations and SNR at different iterations. |
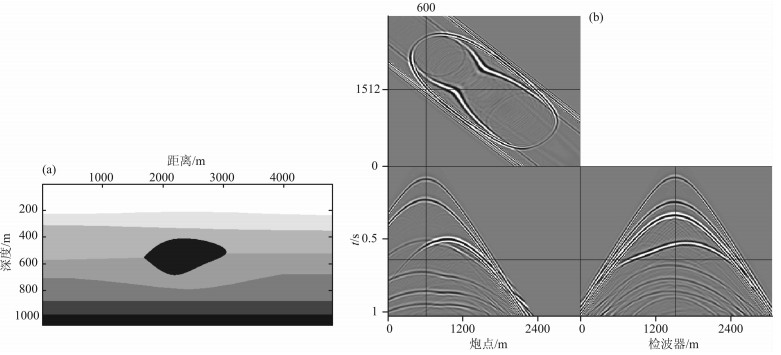
为了更详细阐述基于jitter采样和曲波变换的三维地震数据重建方法,建立一个地下二维不均匀速度模型(图 4a),采用声波有限差分方法,模拟出均匀网格采样下的地震正演记录,采用256道检波器进行接收且检波器固定不变,检波器位置从800m到3860m,道距为12m,炮点从第一个检波器开始,依次移动一个道距进行放炮,共256炮,时间采样间隔为4ms,对所得到的正演地震数据按检波器、炮点以及时间进行排列成三维数据体.由于本文方法在时间方向不需要进行重建,因此三维地震数据重建实际为二维空间方向的数据重建,为此只需对抽取出来的时间切片进行处理,模拟炮点和检波点随机欠采样过程,理想采样数据如图 4b所示,其中时间切片为0.6s,共炮点对应距离为1512m (127炮),共检波点对应的距离为600m (51道),图 2b为其时间切片f-k谱.
|
图 4 简单盐层构造模型(a)及其模拟地震记录(b) Fig. 4 (a) The simplified model of a salt structure and (b) simulation seismic record |
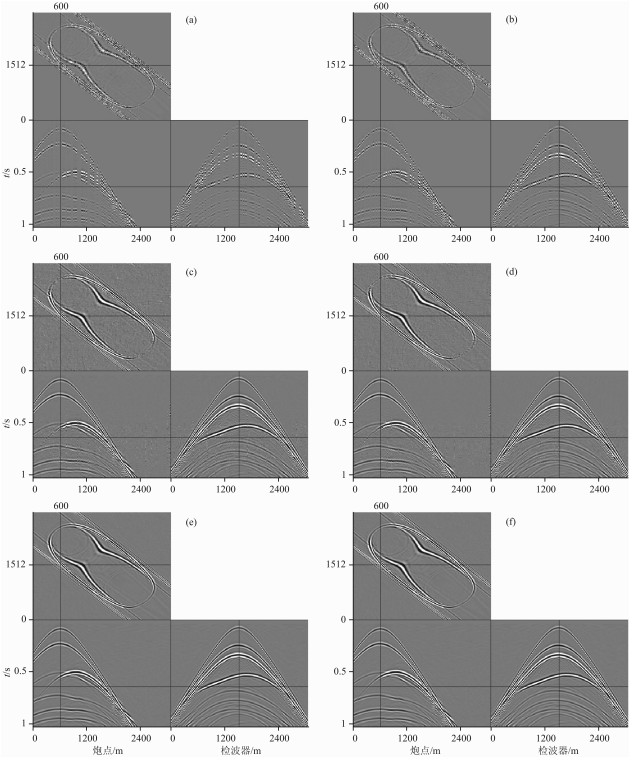
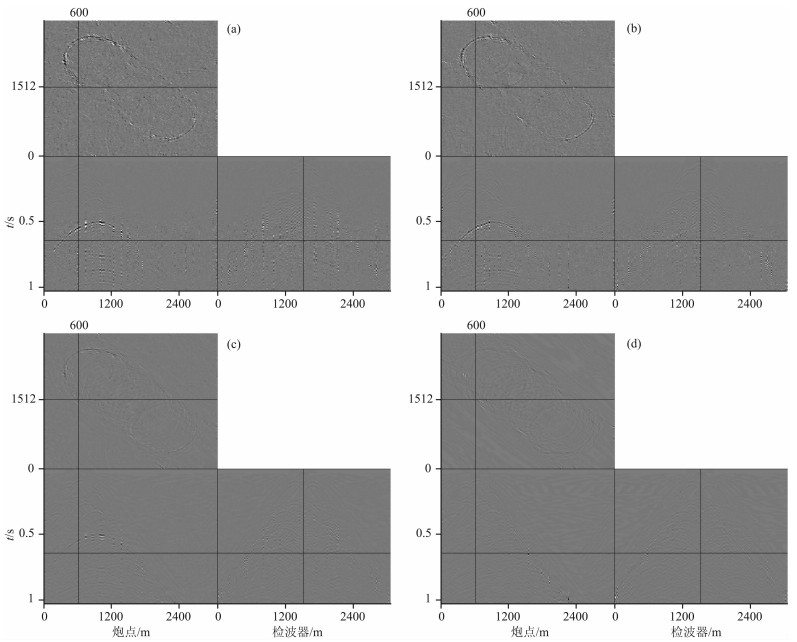
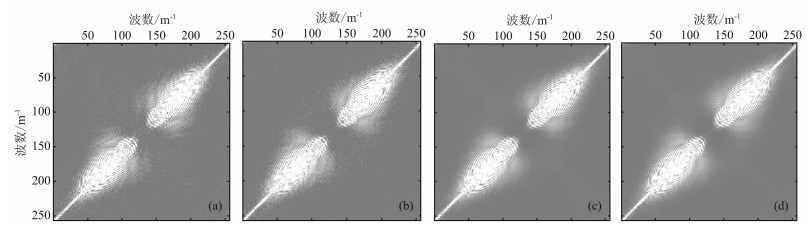
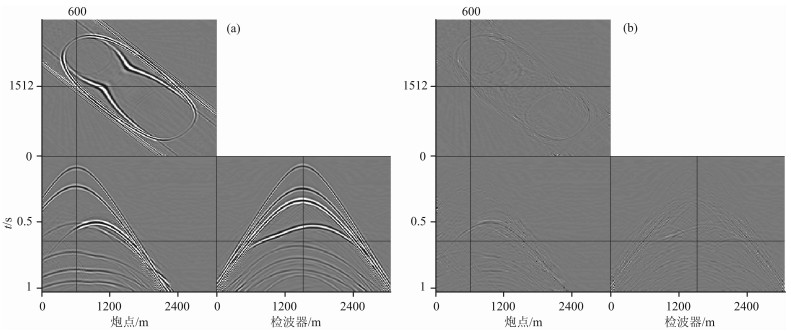
由于一维欠采样的数据重建只利用一个方向的信息,重建效果有限,所以需要发展多维采样方法,增加其它方向的信息,为此,对时间切片模型进行50%二维随机欠采样与50%二维jitter欠采样,欠采样结果如图 5a和图 5b所示,其实际切片f-k谱见图 2d与图 2f.为了显示曲波变换作为稀疏基的优越性,同时也选用傅里叶变换对欠采样数据进行处理,图 5c和图 5d为选用傅里叶变换对二维随机欠采样和二维jitter欠采样后的数据重建结果,重建后信噪比分别为16.62dB和18.03dB,图 5e和图 5f为选用曲波变换的重建结果,重建后信噪比分别为25.26dB和26.16dB.值得一提的是由于只采用50%欠采样,所以jitter欠采样与随机欠采样重建后的信噪比相差不是特别大,如果更低的欠采样,那么重建后信噪比差别较大,不过从另外一个方面可以反映出曲波变换的优越性,即对于间隔较大的采样点重建效果仍然较好.图 6a-6d为重建后的地震记录与原始地震记录的差值剖面,从中可以看出选用曲波变换作为稀疏基的数据恢复效果远优于傅里叶基,重建后的能量损失较小,同时jitter欠采样由于控制了最大采样间隔,因此重建效果也优于随机欠采样后的重建效果,图 7a-7d分别为选用傅里叶变换和曲波变换对随机欠采样和jitter欠采样重建后时间切片的f-k谱,可以看出,图 7a与图 7b的f-k谱不光滑,有较小的频谱泄漏,而图 7c与图 7d的-fk谱更光滑,相比之下,图 7d更接近于原始时间切片的频谱,因此可以得出,在二维jitter欠采样下,基于曲波变换的三维地震数据重建效果最优.为了进一步体现本文方法的优越性,特意选用基于曲波变换的谱梯度投影算法进行重建对比[21],考虑到对比效果的公平,该方法也调试到最好的重建效果.图 8a为采用谱梯度投影算法对图 5b的重建结果,重建后信噪比为23.11dB,图 8b为其误差剖面图.同时从计算时间来看,谱梯度投影算法计算时间为POCS算法的5倍,因此可以得出,本文方法在用时少的情况下,其重建效果也比谱梯度投影算法要好.
|
图 5 二维欠采样及其重建结果(50%地震道缺失) (a)二维随机欠采样;(b)二维jitter欠采样;(c)傅里叶基对(a)重建结果,SNR=16.62dB;(d)傅里叶基对(b)重建结果,SNR=18.03dB;(e)曲波基对(a)重建结果,SNR=25.26dB;(f)曲波基对(b)重建结果,SNR=26.16dB. Fig. 5 2D undersampling schemes and reconstruction results (50% missing traces) |
|
图 6 二维欠采样重建误差图(50%地震道缺失) (a)图 5c误差图;(b)图 5d误差图;(c)图 5e误差图;(d)图 5f误差图. Fig. 6 Reconstruction residuals of 2D undersampling scheme (50% missing traces) |
|
图 7 二维欠采样重建结果的f-k谱 (a)-(d)分别为图 5c-5f的f-k谱. Fig. 7 The f-k spectrum of 2D undersampling scheme reconstruction results (a)-(d) is the f-k spectrum of Figs.5c-5f respectively. |
|
图 8 谱梯度投影算法重建结果及误差图(50%地震道缺失) (a)谱梯度投影算法重建结果,SNR=23.11dB;(b)图 8a误差图. Fig. 8 Result and reconstruction residuals of spectral projected-gradient (50% missing traces) |
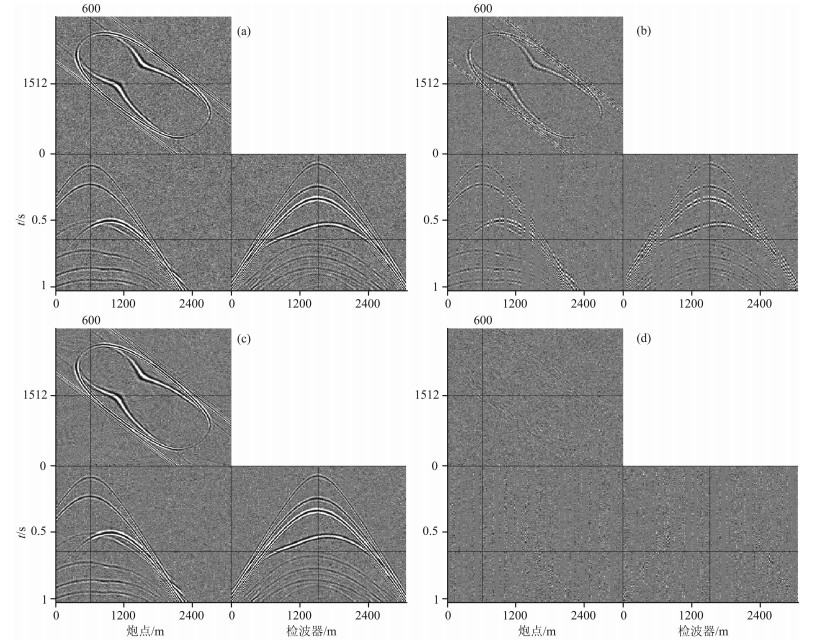
由于地震数据通常都含有噪声,所以需要检验jitter欠采样下凸集投影重建算法的抗噪声能力.在图 4b模型中加入高斯随机噪声,如图 9a所示,然后进行抗噪重建模拟试验,图 9b为50%二维jitter欠采样剖面图,图 9c为jitter欠采样下的重建结果,信噪比为11.41dB,图 9d为重建前后的误差剖面.通过对比可以看出,重建后的有效信息几乎不变,数据重建效果较好,这也说明采用曲波变换作为稀疏基的凸集投影算法在地震数据重建中,具有良好的抗噪声能力,能够运用于实际资料.
|
图 9 二维含噪数据jitter欠采样及其恢复结果(50%地震道缺失) (a)加噪地震数据;(b)二维jitter欠采样;(c)由图(b)重建结果,SNR=11.41dB;(d)图 9c误差图. Fig. 9 Jittered undersampling from the noise data and reconstruction results (50% missing traces) |
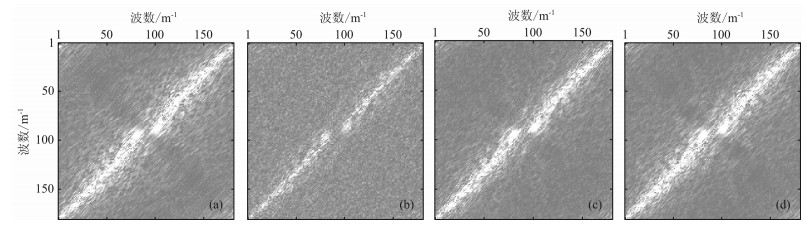
某海上二维高密度地震资料道距25m,采样率4ms,180道接收,检波点和炮点每次都移动一个检波器距离,我们按照检波器、炮点以及时间进行排列成三维数据体,为了减少运算时间,截取了中间180道×180炮以及采样长度2s的数据进行处理,图 10a为时间切片为1.2s,共炮点距离与共检波点距离都为2250m的理想采样数据,图 10b为对理想采样记录进行50%二维jitter欠采样,然后利用凸集投影算法进行重建,图 10c为基于曲波变换的谱梯度投影算法重建结果,重建后SNR=7.32dB,图 10d为本文方法重建结果,重建后SNR=8.71dB.可以看出,在采样50%的情况下,两种方法重建效果都较好,但本文方法效果更优,其局部细节信息得到了更好的恢复,同相轴几乎与原始地震记录一样,同时计算的效率也更高,能够满足后续处理的要求.图 11为图 10数据时间切片的f-k谱,从中也可以看出,本文方法重建后f-k谱与真实频谱最为接近,并且重建过程起到了一定的去噪作用.

|
图 10 二维欠采样及其重建结果(50%地震道缺失) (a)原始地震数据;(b)二维jitter欠采样;(c)谱梯度投影重建结果,SNR=7.32dB;(d)本文方法重建结果,SNR=8.71dB. Fig. 10 2D undersampling scheme and reconstruction results (50% missing traces) |
|
图 11 原始数据欠采样及重建结果的f-k谱 (a)-(d)分别为图 10a-10d的f-k谱. Fig. 11 The f-k spectrum of data undersampling and reconstruction results (a)-(d) is the f-k spectrum of Figs.10a-10d respectively. |
本文主要在压缩感知理论的基础上,研究了基于曲波变换的三维地震数据重建方法,提出了新的阈值参数,并引入了jitter欠采样方式,改善单纯的随机采样.数值试验和实际应用表明,jitter欠采样在保持采样随机性的同时,使采样点的分布更加均匀,进一步提高地震数据的重建效果,然而jitter欠采样也不是最佳采样方式,不能完全根据野外地质环境进行灵活调整,该采样方式只是提供一种思路,即在实际数据采集过程中,尽量使采样点间隔不要太大,同时又保持随机性,否则将影响后续的重建效果,然而在实际勘探中可能事先知道某些区域的先验地质信息,因此下一步需要研究构建基于先验地质信息的采样方式.
从本文的重建结果可以看出,使用曲波变换作为稀疏基后,数据重建效果有较为明显的改进,但与傅里叶基相比,运算时间增加近20倍左右,使得在地震海量数据的应用中受到一定限制,因此也需要发展其它有效快速算法,在确保重建精度的同时减少运算时间.同时目前曲波变换方法研究前提是数据采样网格为均匀,而在野外实际施工时,由于地形条件的限制或者海上电缆水平偏移,数据采样网格很多情况下是非均匀的,因此发展基于非均匀曲波变换的地震数据重建方法也是今后研究的重要内容.
致谢衷心感谢中国石油大学(北京)地球物理与信息工程学院马继涛博士、刘国昌博士为本文分别提供的理论数据和实际数据,以及在科研中给予的帮助与指导.
| [1] | Herrmann F J. Randomized sampling and sparsity:Getting more information from fewer samples. Geophysics , 2010, 75(6): WB173-WB187. DOI:10.1190/1.3506147 |
| [2] | Trad D O. Five-dimensional interpolation:Recovering from acquisition constraints. Geophysics , 2009, 74(6): V123-V132. DOI:10.1190/1.3245216 |
| [3] | 马坚伟, 唐刚, 汤文.基本曲波变换和压缩感知的不完备地震数据恢复.长沙:中国地球物理年会, 2010. Ma J W, Tang G, Tang W. Recovery of incomplete seismic data based on curvelet transform and compressed sensing (in Chinese). Changsha:Chinese Geophysical Year Meeting, 2010. http://www.oalib.com/references/18986342 |
| [4] | 孟小红, 郭良辉, 张致付, 等. 基于非均匀快速傅里叶变换的最小二乘反演地震数据重建. 地球物理学报 , 2008, 51(1): 235–241. Meng X H, Guo L H, Zhang Z F, et al. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform. Chinese J. Geophys. (in Chinese) , 2008, 51(1): 235-241. |
| [5] | Donoho D L. Compressed sensing. IEEE Transactions on Information Theory , 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [6] | Herrmann F J, Hennenfent G. Non-parametric seismic data recovery with curvelet frames. Geophysical Journal International , 2008, 173(1): 233-248. DOI:10.1111/gji.2008.173.issue-1 |
| [7] | Herrmann F J, Wang D, Hennenfent G, et al. Curvelet-based seismic data processing:A multiscale and nonlinear approach. Geophysics , 2008, 73(1): A1-A5. DOI:10.1190/1.2799517 |
| [8] | Neelamani R, Baumstein A, Gillard D, et al. Coherent and random noise attenuation using the curvelet transform. The Leading Edge , 2008, 27(2): 240-248. DOI:10.1190/1.2840373 |
| [9] | Wason H, Herrmann F J, Tim T Y. Sparsity-promoting recovery from simultaneous data:a compressive sensing approach. 81th Annual International Meeting of Society of Exploration Geophysicists, 2011:6-10. http://www.oalib.com/references/18986332 |
| [10] | 唐刚, 杨慧珠. 基于泊松碟采样的地震数据压缩重建. 地球物理学报 , 2010, 53(9): 2181–2188. Tang G, Yang H Z. Seismic data compression and reconstruction based on Poisson disk sampling. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2181-2188. |
| [11] | Leneman O. Random sampling of random processes:Impulse response. Information and Control , 1966, 9(2): 347-363. |
| [12] | Hennenfent G, Herrmann F J. Simply denoise:wavefield reconstruction via jittered undersampling. Geophysics , 2008, 73(3): V19-V28. DOI:10.1190/1.2841038 |
| [13] | 唐刚.基于压缩感知和稀疏表示的地震数据重建与去噪.北京:清华大学, 2010. Tang G. Seismic data reconstruction and denoising based on compressive sensing and sparse representation (in Chinese). Beijing:Tsinghua University, 2010. http://www.oalib.com/references/19466063 |
| [14] | Trad D, Ulryeh T, Sacchi M. Latest views of the sparse Radon transform. Geophysics , 2003, 68(1): 386-399. DOI:10.1190/1.1543224 |
| [15] | Wang J F, Ng M, Perz M. Seismic data interpolation by greedy local Radon transform. Geophysics , 2010, 75(6): 225-234. |
| [16] | Jin S. 5D seismic data regularization by a damped least-norm Fourier inversion. Geophysics , 2010, 75(6): 103-111. DOI:10.1190/1.3505002 |
| [17] | 刘国昌, 陈小宏, 郭志峰, 等. 基于curvelet变换的缺失地震数据插值方法. 石油地球物理勘探 , 2011, 46(2): 237–245. Liu G C, Chen X H, Guo Z F, et al. Missing seismic data rebuilding by interpolation based on curvelet transform. Oil Geophysical Prospecting (in Chinese) , 2011, 46(2): 237-245. |
| [18] | Xu S, Zhang Y, Pham D, et al. Antileakage Fourier transform for seismic data regularization. Geophysics , 2005, 70(4): 87-95. |
| [19] | Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm. Geophysics , 2006, 71(5): E91-E97. |
| [20] | Gao J J, Chen X H, Li J Y, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method. Applied Geophysics , 2010, 7(3): 229-238. DOI:10.1007/s11770-010-0246-5 |
| [21] | Berg E D, Friedlander M P. Probing the Pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. , 2008, 31(2): 890-912. |
| [22] | Bregman L. The method of successive projection for finding a common point of convex sets. Soviet Math , 1965, 6(3): 688-692. |
| [23] | Ozkan M K, Tekalp A M, Sezan M I. POCS based restoration of space-varying blurred images. IEEE Transactions on Image Processing , 1994, 3(4): 450-454. DOI:10.1109/83.298398 |
| [24] | Candès E, Demanet L, Donoho D, et al. Fast discrete curvelet transforms. SIAM Multiscale Modeling and Simulation , 2006, 5(3): 861-899. DOI:10.1137/05064182X |
| [25] | Ma J, Plonka G. The curvelet transform. IEEE Signal Processing Magazine , 2010, 27(2): 118-133. DOI:10.1109/MSP.2009.935453 |
 2013, Vol. 56
2013, Vol. 56

