2. 中国石油吉林油田勘探开发研究院, 松原 138003
2. Jilin Oilfield, CNPC, Songyuan 138003, China
地震数据插值是地震资料处理流程中的重要环节之一.在理想观测系统中,炮点和检波点被设计在规则位置上,但在实际数据采集过程中,时常发生丢失数据的现象(例如,海上勘探中近炮检距数据的缺失,陆上勘探中的坏道以及被噪声严重干扰的地震道).近些年,三维地震勘探方法的快速发展极大增加了采集的数据量,但是数据采集过程中空间维数的增加使得获取规则地震数据体的任务变得更加困难.在海上勘探中,水上采集拖缆由勘探船拖引,这种方式导致了不规则的炮检距-方位角分布.此外,大炮检距的数据采集位置常常被拖缆的漂移(羽状现象)所影响.在陆上勘探观测系统中有更多不可预料的情况发生,由于一些实际环境和经济因素的考虑,很少获取完整的三维覆盖数据体.非规则的数据分布往往引起空间假频现象,加剧了处理过程中假象的产生.地震数据插值是很多重要数据处理技术应用的前提.例如,克希霍夫叠前深度偏移[1]、海上数据三维表层相关多次波消除技术(SRME)[2]、三维波动方程偏移(WEM)[3]和四维时移地震勘探的可重复性处理[4]等.
在实际地震勘探中,很多数据插值方法已经得到了应用.例如,最简单的面元重置方法.但这种方法会产生假象,并且最终导致偏移成像失败.带有部分正常时差校正(NMO)的面元重置方法可以对炮点和检波点位置的微分时差进行校正,产生较好的处理效果,但是,这些方法仍然受过于简单的NMO假设所制约.另外一类方法是基于不同类型的积分连续算子,例如:炮检距连续和炮点连续等.积分连续算子可以直接应用于缺失数据的插值问题[5-7],但在计算炮检距空间内的小距离连续时,由于积分孔径有限,处理效果有时不是很理想.数据插值问题可以作为迭代最优化问题利用褶积算子进行求解[8],这种方法在处理大的数据间隔时具有较高的效率,但是,非平稳同相轴使该方法面临很大的挑战,尽管非稳态预测滤波器可以带来比较精确的处理结果,但是由于需要调节大量的参数,而使得该方法的应用得到了很大的限制.分形插值数据重建方法[9]能够很好地恢复地震数据的局部信息,但是有时存在一定的计算效率问题.基于干涉测量的地震数据重建方法[10]主要利用地震数据的可预测特性,但效果有时受限于有限的记录孔径.基于非均匀离散Fourier变换[11-13]以及Radon变换[14-15]的数据插值方法具有很好的计算特性,但是这些方法有时不能很好地解决空间假频问题.
压缩感知(Compressivesensing)是由Candés[16]和Donoho[17]在信号处理领域正式提出的概念,根本条件是信号本身具有可压缩性.该理论在很多领域得到了广泛的应用,其中也为地震数据插值问题带来了解决方案.近年来,结合Fourier变换[18-20]和curvelet变换[21-22]的稀疏反演方法在处理地震数据插值问题时取得了较好的效果,其理论基础都源于压缩感知理论.不过由于这些数学变换都不是特殊针对地震数据开发的方法,因此并不能为地震数据提供最佳的稀疏表征,在解决地震数据(尤其含空间假频情况)插值问题时,仍然存在一定的限制.类小波变换是小波变换研究领域发展的新方向,在图像处理和数据分析中具有广泛的应用,其主要利用数据的方向特性进行分析.Fomel和Liu[23]开发了一种针对地震数据方向性的seislet变换.刘洋等[24]开发了seislet变换的高阶形式,能够对沿同相轴方向的复杂信号(例如,具有AVO效应的地震同相轴)进行有效地压缩,该特性被应用于随机噪声的衰减问题.Liu和Fomel[25]进一步扩展seislet变换,通过结合炮检距连续(offset continuation,OC)算子,开发了OC-seislet变换方法,并用于解决存在散射波场的噪声衰减及数据插值问题.但是,地震数据的空间假频问题仍然很难被现有的seislet变换所解决,因此,研究能够表征含空间假频地震信号的改进型seislet变换方法,具有重要的理论价值.
本文从小波变换的提升算法出发,结合变尺度平面波分解滤波器表征的非稳态反假频地震倾角,开发seislet变换的反假频形式,提高该变换表征含有空间假频地震数据的能力,利用压缩感知理论开发出反问题计算方法,为有效解决存在空间假频现象的地震数据插值问题提供了一种快速的迭代方法.
2 理论基础 2.1 反空间假频Seislet变换Seislet变换[23]是一种针对地震数据开发的类小波变换方法,可以提供比经典小波变换更加有效的地震数据压缩能力.该变换方法通过结合地震数据预测和离散小波变换提升算法(附录A),改进公式(A1和A3)中的预测算子和公式(A2和A4)中的更新算子,实现表征针对地震数据的稀疏变换.在离散小波变换中,变换的基本单元是数据样点,而在seislet变换中,对应的处理单元是地震道,根据地震道中局部倾角属性对同相轴进行预测和时移,对地震同相轴进行校正后的数据符合离散小波变换的分片平滑假设.
假设地震剖面为s,地震道的集合s=[s1 s2…sN]T,其中N为地震总道数,si为第i道地震数据,其时间样点数设为M.平面波分解算子[26]是一种非稳态预测误差滤波器,其定义为
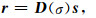
|
(1) |
其中,r为残差,σ为时间和空间变化的局部地震倾角,D为分解算子且有如下定义:

|
(2) |
其中,I代表单位算子,Pi,j(σi)为从第i道到第j道的预测因子,可由Fomel[26]给出的方法算出.地震道的预测过程是原始地震道沿主地震倾角方向的时移运算.对预测误差r求极小值提供了一种计算倾角的方法.
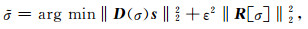
|
(3) |
其中,ε为正则化因子,R[]为正则化算子,可以选择Tiknovo正则化方法[27]或者整形正则化方法[28],正则化条件限制倾角在数据空间中平滑分布.此时道间预测因子Pi,j(σi)也已知,相距较远的地震道之间预测过程可以由简单的递归来实现,例如,从第1道到第k道的预测为
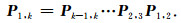
|
(4) |
通过使用平面波预测因子Pk,可以对提升算法的预测算子和更新算子进行修改.例如,对于CDF5/3小波系数,可以得到seislet变换中对应的预测算子P和更新算子U:

|
(5) |

|
(6) |
其中,Pk(+)和Pk(-)为一个地震道的左右方向预测因子,该预测因子是地震倾角的函数,主要根据局部地震倾角对地震同相轴进行时间方向的移动来实现预测[26].如果要解决空间假频的问题,需要设计可以反假频的预测因子,即从根本上求取可以反假频的地震倾角.
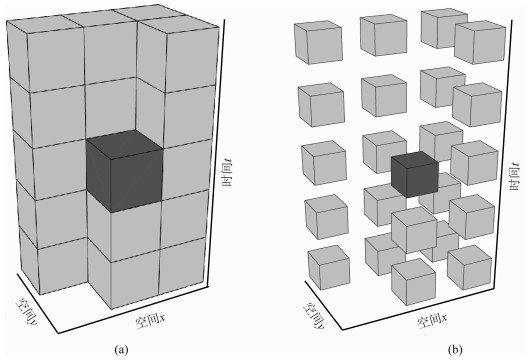
由于空间假频是空间方向采样不足所造成的,因此如果使用数据自身的时间和空间采样率将会使假频影响到地震倾角的准确性,图 1a为三维预测误差滤波器示意图,同时改变时间和空间方向的采样比例(即在各方向滤波器系数之间插入零值,使滤波器能够计算更大尺度的数据),通过预测误差滤波器具有的尺度缩放不变性[29-30],能够有效地解决假频数据的预测,如图 1b所示.
|
图 1 三维预测误差滤波器的反假频原理图[29] (a)原始预测误差滤波器;(b)尺度缩放后的预测误差滤波器. Fig. 1 Antialiasing illustration of 3D prediction-error filter[29] (a) Original prediction-error filter; (b) Prediction-error filter after rescaling. |
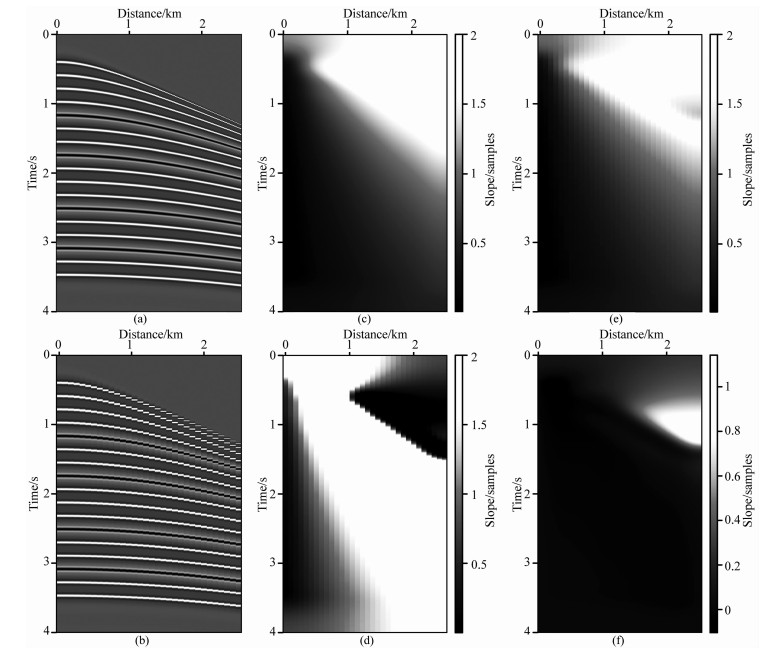
为了测试该方法的反假频能力,建立一个多层反射模型(图 2a),该理想双曲线模型由时变速度通过反向NMO生成.对图 2a的空间方向进行每4道取1道采样,抽样后的结果如图 2b所示.从图中可以看到,由于空间方向的采样不足,造成原有连续的同相轴在远炮检距位置出现了台阶效应,即表现为空间方向的假频.图 2c是对图 2a应用平面波分解滤波器计算的倾角结果,可以看到,该方法能够准确地计算倾角.在浅层远炮检距位置由于无地震数据而产生零空间,该区域的倾角值由正则化算子决定,因此所产生的数值并不是真实的倾角值,但由于该区域数据为零,所以并不影响构建数据预测.应用不带反假频参数的平面波分解滤波器计算图 2b的倾角,结果如图 2d所示,可以看到空间的稀疏采样使计算的倾角产生了较大的误差.带有反假频参数的平面波分解滤波器计算的倾角结果如图 2e所示,对比图 2c和图 2e,可以看到除空间采样不同外,倾角的数值具有很好的相似性.对图 2e进行本质无震荡(ENO)道间插值后,计算与图 2c的差异,如图 2f所示.差异倾角的数值在有效数据区域内小于0.2,说明反假频平面波分解滤波器能够准确地计算真实地震倾角.反假频seislet变换的建立为压缩感知理论解决地震数据插值问题提供了必要的稀疏变换.
|
图 2 反假频倾角测试 (a)理论模型;(b)空间抽样后的理论模型;(c)图 2a的倾角结果;(d)图 2b的倾角结果(无反假频);(e)图 2b的倾角结果(带反假频);(f)图 2c与图 2e经过ENO道间插值结果的差异倾角. Fig. 2 Tests of antialiasing dip calculation (a)Theoretical model; (b) Model after spatial subsampling; (c) Local dip of Fig. 2a; (d) Local dip of Fig. 2b without antialiasing parameters; (e) Local dip of Fig. 2b with antialiasing parameters; (f) Difference between Fig. 2c and Fig 2e. |
地震数据插值问题可以看作一类线性估计问题[31],表达式为
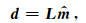
|
(7) |
其中,d为观测数据,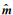
缺失数据插值是一类特殊的数据规则化问题,此时已知的数据已经在规则的观测系统网格里,只需要恢复在空面元内的缺失数据即可.选取L为选择算子K(对角矩阵,已知数据处为1,缺失数据处为0),此时公式(7)为欠定问题,需要增加额外的正则化条件.压缩感知是在信号处理领域正式提出的概念,根本条件是信号本身具有可压缩性,其理论基础要求从数据空间对模型空间进行投影,并且模型空间的系数只有少数元素为非零,即具有稀疏的特性.建立数据空间和模型空间的关系需要通过某种数学变换(例如,比较常用的Fourier变换和小波变换,本次研究中选取反假频seislet变换)来完成.该理论在很多领域得到了广泛的应用,其中也为地震数据插值问题带来了解决方案.本次研究结合反假频seislet变换,提出一种快速、准确的迭代数据插值算法.不同于L2准则,压缩感知理论利用稀疏反变换算子(如反假频seislet反变换算子T)建立一个稀疏的数据空间m(其中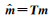
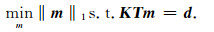
|
(8) |
公式(8)是一个凸规划问题,可以利用线性算子进行求解,然而该问题依赖于矩阵KT的结构,当矩阵KT为大型密集矩阵,同时d中包含噪声的条件下,往往将约束问题转化为如下非约束问题进行求解:
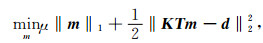
|
(9) |
其中,μ为惩罚参数.许多学者提出了不同的算法用于解决非约束最小二乘问题,如凸集投影方法(POCS)[18].然而,公式(8)与公式(9)并非完全等价,为了满足KTm=d的条件,μ需要取为较小值,此时,正则化条件‖m‖1的限制作用趋于无效.一种解决方法是在迭代求解过程中,使μ从大到小变化[32],但是该方法使得收敛速度变慢.
Bregman迭代方法是Osher等2005年在图像处理领域提出的方法[33],不同于只求解一次公式(9),Bregman迭代求解一系列凸问题[34],Bregman的迭代框架为
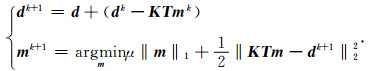
|
(10) |
Bregman迭代方法的优势在于,公式(10)中的参数μ为常数,所以该方法确保了迭代最优化方法的快速迭代.求解公式(10)中的非约束子问题可以利用迭代软阈值方法[35],通过结合稀疏正变换算子(如反假频seislet正变换算子T-1),用于解决数据插值问题的Bregman迭代方法为:
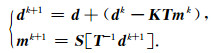
|
(11) |
其中,S[]为软阈值算子[36].
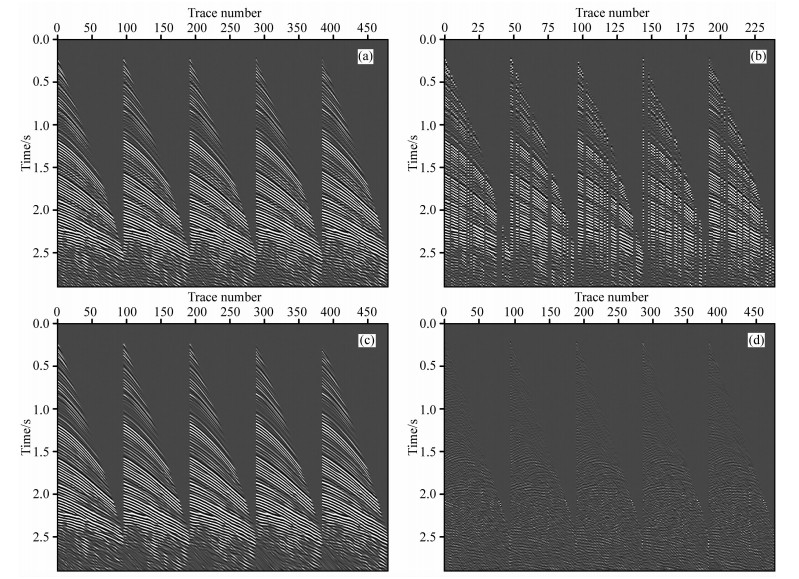
3 理论模型分析为了验证反假频seislet变换的插值效果,使用标准Marmousi模型进行测试,图 3a显示选取的5炮记录,共480道.首先对该数据进行隔道抽样(抽样后为240道),此时由于空间采样不足,数据出现空间假频,接下来将抽样后数据随机去掉30%的地震道,如图 3b所示.应用带有反假频的平面波分解滤波器可以求得图 3b的反假频倾角,对该倾角数据进行ENO道间插值并且通过结合提升算法,即可构建能够表征带有空间假频地震数据的稀疏seislet正反变换,最后利用Bregman迭代算法(公式11),能够对缺失的地震数据进行恢复,如图 3c所示,从该图中难以区分插值数据和原有数据.图 3d为理想数据(图 3a)和插值结果(图 3c)的差异剖面,可以看到,二者的差异较小,只有一些大倾角的同相轴能量未被完全恢复.
|
图 3 理论模型 (a)Marmousi模型炮记录;(b)隔道抽样并且随机去掉30%数据的炮记录;(c)本文方法插值结果;(d)差异剖面. Fig. 3 Synthetic models (a) Shot gathers from Marmousi model; (b) Seismic data with subsampling and 30% randomly selected traces removed; (c) Interpolated result using proposed method; (d) Difference section between figure 3a and 3c. |
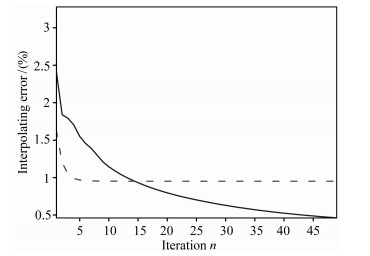
为了验证Bregman迭代方法(公式11)的计算效率,选取凸集投影(POCS)方法[18]进行对比,针对图 3中理论模型进行处理,两种迭代算法使用相同的反假频seislet变换和相同参数的软阈值参数.计算两种方法的插值误差与理想记录(图 3a)的相对误差百分比,如图 4所示.其中,实线为Bregman迭代方法,虚线为POCS迭代方法.从图中可以看到,尽管POCS的前5次迭代收敛速度较快,但是随着迭代次数的继续增加,插值误差保持在较大的误差水平(约1%),而Bregman迭代方法随着迭代次数的增加,误差也一直递减,在50次迭代以后,误差达到了比较合理的水平(小于0.5%).在Bregman和POCS算法的单次循环中,两种方法都只包括1次seislet正变换和1次seislet反变换,而不同是数据空间的加减运算,但是其计算时间相对seislet正反变换而言较小,可以认为两种方法的单次循环计算时间近似相等,因此验证Bregman迭代方法具有更高的计算效率.
|
图 4 计算效率比较(实线为Bregman迭代,虚线为POCS迭代) Fig. 4 Comparison of computation cost (solidl ine; Bregman iteration, dashline; POCS iteration) |
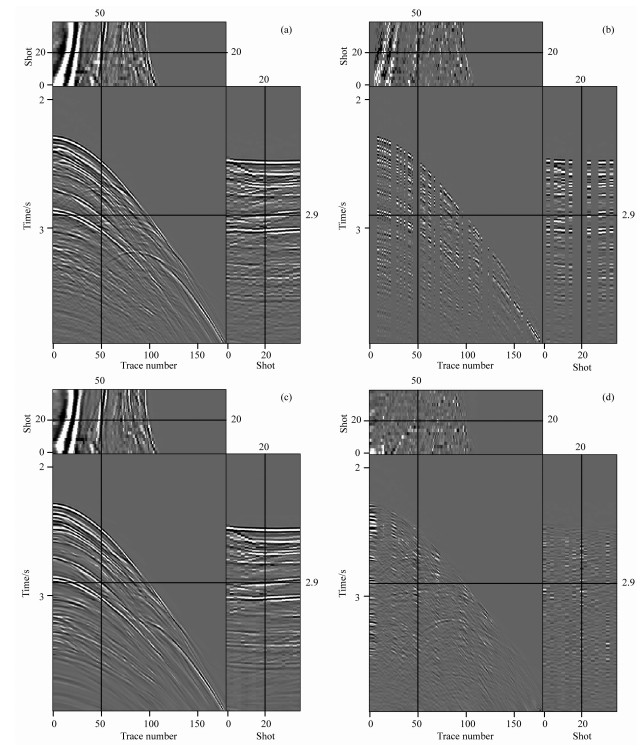
在实际资料处理中,选取墨西哥湾深海某地区炮记录,如图 5a所示.该记录每个单炮共180道.图中三个截面分别为:左上截面为2.9s位置的时间切片,左下截面为第20炮位置的单炮记录,右下截面为第50道炮检距位置的共炮检距剖面,深水造成的海底反射和由盐丘产生的长周期多次波具有陡峭的倾角.图 5b为去掉50%随机选取的地震道和所有5条近炮检距地震道后的数据,此时数据的缺失造成具有大倾角的反射波和多次波在远炮检距处出现空间假频,以往的seislet变换不能很好地表征有效信息,而改进的反假频seislet变换能够压缩存在假频的大倾角同相轴,结合Bregman迭代算法,能够恢复缺失的主要信息,此时迭代次数为20,在每次迭代中软阈值为固定值99%,该算法能够快速地进行地震数据插值,同时为了加快计算速度,还可以对所有炮记录进行并行计算,结果如图 5c所示.为了比较插值的效果,计算图 5a和图 5c的差异剖面(图 5d),从图中可以看到,由于近炮检距位置的数据恢复只能根据邻道数据进行预测,因此具有相对较大误差,但其它位置都显示较小的插值误差,可以证明本次研究的方法具有较好的结果.
|
图 5 实际地震数据 (a)实际炮集;(b)随机去掉50%数据的炮集;(c)插值结果;(d)差异剖面. Fig. 5 Real seismic data (a) Field shot gathers; (b) Shot gathers with 50% randomly selected traces removed; (c) Interpolated result; (d) Difference section between figure 4a and 4c. |
本文论述一种seislet变换的反假频形式,通过结合Bregman迭代方法来解决地震数据插值问题.将地震数据插值问题归纳为基追踪问题,利用Bregman迭代方法求解一系列非约束问题,以求取约束问题的解.当与seislet稀疏变换相结合时,该方法能够在满足一定插值误差要求的前提下进行有效的反假频地震数据重建.通过对理论模型和实际地震记录进行处理,验证了该迭代方法能够提供合理的插值结果.
6 附录A 小波变换提升算法提升方案是构造第二代小波变换的快速算法,不依赖Fourier变换,主要由简单的加减运算实现正反小波变换.通过改造预测算子和更新算子可以实现seislet变换.提升算法的步骤如下:
(1) 利用Sweldens(1995)[37]的方法将输入数据分成奇序列o和偶序列e.
(2) 计算奇序列与偶序列预测值之间的残差r,

|
(A1) |
其中,P是预测算子,可以利用Sweldens和Schröder(1996)[38]介绍的方法求取.
(3) 通过修正偶序列,计算数据的近似值c,
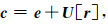
|
(A2) |
其中,U是更新算子,可以利用Sweldens和Schröder(1996)[38]介绍的方法求取.
(4) 近似值c成为新的数据,重复以上步骤得到下一级数的变换系数.
提升方案下的逆变换形式也可以很简单地定义,提升方案的反算子提供了反变换的运算法则.
(5) 将近似值c和近似级数下的残差r作为输入数据.
(6) 通过方程(A2)中的反向运算,重建偶序列成分e,
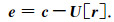
|
(A3) |
(7) 通过方程(A1)的反向运算,重建奇序列成分o,
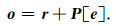
|
(A4) |
(8) 重组奇序列和偶序列成分,生成上一级数尺度的数据,重复上面步骤重建原始数据.离散小波变换结果由近似级数尺度下的近似数据和所有级数尺度下的残差组成,设计一种有效变换的关键在于确保预测算子P留下最小的残差而更新算子U保留原始数据中必要的特征并进入下一级数的运算.
致谢通讯作者感谢美国德州大学奥斯汀分校经济地质局SergeyFomel教授的建议和帮助.作者感谢两位匿名审稿人提出的宝贵意见,对提高本文质量起到了重要的作用.
| [1] | Gardner G H F, Canning A. Effects of irregular sampling on 3-D prestack migration. SEG Extended Abstract , 1994: 1553-1556. |
| [2] | Verschuur D J, Berkhout A J, Wapenaar C P A. Adaptive surface-related multiple elimination. Geophysics , 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [3] | Zhang Y, Zhang G Q, Bleistein N. True amplitude wave equation migration arising from true amplitude one-way wave equations. Inverse Problems , 2003, 19(5): 1113-1138. DOI:10.1088/0266-5611/19/5/307 |
| [4] | Morice S, Ronen S, Canter P, et al. The impact of positioning differences on 4D repeatability. SEG Extended Abstract , 2000: 1611-1614. |
| [5] | Mazzucchelli P, Rocca F. Regularizing land acquisitions using shot continuation operators:effects on amplitudes. SEG Extended Abstract , 1999: 1995-1998. |
| [6] | 辛可锋, 王华忠, 王成礼, 等. 叠前地震数据的规则化. 石油地球物理勘探 , 2002, 37(4): 311–317. Xin K F, Wang H Z, Wang C L, et al. Regularization of pre-stack seismic data. Oil Geophysical Prospecting (in Chinese) , 2002, 37(4): 311-317. |
| [7] | 管路平, 唐亚勋, 王华忠. 共偏移距道集平面波叠前时间偏移与反偏移. 地球物理学报 , 2009, 52(5): 1301–1309. Guan L P, Tang Y X, Wang H Z. Common-offset plane-wave prestack time migration and demigration. Chinese J. Geophys. (in Chinese) , 2009, 52(5): 1301-1309. |
| [8] | Claerbout J F. Earth Soundings Analysis:Processing Versus Inversion. Boston:Blackwell Scientific Publications, 1992. http://www.oalib.com/references/18986316 |
| [9] | 李信富, 李小凡. 分形插值地震数据重建方法研究. 地球物理学报 , 2008, 51(4): 1196–1201. Li X F, Li X F. Seismic data reconstruction with fractal interpolation. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1196-1201. |
| [10] | Wang Y B, Luo Y, Schuster G T. Interferometric interpolation of missing seismic data. Geophysics , 2009, 74(3): SI37-SI45. DOI:10.1190/1.3110072 |
| [11] | 高建军, 陈小宏, 李景叶, 等. 基于非均匀Fourier变换的地震数据重建方法研究. 地球物理学进展 , 2009, 24(5): 1741–1747. Gao J J, Chen X H, Li J Y, et al. Study on reconstruction of seismic data based on nonuniform Fourier transform. Progress in Geophys. (in Chinese) , 2009, 24(5): 1741-1747. |
| [12] | Xu S, Zhang Y, Pham D, et al. Antileakage Fourier transform for seismic data regularization. Geophysics , 2005, 70(4): V87-V95. DOI:10.1190/1.1993713 |
| [13] | 孟小红, 郭良辉, 张致付, 等. 基于非均匀快速傅里叶变换的最小二乘反演地震数据重建. 地球物理学报 , 2008, 51(1): 235–241. Meng X H, Guo L H, Zhang Z F, et al. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform. Chinese J. Geophys. (in Chinese) , 2008, 51(1): 235-241. |
| [14] | 张红梅, 刘洪. 基于稀疏离散τ-p变换的叠后地震道内插. 石油地球物理勘探 , 2006, 41(3): 281–285. Zhang H M, Liu H. Interpolation of poststack seismic traces based on sparse discrete τ-p transform. Oil Geophysical Prospecting (in Chinese) , 2006, 41(3): 281-285. |
| [15] | 王维红, 裴江云, 张剑锋. 加权抛物Radon变换叠前地震数据重建. 地球物理学报 , 2007, 50(3): 851–859. Wang W H, Pei J Y, Zhang J F. Prestack seismic data reconstruction using weighted parabolic Radon transform. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 851-859. |
| [16] | Candés E. Compressive sampling. Proceedings of International Congress of Mathematicians, 2006:1433-1452. http://www.oalib.com/references/16875837 |
| [17] | Donoho D L. Compressed sensing. IEEE Transactions on Information Theory , 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [18] | Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm. Geophysics , 2006, 71(6): E91-E97. DOI:10.1190/1.2356088 |
| [19] | Zwartjes P M, Sacchi M D. Fourier reconstruction of nonuniformly sampled, aliased seismic data. Geophysics , 2007, 72(1): V21-V32. DOI:10.1190/1.2399442 |
| [20] | 唐刚, 杨慧珠. 基于泊松碟采样的地震数据压缩重建. 地球物理学报 , 2010, 53(9): 2181–2188. Tang G, Yang H Z. Seismic data compression and reconstruction based on Poisson Disk sampling. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2181-2188. |
| [21] | 刘国昌, 陈小宏, 郭志峰, 等. 基于Curvelet变换的缺失地震数据插值方法. 石油地球物理勘探 , 2011, 46(2): 237–246. Liu G C, Chen X H, Guo Z F, et al. Missing seismic data rebuilding by interpolation based on Curvelet transform. Oil Geophysical Prospecting (in Chinese) , 2011, 46(2): 237-246. |
| [22] | 曹静杰, 王彦飞, 杨长春. 地震数据压缩重构的正则化与零范数稀疏最优化方法. 地球物理学报 , 2012, 55(2): 596–607. Cao J J, Wang Y F, Yang C C. Seismic data restoration based on compressive sensing using the regularization and zero-norm sparse optimization. Chinese J. Geophys. (in Chinese) , 2012, 55(2): 596-607. |
| [23] | Fomel S, Liu Y. Seislet transform and seislet frame. Geophysics , 2010, 75(3): V25-V38. DOI:10.1190/1.3380591 |
| [24] | 刘洋, FomelS, 刘财, 等. 高阶seislet变换及其在随机噪声消除中的应用. 地球物理学报 , 2009, 52(8): 2142–2151. Liu Y, Fomel S, Liu C, et al. High-order seislet transform and its application of random noise attenuation. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2142-2151. |
| [25] | Liu Y, Fomel S. OC-seislet:seislet transform construction with differential offset continuation. Geophysics , 2010, 75(6): WB235-WB245. DOI:10.1190/1.3479554 |
| [26] | Fomel S. Applications of plane-wave destruction filters. Geophysics , 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [27] | Tikhonov A N. Solution of incorrectly formulated problems and the regularization method. Soviet Mathematics-Doklady, 1963. |
| [28] | Fomel S. Shaping regularization in geophysical estimation problems. Geophysics , 2007, 72(2): R29-R36. DOI:10.1190/1.2433716 |
| [29] | Crawley S. Seismic trace interpolation with nonstationary prediction error filters. California:Stanford University, 2000. |
| [30] | Liu Y, Fomel S. Seismic data interpolation beyond aliasing using regularized nonstationary autoregression. Geophysics , 2011, 76(5): V69-V77. DOI:10.1190/geo2010-0231.1 |
| [31] | Fomel S. Three-dimensional seismic data regularization. California:Stanford University, 2001. http://www.oalib.com/references/18986305 |
| [32] | Gao J, Chen X H, Li J, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method. Applied Geophysics , 2010, 7(3): 229-238. DOI:10.1007/s11770-010-0246-5 |
| [33] | Osher S, Burger M, Goldfarb D, et al. An iterative regularization method for total variation-based image restoration. Multiscale Modeling & Simulation , 2005, 4(2): 460-489. |
| [34] | Yin W, Osher S, Goldfarb D, et al. Bregman iterative algorithms for L1 minimization with applications to compressed sensing. SIAM Journal on Imaging Sciences , 2008, 1(1): 143-168. DOI:10.1137/070703983 |
| [35] | Daubechies I, Defries M, de Mol C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics , 2004, 57(11): 1413-1457. DOI:10.1002/(ISSN)1097-0312 |
| [36] | Donoho D L. De-noising by soft-thresholding. IEEE Transactions on Information Theory , 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [37] | Sweldens W. Lifting scheme:A new philosophy in biorthogonal wavelet constructions. Wavelet Applications in Signal and Image Processing Ⅲ, Proceedings of SPIE 2569, 1995:68-79. http://www.oalib.com/references/17194330 |
| [38] | Sweldens W, Schroder P. Building your own wavelets at home, Wavelets in Computer Graphics. ACM SIGGRAPH Course notes , 1996: 15-87. |
 2013, Vol. 56
2013, Vol. 56


