近20年来,地震资料偏移处理能力得到了突飞猛进的发展.偏移技术由叠后发展到叠前、由时间域发展到深度域、由振幅相对保持发展到真振幅、由单程波发展到双程波等等.伴随着偏移技术的进步,各种成像技术也在不断涌现.叠后偏移技术对应的是零时刻成像条件[1];最早应用于叠前偏移的是互相关成像条件[2],即将延拓后的震源波场和检波点波场做互相关计算,这种成像条件效率高、计算稳定,但它只体现了地震波传播的运动学特征,亦即只包含相位信息的正确性、不具备保幅性.与真振幅对应的是地震波传播的动力学特征[3-6];基于炮域的保幅偏移采用的是反褶积成像条件,但是这种成像条件存在明显缺陷,即当分母项趋于零时计算不稳定.为了消除反褶积型成像条件中的不稳定因素,Valenciano等[7-10]对此做了一些有益的工作,总体思路是通过在分母中加入阻尼因子或对分母项平滑、以期消除奇异值.照明技术有助于偏移数据处理[11-13].Kirchhoff积分法叠前深度偏移成像中的照明技术研究比较成熟;波动方程叠前深度偏移成像中的照明技术也在发展之中,Wu等[12],Rickett[13]将地震观测系统中震源激发的地震波在地下传播过程中的能量分布作为地下照明的量度,用于进行偏移成像结果的振幅校正.一些学者[14-19]利用成像过程中存在的空间和时间两个方向上的变化规律,在角度域对成像过程进行了计算和分析,或者引入多参数约束成像条件,压制相关干扰,有效地改善了成像质量,为后续的速度分析奠定了基础.所有这些工作,均是建立在反褶积理论基础之上的;反褶积型成像方法是它们的基础.在实际地震资料的数据处理中,由于波动性及误差干扰等因素,即使在反射界面已知的情况下,反射波与入射波的比值仍然在较大的范围分布,这与传统理论中的射线理论出入较大.本文主要研究这些比值的分布规律及其可靠性值;显然,可以将其应用于角度域等具体的成像条件中,所得到的成像结果可以更加稳定、可靠.这些后续将在今后的工作中专门进行研究.
复杂介质中任何地震偏移计算都是近似的;地震波传播到地层深处,经过球面扩散及地层吸收作用之后,地震信号中的有用信息越来越弱,噪声部分越来越强.理论上讲,对于空间的某一固定点而言,作为输出的反射波与作为输入的入射波的比值应该在一个合理的范围之内.对于反褶积型成像条件而言,分子与分母分别对应的是检波点波场与震源波场.分母大于分子时,最后的成像数值比较小,对应的频率成分对偏移结果贡献不大;若某一频率成分对应的分母值接近于零而分子值又比较大时,输出远远大于输入,超出正常的合理性.由于偏移算法本身的局限性、照明不足或者该频率信号自身包含有较大误差等原因,导致计算结果严重影响其它频率成分、尤其是那些比值落在正常范围之内的频率成分对偏移成像的作用,甚至最终影响到整个偏移成像计算的可靠性.
本文以Marmousi模型的偏移成像结果作为评判标准,利用检波点能量与震源能量比值构造衰减系数,分析反褶积与自相关两类成像条件中各种频率成分检波点波场能量与震源波场能量两者比值的分布范围及不同分布范围对偏移成像的作用.构造衰减系数有利于克服反褶积型成像条件中分母趋于零时计算不稳定现象,也有利于平滑检波点波场与震源波场.检波点能量与震源能量比值超出正常范围容易导致偏移结果中出现照明不均匀现象.本文方法有助于改善反褶积型成像条件的偏移计算,有助于应用照明技术指导偏移成像结果的振幅校正.
2 计算与分析采用反褶积型成像条件做地震资料偏移处理时,作为输出的反射波与作为输入的入射波的比值分布在一个较大的范围之内.在某些情况下,如当震源波场存在照明不足、检波点波场照明正常时,这种比值通常较大,不利于准确成像.本文以Marmousi模型为分析对象,采用数值计算方法分析反褶积型成像条件中各种范围分布的比值对偏移结果的贡献及合理性,所得结论同样适用于互相关型成像条件.
为了便于共炮道集波场数据的偏移计算与分析,首先对震源波场和检波点波场的能量进行归一化处理,即将震源总能量与对应的检波点总能量调整到同一个水平;为了便于分析低反射率产生的反射波,适当放大检波点能量(本文将检波点能量放大1000倍).第i地震道第n频率成分对应的检波点和炮点能量分别记为ER(i,n)、ES(i,n),然后做如下的计算(其中ε相当于阻尼因子,目的是避免分母值为0;引入阻尼因子是为了得到更佳的偏移成像结果;可以采用模型计算的方法,首先对炮点数据能量进行归一化处理,然后,引入一组不同的阻尼因子进行计算,选择其中效果最好的作为最终的阻尼因子.此处采用双精度计算且取ε=10-33):
|
(1a) |

|
(1b) |
|
(1c) |
两种特例:(1)当检波点和震源能量相等,即Rsbr(i,n)=Rrbs(i,n)=1时,r(i,n)=1,ρ(i,n)=0;(2)当检波点和震源能量相差悬殊时,Rsbr(i,n)(或Rrbs(i,n))→+∞,r(i,n)→0,ρ(i,n)→-1.于是有-1≤ρ(i,n)≤0.因此,在反褶积型成像条件中,根据ρ(i,n)的值可以大致判断Rsbr(i,n)或Rrbs(i,n)的值.在[-1, 0]区间内,我们分5组进行计算与分析,分别为c=0.0、-0.25、-0.5、-0.75、-1.0.引入衰减系数:
|
(2) |
取衰减系数中的衰减因子分别为k=1/9、1/3、1、3、9、99,然后进行成像计算,公式如下:

|
(3) |
式中,UR(i,n)、US(i,n)分别代表检波点与震源延拓后的第n个频率对应的波场,N为波场频率总个数,*号表示共轭.
一般说来,对于某一个固定的ρ(i,n)值,既有Rsbr(i,n)≤Rrbs(i,n),也有Rsbr(i,n)≥Rrbs(i,n).根据反褶积型成像表达式,Rsbr(i,n)≥Rrbs(i,n)时波场数据对最后成像的贡献通常不大.因此,在这里仅分析Rsbr(i,n)≤Rrbs(i,n)这种情况.在上面的衰减系数表达式中,以k=99为例进行分析.对于同一个常数c而言,当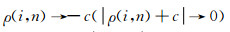
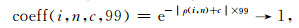
|
而当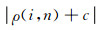
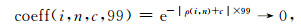
|
此时根据检波点与震源能量的差异,对ρ(i,n)值靠近-c的成像数值予以保留、远离-c的成像数值予以衰减,以便显示ρ(i,n)=-c及其附近区域对偏移成像结果的作用大小.依次可以分析其它5个衰减因子(见表 1),差别是它们对ρ(i,n)值远离-c的波场成分衰减程度不同而已.
|
|
表 1 coeff(i,n,c,99)中各种不同衰减因子对偏移成像的作用范围分析 Table 1 Analysis of the attenuation factors coeff(i, n, c, 99) upon the migration results |
分析两种特殊衰减因子:
(1)c=0.0所对应的情况
该衰减因子的作用结果是保留Rrbs(i,n)→ 1、衰减Rrbs(i,n)→+∞所对应的波场数据.从图 1(a-f)可知,k=1/9时衰减系数对Rrbs(i,n)→ +∞衰减作用不大;随后几组衰减因子对Rrbs(i,n)→ +∞部分数据的衰减作用逐步增大,成像效果后来变差,最后只剩下一些位于深部、界面起伏较缓的简单构造成像.这说明了两个问题:(1)Rrbs(i,n)→ + ∞部分数据对偏移成像的作用较大;(2)深层缓变构造对应的是Rrbs(i,n)→1.

|
图 1 c=0时各种衰减因子对应的反褶积型成像条件偏移结果 ((a-f)中的衰减因子分别为k=1/9、1/3、1、3、9、99) Fig. 1 Migration results of various attenuation factors with c=0 in deconvolutional imaging condition (The attenuation factors in (a-f) are k=1/9, 1/3, 1, 3, 9, 99 correspondingly) |
(2)c=1.0所对应的情况
该组数据主要是保留Rrbs(i,n)→+ ∞、衰减Rrbs(i,n)→1所对应的波场数据.从图 5(a-f)可知,k=1/9时衰减系数对Rrbs(i,n)→1衰减作用不大,成像效果比较好;随后几组衰减因子对Rrbs(i,n)→1部分数据的衰减作用逐步增大,成像效果变差,但主要构造在成像结果中依旧有所显示.这说明Rrbs(i,n)→+ ∞部分数据对成像的作用比较大.

|
图 5 c=1.0时各种衰减因子对应的反褶积型成像条件偏移结果,(a-f)中的衰减因子分别为k=1/9、1/3、1、3、9、99. Fig. 5 Migration results of various attenuation factors with c=1.0 in deconvolutional imaging condition (The attenuation factors in (a-f) are k=1/9, 1/3, 1, 3, 9, 99 correspondingly) |
另外,从图 1f、2f、3f、4f、5f可以看出,在各部分波场数据中,只有Rrbs(i,n)→+ ∞所对应的数据体对最终成像结果影响最大;参照图 1a、2a、3a、4a、5a及图 5f可以看出:图 5f中的偏移结果与Marmousi模型的照明效果非常吻合;偏移结果中出现的与照明有关的现象基本上都是由Rrbs(i,n)→+ ∞这部分数据体产生的.更进一步地,可以引入

|
图 2 c=0.25时各种衰减因子对应的反褶积型成像条件偏移结果 ((a-f)中的衰减因子分别为k=1/9、1/3、1、3、9、99) Fig. 2 Migration results of various attenuation factors with c=0.25 in deconvolutional imaging condition (The attenuation factors in (a-f) are k=1/9, 1/3, 1, 3, 9, 99 correspondingly) |

|
图 3 c=0.50时各种衰减因子对应的反褶积型成像条件偏移结果 ((a-f)中的衰减因子分别为k=1/9、1/3、1、3、9、99) Fig. 3 Migration results of various attenuation factors with c=0.50 in deconvolutional imaging condition (The attenuation factors in (a-f) are k=1/9, 1/3, 1, 3, 9, 99 correspondingly) |

|
图 4 c=0.75时各种衰减因子对应的反褶积型成像条件偏移结果 ((a-f)中的衰减因子分别为k=1/9、1/3、1、3、9、99) Fig. 4 Migration results of various attenuation factors with c=0.75 in deconvolutional imaging condition (The attenuation factors in (a-f) are k=1/9, 1/3, 1, 3, 9, 99 correspondingly) |
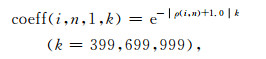
|
(4) |
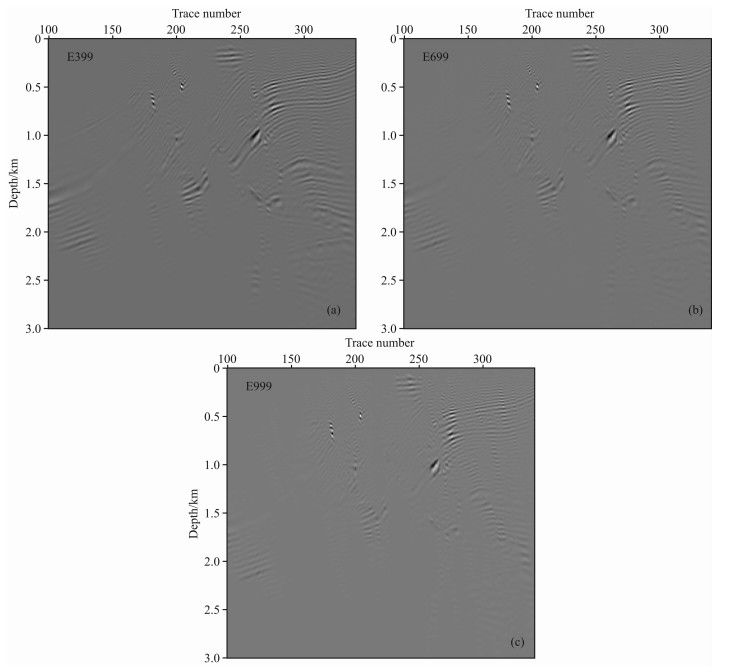
即衰减因子分别为k=399、699、999,对应的偏移结果分别显示在图 6(a-c)中,从图 6不难看出偏移结果与衰减系数、衰减因子之间的关系.因此,可以依据衰减系数设计照明量度指导波动方程进行照明技术分析与数值计算.
|
图 6 c=1.0时各种衰减因子对应的反褶积型成像条件偏移结果 ((a-c)中的衰减因子分别为k=399、699、999) Fig. 6 Migration results of various attenuation factors with c=1.0 in deconvolutional imaging condition (The attenuation factors in (a-c) are k=399, 699, 999 correspondingly) |
对互相关型成像条件进行类似的计算与分析,可以得到类似的结论.
3 结论成像条件对地震资料偏移处理至关重要.反褶积型成像条件的计算不稳定及分析这种不稳定根源,有助于改善偏移质量.
本文利用检波点与震源能量比值进行计算与分析.在构造不太复杂地区,这种比值分布在一定范围之内.对于浅层水平或近似水平层状介质,成像效果高,检波点与震源能量的比值分布范围相对大一些;对于上覆地层简单的深部水平或近似水平构造,检波点与震源能量的比值分布范围相对小一些.在复杂构造地区,这种比值分布范围较大,较大比值部分对偏移结果作用较大,容易引起偏移结果中的照明不均匀等现象.
本文方法可以用于克服反褶积型成像条件中分母趋于零时计算不稳定现象及平滑检波点波场与震源波场,有助于分析偏移结果中出现的照明不均匀现象,也有助于应用照明技术指导偏移成像结果的振幅校正.
| [1] | Schultz P S, Sherwood J W C. Depth migration before stack. Geophysics , 1980, 45(3): 376-393. DOI:10.1190/1.1441088 |
| [2] | Claerbout J F. Imaging the earth's interior. Cambridge, MA: Blackwell Scientific Publications, 1985. |
| [3] | 孙建国. Kirchhoff型真振幅偏移与反偏移. 勘探地球物理进展 , 2002, 25(6): 1–5. Sun J G. Kirchhoff-type true-amplitude migration and demigration. Progress in Exploration Geophysics (in Chinese) , 2002, 25(6): 1-5. |
| [4] | 张关泉. 波动方程的上行波和下行波的耦合方程组. 应用数学学报 , 1993, 16(2): 251–263. Zhang G Q. System of coupled equations for up-coming and down-going waves. Acta Math. Appl. Sinica (in Chinese) , 1993, 16(2): 251-263. |
| [5] | 张关泉.波场分裂、平方根算子与偏移. //反射地震学论文集.上海:同济大学出版社, 2000: 16-20. Zhang G Q. Wavefield splitting, square root operator and migration. // Collected papers on the reflection seismology (in Chinese). Shanghai: Tongji University Press, 2000: 16-20. http://www.oalib.com/references/18986242 |
| [6] | 张宇. 振幅保真的单程波方程偏移理论. 地球物理学报 , 2006, 49(5): 1410–1430. Zhang Y. The theory of true amplitude one-way wave equation migration. Chinese J. Geophys (in Chinese) , 2006, 49(5): 1410-1430. |
| [7] | Valenciano A, Biondi B. 2D deconvolution imaging condition for shot profile migration. Expanded Abstracts of 73rd SEG Meeting, 2003, 1059-1062. |
| [8] | Guitton A, Valenciano A, Bevc D, et al. Smoothing imaging condition for shot profile migration. Geophysics , 2007, 72(3): S149-S154. DOI:10.1190/1.2712113 |
| [9] | Schleicher J. A comparison of imaging conditions for wave-equation shot-profile migration. Expanded Abstracts of 77th SEG Meeting, 2007, 2393-2397. http://www.oalib.com/references/18986246 |
| [10] | Antoine G, Valenciano A. Robust imaging condition for shot-profile migration. Expanded Abstracts of 76PthP SEG Meeting, 2006, 2519-2522. http://www.oalib.com/paper/4868374 |
| [11] | Kaelin B, Guitton A. Imaging condition for reverse time migration. Expanded Abstracts of 76th SEG Meeting, 2006, 2594-2597. http://www.oalib.com/references/18991963 |
| [12] | Wu R S, Chen L. Mapping directional illumination and acquisition-aperture efficacy by beamlet propagators. Expanded Abstracts of 72nd SEG Meeting, 2002, 1352-1355. http://www.oalib.com/references/18986248 |
| [13] | Rickett J E. Illumination-based normalization for wave-equation depth migration. Geophysics , 2003, 68(4): 1371-1379. DOI:10.1190/1.1598130 |
| [14] | Xie X B, Wu R S. Extracting angle domain information from migrated wavefield. Expanded Abstracts of 72nd SEG Meeting, 2002, 1360-1363. http://www.oalib.com/references/18986622 |
| [15] | Sava P, Biondi B. Wave equation migration velocity analysis. I. Theory. Geophysical Prospecting , 2004, 52(6): 593-606. DOI:10.1111/gpr.2004.52.issue-6 |
| [16] | Soubaras R. Angle gathers for shot-record migration by local harmonic decomposition. Expanded Abstracts of 73rd SEG Meeting, 2003, 889-892. http://www.oalib.com/references/18991023 |
| [17] | Sava P C, Fomel S. Angle-domain common-image gathers by wavefield continuation methods. Geophysics , 2003, 68(3): 1065-1074. DOI:10.1190/1.1581078 |
| [18] | Rickett J E, Sava P C. Offset and angle-domain common image-point gathers for shot-profile migration. Geophysics , 2002, 67(3): 883-889. DOI:10.1190/1.1484531 |
| [19] | Ng M. Using time-shift imaging condition for seismic migration interpolation. Expanded Abstracts of 77th SEG Meeting, 2007, 2378-2382. http://www.oalib.com/references/18986254 |
 2013, Vol. 56
2013, Vol. 56