2. 吉林大学物理学院, 长春 130023;
3. 塔里木油田公司勘探开发研究院, 新疆库尔勒 841000
2. Physics College, Jilin University, Changchun 130023, China;
3. Research Institute of Petroleum Exploration and Development of Tarim Oil Field, Xinjiang 841000, China
阵列感应测井是一种很重要的电测井方法,它具有测量信息大、分辨率高、探测深度深、反映侵入直观等优点,已广泛应用于国内外的油田测井中.但在应用中阵列感应测井也暴露出一些资料质量问题,如其浅探测曲线经常出现异常跳变、各探测深度曲线乱序等.导致浅探测曲线出现异常的原因有目的层电阻率与围岩电阻率反差较大[1-2]、盐水泥浆条件下的井眼不光滑[3-4]、大斜度井眼或倾斜地层[5]、仪器偏心[6]等.在阵列感应测井的数据处理中井眼是看做圆形处理的,在作井眼校正时只考虑井眼斜度、泥浆、仪器偏心及扩径或缩径对测量响应的影响[7-8].事实上,在钻井过程中,由于受应力作用,井眼受到挤压或井壁垮塌,井眼形状不是圆形的,通常呈椭圆或拟椭圆形的.这种圆形井眼的假设对实际阵列感应测井的影响有多大尚未见公开的文章发表.另外,虽然阵列感应测井在作数据处理[9]时要做仪器偏心校正和井斜校正,但偏心和井斜对各阵列曲线影响的程度有多大、这种校正是否完善、在现场测井或资料解释时需要注意什么等需要进一步进行考察和验证.本文使用三维矢量有限元方法考察井眼环境对国内应用较多的5700系统高分辨率阵列感应测井(HDIL)响应的影响,由于泥浆矿化度以及井径大小的适用范围在阵列感应测井仪器指标里已有说明且其影响基本上是单向的,这里只考虑井眼形状、仪器偏心和井斜对阵列感应测井的影响[10-11].
HDIL仪器共有7个基本阵列单元,每个基本阵列单元都采用8种工作频率(10、30、50、70、90、110、130和150kHz),共测量112个信号(包括实部和虚部),这里只考虑56个实部信号.经数据处理后得到3种垂向分辨率[1ft(0.3m)、2ft(0.6m)和4ft(1.2m)]、6种探测深度[10in(0.25m)、20in(0.51m)、30in(0.76 m)、60in(1.52 m)、90in(2.29 m)和120in(3.05m)]共18条测井曲线.HDIL仪器在标准井眼条件下(井径为20cm)井下的可探测范围为(0.6m系列):泥浆电阻率(地层条件下)大于0.02Ωm、地层电阻率与泥浆电阻率之比小于500、地层电阻率为0.2~200Ωm.文章计算所用的地层模型均在HDIL仪器可探测范围之内.
2 三维矢量有限元方法原理三维矢量有限元是一种计算三维空间条件下矢量场分布的方法.引入矢量元可满足交界面上切向场的连续性,同时可对旋度算子的零空间进行准确的描述,从而解决采用结点元会产生伪解的问题.在不同井眼形状条件下阵列感应测量响应的计算可归结为三维坐标下电磁场矢势的求解.
2.1 三维矢量有限元计算格式由麦克斯韦方程可推得在地层介质中的场满足波动方程[12-15]
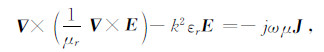
|
(1) |
式中μr为相对磁导率;μ为磁导率;ε为相对介电常数[16-17];E为电场强度;ω为圆频率;k为地层中电磁波波数;J为体电流密度.
在导体边界上要满足切向电场为0的条件,即第一类边界条件
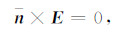
|
(2) |
由(1)式,三维空间中电磁场的计算等价于求下列泛函的极小值:
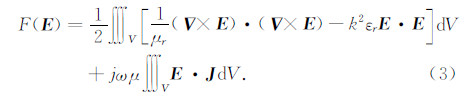
|
(3) |
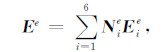
|
(4) |
式中Ee表示单元e内的矢量场;Eie为单元内第i个棱边的切向场分量;Nie为矢量插值函数或基函数.
将求解区域按四面体单元进行空间离散化(见图 1),则单元内矢量场可表示为
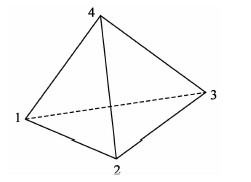
|
图 1 矢量四面体单元 Fig. 1 Vector unit of tetrahedron |
将(4)式代入(3)式,求解泛函(3)式在(2)式条件下的驻点,并使用全局编号,可得到线性方程组
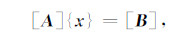
|
(5) |
式中为[A]系数矩阵,[B]为右端向量,{x}为待求场分布.(5)式为一超大型稀疏复对称形方程组,由于是三维空间,其条件数很大.本文采用Krylov子空间预处理双共轭梯度法(BICG)进行求解[18-22].
2.2 矩阵方程的求解
常用的方程组求解算法主要有共轭梯度法(CG)、双共轭梯度法(BCG)等,双共轭梯度法的求解速度要比共轭梯度法快得多,它是一种针对复数对称方程组的求解技术,公式推导是基于内积形式: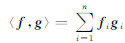
预处理技术是在求解有限元方程组之前通过对原有限元方程组的系数矩阵性态进行改善,从而可加快BICG的收敛速度,提高迭代稳定性.矩阵分裂技术是一种非常好的预处理方法.
基于矩阵分裂的预处理思想可一般描述为:假设矩阵[A]有分裂
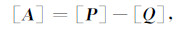
|
那么可以通过矩阵[P],[Q]来构造预处理矩阵[M].注意到预处理矩阵[M]自身就是[A]的近似,于是[A]可表示为

|
(6) |
这样[M]就称为[A]的分裂矩阵,而[Q]为误差矩阵.[M]的构造方法很多,比如Jacobi分裂([M]=diag([A]),Gauss-Seidel分裂([M]=diag([A]-[L]),[L]是[A]的严格下三角部分),SSOR分裂法等.下面我们仅以SSOR分裂为例来介绍预处理BICG法.
设对(5)式事先进行预处理,使得处理后的系数阵对角元值为1且仍对称.例如,假设
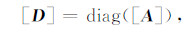
|
那么方程
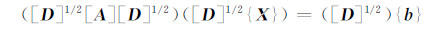
|
与方程(5)是等价的,于是令

|
(7) |
则方程(5)就转化为
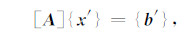
|
(8) |
而且[A]的对角元值为1,不失一般性,假设
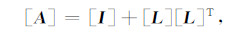
|
式中[L]是[A]的严格下三角部分.这时可取预处理矩阵为
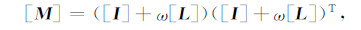
|
式中ω是权,称为预处理因子,用于控制收敛性,一般在0~2之间.
用[M]-1作用在(8)式的两端,有
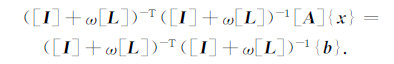
|
进一步变换可得
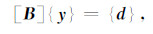
|
(9) |
这里
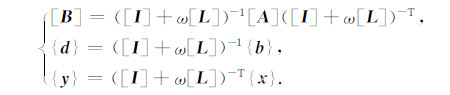
|
经过以上变换后,应用BICG法求解(9)式,得到{y}后再由(7)式进行一次回代过程就得到所求问题的解.由于矩阵[B]的性态比矩阵[A]的性态要好的多,因而应用BICG方法进行求解,速度将提高许多.
下面是三维矢量有限元方法在阵列感应影响因素考察中的具体应用.
3 井眼形状对阵列感应测井(HDIL)响应的影响在钻井过程中,由于受应力作用,井眼受到挤压或井壁垮塌,通常呈椭圆或拟椭圆形的.但在阵列感应测井数据处理过程中,井眼一般是按圆形来处理的,即使双井径仪探测出井眼形状相比钻头尺寸有较大变化,也是按大井眼(扩径)或小井眼(缩径)或井径均值来处理的.下面将井眼按椭圆形和圆形分别计算阵列感应的测量响应以考察按圆形井眼方式处理的影响大小.
3.1 椭圆井眼模型如图 2,其中左图为标准井眼,井眼形状为圆形,设井眼半径rH,仪器居井眼中心.右图为椭圆井眼,设a为椭圆井眼的长半轴,b为椭圆井眼的短半轴,椭圆度kEllip=a/b.图中rTool和rHole分别表示仪器半径和井眼半径.设标准井眼rH=0.1m,泥浆电阻率Rm=0.1Ωm,地层电阻率Rt=2.0;20.0;40.0Ωm,则Rt/Rm=20;200;400.每种地层HDIL7组线圈测量8种频率共112个信号,其中实部56种测量响应,这里不考虑虚部信号.
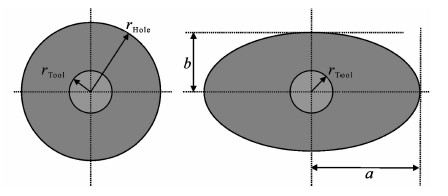
|
图 2 井眼模型 Fig. 2 Models of borehole |
设椭圆度影响系数为cof,先考虑对原始测量响应的影响.
定义cof=Mi/M0,
式中Mi为给定椭圆度测量响应,它是Rt、Rm、线圈距、频率及椭圆度的函数;M0为标准井眼的测量响应,它是Rt、Rm、线圈距及频率函数,椭圆度等于1.
当井眼为圆形时,椭圆度影响系数为1.0,大于或小于1.0均表示仪器受井眼形状的影响.
3.2 HDIL原始测量响应受井眼形状的影响考察图 3反映了不同测量线圈的原始测量响应在不同椭圆度条件下与圆形井眼相比下所受影响大小即椭圆度影响系数的大小.其中图 3a的Rt/Rm=20,线圈工作频率为150kHz,短半轴长0.1m.图的横坐标为椭圆度kEllip,纵坐标为椭圆度影响系数cof,图例中的A0~A6分别表示HDIL线圈距由小到大的7个线圈,以下各图符号意义均与此同.从图中看,线圈距越短,测量信号受椭圆度大小的影响越大,线圈距越长,测量信号几乎不受影响.当椭圆度较小时,各线圈测量信号受影响较小.
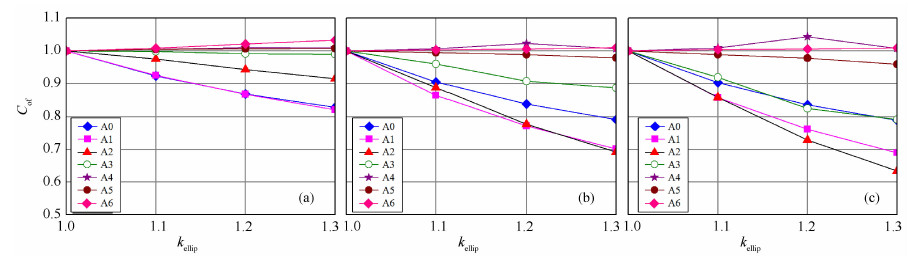
|
图 3 不同测量线圈测量响应受椭圆度的影响 Fig. 3 The effects of ellipticities on raw measurements of various coils |
图 3b的Rt/Rm=200,图 3c的Rt/Rm=400,其它条件均与图 3a相同.从这两个图中看,线圈距越短,测量信号受椭圆度大小的影响进一步加大,线圈距越长,测量信号受影响较小.
对比这3个图可以发现,当椭圆度一定时,Rt/Rm越大,各线圈测量信号所受影响也越大.
由于相比井眼形状,线圈工作频率对椭圆度影响系数的影响相对较小,为简化起见这里只考虑f=150kHz时井眼形状的影响,但在进行井眼校正及合成聚焦等数据处理时需要使用全部工作频率的测量信号.
3.3 HDIL合成聚焦曲线受井眼形状的影响考察下面考察对合成聚焦后的曲线的影响大小.对原始112个信号经过合成聚焦后可得到3种分辨率6种探测深度的曲线,设地层为无限厚,不同分辨率同种探测深度的曲线值是一样的,这里只考虑0.6m分辨率的阵列测井曲线.
定义相对误差rr为

|
(10) |
式中Vi为给定椭圆度测井值,它是Rt、Rm、频率、探测深度及椭圆度的函数;Vs为给定地层真电阻率.
图 4是0.6 m分辨率不同探测深度曲线受椭圆度的影响大小图,图例中M2R1、M2R2、M2R3、M2R6、M2R9、M2RX由浅至深分别对应6种不同的探测深度.图 4a、4b、4c的Rt/Rm分别为20、200、400.从图 4a看,各曲线在不同椭圆度下误差比较稳定,只是探测深度较深的曲线,相对误差相对较大,这可能与长距线圈在地层电阻率较低时受趋肤效应影响较大有关.

|
图 4 不同探测深度曲线受椭圆度的影响大小 Fig. 4 The effects of ellipticities on logs of HDIL |
从图 4b看,探测深度较深的曲线表现较为稳定,而探测深度较浅的曲线受较大的椭圆度影响较大.
从图 4c看,除3.05 m曲线较为稳定外,其它曲线均不同程度地受椭圆度的影响,相对来说,0.25 m曲线受井眼环境影响最大.在实际测井曲线中,0.25 m的曲线也最不稳定.
比较图 4中3个图可以发现,当椭圆度一定时,Rt/Rm越大,各探测深度曲线受的影响也越大.因此在实际测井中,建议合理使用双井径曲线判断井眼形状对阵列感应测井响应的影响程度.
在不同地层模型和泥浆条件下,通过计算不同椭圆度下各探测深度曲线所受的影响大小可以建立不同椭圆度下的井眼形状校正图版.从图 4的3个图可以看出,这种校正是很有必要的.
在现场测井中,有时在测阵列感应时没有测井径曲线,而井径曲线在进行环境校正和合成聚焦时又要用到,于是有时现场快速处理时就用其它组合时的井径曲线,而其它组合时的井径曲线往往与在测阵列感应时的井径有不同.那么,用其它组合时的井径曲线对阵列感应测井响应的影响有多大即与实际的地层电阻率值相差有多大呢?图 5显示了这种处理的误差大小.该图Rt/Rm=400,椭圆度取1.3.图的纵坐标是相对误差,这里在式(10)中Vs取40,横坐标是各探测深度曲线,柱状图不同的颜色表示使用了不同的井径曲线,蓝色的表示用短轴作井径,褐色的表示用长轴作井径.
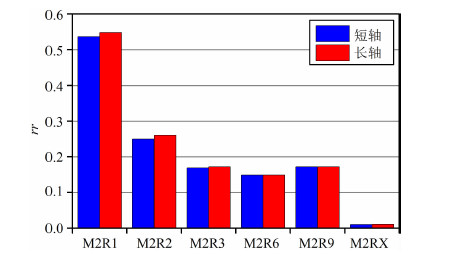
|
图 5 不同的井径对阵列感应各测井曲线的影响 Fig. 5 Comparison of true spectra and those calculated using two parameter vectors with different |
从图中看,浅探测曲线受井眼影响更大些,但无论是用短轴还是用长轴作井径,其相对误差变化不大.因此,在出现椭圆井眼的情况下处理HDIL数据,使用长轴或短轴井径数值相对误差变化不大,在数据处理时可以选用其它测井系列的井径曲线.
4 偏心对HDIL测井响应的影响 4.1 偏心地层模型如图 6,仪器偏心是指测量时,仪器中心偏离井轴中心一定距离,称为仪器偏心距.仪器最大偏心距=井眼半径-仪器半径.
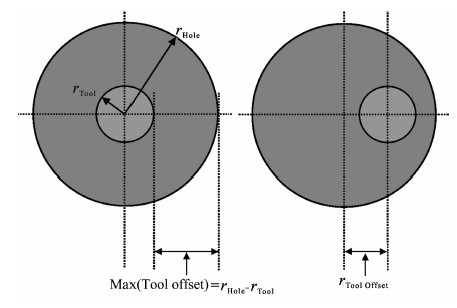
|
图 6 仪器偏心模型 Fig. 6 Models of tool eccentricity |
设标准井眼rH=0.1m,仪器半径rTool=0.05m,泥浆电阻率Rm=0.1Ωm,地层电阻率Rt=2.0、20. 0、40.0Ωm,则Rt/Rm=20、200、400.设仪器偏心距为Off(单位:m),仪器偏心影响系数为coo.当仪器居中时,偏心影响系数为1.0,大于或小于1.0均表示仪器受偏心影响.
定义coo=Mi/M0.
式中Mi为给定仪器偏心距测量响应,它是Rt、Rm、线圈距、频率及偏心距的函数;M0为仪器居中的测量响应,它是Rt、Rm、线圈距及频率函数,偏心距等于0.
4.2 在标准井眼条件下,仪器偏心程度对HDIL原始测量响应影响的考察图 7反映了不同测量线圈的原始测量响应在不同偏心距条件下与仪器居中相比下所受影响大小即仪器偏心影响系数的大小.其中图 7a,Rt/Rm=20,图 7b的Rt/Rm=200,图 7c的Rt/Rm=400,线圈工作频率为10kHz.图的横坐标为仪器偏心距Off,纵坐标为仪器偏心影响系数Coo.从图 7a看,线圈距越短,测量信号受仪器偏心大小的影响越大,线圈距越长,测量信号几乎不受影响.当仪器偏心较小时,各线圈测量信号受影响较小.
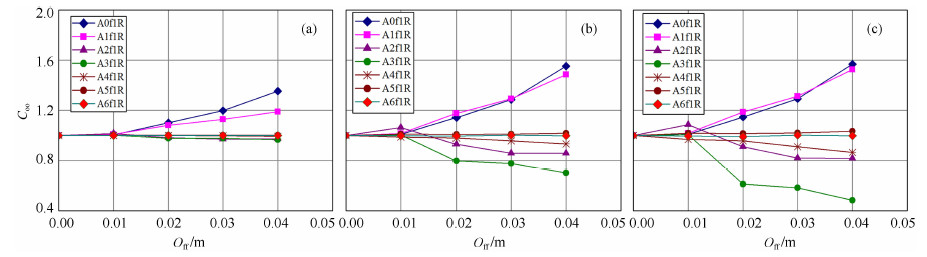
|
图 7 不同线圈测量响应受仪器偏心的影响大小 Fig. 7 The effects of tool eccentricity on raw measurements of various coils |
从图 7b与图 7c看,线圈距越短,测量信号受仪器偏心大小的影响进一步加大,线圈距越长,测量信号受仪器偏心影响较小.
对比图 7中的3张图可以发现,当仪器偏心距一定时,Rt/Rm越大,各线圈测量信号所受影响也越大.
4.3 在标准井眼条件下,仪器偏心程度对HDIL合成聚焦曲线影响的考察与式(10)类似,定义偏心相对误差rr为
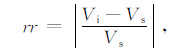
|
(11) |
式中Vi为给定偏心距测井值,它是Rt、Rm、频率、探测深度及仪器偏心距的函数;Vs为给定地层真电阻率.
图 8是井眼rH=0.15m,仪器半径rTool=0.05m时0.6 m分辨率不同探测深度曲线受仪器偏心的影响大小图,图例分别表示6种不同的探测深度.其中图 8a中,Rt/Rm=20,图 8b的Rt/Rm=200,图 8c的Rt/Rm=400.从图 8a看,在Rt/Rm较低时,各曲线在不同仪器偏心距下误差比较小,线圈距越短,偏心相对误差越大.图 8b中,Rt/Rm较大,各曲线在不同仪器偏心距下偏心相对误差变大,同样线圈距越短,偏心相对误差越大.但3.05 m探测深度曲线的相对误差较大,这与仪器线圈结构及合成聚焦算法有关.图 8c中,在Rt/Rm最大,各曲线在不同仪器偏心距下误差进一步变大,同样地,线圈距越短,偏心相对误差越大.
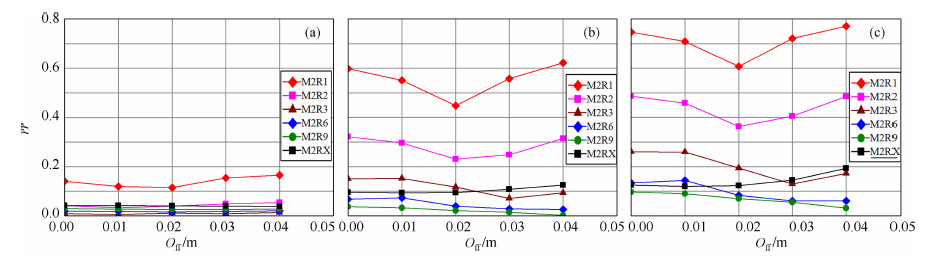
|
图 8 不同探测深度曲线受仪器偏心的影响大小 Fig. 8 True and inverted electrcc parameters of the wedge model |
比较图 8中3张图可以发现,当仪器偏心距一定时,Rt/Rm越大,各探测深度曲线基本上所受影响也越大,而浅探测曲线更易受仪器偏心的影响.因此在实际测井中,建议使用扶正器以减少仪器偏心对阵列感应测井响应的影响.但要注意不能让仪器贴靠井壁,仪器贴靠井壁会引起电磁场的突变而使测井信号产生异常.
图 9是井半径为0.15 m,Rt/Rm=400时各探测深度曲线在不同仪器偏心距下的相对误差统计图.图的纵坐标是相对误差,这里在式(11)中Vs取40Ωm,横坐标是各探测深度曲线,柱状图不同的颜色表示了两种不同的偏心距,蓝色的表示仪器居中,褐色的表示仪器偏心距为0.04m.
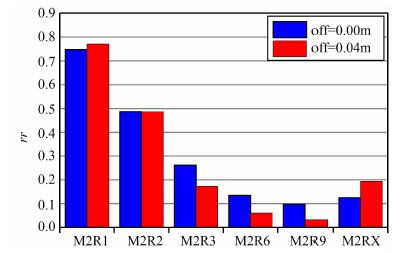
|
图 9 不同探测深度曲线在不同仪器偏心距下相对误差统计图(Rt/Rm=400) Fig. 9 The statistical chart of relative errors for array logs in different tool offsets |
从统计图上看,仪器居中和偏心4c m时相对误差变化不大,即仪器偏心程度对深浅探测曲线影响不大.浅探测曲线相对误差较大主要是受泥浆与地层电阻率间的反差影响.另外,3.05 m曲线的相对误差大于2.29 m曲线,因此在出现大井眼情况下,建议使用2.29 m曲线作为地层电阻率计算含油饱和度.
5 不同斜度井眼对HDIL测井响应的影响 5.1 考察模型仪器半径rTool=0.05m,井眼半径rHole=0.1m,泥浆电阻率Rm=0.5Ωm,地层厚度H=2.0m,目的层电阻率Rt=20.0Ωm,围岩电阻率Rs=3.0Ωm,如图 10,两道红斜线表示井眼.
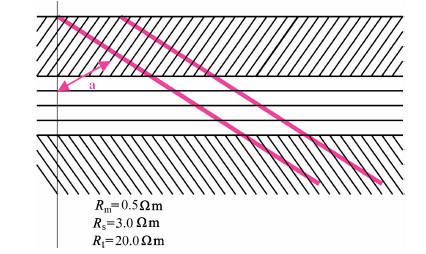
|
图 10 斜井地层模型图 Fig. 10 Formation model with slant borehole |
不同斜度的井眼与水平地层模型可以看做为直井和倾斜的地层模型,为此可令地层倾角分别为15、30、45、60、75和80°代表井眼斜度α为15、30、45、60、75和80°(井眼斜度为井眼轴与垂直方向的夹角).
5.2 考察结果与分析图 11是不同地层倾角下经模拟仪器响应后再合成聚焦出的阵列测井曲线计算结果,其中(a-f)子图的地层倾角分别是为15°、30°、45°、60°、75°、80°.每个图的第1道的两条曲线分别是井径曲线(CAL)和泥浆电阻率曲线(WRM),第2道为深度道,第3、4、5道分别为0.3m、0.6m、1.2 m分辨率6种探测深度的阵列测井曲线(图例中的第一个数字表示第几种分辨率,第二个数字表示第几种探测深度,如M1R1表示0.3 m分辨率0.25 m探测深度曲线、M4RX表示1.2 m分辨率3.05 m探测深度曲线).从图 11a上看,阵列测井曲线显示的地层厚度、围岩电阻率、目的层电阻率几乎与设计模型一致,说明15°的斜井或倾角为15°的地层条件下的测量结果与直井水平地层模型条件下的测量结果差别不大.1.2 m分辨率阵列测井曲线由于分辨率较低而不能较好地显示目的层厚度.图 11b阵列测井曲线显示的围岩电阻率、目的层电阻率几乎与设计模型一致,但地层厚度略有增加.与直井水平地层模型条件相比,30°的斜井或倾角为30°的地层条件下的计算结果差别也不大.
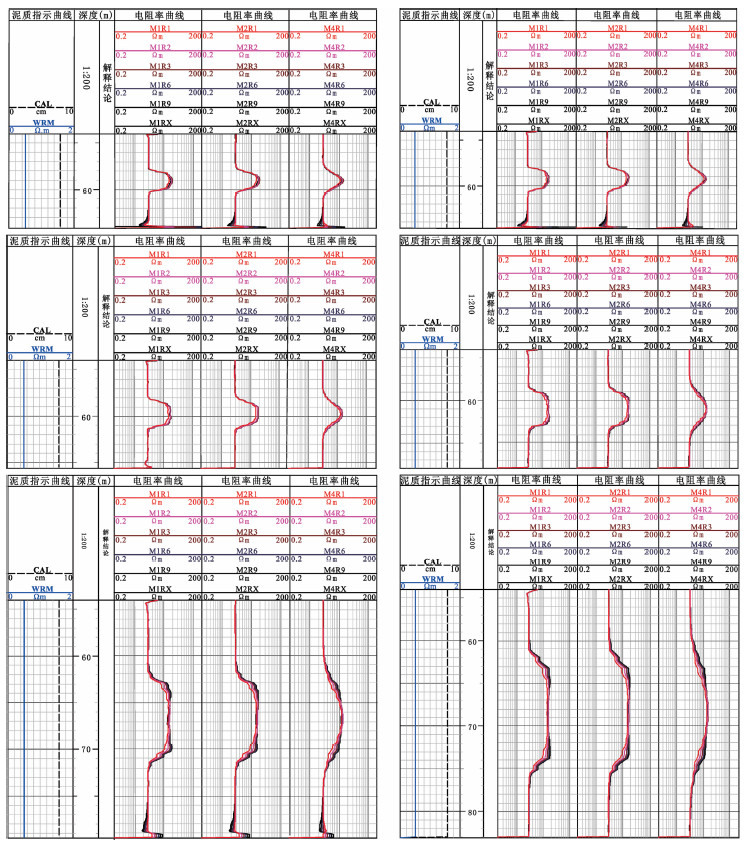
|
图 11 不同倾角地层条件下的计算结果 Fig. 11 The calculating results in formations with various dips |
图 11c的目的层电阻率比真电阻率有所减小,地层厚度也变宽.说明45°的斜井或倾角为45°的地层对测井结果有一定影响,需要进行一定校正处理. 图 11d的目的层电阻率比真电阻率有所减小,地层厚度进一步变宽.说明60°的斜井或倾角为60°的地层对测井结果影响在加大,需要进行进一步校正处理.图 11e的目的层电阻率比真电阻率有所减小,地层厚度变宽许多,地层界面附近有犄角和伪侵入现象出现,说明75°的斜井或倾角为75°的地层对测井结果影响在进一步加大,需要进行校正处理.图 11f目的层电阻率比真电阻率有所减小,地层厚度变宽很多,地层界面附近有犄角和伪侵入现象出现.80°的斜井或倾角为80°的测井结果已不能反映地层的真实情况,在实际解释处理中需要考虑这种影响.
总的说来,斜井或倾斜地层对阵列感应测井结果的影响表现在两个方面:一是地层视厚度,二是测量地层视电阻率.当井斜≤30°对视厚度基本没有影响,当井斜在30°~60°之间影响增大,井斜≥60°时不反映实际层厚.对测量地层视电阻率的影响可参见图 12a-12c,其横坐标为井斜角,纵坐标是与地层真电阻率相比的相对误差.这3张图分别显示了不同井斜角对0.3 m、0.6 m、1.2 m阵列感应测井视电阻率的影响大小.从这些图来看,对0.3 m和0.6 m阵列曲线,0.25 m探测曲线相对误差尽管较大,但其变化不大,即井眼斜度对0.25 m探测曲线几乎没有影响,其他探测曲线在60°以内影响不大,60°以上相对误差急剧增大,75°以后相对误差有所下降,使用时必须加以考虑;而对1.2 m阵列曲线,不同的井斜角下相对误差变化不大,即它们受井斜影响相对较小,但与0.3 m和0.6 m相比,其相对误差较大,这与其分辨率相对较低有关.
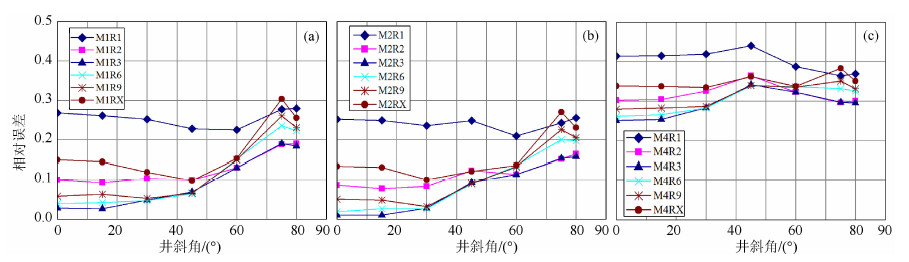
|
图 12 不同井斜角对不同分辨率阵列感应测井视电阻率的影响 Fig. 12 The effects of different deviation angles on HDIL logs with various vertical resolutions |
图 13是冀东油田一口井的HDIL实测曲线图,该井在图中深度段内的泥浆电阻率约为0.12Ωm.图中第一道是双井径曲线(CAL13和CAL24)和伽马曲线(GR);第二道是HDIL合成聚焦后的0.6m阵列曲线;第三道是HDIL经转换后的原始测量曲线(单位:mS/m),这里只选取了一种工作频率下7个阵列单元(图中从上至下线圈距由短至长排列)的测量结果(曲线名的第1个数字表示第几个阵列单元,第2个数字表示第几种工作频率);第五道是孔隙度曲线:声波时差(AC)、密度(DEN)以及补偿中子(CNL).从图上看,由深度2427.0 m至2432.6m,井眼椭圆度由约1.0逐渐增大至1.3,从2432.6 m以下井眼椭圆度又逐渐减小.由2432.0 m至2439.4 m属于泥岩段,其电阻率约为2.0Ωm,虽然岩性粗细有变化,但没有泥浆滤液侵入地层.Rt/Rm约为20,这与图 3a和图 4a的模型类似.从第三道的原始测量曲线看,长距线圈测量值变化较小,而短距线圈变化较快,虽然带有岩性变化的影响,但总的变化规律与图 3a相符.第二道中,如果取地层真电阻率约为2.0Ωm,则合成聚焦后的曲线总的变化规律与图 4a吻合.至于Rt/Rm更大的情形如200,一般为含油的储层段,由于储层段常常伴随着泥浆滤液的侵入,故它们受井眼椭圆度的影响大小不易分析.
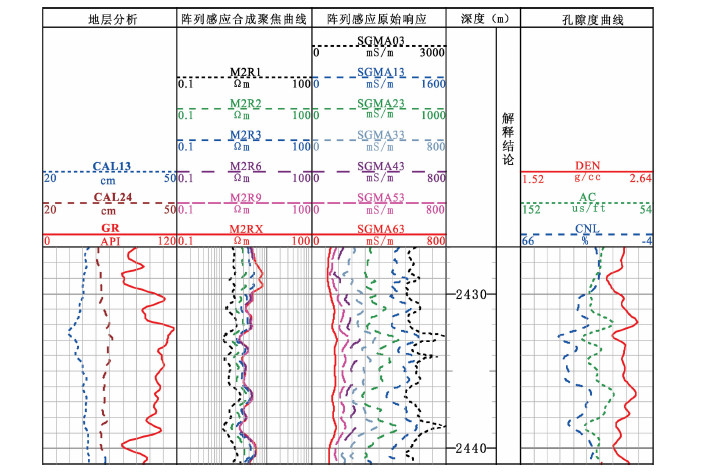
|
图 13 冀东油田XX井HDIL测井成果图 Fig. 13 The result of HDIL logs for Jidong oilfield XX well |
图 14是塔里木油田某口井的HDIL实测曲线图,图中第一道是井径(CAL)、自然伽马(GR)以及井斜(DEVI)曲线;第二、三、四道分别是HDIL合成聚焦后的0.3、0.6、1.2m阵列曲线.从图上看,在4930.0 m至4945.0 m深度段,井斜角大约是30°左右,第二、三道的0.3、0.6 m阵列曲线与第一道的自然伽马曲线无论是在砂岩层还是泥岩层均对应得很好;但在5060.0 m至5090.0 m深度段,井斜角大约是60°左右,与第一道的自然伽马曲线对比(自然伽马曲线也在一定程度上受井斜影响),第二、三道的0.3、0.6 m阵列曲线在砂岩层或泥岩层均被拉长,0.25 m曲线质量明显下降,同时在5074.0m至5088.0 m的非储层段,第二、三、四道的0.3、0.6、1.2 m阵列曲线出现假侵入现象,这些现象与图 11和图 12给出的模拟结果相吻合.
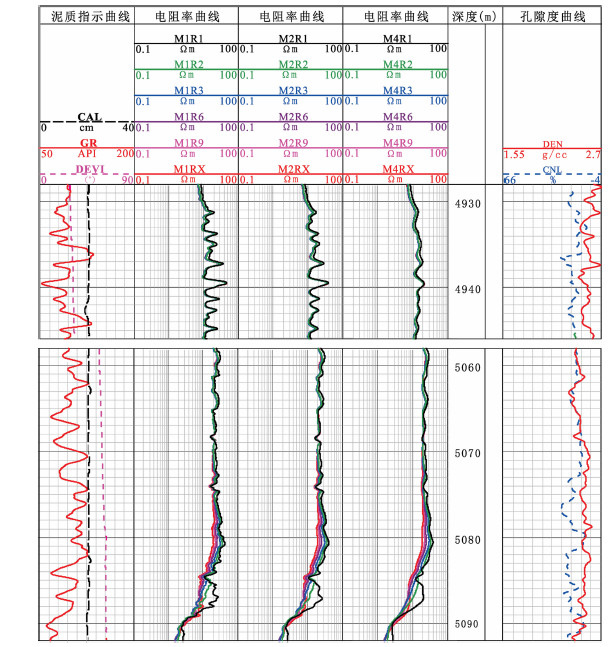
|
图 14 塔里木油田XX井HDIL测井成果图 Fig. 14 TheresultofHDILlogsforTarimoilfieldXX well |
至于偏心影响,由于无法判断仪器在井眼中的位置,因此无实例可供分析.
7 结论利用三维矢量有限元法分别对在各种井眼条件下的阵列感应测井原始响应进行了模拟,经过合成聚焦后形成测井曲线,对这些原始响应和测井曲线进行了分析,得到以下结论:
(1)已有的阵列感应测井数据处理中的一些模型假定是较为理想的,因此数据处理方法还存在一定缺陷.
(2)在不同井眼形状下,与圆形井眼相比,椭圆度越大,Rt/Rm越大,线圈距越短的原始测量信号所受的影响越大.相应地,合成聚焦后的测井曲线里浅探测曲线更易受椭圆度大小的影响.
(3)仪器偏心距越大,Rt/Rm越大,线圈距越短的原始测量信号所受的影响越大.相应地,合成聚焦后的测井曲线里浅探测曲线更易受仪器偏心的影响.
(4)斜井或倾斜地层对阵列感应测井结果的影响表现在地层视厚度和测量地层视电阻率两个方面.当井斜≤30°对视厚度基本没有影响,当井斜在30°~60°之间影响增大,井斜≥60°时不反映实际层厚;对测量地层视电阻率而言,井眼斜度对0.3和0.6 m的0.25 m探测曲线几乎没有影响,其它探测曲线在60°以内影响不大,60°以上相对误差急剧增大,而1.2 m阵列曲线受井斜影响相对较小,但与0.3和0.6 m相比,其相对误差较大.
(5)尽管阵列感应测井数据处理中已进行了井斜校正,但当井斜≥60°时,这种井斜校正还不完善,还必须进行进一步处理.
(6)在进行阵列感应测井仪器测井、资料处理以及资料解释时必须考虑井眼环境的影响,本方法及结果可为井眼环境影响的校正提供参考[23-26].
| [1] | Zhou Z Q, Geldmacher I M, Corley B H, et al. Stabilizing the shallow (10-inch) resolution matched curve of the high-definition-induction log and evaluating quality control for array induction logs. SPWLA 44th Annual Logging Symposium, 2003. |
| [2] | Geldmacher I M, Xiao J Q, Atlas B. Interpreting multl4rray induction logs in high Rt/Rs contrast environments with an inhomogeneous background-based software focusing method. SPWLA 40th Annual Logging Symposium, 1999. |
| [3] | Barber T D, Rosthal R A. Using a multiarray induction tool to achieve high-resolution logs with minimum environmental effects. SPE 22725, in SPE 66th Annual Technical Conference and Exhibition Proceedings, 1991. |
| [4] | Darling H, Barber T, Wu X W, et al. Interpreting multiarray induction logs in difficult environments. SPWLA 40th Annual Logging Symposium, 1999. |
| [5] | Gao G Z, Torres-Verdín C. Fast 3D modeling of borehole induction data in dipping and anisotropic formations using a novel approximation technique. SPWLA 44th Annual Logging Symposium, 2003. |
| [6] | 仵杰, 段雁超, 李凡, 等. 基于COMSOL仿真软件的阵列感应测井偏心响应计算方法. 测井技术 , 2012, 36(4): 357–360. Wu J, Duan Y C, Li F, et al. Computing the eccentric response of array induction logging based on COMSOL. Well Logging Technology (in Chinese) , 2012, 36(4): 357-360. |
| [7] | 陈爱新. 随钻电磁波测井环境影响分析. 石油地球物理勘探 , 2006, 41(5): 601–605. Chen A X. Analysis of environment influence in electromagnetic logging while drilling. Oil Geophysical Prospecting (in Chinese) , 2006, 41(5): 601-605. |
| [8] | 赵军龙, 李甘, 朱广社, 等. 低阻油层成因机理及测井评价方法综述. 地球物理学进展 , 2011, 26(4): 1334–1343. Zhao J L, Li G, Zhu G S, et al. Review of logging evaluating method and contributing factors or mechanism on low resistivity reservoirs. Progress in Geophysics (in Chinese) , 2011, 26(4): 1334-1343. |
| [9] | 张向林, 刘新茹, 李健, 等. 5频等参数阵列相位差感应电阻率. 地球物理学进展 , 2007, 22(5): 1562–1565. Zhang X L, Liu X R, Li J, et al. 5-Frequency isoparametric array induction resistivity logging tool. Progress in Geophysics (in Chinese) , 2007, 22(5): 1562-1565. |
| [10] | 原宏壮, 陆大卫, 张辛耘, 等. 测井技术新进展综述. 地球物理学进展 , 2005, 20(3): 786–795. Yuan H Z, Lu D W, Zhang X Y, et al. An overview of recent advances in well logging technology. Progress in Geophysics (in Chinese) , 2005, 20(3): 786-795. |
| [11] | 仵杰, 李博博, 解茜草, 等. 阵列感应测井响应的井洞影响分析. 测井技术 , 2011, 32(6): 498–502. Wu J, Li B B, Xie X C, et al. Analysis of the cave effect on the array induction logging response. Well Logging Technology (in Chinese) , 2011, 32(6): 498-502. |
| [12] | 沈金松. 用边有限元方法计算磁偶极子的三维电磁响应. 计算物理 , 2002, 19(6): 537–543. Shen J S. Modeling 3-D electromagnetic responses of the magnetic dipole in frequency domain by using the edge finite element method. Chinese Journal of Computational Physics (in Chinese) , 2002, 19(6): 537-543. |
| [13] | 梁灿彬, 秦光戎, 梁竹健. 电磁学. 北京: 高等教育出版社, 1985 . Liang C B, Qin G R, Liang Z J. Electromagnetics (in Chinese). Beijing: Higher Education Press, 1985 . |
| [14] | 金建铭. 电磁场有限元方法. 西安: 西安电子科技大学出版社, 1998 . Jin J M. Finite Element Method for Electromagnetic Field (in Chinese). Xi'an: Xidian University Press, 1998 . |
| [15] | 谭茂金, 张庚骥. 用模式匹配法计算电阻率测井响应研究进展. 地球物理学进展 , 2006, 21(1): 208–213. Tan M J, Zhang G J. Progress in numerical mode-matching method of electrical logs. Progress in Geophysics (in Chinese) , 2006, 21(1): 208-213. |
| [16] | 戴前伟, 陈德鹏, 刘海飞, 等. 双频激电井地电位技术研究剩余油分布. 地球物理学进展 , 2009, 24(3): 959–964. Dai Q W, Chen D P, Liu H F, et al. Research of the residual oil dstribution with dual frequency induced polarization and the borehole-to-surface potential method. Progress in Geophysics (in Chinese) , 2009, 24(3): 959-964. |
| [17] | 李传伟, 慕德俊, 李安宗. 双频介电测井方法与实现. 地球物理学进展 , 2007, 22(6): 1862–1866. Li C W, Mu D J, Li A Z. The method and compliment of dual frequency dielectric logging. Progress in Geophysics (in Chinese) , 2007, 22(6): 1862-1866. |
| [18] | 尹文禄, 邓聪, 赵菲, 等. 高阶矢量有限元方法实现及关键问题. 电波科学学报 , 2009, 24(2): 349–353. Yin W L, Deng C, Zhao F, et al. Implementation for higher order vector FEM and some key issues. Chinese Journal of Radio Science (in Chinese) , 2009, 24(2): 349-353. |
| [19] | 文世鹏. 应用数值分析. 北京: 石油工业出版社, 1999 . Wen S P. Applied Numerical Analysis (in Chinese). Beijing: Petroleum Industry Press, 1999 . |
| [20] | 王昌学, 周灿灿, 储昭坦, 等. 电性各向异性地层频率域电磁响应模拟. 地球物理学报 , 2006, 49(6): 1873–1883. Wang C X, Zhou C C, Chu Z T, et al. Modeling of electromagnetic responses in frequency domain to electrical anisotropic formations. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1873-1883. |
| [21] | 孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应. 地球物理学报 , 2008, 51(5): 1600–1607. Sun X Y, Nie Z P, Zhao Y W, et al. The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1600-1607. |
| [22] | 张中庆, 穆林雪, 张雪, 等. 矢量有限元素法在随钻电阻率测井模拟中的应用. 中国石油大学学报(自然科学版) , 2011, 35(4): 64–71. Zhang Z Q, Mu L X, Zhang X, et al. Application of vector finite element method to simulate logging-while-drilling resistivity tools. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2011, 35(4): 64-71. |
| [23] | 牒勇, 仵杰, 吕超英, 等. 阵列感应井眼校正中的一种快速正演方法. 测井技术 , 2009, 33(5): 411–414. Die Y, Wu J, Lü C Y, et al. A fast forward method for borehole correction in multi-array induction logging. Well Logging Technology (in Chinese) , 2009, 33(5): 411-414. |
| [24] | 刘振华, 仵杰, 张建华, 等. 阵列感应(AIT)测井响应的连续反演. 地球物理学进展 , 2006, 21(4): 1198–1201. Liu Z H, Wu J, Zhang J H, et al. Sequent inversion for the logging data of array induction tool (AIT). Progress in Geophysics (in Chinese) , 2006, 21(4): 1198-1201. |
| [25] | 刘迪仁, 谢伟彪, 袁继煌, 等. 二维复杂泥浆侵入阵列感应测井响应模拟与分析. 测井技术 , 2012, 36(3): 234–238. Liu D R, Xie W B, Yuan J H, et al. Simulation and analysis of array induction log response for complicated two-dimensional mud invasion. Well Logging Technology (in Chinese) , 2012, 36(3): 234-238. |
| [26] | 仵杰, 桂彩云, 解茜草. 阵列感应测井斜井信号处理方法研究. 石油仪器 , 2011, 25(2): 68–70. Wu J, Gui C Y, Xie X C. A method for processing dipping signals of multiarray induction logs. Petroleum Instruments (in Chinese) , 2011, 25(2): 68-70. |
 2013, Vol. 56
2013, Vol. 56

