微地震事件的准确定位是微地震监测研究的重要任务.影响精确定位的因素很多,主要包括速度模型建立、反演算法的适用性、正演算法的精度等方面[1-3].高精度的反演研究,目前还主要以时差反演为主,通过模型校正,反演方法的研究,来提高定位的精度,其中又分为P波时差反演、P-S波时差反演[4-5].
常规地震中,共轭梯度法、模拟淬火法、遗传算法等线性、非线性算法,都能够取得比较好的反演效果,但是,微地震反演中,由于信号的信躁比低,加上各种噪音的干扰,拾取的初至很难保证准确,使得单纯地移植这些反演方法难以取得效果.线性反演方法,一般来讲速度快,效率高,但是易于局部收敛,对设定的初值要求高.非线性方法,全局搜索能力强,但是算法设计比较复杂,反演参数越多,反演速度越慢[6].
遗传算法是一种在地球物理学领域应用比较广泛的非线性反演方法[7],其独有的个体、种群概念,保证了搜索的路径是多维的,可以避免陷入局部极值,但是,遗传操作过程中,主要算法参数的选择,对于反演结果的影响很大,既影响反演的速度,又影响反演的精度.在微地震事件反演中[8-9],如果任意定义反演的搜索范围,任意定义选择算子,交叉算子,变异算子,适应度函数,种群大小,遗传代数等等,那么遗传算法反演的效率与精度都会发生很大的变化,又增大了了反演结果的不稳定性.
本文针对遗传算法存在的问题,讨论了差分进化寻优方法.该算法具有以下特点:
(1)算法通用,不依赖于问题信息.
(2)群体搜索,具有记忆个体最优解的能力.
(3)协同搜索,具有利用个体局部信息和群体全局信息指导算法进一步搜索的能力.
(4)易于与其它算法混合,构造出具有更优性能的算法.
微地震信号信躁比低[10-11],拾取初至信息不准确,以往的确定性的线性或非线性反演方法不能取得可靠的反演结果[12-14].贝叶斯反演方法,是把先验信息和后验信息结合起来的推理估计方法,可以更好地融合多方面先验信息,实现后验信息的最佳估计,是不确定性数据资料常用的反演方法.利用贝叶斯最大后验估计理论进行反演方法研究,国内外已有许多文献报道,其中不乏微地震资料贝叶斯反演方法的文献[15].大都注重对后验信息更新估计方法的研究,对先验信息估计一般利用最大熵信息方法、共轭分布方法、均匀分布方法等,没有对先验信息的估计方法进行深入研究.实质上贝叶斯估计理论应用的有效性决定于先验信息的估计的有效性.本文从微地震模型资料分析出发,通过对模型资料抽样样本的统计特征分析,提出了先验信息的估计方法.围绕先验信息估计,对贝叶斯后验估计方法进行了研究,给出了加权系数的估计方法.最后形成了微地震资料贝叶斯框架下差分进化反演方法.理论模型和实际资料证明了研究方法对含噪音数据反演的有效性与可靠性.
2 贝叶斯估计方法 2.1 最大后验估计理论方法贝叶斯反演理论把反演问题与观测数据信息、模型信息以及先验信息通过贝叶斯推理联系起来.贝叶斯反演有多种求解方法,其中最常用的是贝叶斯最大后验解方法.设G为微地震到时观测数据,X为待反演参数,模型误差与待反演参数的先验估计均为正态分布,建立如下目标函数可得贝叶斯最大后验解[16]:
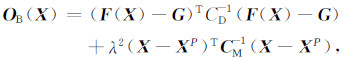
|
(1) |
式中,F(X)为模型结果,XP为参数的先验估计值,CD和CM为模型误差与先验估计误差的协方差矩阵,λ为权重系数,λ=CM/CD.目标函数OB(X)的求解,就是在数据拟合(第一项)和先验估计(第二项)之间寻求一种折衷.权重系数越大,反演解越接近先验估计;反之,反演解越接近于不稳定的原问题.实际求解时,首先选定若干λ的值并求得相应的反演解,然后根据λ与反演解的值计算目标函数OB(X)最小值对应的λ即为最佳权重系数.
对反演参数(速度、震源位置)的最优估计问题,等价于在贝叶斯理论下,具有先验信息条件时,经过贝叶斯推理,得到目标函数的极大后验概率.从公式(1)中看到,目标函数的极大后验概率,是理论模型和观测值残差、模型参数的参差极大后验概率的加权组合.实现时,通过模型反演得到位置参数和速度参参差结果的先验分布,然后确定参数的后验密度.
3 差分进化寻优方法 3.1 差分进化基本方法公式(1)中右边第一项是一个有关地层速度和震源位置的多变量函数,需要采用非线性法全局搜索算法来优化.为提高计算效率,采用差分进化寻优方法(简称DE方法)[17-18].
DE算法采用实数编码方式,其原理与遗传算法十分相似,进化流程包括:变异、交叉和选择.DE算法中的选择策略通常为和一对一的竞争生存策略,而交叉操作方式与遗传算法也大体相同,但在变异操作方面使用差分策略,即利用种群中个体间的差分向量对个体进行扰动,实现个体变异.
算法首先在问题的可行解空间随机初始化种群
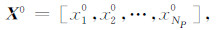
|
(2) |
NP为种群规模.个体X0=[x10,x20,…,xNP0]用于表征待求问题解,D为待求问题解的维数.对当前种群进行变异和交叉操作产生另一个新种群,然后利用基于贪婪思想的选择操作对这两个种群进行一对一的选择,从而产生最终的新一代种群.具体而言,首先通过式(2)对每一个在t时刻的个体xit实施变异操作,得到与其相对应的变异个体vit+1,即

|
(3) |
其中:r1,r2,r3 ∈{1,2,…NP }互不相同且与i不同;xr1t为父代基向量;(xr2t -xr3t)称作父代差分向量;K为缩放因子.然后利用式(3)对xit和由式(2)生成的变异个体vit+1进行交叉操作,生成实验个体uit+1,即
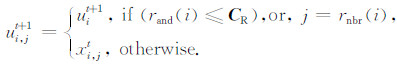
|
(4) |
其中:rand(j)为[0, 1]之间的交叉概率;rnbr(i)为{1,2,…,D}之间的随机量.利用式(4)对实验个体uit+1和xit的目标函数进行比较,选择更优的个体作为新种群的个体xit+1,即
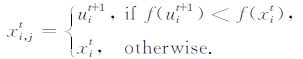
|
(5) |
其中,f为目标函数,CR为交叉因子.
3.2 群体规模的选择种群规模越大,搜索到全局最优解的可能性就越大[14-15],然而所需的计算量和计算时间也要增加.当种群规模增大到一定个数时,解的精度不再提高,甚至会出现降低的情况.因此,当种群规模太大时,如果不增加最大进化代数,精度反而会降低.另外,种群规模越大,多样性就越大,所以如果种群过早收敛,就要增加种群规模以增加多样性.在给定最大进化代数情况下,对低维简单问题,种群规模在[15, 35]之间较好;对高维复杂问题,种群规模在[30, 50]之间时,优化结果较好.总之,在给定最大进化代数下,种群规模在[15, 30]之间时,能很好地保持多样性和收敛速度的平衡.
3.3 缩放因子K对优化效果的影响缩放因子K取值[0.5,1]之间时,算法得到的结果较好;当K < 0.5或K>1时,算法求得的解的质量不高.当K较大时,差分向量对变异个体V的影响较大,能产生较大的扰动,从而有利于保持种群的多样性;反之,K较小时,扰动较小,缩放因子能起到局部精细化搜索的作用.因此,K对种群的多样性起到了一定的调节作用.缩放因子K取值太大,虽然能保持种群多样性,但算法近似随机搜索,搜索效率低,求得的全局最优解精度低;反之,K太小,种群多样性丧失很快,算法易于陷入局部最优出现早熟收敛[16-17].
交叉因子CR对优化效果的影响.CR的值较小时,所需的函数评价次数较大,收敛速度较慢,但成功率较高,算法的稳定性好;CR的值较大时,常常会加速收敛,但易于陷入局部最优,发生早熟现象,达到给定精度的成功率低,稳定性差.可见,成功率和收敛速度是一对矛盾.因此,为了同时保证较高的成功率和较快的收敛速度,对于单峰函数,CR取值相对较大些,在[0.6,0.8]区间;对其他复杂、多峰函数CR取值应相对小些,在[0.1,0.5]区间.
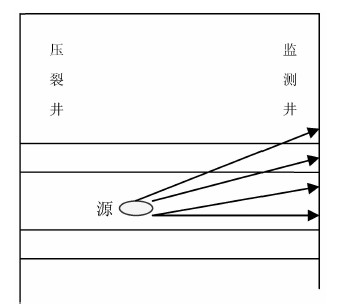
4 基于理论模型分析的实现方法研究 4.1 理论模型初至和初至差计算采用图 1所示的观测系统进行模型走时的计算.建立如表 1所示的水平层状速度模型.16级检波器中第一级的位置时(0,2415m),每级检波器之间的垂直距离是10 m,第16级检波器位置是(0,2565m).源的位置径向和纵向坐标为(691m,2620m)采用射线追踪方法,生成16道微地震走时初至和走时初至差结果如图 2和图 3.
|
图 1 井中微地震监测观测系统示意图 Fig. 1 Schematic diagram of well microseismic monitoring observation system |
|
|
表 1 水平层状速度模型 Table 1 Horizontally layered velocity model |

|
图 2 理论模型初至 Fig. 2 Theoretical model for first arrival |

|
图 3 理论模型初至差 Fig. 3 Theoretical model for first arrival difference |
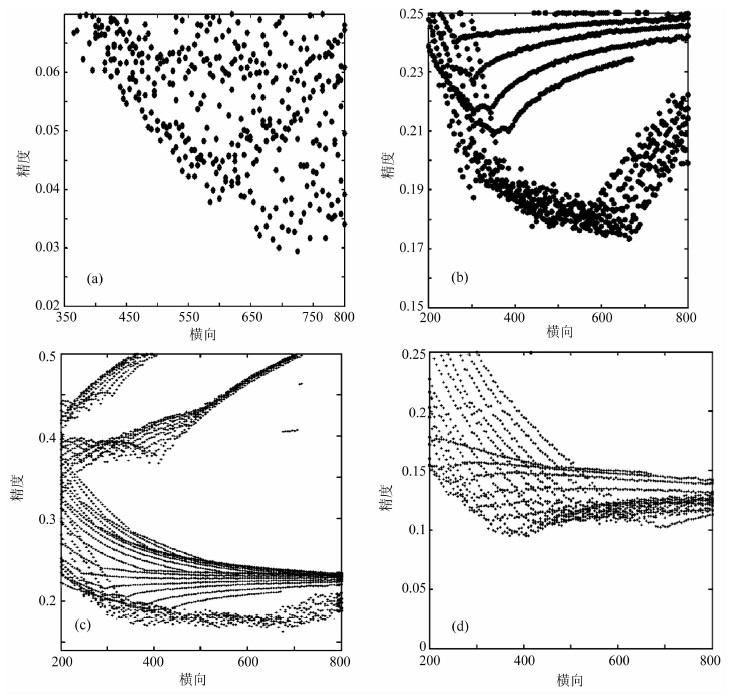
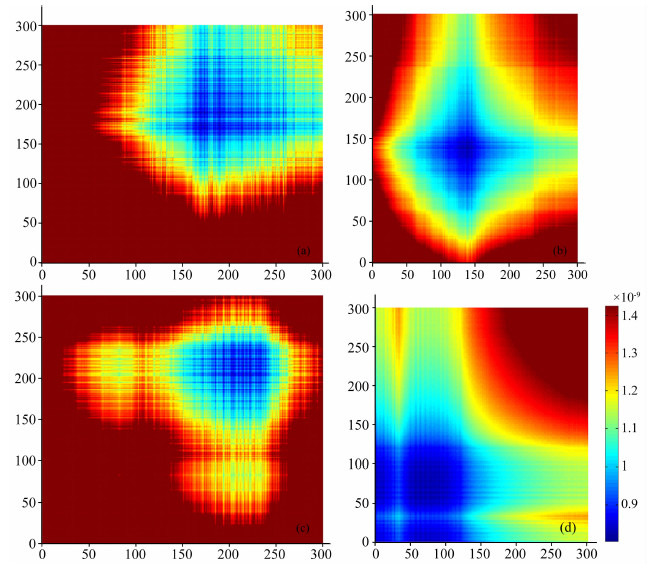
基于贝叶斯估计推理的关键是先验信息估计,一般先验信息的估计有最大熵方法、样本统计方法、均匀分布方法等,本文研究基于模型分析的先验信息确定方法.利用网格搜索方法对理论模型及不同噪音模型进行走时正反演计算,网格距为2m,其残差分布如图 4所示,从残差分布只能确定有无收敛解及收敛解的位置,不能确定判断收敛解是否真解并对真解进行估计.残差的协方差分布如图 5所示.分析图 5残差的协方差分布及和真解的对应关系看到,对于一维层状模型,微地震反演残差分布在真解附近范围内,呈对称分布(正态分布)(图 5a).
|
图 4 理论模型解误差分布 (a)不加噪音;(b)加5%噪音;(c)加20%噪音;(d)加40%噪音.图中纵坐标是残差,单位:m,横坐标为网格数. Fig. 4 Theoretical model of error distribution (a)Without noise; (b)5% noise; (c)20% noise; (d)40% noise |
|
图 5 理论模型解误差的协方差分布 (a)不加噪音;(b)加5%噪音;(c)加20%噪音;(d)加40%噪音;图中纵、横坐标为网格数. Fig. 5 A theoretical model for error covariance distribution (a)Without noise; (b)5% noise; (c)20% noise; (d)40% noise; The figure is the vertical and horizontal grid number. |
对初至加不同程度的噪音后,最小残差点不在真解位置,发生了偏移,见图 5b,5c,5d.最小残差点向真解的左下方位置移动.同时看到残差出现不对称分布,类似‘鞍形’分布,开口向着右上方(图 5b),并且以最小残差为中心向右上方和右下方逐渐增大变化,梯度变化小,并且托尾较长;相反,如果最小残差点向真解得右上方移动,残差分布呈现出以最小残差点开始,向左上方和左下方逐渐增大变化,梯度变化小,并且托尾较长.残差出现不对称分布,类似‘鞍形’分布,开口向着左下方(图 5c).
4.2.2 解先、后验信息估计根据上述讨论的残差、残差协方差分布特征和解的变化关系,可以给出确定真解范围的先验信息估计.当在给定的区域内解收敛时,找出残差最小时的解Xmin(初始先验信息),然后以初始先验解开始向着误差梯度减小的方向(即误差分布托尾长的一侧取值)取估计解(估计先验信息),表示为
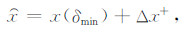
|
(6) |
x(δmin)表示最小残差对应的初始先验解,Δx+表示从最小残差对应的位置点向着残差梯度变化小的方向所取的距离.
在算法实现时,由于差分进化初始解在一小段范围内取种子解,因此给出先验解估计范围,表示为
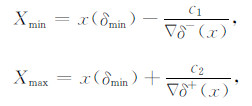
|
(7) |
Xmin,Xmax表示种子解的最小和最大范围,▽δ-(x)和▽δ+(x)分别表示最小残差点两侧的残差的梯度,c1,c2为系数.
通过不断地更新迭代,当达到真解时,则满足
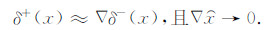
|
(8) |
贝叶斯最大后验估计公式中,加权系数是残差的协方差和先验信息解协方差的比值.然而先验解信息的协方差难以估计.从模型抽样分布特征研究得到,在向真解逼近的过程中,残差最小点两侧的残差梯度趋于相等.说明残差梯度比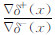
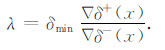
|
(9) |
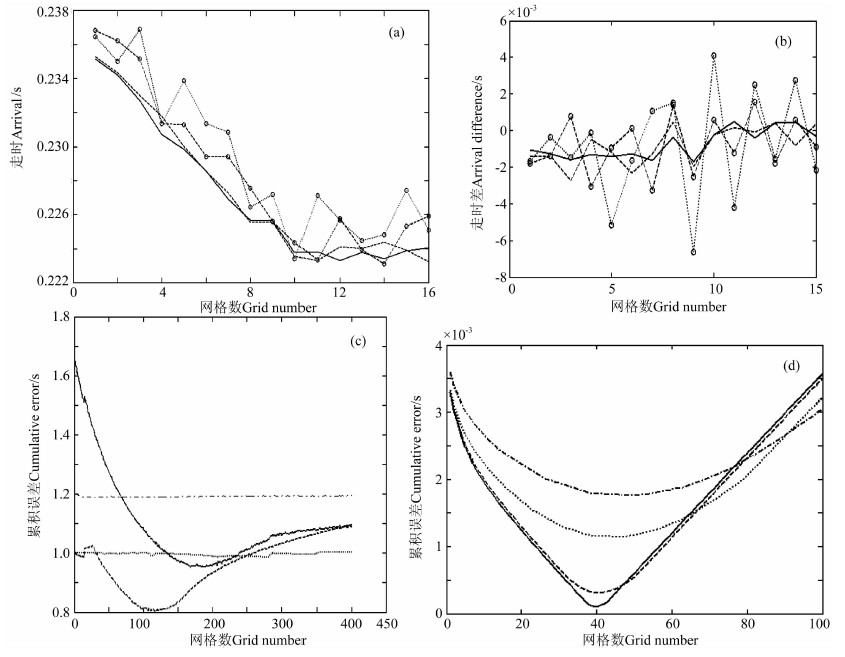
最大后验公式变换为
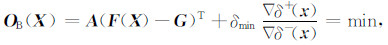
|
(10) |
其中
(1)计算理论模型初至和加噪初至,利用网格搜索方法求取反演残差,通过分析残差与残差协方差的分布特征,确定问题先验信息解.
(2)利用公式(6)进行先验信息解估计.
(3)在根据公式(7)确定先验信息范围内,选取差分进化方法的种子解,并进行解的寻优计算,同时给出种子解范围内的残差和残差的协方差.
(4)根据公式(9)计算加权系数.
(5)计算残差对解空间导数,形成雅可比矩阵.
(6)根据公式(10)计算最大后验估计.
(7)更新计算,当在满足(8)式条件下,由(10)式更新计算结果达到最小时,则计算过程结束,否则重复步骤(3)-(7).
6 模型测试结果对以上理论模型初至加4种上不同程度扰动噪音,分别加2、4、7、9个采样点,采样率为0.5ms,对应的走时扰动分别为1 ms、2 ms、3.5 ms、4.5 ms,得到4条加噪初至曲线,图 7a的实线、虚线、带‘°’的实线及带‘°’虚线,对应的4条初至差曲线,图 7b,的实线、虚线、带‘°’的实线及带‘°’虚线.设定纵向搜索范围大致在真解位置附近固定不变.
|
图 6 不同扰动噪音后的搜索法和本方法结果比较 (a)加不同噪音初至;(b)对应的图a初至差;(c)搜索方法结果;(d)本文方法结果. Fig. 6 Camparison of different disturbance noise by the search method and the method of this paper (a)With different noise to first arrival; (b)The corresponding first arrival difference; (c)Search method; (d)Method in this paper. |
|
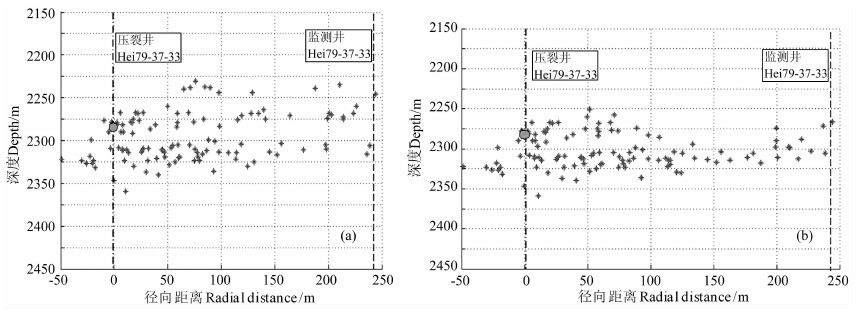
图 7 反演结果比较 (a)搜索方法结果;(b)本文方法结果. Fig. 7 Comparison of inversion results Search method results (a) and (b) the results method of this paper. |
图 7c为搜索法反演结果,径向搜索范围200~1700m,搜索步长为2 m.图中显示范围是250~1050m(对应的网格数是1~400).真解位置是691m,对应图 7c第245个样点附近.对于初至2、3个采样点扰动时,估计解的位置和真解位置差距较大,收敛极小点位置分别位于第190个样点(650 m)和第110个样点(470m),与真解(第245个样点)的误差分别41m和221m.对于初至5、9个采样点扰动时没有收敛解.
图 7d图为本文方法结果,显示范围50~1550m(对应的网格数是1~100),横坐标样点距为15m.对于初至2、3个采样点扰动时,估计解的位置和真解位置差距较小,收敛的极小点位置分别位于第42个样点(680 m)和第44个样点(710 m),与真解误差分别为10m和20 m.对于初至5、9个采样点扰动时仍有收敛解.
7 实际资料的反演结果比较分析实际微地震资料为国内某地区Hei-79-37-33井作为监测井、Hei-79-37-31井作为压裂井采集的微地震数据,两口井的水平距离为298.0m,考虑到地层起伏变化相对较小,结合两口井的测井资料建立速度模型.依次进行射孔反演速度模型校正、有效事件识别、震相识别工作后,然后对实际微地震资料进行反演.为了验证反演方法解决实际问题的效果,同时进行了搜索法反演,从结果看到本文方法反演结果比搜索方法反演结果更加聚团收敛,并且和实际期望压裂方案一致.结合当地的地质资料及开发资料判断分析其反演结果是合理正确的(见图 7).
8 结论利用网格搜索方法对不同噪音模型初至进行正反演,计算得到的残差分布只能确定有无收敛解及收敛解的位置,不能对真解进行估计.残差的协方差分布,能够对真解进行估计.利用残差协方差极小点位置移动、分布梯度变化,可以进行解先验信息估计.针对后验估计中,由于难以获得解空间的方差估计致使无法计算加权系数问题,通过分析残差变化特征和解的变化关系,研究的求取权系数方法,测试结果证明方法是可行的.
差分进化(DE)的变异方式,有效利用群体分布特性,提高算法的搜索能力,避免遗传算法中变异方式的不足.对于DE算法,在给定最大进化代数下,种群规模在[15, 30]之间时,能很好地保持多样性和收敛速度的平衡.为了同时保证较高的成功率和较快的收敛速度,对于单峰函数,交叉因子CR取值相对较大些;对其它复杂、多峰函数交叉因子CR取值应相对小些.
通过理论和实际论证和验证了研究方法的正确合理性,并和网格搜索方法反演结果进行了对比分析,证明本文研究的反演方法精度高于搜索方法.
致谢本文研究得到了中石化科技部、中石化胜利物探公司和中石化南京物探研究院的支持和帮助,谨表示真诚的感谢!
| [1] | 徐果明. 反演理论及其应用. 北京: 地震出版社, 2003 . Xu G M. Inversion Theory and Application (in Chinese) (in Chinese). Beijing: Seismological Press, 2003 . |
| [2] | 刘希强, 周彦文, 曲均浩, 等. 应用单台垂向记录进行区域地震事件实时检测和直达P波初动自动识别. 地震学报 , 2009, 31(3): 260–271. Liu X Q, Zhou Y W, Qu J H, et al. Real-time detection of regional events and automatic P-phase identification from the vertical component of a single station record. Acta Seismologica Sinica (in Chinese) (in Chinese) , 2009, 31(3): 260-271. |
| [3] | 宋维琪, 杨晓东. 基于射线追踪的微地震多波场正演模拟. 地球物理学进展 , 2012, 27(4): 1501–1508. Song W Q, Yang X D. The multi-wave field forward simulation of micro-seismic based on ray tracing. Progress in Geophysics (in Chinese) (in Chinese) , 2012, 27(4): 1501-1508. |
| [4] | 吴治涛, 骆循, 李仕雄. 联合小波变换与偏振分析自动拾取微地震P波到时. 地球物理学进展 , 2012, 27(1): 131–136. Wu Z T, Luo X, Li S X. United wavelet transform and polarization analysis automatically identify micro seismic P-arrival. Progress in Geophysics (in Chinese) (in Chinese) , 2012, 27(1): 131-136. |
| [5] | 吴治涛, 李仕雄. STA/LTA算法拾取微地震事件P波到时对比研究. 地球物理学进展 , 2010, 25(5): 1577–1582. Wu Z T, Li S X. Comparison of STA/LTA P-pickers for micro seismic monitoring. Progress in Geophysics (in Chinese) (in Chinese) , 2010, 25(5): 1577-1582. |
| [6] | 宋维琪, 刘军, 陈伟. 改进射线追踪算法的微震源反演. 物探与化探 , 2008, 32(3): 274–278. Song W Q, Liu J, Chen W. Microearthquake source inversion of an improved ray tracing algorithm. Geophysical and Geochemical Exploration (in Chinese) (in Chinese) , 2008, 32(3): 274-278. |
| [7] | 吴涛, 李红星, 陶春辉, 等. 基于改进遗传算法的BISQ模型多参数反演方法研究. 地球物理学进展 , 2012, 27(5): 2128–2137. Wu T, Li H X, Tao C H, et al. The methodological study of multi-inversion of BISQ mold parameters based on modified genetic algorithm. Progress in Geophysics (in Chinese) (in Chinese) , 2012, 27(5): 2128-2137. |
| [8] | 刘建中, 王春耘, 刘继民. 用微地震法监测油田生产动态. 石油勘探与开发 , 2004, 31(2): 71–73. Liu J Z, Wang C G, Liu J M. Micro-seismic monitor on the operation of oil fields. Petroleum Exploration and Development (in Chinese) (in Chinese) , 2004, 31(2): 71-73. |
| [9] | 屈永华, 王锦地, 刘素红, 等. 贝叶斯网络支持的地表参数混合反演模式研究. 遥感学报 , 2006, 10(1): 6–14. Qu Y H, Wang J D, Liu S H, et al. Study on hybrid inversion scheme under bayesian network. Journal of Remote Sensing (in Chinese) (in Chinese) , 2006, 10(1): 6-14. |
| [10] | 张山, 刘清林. 微地震监测技术在油田开发中的应用. 石油物探 , 2002, 41(2): 226–231. Zhang S, Liu Q L. Application of microseismic monitoring technology in development of oil field. Geophysical Prospecting for Petroleum (in Chinese) (in Chinese) , 2002, 41(2): 226-231. |
| [11] | 朱卫星, 张春晓, 邱铁成, 等. 微地震信号的变速FK滤波-自适应极化滤波方法. 地球物理学进展 , 2009, 24(5): 1776–1786. Zhu W X, Zhang C X, Qiu T C, et al. The seismic signal technology with variable velocity FK filtering-the auto-adapted polarization filtering. Progress in Geophysics (in Chinese) (in Chinese) , 2009, 24(5): 1776-1786. |
| [12] | 陈旭庚, 王恩福, 李晓东, 等. 基于微震监测技术的田野文物防盗方法研究. 地球物理学进展 , 2008, 23(6): 1975–1982. Chen X G, Wang E F, Li X D, et al. Investigation on the safeguarding method of the field tumulus by the micro-seismic monitoring technique. Progress in Geophysics (in Chinese) (in Chinese) , 2008, 23(6): 1975-1982. |
| [13] | De Meersman K, Kendall J M, van der Baan M. The 1998 Valhall microseismic data set:An integrated study of relocated sources, seismic multiplets, and S-wave splitting. Geophysics , 2009, 74(5): B183-B195. DOI:10.1190/1.3205028 |
| [14] | Chunduru R K, Sen M K, Stoffa P L. Hybrid optimization methods for geophysical inversion. Geophysics , 1997, 62(4): 1196-1207. DOI:10.1190/1.1444220 |
| [15] | 詹海刚, 施平, 陈楚群. 基于贝叶斯反演理论的海水固有光学特性准分析算法. 科学通报 , 2006, 51(2): 204–210. Zhan H G, Shi P, Chen C Q. Based on Bayesian inversion theory of inherent optical properties of seawater analysis algorithm. Chinese Science Bulletin (in Chinese) (in Chinese) , 2006, 51(2): 204-210. |
| [16] | 苑闻京. 叠前反演和地震吸收技术在复杂天然气藏地震预测中的应用. 地球物理学进展 , 2012, 27(3): 1107–1115. Yuan W J. Application of pre-stack seismic inversion and seismic absorption technology for forecasting of complex gas reservoir. Progress in Geophysics (in Chinese) , 2012, 27(3): 1107-1115. DOI:10.6038/j.issn.1004-2903.2012.03.035. |
| [17] | 李维国, 同登科. 数值计算方法. 东营: 中国石油大学出版社, 2009 . Li W G, Tong D K. Numerical Calculation Method (in Chinese) (in Chinese). Dongying: China University of Petroleum Press, 2009 . |
| [18] | 万永革, 李鸿吉. 遗传算法在确定震源位置中的应用. 地震地磁观测与研究 , 2005, 16(6): 1–7. Wan Y G, Li H J. The preliminary study on the seismic hypocenter location using genetic algorithms. Seismological and Geomagnetic Observation and Research (in Chinese) (in Chinese) , 2005, 16(6): 1-7. |
| [19] | Moser T J. Shortest path calculation of seismic rays. Geophysics , 1991, 56(1): 59-67. DOI:10.1190/1.1442958 |
| [20] | Prugger A F, Gendzwill D J. Microearthquake location:A nonlinear approach that makes use of a simplex stepping procedure. Bull. Seism. Soc. Am. , 1988, 78(2): 799-815. |
| [21] | Stoffa P L, Sen M K. Nonlinear multiparameter optimization using genetic algorithms:Inversion of plane-wave seismograms. Geophysics , 1991, 56(11): 1794-1810. DOI:10.1190/1.1442992 |
| [22] | Dumay J, Fournier F. Multivariate statistical analyses applied to seismic facies recognition. Geophysics , 1988, 53(9): 1151-1159. DOI:10.1190/1.1442554 |
| [23] | 陈旭庚, 王恩福, 李晓东, 等. 基于微震监测技术的田野文物防盗方法研究. 地球物理学进展 , 2008, 23(6): 1975–1982. Chen X G, Wang E F, Li X D, et al. Investigation on the safeguarding method of the field tumulus by the micro-seismic monitoring technique. Progress in Geophysics (in Chinese) (in Chinese) , 2008, 23(6): 1975-1982. |
| [24] | Engell-Sorensen L. Inversion of Arreal times of microearthquake sources in the noth sea using a 3-D velocity structure and prio information. PART I. Method. Bulletin of the Seismological Society of America , 1991, 81(4): 1183-1194. |
| [25] | Pei D H, Quirein J A, Cornish B E, et al. Velocity calibration for microseismic monitoring:A very fast simulated annealing (VFSA) approach for joint-objective optimization. Geophysics , 2009, 74(6): WCB47-WCB55. DOI:10.1190/1.3238365 |
| [26] | 程勃, 底青云. 基于遗传算法和统计学的电阻率测深二维反演研究. 地球物理学进展 , 2012, 27(2): 788–795. Cheng B, Di Q Y. 2D inversion of resistivity sounding base on GA and statistic method. Progress in Geophysics (in Chinese) (in Chinese) , 2012, 27(2): 788-795. |
| [27] | 文成哲, 刘财, 郭智奇, 等. 遗传算法和LM算法联合反演瑞雷波相速度. 地球物理学进展 , 2010, 25(1): 303–309. Wen C Z, Liu C, Guo Z Q, et al. Joint inversion of Rayleigh wave phase velocity by GA and Levenberg-Marquardt (LM) algorithm. Progress in Geophysics (in Chinese) (in Chinese) , 2010, 25(1): 303-309. |
| [28] | Jupe A, Cowles J, Jones R. CSM, Associates Ltd. , Penryn, Cornwall, UK. Micro-seismic Monitoring. Listen and see the reservoir. World Oil , 2000, 12: 171-173. |
| [29] | Dyer B C, Jones R H, Cowles J F. Microseismic survey of a North Sea reservoir. World Oil , 1999, 5: 74-78. |
| [30] | Phillips W S, House L S. Micro-seismic mapping of a Cotton Valley Hydraulic Fracture using decimated downhole arrays. International Exposition and Sixty Eighth Annual Meeting , 1998, 9: 13-18. |
| [31] | 柳建新, 童孝忠, 杨晓弘, 等. 实数编码遗传算法在大地电磁测深二维反演中的应用. 地球物理学进展 , 2008, 23(6): 1936–1942. Liu J X, Tong X Z, Yang X H, et al. Application of real coded genetic algorithm in two-dimensional magnetotelluric inversion. Progress in Geophysics (in Chinese) (in Chinese) , 2008, 23(6): 1936-1942. |
| [32] | R??ek B, Kvasni?ka M. Differential evolution algorithm in the earthquake hypocenter location. Pure Appl. Geophys. , 2001, 158(4): 667-693. DOI:10.1007/PL00001199 |
| [33] | Leidenfrost A, Ettrich N, Gajewski D, et al. Comparison of six different methods for calculating traveltimes. Geophysical Prospecting , 1999, 47(3): 269-297. DOI:10.1046/j.1365-2478.1999.00124.x |
 2013, Vol. 56
2013, Vol. 56


