以GPS技术为代表的空间大地测量技术用于大规模连续地壳形变监测至今已有近20年的时间.随着GPS技术的不断成熟和完善, 人们对其的研究重点已从传统的观测模型、位置获取、速度估计等转移到了更深层次的时序特征分析、噪声序列分析、不同(时空)尺度误差模型精化等层面上来.其中, 基于GPS坐标时间序列的观测噪声特性的分析和提取研究打破了人们对传统噪声序列仅含高斯白噪声且随机独立的认识局限, 为优化随机模型建模、位移场/速度场误差统计、台站选址建设等提供了更明确的指导依据.基于连续GPS时间序列的噪声特性分析研究大致始于20世纪90年代末, Langbein ZhangJie, Mao, Williams等[1-2]的研究成果对该领域的贡献最为显著, 其结论大致可归纳为:各站的GPS残差序列在空间和时间上并不完全独立; 除白噪声外, 还含有明显的幂律噪声成分; GPS残差序列中的幂律噪声成分主要为闪烁噪声或随机游走噪声; 对于全球分布的测站, 其噪声特性可使用"白噪声+闪烁噪声"模型进行较好描述; 区域站的长期谱指数变化普遍比全球站更加显著; 幂律噪声的存在将致使传统GPS数据处理成果的误差统计特性明显偏优.具体而言, Langbein等[1-2]对南加利福尼亚州10个GPS连续运行参考站的近19个月的坐标序列进行了分析, 发现"白噪声+闪烁噪声"组合模型可以最好地匹配各个站的噪声特性; Mao等[3]对全球分布的23个GPS连续运行参考站的近3年观测数据进行了时序分析, 得出了类似结论, 并发现垂向噪声分量的大小与测站所在经度有明显的关联; Calais等[4]对位于欧洲的3个GPS测站进行了同样分析, 也得到了类似的结论; Bock等[5]对高频(1~30s)GPS时间序列的分析也表明, 即使在高频序列中, 也仍然含有明显的幂律噪声; Johnson等[6-7]分别对因土壤和天气因素引起的GPS随机游走噪声进行了探测和分析, 通过对PFO计划中的50个月长的GPS数据分析表明, 随机游走噪声的尺度可以达到3mm/yr1/2; .文献[2-3, 8-9]等针对上述各种幂律噪声对速度场信息估计的影响, 进行了详细分析并给出了估计公式.Williams等[8]拓展了上述学者的研究思路, 解除了对谱指数估计中的整数特性约束, 将其作为未知量与其他参数一同解算, 并对全球414个站的954个连续坐标序列进行了无约束MLE估计, 除上述类似结论外, 其还得出:对于全球解, 其白噪声分量呈现明显的纬度相关, 并且在赤道处达到最大; 闪烁噪声呈现类似的特性, 但不如白噪声明显; 南半球测站的噪声水平为白噪声约1~2 mm, 闪烁噪声约2~4mm/yr1/4.
基于GPS坐标序列的噪声特性分析尽管取得了大量的进展, 但不难发现, 上述研究成果均是建立在对连续、平稳的GPS坐标序列分析的基础之上的, 对于显著的因大地震等事件引起的非平稳坐标序列, 则关注较少, 或者往往采用先计算同震形变, 以此去除掉地震前后序列中的系统差异, 之后将拼接后的坐标序列等同于常规序列进行相关处理, 这样的方法虽然简单, 但依据我们的研究发现, 这种做法并不可取!本文基于四川GPS连续观测网络在汶川地震前后近10年(2003-2012年)的历史数据, 对因2008年汶川5.12特大地震引起的地震前后均约5年的GPS坐标序列时空演化特性进行对比和统计分析, 阐述了传统方法的问题所在, 并结合速度场变化趋势等背景场信息对相关成果进行了物理解析.
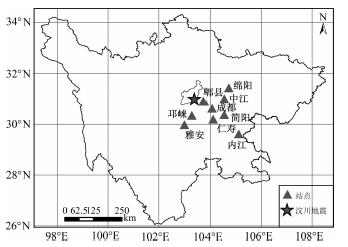
2 GPS时间序列的获取及其噪声特性分析方法本次研究的数据平台主要来自于四川GPS连续运行参考站网络, 该网络始建于2003年, 目前共由63个站组成(本次试验中, 我们重点选取了拥有最长观测历史的约9个测站进行研究, 如图 1所示, 其他测站的数据则主要用以实验成果验证和综合背景场分析), 已基本实现对四川48万平方公里范围内的全域连续覆盖, 其中, 汶川地震是四川CORS网络建成以来捕获的第一次重大地震事件.
|
图 1 实验网络及汶川地震震中位置分布图 Fig. 1 The location of GPS network and epicenter of the Wenchuan earthquake |
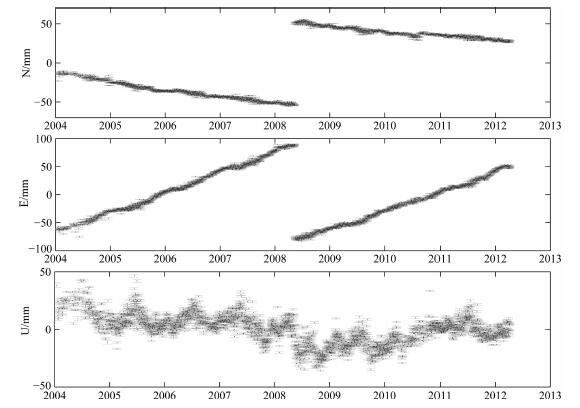
四川GPS观测网络的数据统一采用GAMIT/ GLOBK软件进行解算, 同时, 为了最大限度地确保共模误差的估计有效性, 避免区域物理背景信息提取中可能因强约束带来的不利影响, 网络平差统一采用全球平差(以成都为例, 平差结果见图 2). GAMIT/GLOBK软件解算的具体步骤和精度评定方法已有大量文献出版, 本文不再赘述.
|
图 2 成都(CHDU)站坐标序列(2004-2012) Fig. 2 Time series of CHDU site(2004-2012) |
对于GAMIT/GLOBK平差后获取的GPS坐标时间序列, 我们采用最大似然估计(Maximum LikelihoodEstimator, 简称MLE)方法对其进行噪声特征分析, 基本原理如下:
假定坐标序列为x(ti), 其横轴截距为x0, 速度分量为r, 量测误差为ε, 则有:
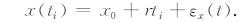
|
(1) |
与绝大多数地球物理观测量相同, GPS坐标序列中的噪声特性符合幂律过程(power law process)[2, 8], 其在时间域内的功率谱特征具有如下形式:
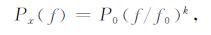
|
(2) |
其中, f为时间频率, P0和f0为标准化常量, k为谱指数, 对于GPS等大多数地球物理量而言, -3 < k < 1.其中, k=-1时, 称为闪烁噪声, 当k=-2时, 称为随机游走噪声, 当k=0时, 称为白噪声.为统一起见, 除白噪声外, 其他噪声也可被称为幂律噪声.
由此, 我们可假定误差项εx(t)的向量形式ε(t)是由一组标准差为a的白噪声α和标准差为bk的幂律噪声β组成, 其中, εx(t), a, bk单位为mm, 即:

|
(1) |
根据公式(1), 可得观测量x(ti)的协方差矩阵为:
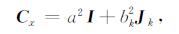
|
(3) |
其中, I为单位阵, Jk为相应幂律噪声的协方差矩阵.Jk的构造是MLE算法中的关键步骤之一, 文献[2](pg.18052-18054)、[8]等分别就各类幂律噪声的协方差矩阵构造方法进行了讨论, 篇幅限制, 本文不再赘述.
为了估计上述噪声水平分量, 可通过迭代调整Cx, 使得下述概率函数值达到最大:
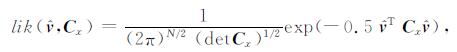
|
(4) |
其中, lik为似然值, det为矩阵的秩, N为观测历元, 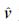
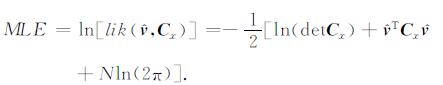
|
(5) |
最大似然估计问题的典型解决方案为下降单纯形法(thedownhillsimplexmethod)[10], williams对该算法进行了有效的改进[8, 11], 本文的算法即是在其基础上实现的.
需要说明的是, MLE算法可同时估计多种高斯随机噪声分量, 比如白噪声、幂律噪声、一阶高斯马尔科夫噪声、自回归噪声、移动平均噪声等, 在本文中, 我们只分析两类经典噪声, 即白噪声和幂律噪声; 同时, x(ti)中除可包含横轴截距、速度等线性信息外, 还可以包含多种非线性信息, 最典型的非线性信息主要包含年变化和半年变化周期信息, 作者在编制该算法时一并对其进行了考虑.
3 试验成果与分析为了研究地震事件对GPS坐标序列的影响, 我们以发震时间为参考, 将地震前后的测站坐标序列分为两段, 即地震前和地震后坐标序列.对两段序列, 分别使用MLE方法对其横轴截距、速率、年周期变化、半年周期变化、白噪声、幂律噪声等进行估计, 其中, 因幂律噪声的估计方式不同, 又可将相应成果分为两类, 一类为将幂律噪声的谱指数k人为约束为整数时得到的对比分析结果, 即整数谱指数分析成果; 另一类为不进行任何约束得到的分析结果, 即任意谱指数分析成果.
另外, 前期的研究成果表明, 对于区域网而言, 共模误差的存在将显著影响观测序列的噪声特性分析, 因此, 本文的后续实验内容均包含了共模误差消除前后的相关成果对比分析.需要说明的是, 传统的共模误差消除方法[12-13], 通常建议先估计测站位移速度, 并以此消除序列中的系统变化趋势, 但作者的实验发现, 该种方法不仅费力, 而且通常会干扰处理效果, 尤其对于存在非线性趋势的坐标序列, 其劣势更为明显, 因此, 作者在对四川区域GPS观测网络进行共模误差消除时, 不再进行"趋势消除(detrending)"操作, 而是直接在原始坐标序列的基础上进行堆栈(stacking)和滤波(filtering)处理, 篇幅限制, 本文不再赘述.
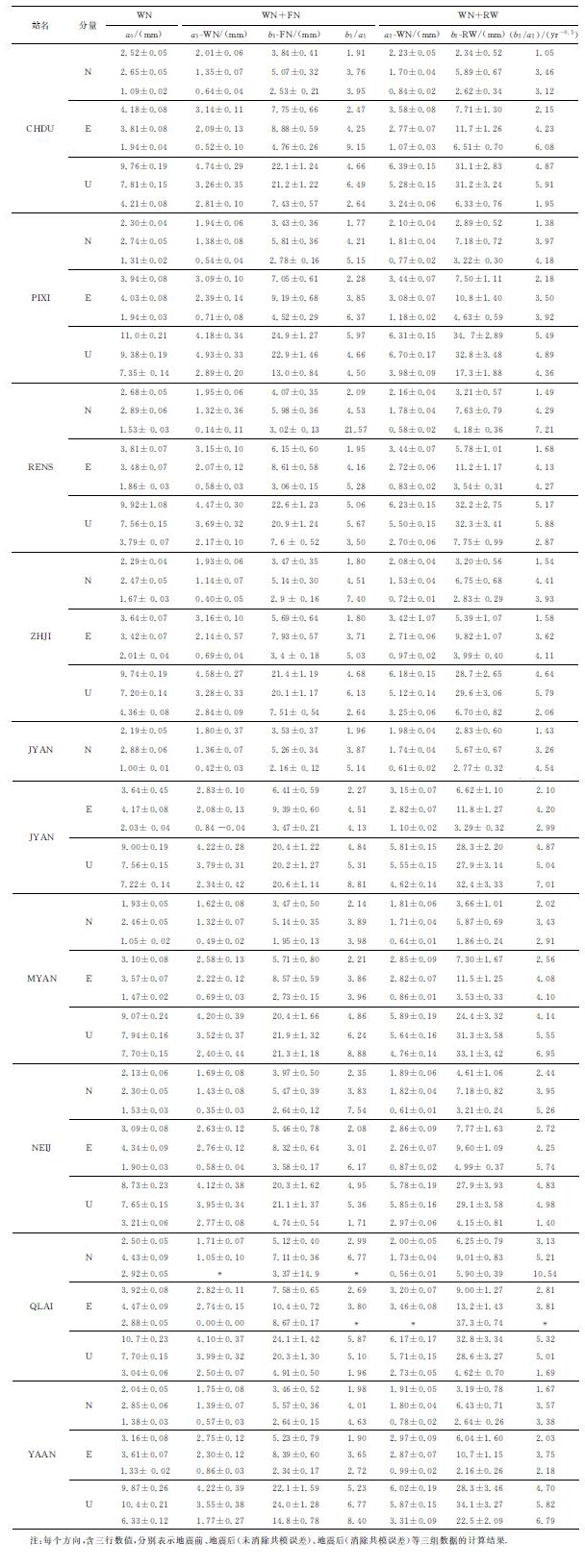
3.1 整数谱指数分析成果在进行MLE估计时, 将幂律噪声预定义为两种较为特殊的噪声形式, 一种为随机游走噪声(k=-2), 另一种为闪烁噪声(k=-1).该种方法中, 由于谱指数已知, 因此, 协方差矩阵的构造变得十分简单, 涉及的矩阵计算和迭代处理也明显减少, 计算效率可以显著提高.依据公式(1), 根据k值的选择不同, 可依次选择如下模型组合进行MLE估计, 分别为"白噪声(WN)"、"白噪声(WN)+闪烁噪声(FN)"、"白噪声(WN)+随机游走噪声(RW)", 同时需要将地震前、地震后坐标序列进行分别处理, 相应的噪声水平估值a, bk及其比率bk/a结果如表 1所示, 其中, 第一列为测站名, 第二列为方向分量(N为北向, E为东向, U为高向), 每个方向有三行数值, 分别表示地震前、地震后(未消除共模误差)、地震后(消除共模误差)等三组数据的计算结果, "±"表 95%置信区间的误差统计水平, *表示未能成功解算.
|
|
表 1 整数谱指数分析结果 Table 1 Results of in teger spectral index analysis |
可见, 不管是震前、震后, 还是消除共模误差后的震后数据, 其在N、E方向的噪声水平明显低于U方向(一般在3~4倍水平), 这与我们的传统认识是一致的; N方向的噪声水平普遍低于E方向(其相应的RMS值也略低于E方向), 这可能与N方向模糊度的解算成功率略高有关[8], 成功率越高, 则相应处理噪声越小; 同时, 通过比较各个站在同一时期的噪声分量, 可以发现, 不同测站在同一方向上的白噪声和幂律噪声水平基本一致, 排除因接收设备(9个站均使用了相同设备)和处理策略(9个站均使用GAMIT/GLOBK进行统一处理)可能引起的影响, 说明所有的站均受到相同的物理背景场的影响(如地壳环境、大气环境、电离层二次残差项等), 这也进一步说明噪声特征分析中进行共模处理消除的必要性, 但另一方面, 即便在消除共模误差后, 各个站的噪声分量仍然呈现一定的相关性, 这可能与台站均使用相同的接收设备和数据处理策略有关; 共模误差消除后, 白噪声和幂律噪声的噪声水平也显著降低(约2~3倍), 说明区域性物理背景场的存在是幂律噪声存在的主要原因之一.
值得注意的是, 与文献[2-3, 8]年的处理结果比较, 本次处理结果中, 白噪声和幂律噪声的估计精度都有显著提升, 尤其是幂律噪声, 其估计可靠性明显优于之前学者的处理结果, 说明当前GPS技术无论在设备接收处理能力还是在噪声控制等方面都得到了有效的提升.
比较地震前后的处理结果(暂不考虑共模误差消除后的数据)还可以发现, 对于白噪声模型而言, 地震前后其噪声水平并无显著改变, 而对于"白噪声+闪烁噪声"、"白噪声+随机游走噪声"而言, 其中的白噪声成分一般在震后会有微弱的减小, 而幂律噪声(尤其是随机游走噪声)一般有相对明显的增加, 这一点可通过地震前后, 幂律噪声与白噪声的比率b1/a1及b2/a2得到进一步确认, 这在一定程度上说明幂律噪声在震后GPS坐标序列中占据了更明显的主导地位, 这一结论将在本文的3.2节得到进一步证实.另外, 根据表 1也可发现, GPS数据处理中的传统假设, 即认为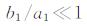
为了从统计角度判"白噪声+闪烁噪声"、"白噪声+随机游走噪声"两类模型是否比单纯的白噪声模型更适合于描述GPS噪声特性, 我们使用最大似然值对数比统计检验法[2, 14], 即Λ-检验:
Λ=exp(原假设最大似然对数值-备选假设最大似然对数值).
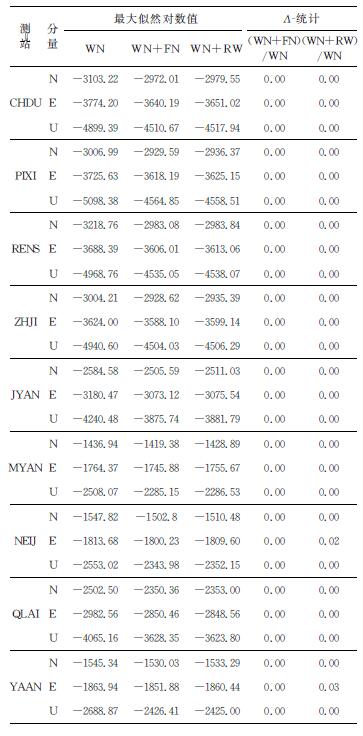
Λ值越趋近于1, 则原假设被接受的概率越大; 否则, 被拒绝的概率越大.表 2给出了以白噪声模型为原假设模型, "白噪声+闪烁噪声"、"白噪声+随机游走噪声"为备选假设模型时, 相应的Λ-检验结果, 可见, 所有的检验结果都基本趋近于0, 说明原假设正确的可能性几乎为0.另外, 从三种模型得到的最大似然值来看, 一般"白噪声+闪烁噪声"的最大似然值普遍高于其他两种模型(尽管其与"白噪声+随机游走噪声"的差异并不十分显著), 说明, "白噪声+闪烁噪声"模型可以最有效地描述本实验网络的综合噪声特性.
|
|
表 2 Λ-统计检验结果 Table 2 Results of Λ-statistic test |
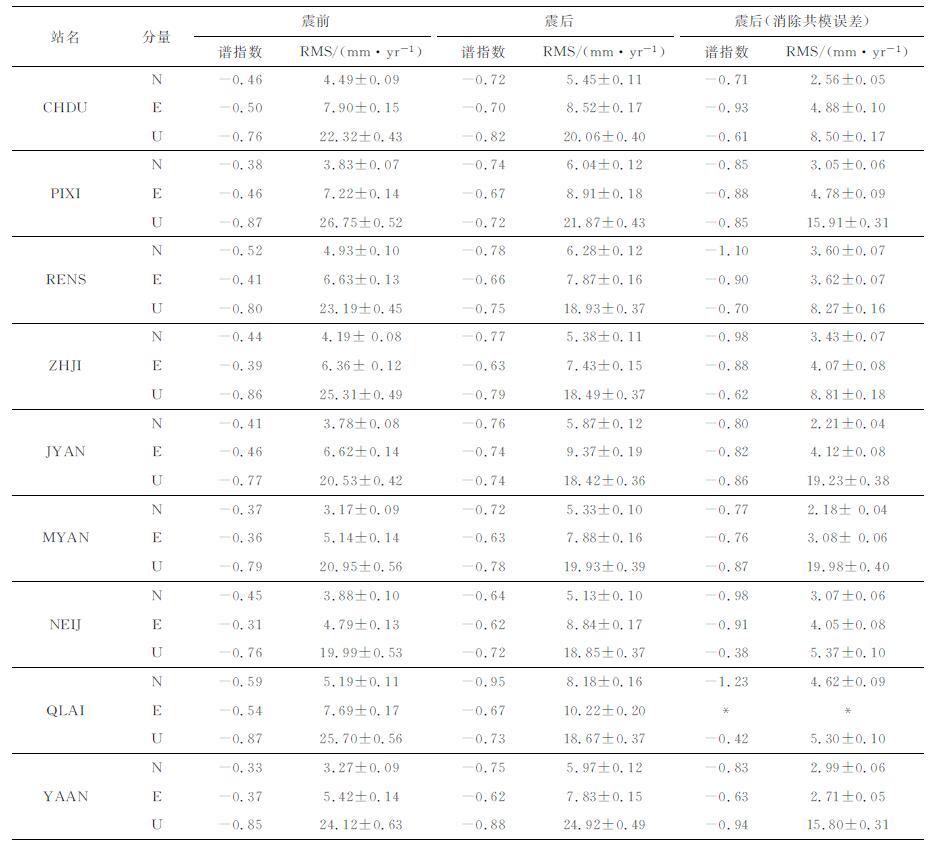
该分析方法不再对谱指数进行预定义, 而是将其作为未知量与年周期项、速率、白噪声等信息一同估计.任意谱指数分析方法由于不再进行任何人为约束(至少对于噪声分量而言), 因此, 计算出的真实谱指数信息将更有利于进行物理现象的解析和认识, 并可辅助我们有针对性地寻求噪声改进方案.使用任意谱指数分析方法, 对汶川地震前、地震后(未消除共模误差)、地震后(消除共模误差)等三组数据处理得到的各测站的谱指数估值及其误差水平统计结果见表 3.显见, 震后(无论是否消除了共模误差)各测站在NEU方向的谱指数估值都比震前出现了显著提高, 以水平方向为例, 震前各站谱指数均在(-0.31, -0.59)范围内变化, 统计均值约为-0.43, 而震后, 以未消除共模误差数据为例, 其谱指数均在(-0.62, -0.95)范围内变化, 统计均值约为-0.71, 参考表 1得出的结论, 可以确认, 震后观测序列的噪声分量中, 白噪声信息减弱, 幂律噪声占据了更明显的主导地位(更趋近于-1), 如果以"白噪声+闪烁噪声"作为候选模型组合, 则闪烁噪声(k=-1)的影响将处于绝对的主导地位.由此可见, 传统的幂律噪声分析方法中[1-3, 8], 简单地将地震前后的数据进行拼接并统一处理成单一的幂律谱指数信息的思路是不正确的, 同时, 简单地将拼接后的数据统一进行误差建模和统计精度分析也是不合理的.
|
|
表 3 任意谱指数分析结果 Table 3 Results of fractional spectral index analysis |
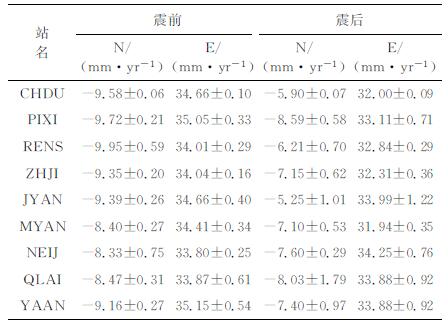
噪声分量发生显著变化这一结论也可从地震前后地表运动变化趋势中得到一些启示, 如表 4, 为参与解算测站使用地震前后约5年的数据得到的速度场变化信息, 可见, 震后各个测站在NE方向的运动速度都有一定程度的减缓, 而其统计噪声都有一定的增加, 地表运动趋于平缓则白噪声亦趋于平缓, 但背景场噪声增强则共模噪声增强, 幂律噪声增强.当然, 这一解释是否可作为诱发该现象的真正原因仍需更多的实验数据作进一步支撑.
|
|
表 4 汶川地震前后测站水平方向速度变化 Table 4 Velocity variation before and after Wenchuan earthquake inhorizontal direction |
本文以汶川地震为视角, 分析了地震事件对四川区域GPS坐标序列的噪声特征的影响, 并进行了初步的物理解释, 通过对地震前后幂律噪声分量、谱指数估值、Λ-统计检验等的对比分析, 得出地震事件对震后GPS坐标序列的噪声模型构建有着显著的影响, 传统幂律噪声分析中对地震事件的处理方法是不可取的.本文的实验结论及进一步工作总结如下:
(1)四川区域GPS坐标序列的噪声分量中含有明显的幂律噪声, "白噪声+闪烁噪声"可作为该区域噪声分量的最佳组合模型; 共模误差对GPS坐标序列噪声分量研究有显著影响, 合理消除共模误差可将噪声分量减弱3~4倍; 汶川地震事件导致GPS噪声分量谱指数从震前的-0.43增加至-0.71, 幂律噪声占据了明显的主导地位, 传统的幂律噪声分析方法中对地震事件的简单拼接并统一处理的方式不可取, 同时, 进行相关误差建模和精度分析时, 也应充分顾及该影响.
(2)篇幅限制, 本文还有许多细节问题未能一一展示并予以讨论, 如"白噪声+闪烁噪声"以及"白噪声+随机游走噪声"两类模型之间有何对比分析结果, 又如3.2节的谱指数估计中, 震前, NEU三个方向的的谱指数差异显著, 但震后, 三个方向的谱指数水平基本一致, 其本质原因是什么, 等等, 作者将在后续工作中对此做进一步讨论.
| [1] | Langbein J, Johnson H. Correlated errors in geodetic time series:Implications for time-dependent deformation. J. Geophys. Res. , 1997, 102(B1): 591-603. DOI:10.1029/96JB02945 |
| [2] | Zhang J, Bock Y, Johnson H, et al. Southern California permanent GPS geodetic array:Error analysis of daily position estimates and site velocities. J. Geophys. Res. , 1997, 102(B8): 18035-18055. DOI:10.1029/97JB01380 |
| [3] | Mao A L, Harrison C G A, Dixon T H. Noise in GPS coordinate time series. J. Geophys. Res. , 1999, 104(B2): 2797-2816. DOI:10.1029/1998JB900033 |
| [4] | Calais E. Continuous GPS measurements across the western Alps, 1994-1998. Geophys. J. Int. , 1999, 138(1): 221-230. DOI:10.1046/j.1365-246x.1999.00862.x |
| [5] | Bock Y, Nikolaidis R M, de Jongp P J, et al. Instantaneous geodetic positioning at medium distances with the Golbal Positioning System. J. Geophys. Res. , 2000, 105(B12): 28223-28253. DOI:10.1029/2000JB900268 |
| [6] | Johnson H, Agnew D C. Monument motion and measurements of crustal velocities. Geophys. Res. Lett. , 1995, 22(21): 2905-2908. DOI:10.1029/95GL02661 |
| [7] | Johnson H, Agnew D C. Correlated noise in the geodetic time series, U.S.. Geol. Surv. Final Tech. Rep. , 2000. |
| [8] | Williams S D P, Bock Y, Fang P, et al. Error analysis of continuous GPS position time series. J. Geophys. Res. , 2004. DOI:10.1029/2003JB002741 |
| [9] | Williams S D P. The effect of coloured noise on the uncertainties of rates estimated from geodetic time series. J. Geodesy , 2003, 76(9-10): 483-494. DOI:10.1007/s00190-002-0283-4 |
| [10] | Press W H, Teukolsky S A, Vetterling W T, et al. Numerical Recipes in C. (2nd ed). New York: Cambridge University Press, 1992 : 818 . |
| [11] | Williams S D P. Create and Analyse Time Series:CATS software V3.1.1. GPS Solutions, 2005. http://sddnserror2.wo.com.cn:8080/?HOST=tianyf.dyndns.org&R=/software/cats/cats_v312.pdf& |
| [12] | Wdowinski S, Bock Y, Zhang J, et al. Southern California permanent GPS geodetic array:Spatial filtering of daily positions for estimating coseismic and postseismic displacements induced by the 1992 Landers earthquake. J. Geophys. Res. , 1997, 102(B8): 18057-18070. DOI:10.1029/97JB01378 |
| [13] | Bock Y, Wdowinski S, Fang P, et al. Southern California permanent GPS geodetic array:Continuous measurements of crustal deformation between the 1992 Landers and 1994 Northridge earthquakes. J. Geophys. Res. , 1997, 108(B8): 18013-18033. |
| [14] | Kedall S M, Stuart A. The Advanced Theory of Statistics, vol.2, Inference and Relationship. London:Charles Griffin, 1979:240-274. |
 2013, Vol. 56
2013, Vol. 56