中高层大气(80~300km高度)是整个大气层的暴风层,是航天发射的一个危险区域.中高层大气风场是该层大气的基本参量之一,是重要的空间环境参量.其不仅对中高层大气、上下层之间能量的传输起着重要作用,还对航天器的运行轨道和安全有很大的影响.因此,风场测量不仅可以为大气模式的建立提供重要基础数据,为大气动力学与光化学耦合过程研究提供重要的探测资料,还可以为卫星等航天设备的安全运行和寿命保障等提供可靠的参考资料.
目前,针对中高层大气风场的探测方式主要分为两类,一是地基探测,二是星载遥感探测,它们利用干涉光谱技术不间断地观测大气中气辉或极光谱线的多普勒效应进行大气风速反演.目前,该技术采用的干涉光谱仪主要分为两类:Fabry-Perot干涉仪和Michelson干涉仪.Fabry-Perot干涉仪通过平行标准板(F-P腔)形成多光束等倾干涉,然后基于傅里叶变换的思想,通过干涉条纹的变化反演得到大气风场等信息;Michelson干涉仪则通过光学运动部件连续四次改变同一探测像元光程差得到四组不同的干涉强度值,并将其组成方程组,计算得到风场等参数(四强度法).相对于Michelson干涉仪,Fabry-Perot干涉仪具有高灵敏度、高光谱分辨率以及结构简单等优点,被广泛地应用到中高层大气风场的探测中.此外,FPI干涉成像的光路上没有移动部件,属于静态干涉成像光谱技术,稳定性较高,抗震干扰能力较强,具有较高的能量利用率和探测灵敏度[1].
国际上,基于FPI的中高层大气风场探测研究始于20世纪60年代[2-3].迄今为止,美国、英国和日本等国家已在多个地方布置了多台地面FPI,用于中高层大气的风场测量.而星载风场测量FPI数量相对较少:1982年DE-2卫星上搭载的Fabry-Perot干涉仪(DE-FPI)首次实现了高层大气风场的星载测量[4].1991年9月,搭载在UARS卫星上的FPI干涉仪成功发射,它采用三个串联的平行标准具进行太阳散射光的吸收线和气辉发射线观测,从而实现大气中间层和低热层的风速、温度及体发射率等信息的测量[5-7].2001年,搭载在TIMED卫星上的TIDI多普勒成像仪采用单FPI对中高层大气的水平矢量风和温度进行探测,完成了中高层大气日、夜间风场的快速测量,并实现了大气温度和微量成分的同时测量,其采用的气辉观测谱线主要有原子氧绿线(557.7nm)、原子氧红线(630.0nm)和氧分子O2(0-0)带[8-10]等.
在国内,大气风场探测研究虽已有几十年的历史,但基本上都在近地表高度进行探测,而关于中高层大气风场探测的研究近些年才刚刚起步.在国家重大课题子午工程中,中国科学院空间中心利用国外引进的地基FPI[11-12]和流星雷达[12-13]在国家天文台兴隆园区对中高层大气风场进行了连续观测,获得的反演结果与HWM93模式结果具有较好的一致性,实现了我国中高层大气风场的业务化地基风场探测.此外,对于FPI大气风场探测数据处理,中国科学院空间中心[1, 14]、中国科学院西安光机所[15-16]和武汉大学[17-18]等单位进行了相关研究.武汉大学[17-19]等利用KUBOTA提出的闭合式干涉环圆心坐标对称迭代法确定圆心,进而进行圆周积分和高斯拟合求得半径,以实现大气风速的模拟反演.西安光机所[16]针对FPI闭合式干涉环圆心和半径的确定进行了研究,其采用最小二乘法进行圆拟合,同时得到干涉环圆心和半径.空间中心[1, 20]通过VC编程实现了FPI干涉条纹细化的自动化处理,采用重复剥离二值图像边界元素骨架提取法,对非闭合式干涉环条纹进行了细化处理,但对于干涉环圆心和半径的计算方法需要进一步研究.
目前,基于FPI的中高层大气风场数据处理研究的对象主要为闭合式干涉环,但为了节约资源,减少探测成本,FPI干涉仪可采用非闭合式干涉成像.本文则通过干涉条纹峰值拟合(高斯拟合)与圆心拟合(圆拟合)相结合的迭代方法实现了非闭合式干涉环圆心和半径的确定,并将其用于FPI的仿真数据处理进而反演得到大气风速.
2 Fabry-Perot大气风速反演基本原理Fabry-Perot干涉仪(FPI)通过观测中高层大气气辉或极光得到干涉图样,利用干涉条纹的变化得到多普勒频移,进而反演得到风速.FPI的核心部件为两块镀膜(高反射率膜)平行标准板构成的F-P腔,入射光在腔内经过多次反射后透射出来可形成等倾干涉,经过聚焦透镜在CCD探测器上成像为一组同心干涉环.
设T为标准具强度透过率,R为强度反射率,则FPI的透射函数为

|
(1) |
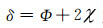
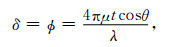
|
(2) |
式(2)中,t为FPI标准板间距,μ为板间介质的折射率,λ为入射光波长,θ为FPI标准具腔内反射角.当θ非常接近于零时,则θ≈tanθ=r/f,将式(2)进行泰勒级数展开得:
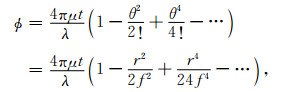
|
(3) |
r为条纹峰值到干涉环圆心的距离,即干涉环半径,f为成像系统焦距.由于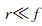
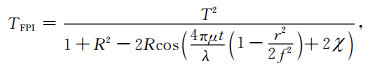
|
(4) |
忽略χ的情况下,当透射光强度最大即处于条纹峰值时(m为整数)
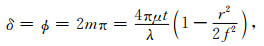
|
(5) |
由式(5)得:
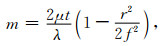
|
(6) |
当入射波长受风速影响产生多普勒波长位移Δλ时,条纹峰值到条纹中心的距离变为rλ+Δλ,则式(6)转化为:
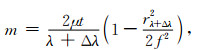
|
(7) |
由多普勒频移可知,风速与波长之间存在如下关系:

|
(8) |
c为光速.将式(8)代入(7)中,并将式(6)与(7)右侧相等,得风速表达式为
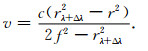
|
(9) |
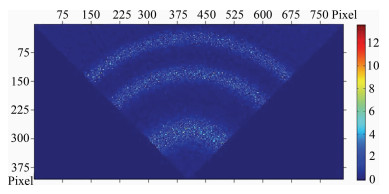
FPI成像在CCD探测器上的干涉环图样主要分为两种,一是闭合式干涉环(图 1),二是非闭合式干涉环(图 2).闭合式干涉环可通过圆环坐标对称迭代的方法来实现圆心确定[22-23],进而对各干涉条纹峰值附近强度进行高斯拟合得到圆环半径[24-25].实测中FPI多采用部分干涉环成像,即非闭合式干涉环.其圆心可采用圆环上多个峰值采样点再分别两两连线作中垂线的方法[20]来确定,即在圆环上等间隔取多个峰值样点,分别作两两样点连线的法线,两两法线交点分布的中心即为干涉环的圆心.上述方法中,峰值样点的选取随机性较大,峰值样点选取精度有限,直接影响了干涉环圆心的确定精度,只适合用于干涉条纹细化后的圆心确定.本文针对非闭合式干涉环(以扇形为例)提出干涉圆环拟合迭代法,将峰值高斯拟合与圆拟合相结合,同时得到干涉环的圆心和半径.

|
图 1 FPI闭合式干涉图 Fig. 1 FPI closed interference fringes |
|
图 2 FPI非闭合式干涉图(扇形) Fig. 2 FPI non-closed interference fringes (fan-shaped) |
由式(9)可知,大气风速的反演需要精确确定FPI干涉环条纹的圆心和半径.圆心和半径确定的主要思路为:
(1)数据预处理.对干涉图像进行噪声去除预处理,包括均值滤波和自适应滤波.
(2)圆心和半径的确定.初步确定圆心,利用高斯函数拟合确定干涉条纹峰值位置,利用峰值位置进行圆拟合,得到新的圆环圆心和半径,以新圆心值为中心重复上述过程,直到圆心坐标值收敛.
(3)获得准确的圆环圆心和半径.
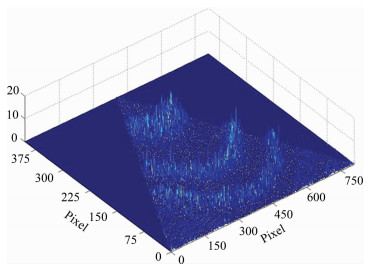
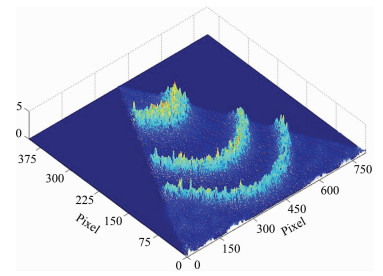
3.1 数据预处理由于气辉的辐射强度一般较弱,实际测量的FPI干涉图像对比度较低,极易受到噪声的影响和干扰,表现为局部光强发生突变或者出现奇异值.这些噪声除来自宇宙射线的干扰外,还来自杂散光的影响,包括仪器本身和周围环境的扰动,它们会直接影响圆心和条纹峰值位置的确定.因此,进行风速反演前,首先需要对FPI干涉图进行噪声去除预处理:包括均值滤波[26]和自适应滤波[27].图 3为Zemax软件模拟仿真FPI系统得到的处理前干涉光强分布图(三维),图中干涉光强分布参差不齐,噪声明显;经过噪声处理后,干涉光强分布如图 4所示,图中光强分布相对比较平滑,干涉环状分布明显,噪声得到抑制.
|
图 3 FPI去噪声处理前干涉光强分布图 Fig. 3 Interference strength distribution of FPI before denoising processing |
|
图 4 FPI去噪声处理后干涉光强分布图 Fig. 4 Interference strength distribution of FPI after denoising processing |
以CCD为平面建立XY坐标系,非闭合式干涉环圆心和半径的确定步骤如下:
(1)初步估计干涉环圆心坐标(Cx,Cy).
(2)以干涉环圆心初始坐标为中心建立n条等角度间隔线,得到n条干涉环横剖线(图 5).
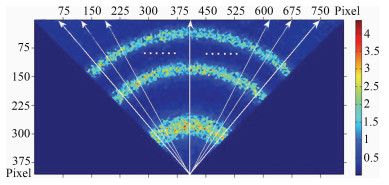
|
图 5 干涉环横剖射线示意图 Fig. 5 Cross sections of FPI interference fringes |
(3)提取每级干涉条纹有效信息,由于干涉条纹在峰值附近的强度符合高斯分布[28-31],因此分别沿n条射线方向对干涉条纹峰值附近强度进行高斯函数拟合(函数: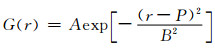
(4)根据干涉环n个峰值位置坐标,利用最小二乘法进行圆拟合,得到新的干涉环圆心和半径.
(5)将所得新圆心与原圆心值进行比较,并设置迭代停止条件:圆心横坐标Cx和纵坐标Cy变化分别收敛在0.5个像素以内,满足此条件则停止迭代运算,否则重复上述计算步骤,直到迭代收敛,得到准确的圆环圆心和半径.
4 风速反演仿真模拟与结果分析利用光学设计软件Zemax的非序列模式模拟FPI系统,相关仿真参数设置如表 1所示.
|
|
表 1 风速反演仿真设计参数 Table 1 FPI constants and parameters used in the simulation |
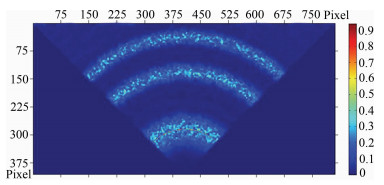
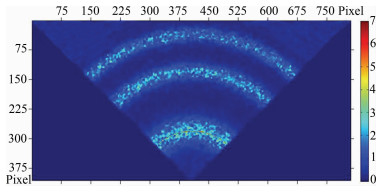
仿真系统中,CCD探测器面积大小为13.3mm× 13.3mm,像元个数为1024×1024,单像元面积大小为13μm×13μm (实际观测中CCD使用像元大小).由于原子氧红线气辉在电离层F层高度上具有相对较强的辐射强度及其在中高层大气中普遍存在,被广泛应用于该区域的风速反演,因此本次仿真选用零风速原子氧红线波长630.0000nm作为参考波段,仿真得到的(经过去噪声处理)干涉强度分布如图 6所示.由于中高层大气风速较大,一般为每秒几十到几百米[17, 32],因此本次仿真选取风速为~100m/s所对应的原子氧红线波长629.99979nm进行仿真,得到的干涉强度分布(经过去噪声处理)如图 7所示.为了验证3.2节中圆心和半径确定方法对低风速反演的有效性,本次仿真还选用理论风速~10m/s对应的波长629.999979nm进行仿真,干涉强度分布(经过去噪声处理)如图 8所示.
|
图 6 波长为630.0000nm干涉强度分布及圆拟合 Fig. 6 Circle fitting and interference strength distribution at λ=630.0nm |
|
图 7 波长为629.99979nm干涉强度分布及圆拟合 Fig. 7 Circle fitting and interference strength distribution at λ=629.99979nm |

|
图 8 波长为629.999979nm干涉强度分布及圆拟合 Fig. 8 Circle fitting and interference strength distribution at λ=629.999979nm |
采用第3节中所述数据处理方法进行圆环中心和半径迭代计算.得到波长λ0=630.0nm仿真干涉环圆心为:(413.3283,408.5913),干涉环半径像元个数为127.5308(图 6),对应半径长度r为1.6579mm;波长λ1=629.99979nm干涉环圆心为:(413.3571,409.3311),干涉环半径像元个数为132.8231(图 7),对应半径长度rλ+Δλ1为1.7267 mm.根据多普勒频移,将λ0和λ1代入式(8),得到理论风速值为99.9307m/s;将rλ+Δλ1代入式(9)得到风速反演值为96.9537m/s,反演绝对误差为-2.977m/s,相对误差为-2.98%.波长λ2=629.999979nm仿真干涉环圆心为:(411.9925,412.0979),干涉环半径像元个数为127.9429 (图 8),对应半径长度rλ+Δλ2为1.6633mm.将λ0和λ2代入式(8),得到理论风速值为9.9931m/s;将r和rλ+Δλ2代入式(9)得到风速反演值为7.5282m/s,反演绝对误差为-2.465m/s,反演相对误差为-24.67%.
两次仿真得到的风速反演绝对误差分别为-2.977m/s和-2.465m/s,误差绝对值小于3m/s,达到了中高层大气风速反演误差5 m/s的精度要求[4].高风速反演相对误差为-2.98%,低风速反演相对误差为-24.67%,由于中高层大气风速一般为每秒几十到几百米,因此本文提出的圆心和半径确定算法满足中高层大气风速反演精度的要求.而低风速的反演相对误差较大主要是由CCD像元尺寸造成的.由式(9)及表 1仿真参数可知,圆环半径确定误差为1μm时引起的风速反演误差可达2.34m/s,而本次仿真CCD像元尺寸为13μm (实际观测中CCD使用像元大小),远远大于半径确定所需尺寸,因此像元尺寸是圆环圆心、半径确定以及风速反演误差的重要因素.在今后的工作中,将结合像元细分方法,对圆心和半径确定算法进行进一步研究和验证.
5 结论本文基于Fabry-Perot干涉仪非闭合式干涉环提出了一种提取干涉环圆心和半径的新方法,其既结合了干涉环的强度分布信息(高斯拟合),又运用了圆环的空间分布信息(圆拟合),有利于提高风速的反演精度.主要反演思路:首先,对干涉图像进行噪声去除预处理,然后初步确定圆心,并以其为中心作n条射线,分别沿射线对干涉条纹强度分布进行高斯拟合以确定干涉条纹n个峰值位置,利用这些峰值位置进行圆拟合,得到新的圆心和半径,将所得圆心坐标与原圆心坐标进行比较,收敛则停止运算,否则重复上述步骤,直到圆心坐标收敛.利用该方法对FPI仿真数据进行处理进而进行风速反演,反演绝对误差在3m/s以内,满足中高层大气风速反演精度的要求,初步验证了该方法对圆心和半径确定的可行性.但为了实现低风速高精度的反演,更精确的反演中高层大气风速,下一步将CCD像元细分处理与本文提出的迭代算法相结合,以细化像元尺寸,进一步对低风速反演误差进行分析研究.
| [1] | 韩威华, 王咏梅, 吕建工, 等. 中高层大气风场星载FPI干涉条纹的处理. 科学技术与工程 , 2010, 10(10): 2420–2423. Han W H, Wang Y M, Lü J G, et al. Auto-processing of middle and upper atmosphere wind FPI interference fringe pattern. Science Technology and Engineering (in Chinese) , 2010, 10(10): 2420-2423. |
| [2] | Killen T L, Kennedy B C, Hays P B, et al. Image plane detector for the dynamics explorer Fabry-Perot interferometer. Appl. Opt. , 1983, 22(22): 3503-3513. DOI:10.1364/AO.22.003503 |
| [3] | Killeen T L, Hays P B. Doppler line profile analysis for a multichannel Fabry-Perot interferometer. Appl. Opt. , 1984, 23(4): 612-620. DOI:10.1364/AO.23.000612 |
| [4] | Hays P B, Killeen T L, Kennedy B C. The Fabry-Perot interferometer on dynamics explorer. Space Sci. Instrum. , 1981, 5: 395-416. |
| [5] | Skinner W R, Hays P B, Abreu V J. High resolution Doppler imager. Ann Arbor: International Geoscience and Remote Sensing Symposium, 1987: 673-676. |
| [6] | Abreu V J, Hays P B, Skinner W R. The high resolution Doppler imager. Opt. Photon. News , 1991, 2(10): 28-30. DOI:10.1364/OPN.2.10.000028 |
| [7] | Hays P B, Abreu V J, Dobbs M E, et al. The high-resolution Doppler imager on the upper atmosphere research satellite. Journal of Geophysical Research , 1993, 98(D6): 10713-10723. DOI:10.1029/93JD00409 |
| [8] | Killen T L, Skinnerm W R, Johnson R M, et al. TIMED Doppler interferometer (TIDI). SPIE , 1999, 3756: 289-301. |
| [9] | Skinner W R, Niciejewski R J, Killen T L, et al. Operational performance of the TIMED Doppler interferometer (TIDI). SPIE , 2003, 5157: 47-57. |
| [10] | Killeen T L, Wu Q, Solomon S C, et al. TIMED Doppler Interferometer: Overview and recent results. J. Geophys. Res. , 2006, 111: A10S01. DOI:10.1029/2005JA011484 |
| [11] | 袁伟, 徐寄遥, 马瑞平, 等. 我国光学干涉仪对中高层大气风场的首次观测. 科学通报 , 2010, 55(35): 4046–4051. Yuan W, Xu J Y, Ma R P, et al. First observation of mesospheric and thermospheric winds by a Fabry-Perot interferometer in China. Chinese Science Bulletin (in Chinese) , 2010, 55(35): 4046-4051. DOI:10.1007/s11434-010-4192-2 |
| [12] | Jiang G Y, Xu J Y, Yuan W, et al. A comparison of mesospheric winds measured by FPI and meteor radar located at 40N. Sci. China Tech. Sci. , 2012, 55(5): 1245-1250. DOI:10.1007/s11431-012-4773-1 |
| [13] | 姜国英, 徐寄遥, 史建魁, 等. 我国海南上空中高层大气潮汐风场的首次观测分析. 科学通报 , 2010, 55(11): 1059–1066. Jiang G Y, Xu J Y, Shi J K, et al. The first observation of the atmospheric tides in the mesosphere and lower thermosphere over Hainan, China. Chinese Science Bulletin (in Chinese) , 2010, 55(11): 1059-1066. DOI:10.1007/s11434-010-0084-8 |
| [14] | 王咏梅, 付利平, 杜述松, 等. 中高层大气风场和温度场星载探测技术研究进展. 空间科学学报 , 2009, 29(1): 1–5. Wang Y M, Fu L P, Du S S, et al. Development for detecting upper atmospheric wind and temperature from satellite. Chin. J. Space Sci (in Chinese) , 2009, 29(1): 1-5. |
| [15] | 张淳民, 相里斌, 赵葆常. 用Fabry-Perot干涉仪测量上层大气风场的速度和温度. 西安交通大学学报 , 2000, 34(4): 97–99. Zhang C M, Xiang L B, Zhao B C. Velocity and temperature measurement of upper atmosphere wind field using Fabry-Perot interferometer. Journal of Xi'an Jiaotong University (in Chinese) , 2000, 34(4): 97-99. |
| [16] | 汪丽, 周毅, 华灯鑫, 等. 基于法布里-珀罗干涉仪的大气风场及温度场探测理论研究及仿真. 光学学报 , 2011, 31(10): 1001001-1–1001001-6. Wang L, Zhou Y, Hua D X, et al. Theoretical research and simulation of the atmospheric wind field and temperature based on the Fabry-Perot interferometer. Acta Optica Sinica (in Chinese) , 2011, 31(10): 1001001-1-1001001-6. |
| [17] | 赵正启, 周小珊, 艾勇. 扫描式法布里--珀罗干涉仪测量高空大气风速. 应用光学 , 2006, 27(6): 558–562. Zhao Z Q, Zhou X S, Ai Y. Wind-velocity detection in upper atmosphere with scanning Fabry-Perot interferometer. Journal of Applied Optics (in Chinese) , 2006, 27(6): 558-562. |
| [18] | 李浩, 张燕革. 模拟大气风场及其数据处理技术的研究. 应用光学 , 2009, 30(2): 285–290. Li H, Zhang Y G. Simulation and analysis of thermospheric wind velocity. Journal of Applied Optics (in Chinese) , 2009, 30(2): 285-290. |
| [19] | 鄂非, 高秋燕, 艾勇. 一种新的Fabry-Perot干涉条纹处理方法. 光学技术 , 2009, 35(4): 499–501. E F, Gao Q Y, Ai Y. A new method of processing the Fabry-Perot interference fringes. Optical Technique (in Chinese) , 2009, 35(4): 499-501. |
| [20] | 韩威华, 吕建工, 王咏梅, 等. Fabry-Perot测风干涉仪数据处理. 空间科学学报 , 2011, 31(6): 784–788. Han W H, Lü J G, Wang Y M, et al. Image data processing of Spaceborne Fabry-Perot interferometer prototype. Chin. J. Space Sci. (in Chinese) , 2011, 31(6): 784-788. |
| [21] | Wilksch P A. Instrument function of the Fabry-Perot spectrometer. Appl. Opt. , 1985, 24(10): 1502-1511. DOI:10.1364/AO.24.001502 |
| [22] | Kubota M. A study on middle-scale variations of thermospheric neutral winds associated with auroral activity over Syowa station, Antarctica. Japan: Tohoku University, 1996. |
| [23] | Shiokawa K, Kadota T, Otsuka Y, et al. A two-channel Fabry-Perot interferometer with thermoelectric-cooled CCD detectors for neutral wind measurement in the upper atmosphere. Earth, Planets Space , 2003, 55: 271-275. DOI:10.1186/BF03351759 |
| [24] | Dyson P L, Davies T P, Parkinson T P, et al. Thermospheric neutral winds at southern mid-latitudes: A comparison of optical and ionosonde hmF2 methods. J. Geophys. Res. , 1997, 102(A12): 27189-27196. DOI:10.1029/97JA02138 |
| [25] | Biondi M A, Sazykin S Y, Fejer B G, et al. Equatorial and low latitude thermospheric winds: measured quiet time variations with season and solar flux from 1980 to 1990. J. Geophys. Res. , 1999, 104(A8): 17091-17106. DOI:10.1029/1999JA900174 |
| [26] | Lim J S. Two-Dimensional Signal and Image Processing. Englewood Cliffs: Prentice Hall, 1990: 469-476. |
| [27] | Lim J S. Two-Dimensional Signal and Image Processing. Englewood Cliffs:, Prentice Hall, 1990: 548. |
| [28] | Shepherd G G, Guit W A, Miller D W, et al. WAMDII, wide-angle Michelson Doppler imaging interferometer for space lab. Appl. Opt. , 1985, 24(11): 1571-1583. DOI:10.1364/AO.24.001571 |
| [29] | Hays P B. Circle to line interferometer optical system. Appl. Opt. , 1990, 29(10): 1482-1489. DOI:10.1364/AO.29.001482 |
| [30] | Killeen T L, Roble R G. Thermosphere dynamics: Contributions from the first 5 years of the Dynamics Explorer program. Rev. Geophys. , 1988, 26(2): 329-367. DOI:10.1029/RG026i002p00329 |
| [31] | Shiokawa K, Kadota T, Mitsumu K E, et al. Three-channel imaging Fabry-Perot interferometer for measurement of mid-latitude airglow. Appl. Opt. , 2001, 40(24): 4286-4296. DOI:10.1364/AO.40.004286 |
 2013, Vol. 56
2013, Vol. 56


