电离层是近地卫星运行的主要场所, 也是空间天气对人类活动影响的重要区域.由太阳风暴引起的电离层扰动会影响GPS定位系统的精度、无线电通信的质量和电力传输的安全.电离层也是导弹、低轨卫星和空间站的主要运行场所, 其环境状况将直接影响运行其中的飞行器寿命、功能实现以及宇航员的健康安全等[1].由于电离层扰动时常发生, 变化快, 动态范围大, 因此有效地监测电离层状态, 尤其是电子密度剖面(Electron Density Profile, EDP)和总电子含量(Total Electron Content, TEC)成为国内外研究的重点.
传统的探测方法, 如电离层测高仪只能探测底部电离层, 非相干散射雷达能探测800km以下电子密度剖面, 提供电离层多个参量信息, 但其造价和运行成本非常昂贵, 且二者都受到站点分布、探测时间和频率的限制, 不能满足全球高分辨力探测的需求.自20世纪70年代以来, 美国NASA开始发展用于电离层极光和气辉观测的远紫外光谱成像遥感技术, 因其良好的时空分辨力而备受该领域的研究者的青睐.过去, 针对如何由远紫外成像光谱仪观测数据反演得到电离层参量, 国内外学者进行了大量研究[2-7].在远紫外气辉遥感EDP的反演问题上, 国外的研究大多是在电子密度剖面满足Chapman函数的假设下进行的, 这使得到的峰值电子密度与峰值高度误差较大; 而国内对这一问题的研究尚未涉足.研究远紫外光谱遥感反演EDP的方法, 不但能够丰富电离层监测的数据来源, 也将为未来我国同类光谱数据快速转化为数据产品服务.
本研究基于搭载TIMED飞船的全球紫外成像仪(Global Ultraviolet Imager, GUVI)探测得到的氧原子135.6nm夜气辉光谱数据, 利用正则化和牛顿迭代法相结合的方法计算得到了自由形式的电离层电子密度剖面, 之后将其与电离层电子密度的Chapman表达式相结合, 得到Chapman拟合结果.
2 数据来源及观测模型 2.1 数据来源GUVI[8]于2001年12月搭载TIMED卫星进入近极地太阳同步轨道, 轨道周期为97.8 min, 轨道高度625km, 倾角为74.1°.本研究利用GUVI临边观测得到的氧原子135.6nm夜气辉光谱数据反演得到电子密度剖面, 其体辐射速率可表示为
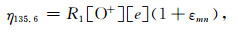
|
(1) |
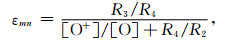
|
(2) |
式中, εmn表征了中和作用在氧原子135.6nm夜气辉中的贡献, R1=7.3×10-13、R2=10-7、R3=1.3× 10-15、R4=1.4×10-10分别是相关反应的反应速率, 单位为cm3/s.
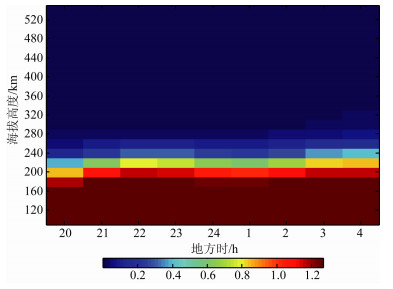
如图 1所示, 是利用大气模式NRL MSISE-00和国际参考电离层模型IRI-2011计算得到的1992年3月21日(30°N, 0°E)处中和作用的贡献εmn.氧原子135.6nm夜气辉中, 约75%来源于辐射复合反应, 25%来源于中和作用[9-11], 且由图可知中和作用的贡献仅在250km以下才变得显著.因此, 在计算中可以忽略中和作用的影响, 认为氧原子135.6nm夜气辉光谱数据仅由辐射复合反应产生.另外, 由于O+是F层等离子体中最主要的成分(含量在99%以上), 且F层呈整体电中性, 在本研究中认为
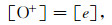
|
(3) |
|
图 1 εmn随海拔高度和当地时间的变化 Fig. 1 εmn variation with altitude and local time |
因此, 体辐射速率η可近似表示成
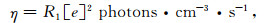
|
(4) |
其中, [e]为电子密度.
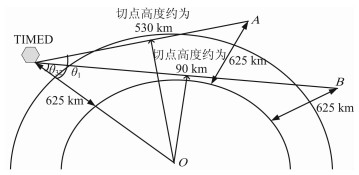
2.2 观测模型在TIMED飞船沿轨飞行的同时, GUVI扫描成像系统在穿轨方向以0.4°的步长扫描与星下点成67.2°到80°的临边区域, 在一次扫描中获得32× 14个像元值.如图 2所示, 从仪器的成像方式来看, 每个像元值是观测方向上从电离层切点到GUVI所在位置的辐射之和.为了去除随机噪声带来的影响, 对沿轨方向的14个像元求平均赋值于中心像元.于是, 一次扫描的32个像元与32个切点高度相关.若将电离层看作是球对称分层结构, 则海拔高度为90~530km的电离层均匀分成23层, 可建立离散形式的观测模型
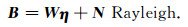
|
(5) |
|
图 2 GUVI临边观测结构示意图 Fig. 2 Geometrical chart of GUVI limb observing |
对一次扫描来说, 观测向量B为32×1的列向量; 权重矩阵W为32×23, 其每行中各元素为各层辐射在观测值中所占比例; 体辐射速率η为23×1的列向量; N为附加的噪声项.
2.2.1 噪声分析光子散粒噪声是GUVI探测数据噪声的主要来源, 本研究仅考虑光子散粒噪声的影响.光子散粒噪声是与入射光子数的随机变化有关的噪声, 在给定时间内入射光子数服从泊松分布, 光子散粒噪声σshot可由信号电子数Se(以电子数计)的均方根值表示为
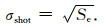
|
(6) |
GUVI灵敏度为0.5 counts/s/Rayleigh/pixel, 像元积分时间为0.064s, 考虑本模型采取了14像元合并的方式, 则模型中附加噪声项可表示为
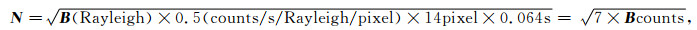
|
(7) |
其中, B取式(5)观测向量中的观测值.
2.2.2 权重矩阵前面, 在电离层为球对称分层结构这一假设下建立了观测模型.权重矩阵每行中各个元素仅与各层到探测器的距离有关[12].于是, 在观测模型中, 可认为所有位置的权重矩阵是相同的.权重矩阵的特性直接影响反演结果的准确性, 本研究计算得到法矩阵WTW的条件数为3469.一般认为条件数小于100时为良态; 条件数在100到1000之间时为中等程度的病态; 条件数超过1000时存在严重的病态[13].可见本研究中电子密度剖面反演问题存在严重病态.
综上, 由建立的临边观测模型得出电离层电子密度剖面反演问题转化为如下的最小二乘最优问题:
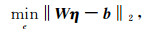
|
(8) |
其中, b为观测值与噪声值之差.然而, 由于观测模型中权重矩阵W的病态性, 往往使得由普通的最小二乘法求得的估计值与真值之间存在较大差别, 因此, 本研究采用正则化方法增加约束项来求解上述问题.
3 反演方法针对上述病态问题, Tikhonov提出了正则化方法.正则化方法的关键是增加全部或部分参数(或参数改正数)加权平方和极小的条件来增加约束, 克服不适定性, 使解唯一且稳定, 即用相邻的适定问题的解去逼近原问题的解.于是, 为使式(8)有唯一稳定的解, 构造准则函数
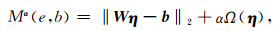
|
(9) |
使式(9)最小化的参数η即为所建立的观测模型的正则化解.其中, Ω(η)称为稳定泛函, α是正则化参数(或称为平滑因子、岭参数).在实际计算中, 稳定泛函Ω(η)可取不同的形式, 这里取Ω(η)=ηTHη, 其中正则化矩阵H=D2TD2, D2通常可取单位矩阵、拉普拉斯算子的一阶和二阶差分矩阵, 这里取二阶差分形式的拉普拉斯算子, 即
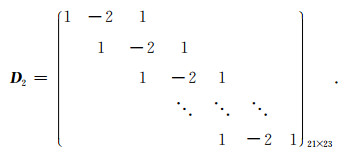
|
(10) |
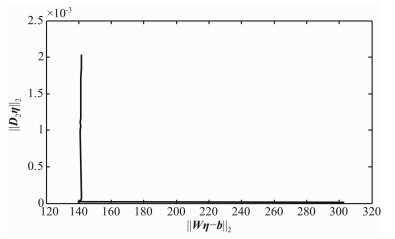
目前, 确定正则化参数的常用方法有L-曲线法和GCV法(Generalized Cross-Validation)[14], 本研究采用L-曲线法确定正则化参数.由于‖Wη -b‖2和‖D2η‖2都是正则化参数α的函数, 选择不同的α值, 以‖Wη -b‖2为横坐标, ‖D2η‖2为纵坐标, 经过曲线拟合得到L-曲线, 如图 3所示.
|
图 3 L-曲线 Fig. 3 L-curve |
由于牛顿迭代法具有快速收敛的特点, 本研究采用其寻找未知参数η的最优解.迭代公式[15]如下
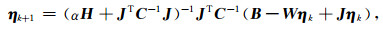
|
(11) |
其中, J为Wη在ηk处的雅克比矩阵取值, C为观测值噪声的协方差矩阵.迭代终止条件为
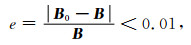
|
(12) |
其中, B0为辐射估计值.
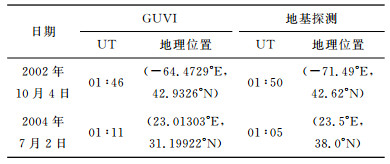
4 反演结果及分析 4.1 与地基探测数据的对比利用正则化和牛顿迭代相结合的方法, 选取存在近同步传统观测的GUVI临边观测氧原子135.6nm夜气辉辐射数据, 反演得到2002年10月4日和2004年7月2日自由形式的电离层电子密度剖面, 详细参数列于表 1中, 将地基近同步观测数据及全解析性电离层模型FAIM[16]得到的电子密度剖面与本研究结果绘于图 4中.其中, 2002年10月4日地基观测数据来源于MillstoneHill非相干散射雷达(IncoherentScatterRadar, ISR), Athens数字测高仪台站只提供2004年7月2日的峰值电子密度和峰值高度, 其地基观测结果是由Chapman函数拟合得到的.
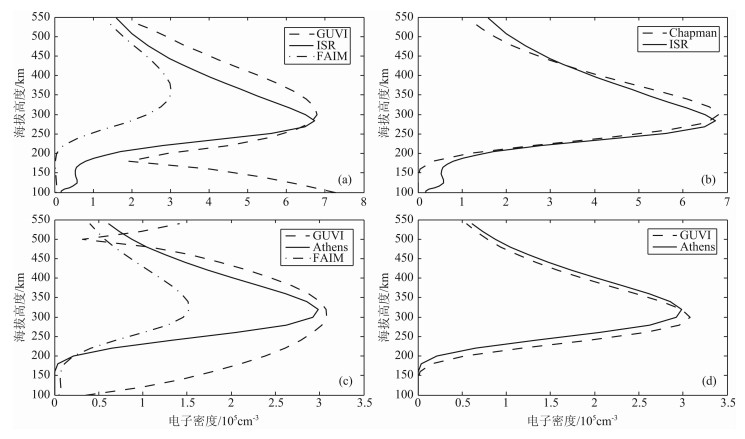
|
图 4 反演结果 (a)2002年10月4日反演结果;(b)2002年10月4日Chapman拟合结果;(c)2004年7月2日反演结果;(d)2004年7月2日Chapman拟合结果. Fig. 4 Retrieved results for selected locations (a) There trieved EDP for Oct 4, 2002; (b) The Chapman function fitted EDP for Oct 4, 2002; (c) There trieved EDP for Jul 2, 2004;(d) The Chapman function fitted EDP for Jul 2, 2004. |
|
|
表 1 位置参数列表 Table 1 Parameters of selected locations |
如图 4a和4c所示, 与全解析性电离层模型FAIM相比, 本研究得到的结果在海拔200km以上与地基方式探测结果更为接近, 然而, 在海拔高度200km以下, 却与其结果相差甚远.造成此现象的原因可能有两个:一是海拔高度200km以下, 未考虑中和作用在氧原子135.6nm夜气辉辐射中的影响; 二是GUVI观测资料和地基探测结果在空间(经度上相差7°左右)和时间上并非完全一致.尽管海拔200km以下本研究反演得到的电子密度偏差很大, 但是其峰值电子密度和峰值高度吻合得很好.
一般情况下, 可用Chapman函数来描述电离层中的电子密度[17]
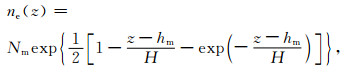
|
(13) |
其中, z为海拔高度, Nm和hm分别为峰值电子密度和峰值高度, 标高H取值为54km.将本研究计算得到的峰值电子密度和峰值高度代入式(13)中, 得到Chapman型电子密度剖面, 如图 4b所示.由图 4b和4d可见, 利用本研究提出的正则化解法得到峰值电子密度和峰值高度, 结合Chapman型表达式得到的电子密度剖面与地基方式探测结果符合得很好.
综上所述, 利用正则化与牛顿迭代相结合的方法由远紫外夜气辉OI135.6nm光谱数据反演得到的自由形式EDP, 与全解析性电离层模型FAIM结果相比, 具有明显的优越性, 但是其与地基观测结果, 尤其是在海拔200km以下仍存在一定差异.尽管如此, 本研究得到的峰值电子密度和峰值高度与地基观测结果吻合得很好.因此, 利用本研究方法得到的电子密度剖面代替传统电离层探测方法, 弥补了非相干散射雷达和数字测高仪台站稀少, 难以实时获得高空间分辨力全球电离层电子密度结构和特性的不足.
4.2 NmF2随磁暴变化分析利用本研究提出的算法反演了2002年9月29日到10月3日GUVI探测得到的5°N处的夜气辉数据, 初步分析电离层电子密度随磁暴的变化情况.国际上, 一般采用Dst指数来描述磁暴:-50 < Dst≤-30为小磁暴, -100 < Dst≤-50为中等磁暴, -200 < Dst≤-100为大磁暴, Dst≤-200为特大磁暴.图 5中绘出了2002年9月29日到10月3日的Dst (来源于美国国家海洋大气局NOAA)变化曲线.从图 5可以看出, 9月29日处于磁宁静期, 9月30日发生了小磁暴, 10月1日发生了大磁暴, 10月2日到10月3日为磁暴的恢复相, Dst指数开始回升.
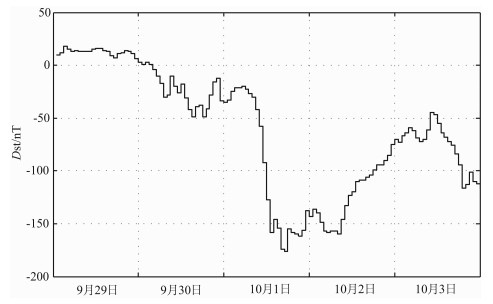
|
图 5 2002年9月29日-10月3日Dst指数变化 Fig. 5 Dst index for Sep 29-Oct 3, 2002 |
如图 6所示为反演得到的2002年9月29日到10月3日EDPs, 在图像横轴下方标注数据的确切经度和获取时间, 当存在轨道缺失时采用邻近插值得到所需数据且不标记其经度和获取时间.在此, 以磁宁静期9月29日(图 6a)为参考, 初步分析磁暴对电离层电子密度的影响情况.
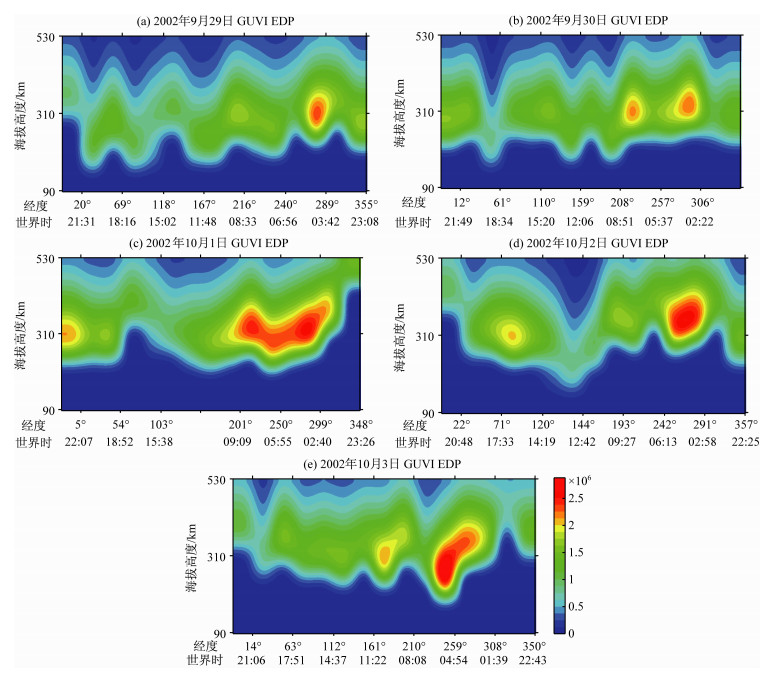
|
图 6 2002年9月29日-10月3日反演结果 Fig. 6 Retrieved EDPs for Sep 29-Oct 3, 2002 |
9月30日凌晨4时起Dst指数显著下降, 持续到10时在-20nT附近上下波动.如图 6b所示, 经度208°~257°附近出现电离层赤道异常(Equatorial Anomaly)峰值高度处的电子密度明显大于9月29日相应位置值; 13:00到20:00发生了小磁暴, 相应位置处的电子密度较9月29日也有所提升.
10月1日3时至10时Dst指数在-20~-40nT范围内波动, 西半球经度201°~299°附近电离层赤道异常区范围显著变大(图 6c); 之后Dst指数迅速下降, 并在17时左右达到最小值, Dst指数在-160nT上下起伏并一直持续到午夜, 电离层F层的电子密度普遍变大, 且向上抬升.
凌晨到下午16时10月2日的Dst指数比10月1日的更小, 因此在2002年10月2日(图 6d)西半球经度242°~291°内的电离层赤道异常范围较10月1日进一步扩大, 然而在193°~242°内的电子密度却有所下降.16时以后Dst指数开始回升, 峰值高度或峰值电子密度出现大范围下降.2002年10月3日Dst指数继续回升, 如图 6e所示赤道异常普遍减弱.
经分析2002年9月29日到10月3日5°N处的EDPs随磁暴的变化情况发现, 随着磁暴的发生及其强弱变化, 在峰值高度附近会出现电离层赤道异常, 其变化程度和影响范围在各经度处不尽相同.
5 结论本研究利用全球远紫外成像光谱仪GUVI获得的氧原子135.6nm夜气辉光谱辐射数据, 建立了临边观测模型, 采用正则化与牛顿迭代法相结合的方法, 计算得到了自由形式电离层电子密度; 将自由形式电离层电子密度的峰值高度和峰值电子密度与Chapman型表达式相结合, 得到了Chapman拟合电子密度, 并将其与地基观测数据及全解析性电离层模型FAIM进行了比较.结果表明, 在海拔高度200km以上本研究得到的电子密度与地基观测数据符合得很好, 但在200km以下偏差较大, 产生这一现象的原因有待进一步研究.
利用本研究提出的算法反演得到了2002年9月29日到10月3日5°N处的EDPs, 初步分析电离层电子密度随磁暴的变化情况发现, 随着磁暴的发生及其强弱变化, 在峰值高度附近会出现电离层赤道异常, 其变化程度和影响范围在各经度处不尽相同.
致谢感谢美国霍普金斯大学和美国TIMED/GUVI卫星的数据支持.
| [1] | 吴健, 郭兼善. 空间天气对通信和导航定位等无线电系统有什么影响?. 全球定位系统 , 1999, 24(3-4): 1–4. Wu J, Guo J S. What effects does space weather have on radio systems?. GNSS World of China (in Chinese) , 1999, 24(3-4): 1-4. |
| [2] | Dymond K F, Thonnard S E, McCoy R P, et al. An optical remote sensing technique for determining nighttime F region electron density. Radio Sci. , 1997, 32(5): 1985-1996. DOI:10.1029/97RS01887 |
| [3] | Rajesh P K, Liu J Y, Hsu M L, et al. Ionospheric electron content and NmF2 from nighttime OI 135.6nm intensity. J. Geophys. Res. , 2011, 116(A02313): 1-16. |
| [4] | Paxton L J, Morrison D, Strickland D J, et al. The use of far ultraviolet remote sensing to monitor space weather. Adv. Space Res. , 2003, 31(4): 813-818. DOI:10.1016/S0273-1177(02)00886-4 |
| [5] | Wang J, Tang Y, Tang L J, et al. Retrieval of ionospheric O/N2 based on FUV imaging data. SPIE , 2009, 7498: 74982N-1-74982N-9. |
| [6] | 彭圣锋, 唐义, 王静, 等. 远紫外光谱遥感反演热层O/N2技术研究. 光谱学与光谱分析 , 2012, 32(5): 1296–1300. Peng S F, Tang Y, Wang J, et al. Research on retrieving thermospheric O/N2 from FUV remote sensing. Spectroscopy and Spectral Analysis (in Chinese) , 2012, 32(5): 1296-1300. |
| [7] | 王咏梅, 付利平, 王英鉴. 星载远紫外极光/气辉探测发展综述. 地球物理学进展 , 2008, 23(5): 1474–1479. Wang Y M, Fu L P, Wang Y J. Review of space-based FUV aurora/airglow observations. Progress in Geophysics (in Chinese) , 2008, 23(5): 1474-1479. |
| [8] | Paxton L J, Christensen A B, Morrison D, et al. GUVI: a hyperspectral imager for geospace. SPIE , 2004, 5660: 228-240. |
| [9] | Jeffrey S D. Inversion of nighttime electron densities using satellite observations. New Mexico: New Mexico Institute of Mining and Technology, 2001. |
| [10] | Hanson W B. Radiative recombination of atomic oxygen ions in the nighttime F region. J. Geophys. Res. , 1969, 74(14): 3720-3722. DOI:10.1029/JA074i014p03720 |
| [11] | McDonald S E. Day to day and longitudinal variability of the nighttime low latitude terrestrial ionosphere. Fairfax: George Mason University, 2007. |
| [12] | DeMajistre R, Paxton L J, Morrison D, et al. Retrievals of nighttime electron density from Thermosphere Ionosphere Mesosphere Energetics and Dynamics (TIMED) mission Global Ultraviolet Imager (GUVI) measurements. J. Geophys. Res. , 2004, 109(A5): 1-14. |
| [13] | 吴杰, 李明峰, 余腾. 测量数据处理中病态矩阵和正则化方法. 大地测量与地球动力学 , 2010, 30(4): 102–105. Wu J, Li M F, Yu T. Ill matrix and regularization method in surveying data processing. Journal of Geodesy and Geodynamics (in Chinese) , 2010, 30(4): 102-105. |
| [14] | 王振杰, 欧吉坤. 用L-曲线法确定岭估计中的岭参数. 武汉大学学报(信息科学版) , 2004, 29(3): 235–238. Wang Z J, Ou J K. Determining the ridge parameter in a ridge estimation using L-curve method. Geomatics and Information Science of Wuhan University (in Chinese) , 2004, 29(3): 235-238. |
| [15] | 蒋德明, 董超华. 大气廓线物理反演的最优化方法进展. 地球科学进展 , 2010, 25(2): 133–139. Jiang D M, Dong C H. A review of optimal algorithm for physical retrieval of atmospheric profiles. Advances in Earth Science (in Chinese) , 2010, 25(2): 133-139. |
| [16] | Solomon S C. Modeling of the thermosphere-ionosphere system. Phys. Chem. Earth , 2000, 25(5-6): 499-503. |
| [17] | 梅冰, 万卫星. 基于Millstone Hill非相干散射雷达观测的电离层电子浓度剖面的经验正交函数分析. 地球物理学报 , 2008, 51(1): 10–16. Mei B, Wan W X. An empirical orthogonal function (EOF) analysis of ionospheric electron density profiles based on the observation of incoherent scatter radar at Millstone Hill. Chinese J. Geophys. (in Chinese) , 2008, 51(1): 10-16. |
 2013, Vol. 56
2013, Vol. 56