2. 长安大学地质工程与测绘学院, 西安 710054
2. College of Geology Engineering and Geomatics, Chang ′an University, Xi′an 710054, China
中心回线装置和大定源装置是应用最广泛的瞬变电磁探测方法之一, 近年来在煤田采空区探测、金属矿勘察等领域发挥了重要作用.其探测方法是在地面敷设一正方形或矩形不接地回线作为发射线圈, 线圈内供矩形脉冲电流, 电流关断后, 在线圈内和线圈外测量由地下低阻地质体引起的感应二次场, 通过分析二次场得到低阻地质体的位置和深度.
瞬变电磁正演是研究瞬变电磁响应规律的有效途径.随着计算机技术的应用, 瞬变电磁正演方面有了很快的发展.目前常采用的正演算法主要有一维线性数字滤波法, 二维、2.5维有限差分法和有限元法、三维积分方程法、时域有限差分法等[1].一维层状模型的正演技术经过多年的发展已经相当成熟[2-4].在积分方程正演方面, 殷长春等[5]、唐新功等[6]基于张量格林函数的体积分方程对三维异常体的瞬变电磁响应进行了正演模拟, 并对瞬变电磁的探测能力进行了分析, 前者的研究还考虑了瞬变电磁的激电效应.Zhdanov等[7-8]、SanFilipo等[9]对复杂模型进行了三维积分方程正演, 前者考虑了非均匀背景电阻率并对复杂模型的偶极瞬变电磁响应特征进行了分析, 后者则重点分析了三维异常体的瞬变电磁响应特征.Cox等[10]也采用体积分方程法对航空电磁数据进行三维正演计算.在有限差分、时域有限差分正演方面, 宋维琪等[11]采用有限差分法对电偶源瞬变电磁进行了三维正演计算.Commer和Newman[12-13]采用并行有限差分法建立了电偶源瞬变电磁三维正演算法.Oristaglio等[14], 闫述等[15]采用duFort-Frankel有限差分方法研究了二维地电断面下线源产生的瞬变电磁场, 并分析了均匀半空间中包含二维异常体时的瞬变电磁场分布特征.闫述等[15]、石显新等[16]还研究了低阻覆盖层对瞬变电磁场分布的影响.Wang等[17-18]、肖怀宇[19]、陈丹丹[20]采用改进的DuFort-Frankel有限差分形式建立了三维时间域正演算法, 其算法采用地面均匀半空间瞬变电磁场的解析解作为初始条件加入到迭代方程中, 并对多种三维模型进行了分析.岳建华等[21]、杨海燕等[22]采用电偶源激发进行了矿井瞬变电磁探测三维时域有限差分正演.Haber等(2007)[23], Oldenburg等(2008)[24], Yang等(2012)[25]则采用有限体积法进行了时间域航空瞬变电磁的三维正演工作.此外, 也有许多学者采用有限单元法或者其他方法进行瞬变电磁场的三维正演模拟[26-29].综合不同方法的优势与缺点, 并考虑到任意三维复杂模型的正演问题, 时域有限差分法被认为是一种有潜力的三维正演方法.前人采用时域有限差分的研究过程中均基于二次场的计算, 没有考虑一次场部分, 以初始条件的方式加入负阶跃脉冲的解析解作为激励源.这种使用初始条件作为激励源的方式不能适用于两种情况:第一, 表层电阻率不均匀的模型不能采用均匀半空间的解析解来近似; 第二, 进行隧道超前探测时, 发射线圈位于隧道掌子面上, 该情况不存在解析解也无法进行简化得到解析解.采用初始条件的方式施加激励源的另一个局限是地面向下一定范围内只能按照均匀半空间的模型进行设计, 无法正确地反应浅层的地质信息.
由于观测设备的限制, 不能做到数学上以delta函数表示的阶跃关断, 由于关断时间的存在使实际勘探中瞬变电磁响应与阶跃脉冲模拟的响应存在差别.在瞬变电磁的关断时间方面, 国内外许多学者也进行较多的研究.早在1972年, Verma[30]就研究了6种不同输入波形对导体球的瞬变电磁响应, 同期, Pathor[31]对极化半空间在锯齿函数和斜阶跃函数下的瞬变电磁响应进行了研究.Raiche[32]专门针对关断时间中的斜阶跃函数进行了讨论, 给出了层状模型瞬变电磁响应的影响规律.Fitterman和Anderson[33]也研究了发射机关断时间对瞬变电磁测深的影响.Qian[34]将下降沿宽度和发射机测量时间之间构成时窗并分析了单极性脉冲和双极性脉冲两种不同时窗的瞬变电磁响应.Poddar与Anderson[35]研究了发射机的关断效应以及接收机的频带宽度对视电阻率的影响.于生宝和林君[36]针对瞬变电磁发射机的关断时间进行了研究并通过硬件改进实现了较小的关断时间.嵇艳鞠等[37-38]针对ATTEM系统求解了关断电流期间的瞬变电磁场, 并提出了校正方法, 形成了软件系统.白登海和Meju[39]研究了线性关断电流和指数关断电流对瞬变电磁响应的影响并给出了相应的校正方法.杨海燕和岳建华[40]针对多匝线圈的关断效应与校正问题进行了专门的研究, 并对线性和半正弦关断函数的响应特征进行了分析.杨云见等[41-42]采用将斜阶跃响应分割为多个小电流元的方法进行考虑关断时间的瞬变电磁一维正演, 并进行了马奎特反演.前人针对关断时间影响的研究主要集中在关断时间的校正, 均采用一维模型.但实际的地质模型应当是复杂的三维模型, 三维复杂模型中关断时间对瞬变电磁衰减曲线的影响尚未见报道.
另外, 随着仪器技术、航空电磁以及M-TEM的发展, 对不同发射波形的瞬变电磁响应也提出了新的要求, 部分航空电磁勘探以及新兴的M-TEM方法要求进行on-time的测量.为了弥补原有方法的不足和适应新型探测方法的正演要求, 本文以文献[17]的方法为基础, 直接采用时域有限差分方程进行推导, 并进行了两点改进:第一, 通过将矩形回线源电流密度加入麦克斯韦方程组的安培环路定理方程, 实现回线源瞬变电磁激发源加入; 第二, 在激发电流源的计算中考虑关断时间.文献[17]的激发源是以均匀半空间模型在关断后非常短的某一时刻, 地面及地下一定范围内的电场作为初始条件加入的, 这就要求地面在一定深度范围内是均匀的, 本文的第一点改进使时域有限差分方程考虑了一次场的计算, 并且源的计算不再依赖均匀半空间模型响应作为初始条件, 而是首先在计算区域内通过电流源的激发和电磁场在有耗媒质中的传播特性形成一次场, 这样就可以考虑地表电阻率的不均匀性和模型的任意复杂性.另外, 由于实际观测中不可能出现阶跃电流的关断形式, 第二点改进可以设置激发电流波形和下降沿, 通过设置不同的关断时间, 可以研究关断效应对三维复杂模型瞬变电磁响应的影响规律.为了验证论文算法的可行性和程序的可靠性, 采用建立的方法进行回线源瞬变电磁三维正演, 均匀半空间模型计算结果与解析解对比、四种典型三层模型计算结果与线性数字滤波解对比、均匀半空间包含三维低阻块体模型计算结果与积分方程解[43]对比, 并且与Wang[17]的计算结果进行了对比, 证明论文改进的时域有限差分方法可行并且精度可靠.考虑关断时间对瞬变电磁响应存在较大影响, 以H模型为例计算了不同关断时间中心点的感应电动势衰减曲线, 与负阶跃脉冲的线性数字滤波解进行对比, 发现关断时间的存在对晚期瞬变电磁衰减曲线影响较小, 对早期衰减曲线影响较大, 关断时间越小, 早期的计算结果越接近负阶跃脉冲的线性数字滤波解, 关断时间越大, 早期的计算结果与线性数字滤波解偏差较大, 就丧失了对浅层地质体的分辨能力, 因而缩短关断时间对于提高瞬变电磁勘探早期结果的可用性具有重要意义, 这一结论与前人采用一维方法研究[32, 39]的结论是相同的, 说明本文建立的三维方法对关断时间的考虑是合理的.以实际地质资料为基础, 构建包含两层采空区的三维复杂模型, 以1μs的极短关断时间进行了复杂模型定回线源瞬变电磁响应计算.
2 控制方程 2.1 无源区域的电磁场方程准静态条件下, 均匀、有耗、非磁性、无源媒质中的麦克斯韦方程组为

|
(1a) |
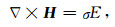
|
(1b) |
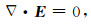
|
(1c) |
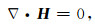
|
(1d) |
其中E为电场强度, H为磁场强度, B为磁通量密度, σ为电导率, t为时间.
对方程(1a)取旋度, 并考虑(1c)可以得到电场的扩散方程, 类似的也可以得到磁场的扩散方程, 分别为
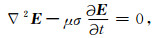
|
(2) |
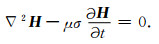
|
(3) |
前人的研究已经表明, 阻尼波动方程和扩散方程是可以通过准静态条件相互转化.在一定的边界条件下, 可以使用阻尼波动方程的解来代替扩散方程的解[14].
瞬变电磁勘探中一般忽略位移电流[44], 因而其电磁场问题符合准静态条件下的麦克斯韦方程组[3].
由于忽略了位移电流, 方程(1b)缺少电场对时间的导数, 无法构成FDTD计算所需要的显式的时间步进格式.由于FDTD数值计算的需要, 并根据阻尼波动方程与扩散方程的相互转化关系, 人为地加入一项虚拟位移电流, 将方程(1b)变为
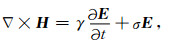
|
(4) |
其中, γ具有介电常数的量纲, 本文称其为虚拟介电常数, γ的取值需要满足一定的稳定性条件.部分学者的研究发现引入该虚拟位移电流项并给定合适的取值能够放松FDTD迭代过程中对时间网格的划分要求, 并且不影响计算结果[17].事实上, 如果不进行准静态近似而直接采用麦克斯韦方程组进行求解并取大地的实际介电常数, 同样能够得到合理的结果, 这是因为在有耗的大地中电磁场的波动特性会很快消失而只剩下电磁场的扩散特性, 但是由于迭代稳定性的要求, 时间步要求非常短, 总的计算时间将会达到难以忍受的程度.例如, 取灰岩的相对介电常数为7, 按照10 m的立方体网格计算, 为了满足Courant稳定性条件要求, 最大的时间网格必须小于8.8232×10-9s.如果计算1ms的纯二次场响应至少需要进行113338步迭代, 这将导致程序占用大量的计算资源.
引入虚拟位移电流后, 麦克斯韦方程组的时域有限差分离散与未进行准静态近似的Maxwell方程组的离散方式类似.在直角坐标系中对Maxwell方程组中(1a)和方程(4)写成分量的形式为[45]
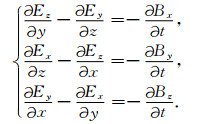
|
(5) |
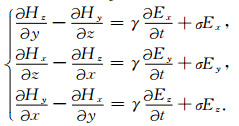
|
(6) |
Chew和Wang[17]的研究发现, 在进行电磁场数值计算的过程中, Maxwell方程组中的第四方程(1b)必须显式包含在迭代过程中, 否则对低频电磁场的计算结果是不可靠的.因而, 对于磁场的计算, 可以通过电场先求解磁场的x和y两个分量, 然后通过这两个分量以及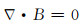
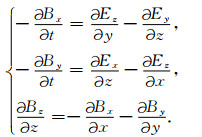
|
(7) |
方程(6)和(7)即为无源区域电磁场计算的基本方程.
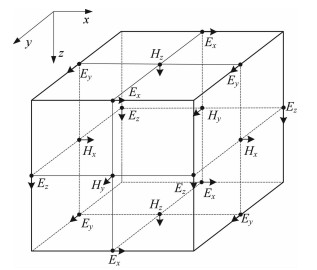
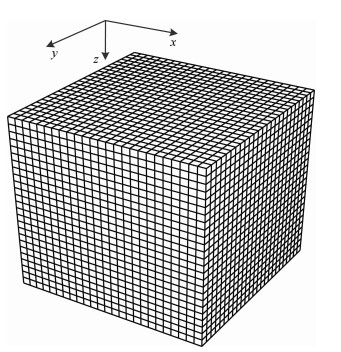
如图 1所示, Yee元胞格式中电场和磁场分布在不同的位置, 每个电场周围都有4个磁场分量, 同样每一个磁场周围都有4个电场分量包围, 形成电磁场的交替迭代模式.采用图 1的Yee元胞格式和坐标系进行均匀网格划分(图 2), 每个立方体网格表面的中心设置为磁场分量, 这样地面上可以恰好设置每个网格的中心点作为垂直磁场分量的接收点.
|
图 1 FDTD计算采用的Yee晶胞格式 Fig. 1 A typical Yee Grid in FDTD |
|
图 2 均匀网格剖分示意图 Fig. 2 Schematic diagram of uniform subdivision using Yee grid |
将电场和磁场对时间和空间的一阶偏导数采用中心差分近似可以得到离散的电场、磁场迭代格式, 详细的差分格式表达式请参见文献[45]第12-16页.磁场的z分量由于采用了不同的离散方程其形式与文献[45]中不同, 根据Oristaglio的方法将其离散得
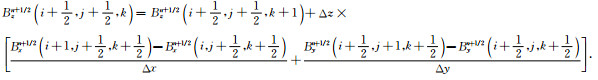
|
(8) |
式中的磁场分量节点位置与文献[45]相同.
2.2 激励源的施加与文献[17, 19-20]中采用初始条件的方法加入激励源不同, 本文采用回线中加入阶跃电流的方式进行加载, 考虑激发电流的上升沿、持续时间和下降沿.由于FDTD计算需要一个平滑的开始来保证稳定性, 为了方便与负阶跃脉冲激励下的瞬变电磁响应进行对比, 采用梯形波的发射电流波形.在有源区域, Maxwell方程组中的(1b)修改为
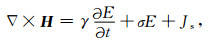
|
(9) |
其中, Js为源电流密度.
采用如图 3所示的网格分布施加回线源, 回线源采用电流密度施加在网格线上, 与电场分量的空间位置重合.根据图 1中的坐标系及网格划分形式, 有源区域方程(9)的直角坐标分量形式为
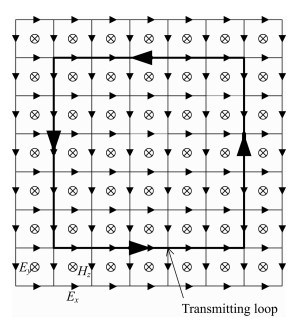
|
图 3 回线源与网格位置示意图 Fig. 3 Relative position of the loop source and the grids on the ground |
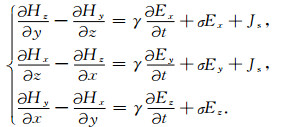
|
(10) |
以中心差分格式离散方程(10)并整理, 考虑软源的加入方式将发射回线所在网格仍然按照差分格式进行正常迭代[46], 可得到电场迭代的FDTD形式:
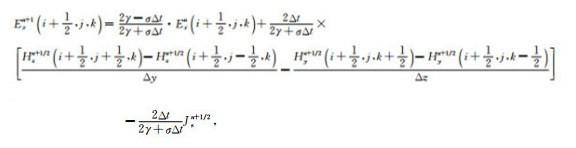
|
(11a) |
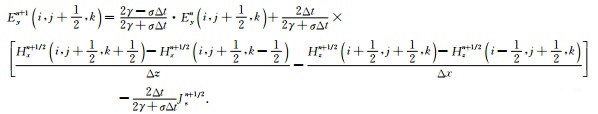
|
(11b) |
激发源加载方式仅与电场的x和y分量有关, 因而Ez的迭代公式与无源区域的相同.实际进行数值计算的过程中, 将梯形波施加到回线源中, 上升沿和下降沿采用线性变化, 由于上升沿和下降沿导致电磁场剧烈变化, 因而需要足够短的迭代时间步来保持稳定, 根据笔者的计算, 采用1μs的上升沿和下降沿时, 采用1ns的时间步可以满足稳定.当只关心下降沿的作用时, 为了得到一个平滑的上升过程, 可以采用正弦波形或者指数波形作为上升沿函数.图 4给出了一种典型的梯形波发射电流波形示意图, 发射电流上升沿、电流持续时间以及下降沿按照图中的时间段给出.
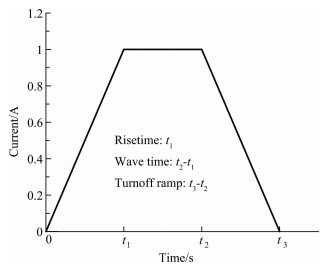
|
图 4 梯形发射电流示意图 Fig. 4 Schematic diagram of trapezoidal transmitter current |
对于无源区域和有源区域可以分别采用上述的方程进行迭代计算, 但回线源瞬变电磁的激发源是细导线, 在实际建模中细导线的尺寸远小于晶胞尺寸, 因而不能通过晶胞来模拟细导线, 由于回线的存在, 源所在的单元网格需要进行特殊的处理.基于有源区域的Maxwell方程, 实际建模时将发送线圈与电场分量的空间位置重合(如图 5所示), 因而临近单元仅需要处理网格中心的磁场分量[45].
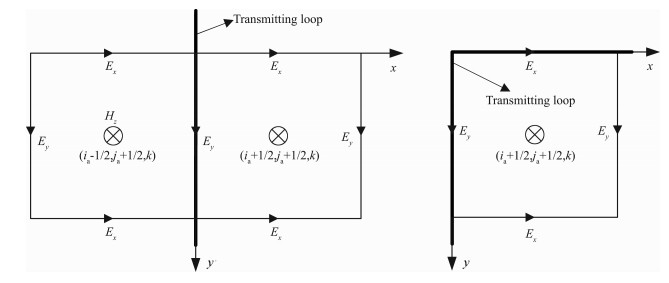
|
图 5 细导线与相邻单元的位置示意图 (a)发射回线与网格位置示意; (b)发射回线角点与网格位置示意. Fig. 5 Schematic diagram of transmitter loop and the grid (a)Relative positionbetweenthe transmitter loop and the grid; (b)Relative positionbetweenthe transmitter loop and the grid at the bending part |
根据法拉第电磁感应定律和安培环路定理, 有对于某一时刻, 发送回线附近的环向磁场和径向电场按照1/r的规律变化, 其中r为距导线中心的距离.如图 5所示, 使用方程(12)和(13)可以求得源所在网格环路的场值.由于导线临近单元的磁场仅与该元胞表面的电场分量和上一时刻的磁场分量有关, 本例中仅需要求解Hz分量, 而前面为了保证FDTD对低频电磁场求解的正确性, 没有采用电场分量求解Hz而是采用磁场的x和y分量来求解z分量, 论文中的处理方法恰好回避了源所在网格的特殊处理要求.
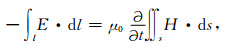
|
(12) |

|
(13) |
进行FDTD计算时必须满足Courant稳定性条件, 针对三维FDTD问题, 均匀网格剖分下的Courant稳定性条件为
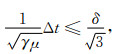
|
(14) |
其中, δ表示均匀网格剖分时的网格尺寸.
整理上式可以得到时间网格划分的条件
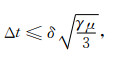
|
(15) |
从方程(15)可以看出, 通过适当放大虚拟介电常数γ的值可以使时间间隔Δt的取值适当增大, 减少迭代次数.当γ取值为真实介电常数时, 上式即为电磁场波动方程的稳定性条件.事实上, γ的取值又取决于时间网格Δt的取值.方程(15)的另一个形式是

|
(16) |
γ与Δt的相互依赖关系使问题更加复杂.虚拟位移电流是为了方便构建显式的FDTD差分格式而引入的, 必须对虚拟位移电流项进行适当的限制以保证其不致于太大而淹没了扩散场的特性.Oristaglio和Hohmann在分析二维du Fort-Frankel差分格式时给出了对虚拟位移电流的限制条件[14].结合三维问题可以得到

|
(17) |
根据Wang和Hohmann[17]的经验, 时间网格按照下式进行划分:
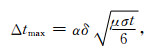
|
(18) |
控制系数α的取值为0.1到0.2.t取值自关断电流后开始取值.实际实现过程中, 先按照方程(18)得到满足要求的时间网格, 然后通过方程(16)求解合适的虚拟介电常数, 以此来满足Courant稳定性要求.为了保证激发源能够产生合适的一次场, 在开始至电流关断的时间范围内采用真实介电常数代替γ并采用等间距时间网格剖分.
在外边界条件以及地空边界条件的施加上, 本文采用与文献[17]相同的方法.地空边界条件中, 将地面的磁场向空中延拓半个网格的高度, 根据电磁波在空气中满足的拉普拉斯方程进行求解, 在进行地面电场迭代时, 使用得到的空中半个网格处的磁场进行计算.模型的另外5个外边界上, 分别设置电场的切向分量和磁场的垂向分量为0.
采用上述的稳定性条件和外边界, 笔者对301× 301×100个网格的模型进行FDTD计算时发现可以迭代十几万步而不发散.
3 模型验证为了验证本文建立的回线源瞬变电磁三维FDTD正演算法及程序的可靠性, 分别对均匀半空间模型、四类典型三层模型、均匀半空间包含三维低阻块体模型进行了计算与对比.
3.1 均匀半空间解析解与三维FDTD解的对比以100Ωm的均匀半空间为对比模型, 发射线圈采用70m×70m的方形回线, 激发电流1A, 上升沿、下降沿均为1μs, 脉冲持续时间为5ms.如果采用占空比为1:1的双极性矩形脉冲时, 相当于50 Hz的发送频率.计算模型采用10m的均匀网格剖分, 模型x、y、z方向的网格数为301×301×100.在解析解的求解过程中, 将方形回线按照等效磁矩折算成圆形回线计算.图 6分别给出了均匀半空间解析解与三维时域有限差分解的感应电动势衰减曲线对比和视电阻率曲线对比图以及各自的相对误差.从图中可以看出, 在早期时间得到的感应电动势衰减曲线与解析解差别较大, 计算相对误差时发现早期最大相对误差达到45%, 这主要是由于解析解场源采用负阶跃脉冲函数, 而FDTD解考虑了关断时间的影响.随着时间推移, 10μs之后的时间, 感应电动势衰减曲线吻合较好, 相对误差在5%以下.采用晚期视电阻率公式计算得到的视电阻率曲线在较早的时间范围内差异较大, 晚期吻合较好, 晚期视电阻率曲线的相对误差均在3.5%以下.
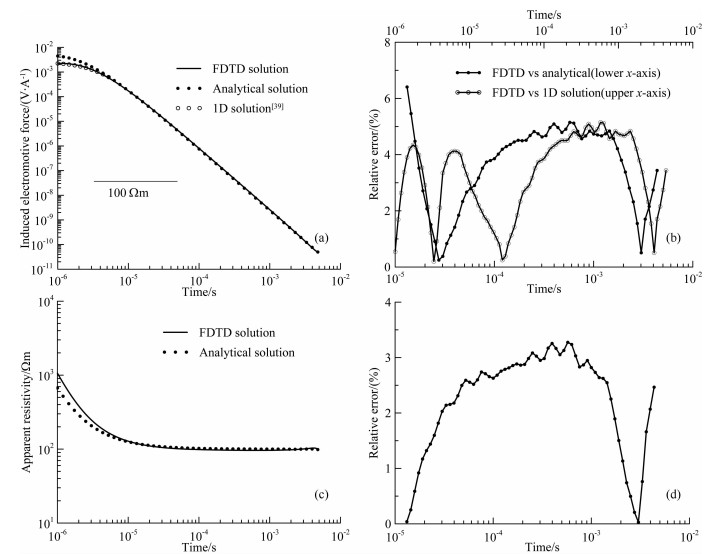
|
图 6 均匀半空间模型FDTD解与解析解计算结果对比曲线 (a)感应电动势衰减曲线; (b)感应电动势相对误差; (c)视电阻率曲线; (d)视电阻率相对误差. Fig. 6 Comparisonbetween the FDTD solution and the analytical solution of a homogeneous half-space model (a)Decay curves of the EMF; (b)Relative error of the EMF decay curves; (c)The apparent resistivity curves; (d)Relative error of the apparent resistivity |
为了进一步对比说明本文给出的考虑关断时间的三维计算方法的可靠性, 作者采用文献[39]中给出的方法进行了均匀半空间条件下考虑关断时间的瞬变电磁正演, 在图 6a中给出了采用该方法计算得到的衰减曲线, 并给出了早期阶段的相对误差(见图 6b), 由于FDTD解与解析解在早期存在较大的误差, 为了更好地体现晚期的相对误差, 在图 6b中采用底部的横坐标轴, 时间范围为10μs~5ms; 文献[39]中提供的方法考虑了关断时间的影响, 因而其早期响应与本文考虑关断时间的三维FDTD解差别较小, 为了体现出全部计算时间内的相对误差, 该误差曲线采用顶部的坐标轴作为横坐标, 时间范围为1μs~5ms.
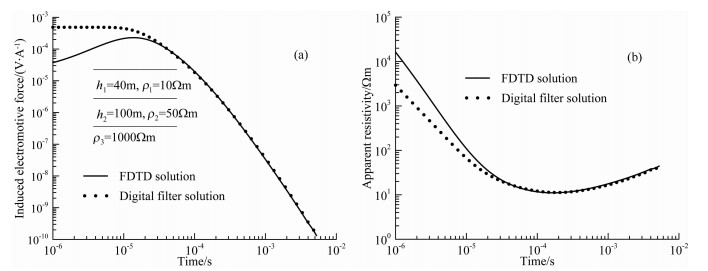
3.2 三层模型计算结果对比选取A、H、K、Q四种典型三层模型, 将三维FDTD解与负阶跃脉冲的线性数字滤波解进行对比.除地电参数外, 其余计算参数与均匀半空间模型计算时采用的参数相同.四种模型的每层厚度和电阻率参数分别绘制在相应的衰减曲线对比图中.图 7-10分别给出了这四种三层模型的感应电动势衰减曲线和视电阻率曲线对比结果.
|
图 7 A型模型的FDTD解与线性数字滤波解对比曲线 (a)感应电动势衰减曲线; (b)视电阻率曲线. Fig. 7 Comparison between the FDTD solution and the digital filter solution for A type model (a)Decay curves of the EMF; (b)The apparent resistivity curves |

|
图 8 H型模型的FDTD解与线性数字滤波解对比曲线 (a)感应电动势衰减曲线; (b)视电阻率曲线. Fig. 8 Comparison between the FDTD solution and the digital filter solution for H type model (a)DecaycurvesoftheEMF; (b)Theapparentresistivitycurves. |
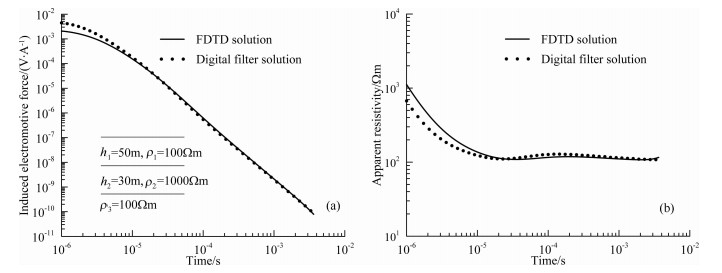
|
图 9 K型模型的FDTD解与线性数字滤波解对比曲线 (a)感应电动势衰减曲线; (b)视电阻率曲线. Fig. 9 Comparison between the FDTD solution and the digital filter solution for K type model (a)Decay curves of the EMF; (b)The apparent resistivity curves |
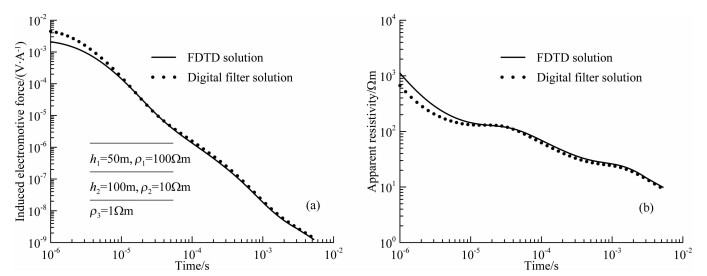
|
图 10 Q型模型的FDTD解与线性数字滤波解对比曲线 (a)感应电动势衰减曲线; (b)视电阻率曲线. Fig. 10 Comparison between the FDTD solution and the digital filter solution for Q type model (a)Decay curves of the EMF; (b)The apparent resistivity curves |
通过图 7-10中四种模型的感应电动势衰减曲线与视电阻率曲线对比可以看到, 三维FDTD计算模型得到的感应电动势衰减曲线与负阶跃脉冲的线性数字滤波解仅在早期存在较大的差异, 晚期两条曲线吻合较好, 在双对数坐标系中几乎重合.层状模型的线性数字滤波解并不是真正的解析解, 从四种模型的视电阻率曲线对比图中可以看出, 三维FDTD计算结果得到的视电阻率曲线明显地反应了该类型地层模型的视电阻率特征, 并且与成熟的一维层状模型正演结果吻合较好, 论文建立的改进的三维FDTD正演方法是有效的.
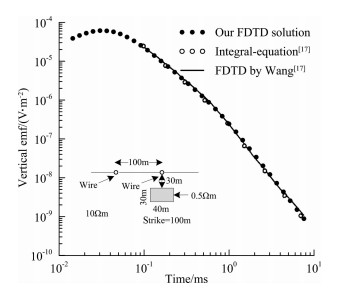
3.3 均匀半空间中存在低阻三维块体模型结果对比为了验证改进的FDTD算法与原算法的一致性, 选取文献[17]中包含三维低阻块体的均匀半空间模型进行计算对比.Wang在文献[17]中采用该模型将三维FDTD解与Newman的积分方程解进行了对比.本文亦采用该模型进行计算并且与Wang的三维FDTD解以及Newman的积分方程解进行对比验证.
将Wang在文献[17]中的计算结果截图并将本文三维FDTD解采用相同的坐标系进行绘制得到如图 11所示的对比结果图.Wang与Newman给出的计算结果是从0.1ms开始的, 本文除给出Wang计算结果的全部时刻曲线外还给出了该模型早期(0.01~0.1ms)的计算结果.从图中可以看出本文的FDTD计算结果与Wang的计算结果吻合非常好, 并且与积分方程计算结果也吻合较好, 晚期的响应本文的计算结果更接近积分方程解.
|
图 11 包含三维低阻块体的均匀半空间模型对比 Fig. 11 Comparison of 3D low resistivity body in a homogeneous half-space model |
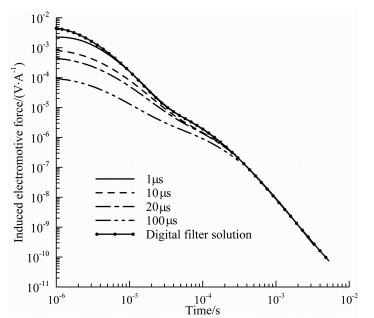
瞬变电磁勘探中, 关断时间是考察采集设备的一项重要指标, 越短的关断时间就越接近基本理论的负阶跃脉冲假设.通过对前述计算模型的对比发现, 关断时间对采集的信号存在较大的影响.由于多数情况下的勘探更关心地下低阻体的响应特征, 选取具有代表意义的H模型进行不同关断时间的三维数值模拟, 并将计算结果与一维层状模型线性数字滤波解进行对比.采用与图 8相同的模型与观测参数, 设置关断时间分别为1μs、10μs、20μs和100μs. 图 12给出了不同关断时间影响下线圈中心点的感应电动势衰减曲线.
|
图 12 采用三维FDTD计算的H模型中心点不同关断时间的感应电动势衰减曲线 Fig. 12 Central vertical decay curves with different ramp times for a H model by 3D FDTD solution |
从图中可以看到, 关断时间越小, 计算结果越接近负阶跃脉冲的线性数字滤波解, 关断时间越大, 早期的响应曲线与滤波解差异越大, 并且感应电动势数值越小.关断时间越大, “早期影响”持续时间越长, 即“关断效应”越明显, 这一点与前人采用一维方法研究[32, 39]的结论是相同的, 说明本文建立的三维方法对关断时间的考虑是合理的.图中关断时间为100μs时, 0.3ms以前的信号均不能正常反应实际地电模型的感应电动势衰减规律.而关断时间为1μs时, 可以认为自4μs之后的信号能够反应实际的地电模型.所以, 如果在实际的工作中想使用采集的早期信号就必须进行适当的校正, 文献[32-33, 39-40, 42]针对一维问题提出了多种校正方法, 但是对于三维复杂模型情况下关断时间的影响规律以及现有校正方法的适用性仍有待于进一步的研究.
5 三维复杂模型回线源瞬变电磁响应三维时域有限差分正演的真正意义在于其对任意复杂介质瞬变电磁响应的正演模拟能力.前面的分析与对比已经验证了论文建立的考虑关断时间的瞬变电磁三维时域有限差分正演方法的可靠性, 能够适应三维复杂模型的正演计算.以某煤矿真实地层为基础进行简化, 设计了如图 13所示的含有两层煤、两层采空区的三维复杂模型, 两煤层间存在砂页岩, 详细的地电参数以及地质体尺寸列于表 1.

|
图 13 两层采空区复杂模型示意图 Fig. 13 Diagram of a complexmodel with two mined out water bodies |
|
|
表 1 两层采空区复杂模型参数 Table 1 Parameters of a complex model with two mined out water bodies |
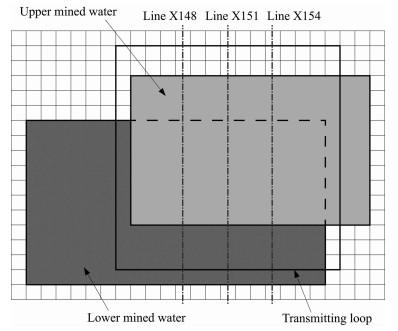
图 14给出了该复杂模型的俯视图, 结合三维示意图 13可以明确定位煤层与采空区的位置.模型设计仍然采用301×301×100的10m立方体均匀网格, 设计采用150m的发射线框.进行数值计算时可以方便设置多点阵列式接收, 针对本模型定回线源的方式提取了图 14中所示的Line X148、Line X151、Line X154共3条测线的结果进行分析, 每条测线的测点按照网格在Y方向的编号进行设置, 这样设计测线和测点的编号恰好与网格的x坐标和y坐标重合, 发射回线恰好在模型正中间, 过回线中心点的测线为Line X151线.
|
图 14 两层采空区复杂模型俯视图与发射回线位置和测线布置 Fig. 14 Top view of the complex model with two mined out water bodies and the position of the transmitting loop and the survey line arrangement |
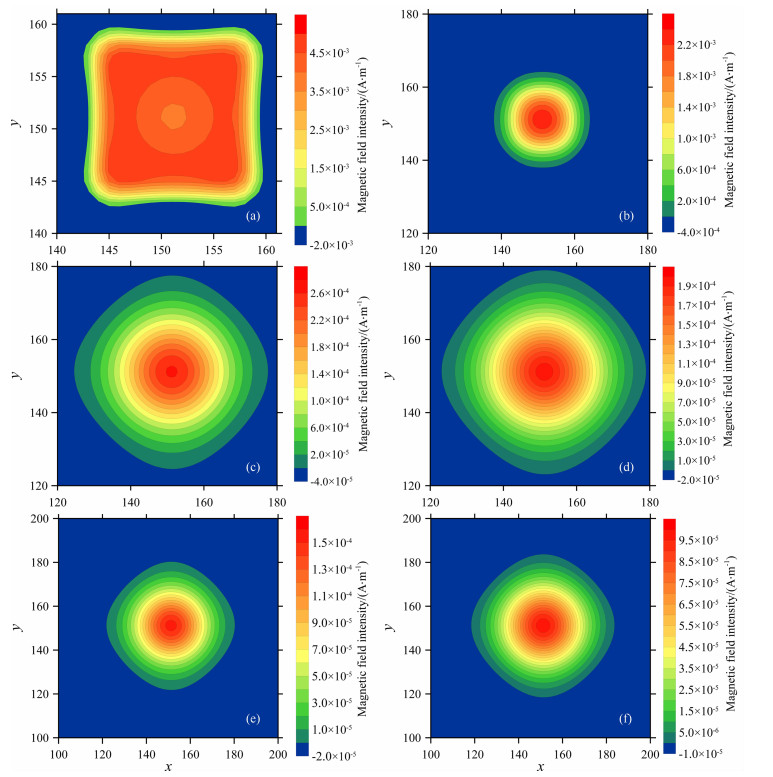
为了更好地表现电流关断后不同时刻地面的磁场分布以及磁场的向外扩散过程.选定关断后1、10、100、200、400、1000μs共6个时刻绘制了地面垂直磁场强度分布等值线图(图 15).由于采用均匀网格的划分方式, 图中给出的等值线图是没有经过插值的各点实际计算值.可以看出, 在电流关断前以及刚刚关断很短的时间内, 地面磁场分布围绕回线中心呈矩形, 与发射回线的形状相同, 随着时间的推移, 逐渐退化为圆形, 磁场强度的数值也由发射回线处最大逐渐变化为中心点最大, 并且随着时间的推移, 地面不同位置的磁场强度差异越来越小, 这显示了磁场的扩散消退过程.
|
图 15 不同时刻地面垂直磁场分布 (a)关断后1μs; (b)关断后10μs; (c)关断后100μs; (d)关断后200μs; (e)关断后400μs; (f)关断后1000μs. Fig. 15 Distribution of vertical magnetic on the earth surface at different times (a)1μs after turn off; (b)10μs after turn off; (c)100μs after turn off; (d)200μs after turn off; (e)400μs after turn off; (e)1000μs after turn off |
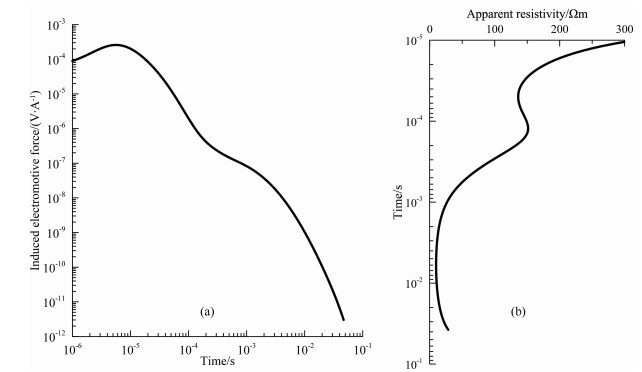
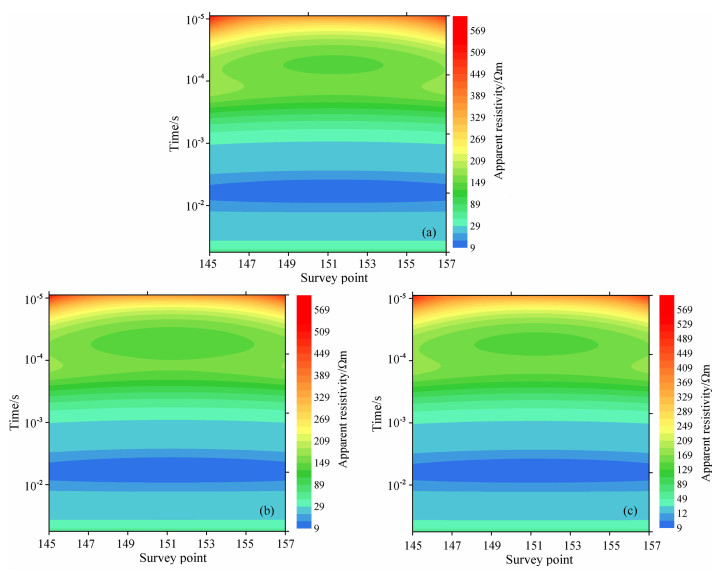
将回线中心点的衰减曲线在双对数坐标下成图(图 16a), 从衰减曲线可以看出明显的异常, 由于存在关断时间, 早期的衰减曲线存在一段抬升之后迅速衰减.从关断后10μs开始采用晚期视电阻率公式计算了中心点的视电阻率曲线(图 16b), 从视电阻率曲线中可以明显地看到两层低阻体的存在, 第一层低阻体位于40μs左右, 第二层低阻体位于1~7ms左右, 在7ms以后视电阻率逐渐变大, 说明探测深度已经达到了模型的石英砂岩层(高阻层).对选定的3条测线分别进行数据处理并绘制视电阻率等值线图(图 17).由于采用的测点超出了回线边长1/3的范围, 视电阻率等值线断面图中两侧的测点存在一定的边框效应, 但这并不影响本例中对模拟结果的分析.三条视电阻率等值线图显示在40μs左右存在一层低阻异常, 在7ms左右存在另一层低阻异常体.针对Line X148测线和Line X154测线, 以测点151为中心, 这两条测线的视电阻率断面中第一层低阻体并不完全对称, 右侧的低阻体明显大于左侧, 且第一层低阻体的规模明显小于Line X151测线中的第一层低阻体规模.这与模型设计是相符合的.
|
图 16 中心点感应电动势与视电阻率曲线 (a)中心点感应电动势; (b)中心点视电阻率. Fig. 16 Induced electromotive force and apparent resistivity curve of the central point (a)The EMF at the loop center and(b)the corresponding apparent resistivity |
|
图 17 选定测线的视电阻率等值线断面 (a)Line X148测线视电阻率等值线图; (b)Line X151测线视电阻率等值线图; (c)Line X154测线视电阻率等值线图. Fig. 17 Apparent resistivity time contours of the selected lines (a)Apparent resistivity contours of line X148; (b)Apparent resistivity contours of line X151; (c)Apparent resistivity contours of line X154. |
采用三维时域有限差分法对回线源瞬变电磁正演进行了求解, 引入虚拟位移电流项以构建显式时域有限差分格式, 以矩形回线的方式改进了激发源, 并考虑一次场计算和关断下降沿的影响.对三类模型进行了计算与结果对比.以H模型为例采用三维算法计算了不同关断时间的衰减曲线形态.设计了一个包含两层采空区的三维复杂模型并进行正演计算.得到以下结论:
(1)将回线源电流密度加入迭代方程代替初始条件激发源, 模型不再依赖表层电阻率均匀的假设, 因而算法具有更广泛的适用性.论文建立的正演方法能够进行任意复杂模型的三维瞬变电磁正演.在改进地空边界条件后有望实现起伏地形的三维正演.
(2)论文建立的方法能够合理进行关断效应的三维模拟.由于关断时间的影响, 三维时域有限差分结果与均匀半空间解析解早期存在较大差别, 晚期信号一致, 说明关断时间仅对早期的瞬变电磁响应信号存在较大影响, 而对晚期的瞬变电磁响应信号影响不大.对于同一模型, 关断时间的长短与早期的感应电动势幅值存在明显的关系.关断时间越短, 早期的感应电动势信号越接近负阶跃脉冲的计算结果.考虑关断时间的衰减曲线更接近实际仪器采集的衰减曲线.关断效应对于三维复杂模型的影响规律还有待进一步研究.
致谢作者在瞬变电磁三维时域有限差分正演研究过程中与TsiliWang进行了许多有益的讨论, 并得到了许多好的建议, 在此表示衷心的感谢.作者还要感谢两位匿名审稿专家的专业评述和修改建议.
| [1] | 薛国强, 李貅, 底青云. 瞬变电磁法正反演问题研究进展. 地球物理学进展 , 2008, 23(4): 1165–1172. Xue G Q, Li X, Di Q Y. Research progress in TEM forward modeling and inversion calculation. Progress in Geophysics (in Chinese) , 2008, 23(4): 1165-1172. |
| [2] | Anderson W L. Numerical integration of related Hankel transforms of orders 0 and 1 by adaptive digital filtering. Geophysics , 1979, 44(7): 1287-1305. DOI:10.1190/1.1441007 |
| [3] | 李貅. 瞬变电磁测深的理论与应用. 西安: 陕西科学技术出版社, 2002 . Li X. Theory and Application of Transient Electromagnetic Sounding (in Chinese). Xi′an: Shaanxi Science & Technology Press, 2002 . |
| [4] | 朴化荣. 电磁测深法原理. 北京: 地质出版社, 1990 . Piao H R. Theory of Electromagnetic Sounding (in Chinese). Beijing: Geological Publishing House, 1990 . |
| [5] | 殷长春, 刘斌. 瞬变电磁法三维问题正演及激电效应特征研究. 地球物理学报 , 1994, 37(S1): 486–492. Yin C C, Liu B. The research on the 3D TDEM modeling and IP effect. Chinese J. Geophys (in Chinese) , 1994, 37(S1): 486-492. |
| [6] | 唐新功, 胡文宝, 严良俊. 层状地层中三维薄板的瞬变电磁响应. 石油地球物理勘探 , 2000, 35(5): 628–633. Tang X G, Hu W B, Yan L J. Transient electromagnetic response to a 3-D thin plate in a layered earth. Oil Geophysical Prospecting (in Chinese) , 2000, 35(5): 628-633. |
| [7] | Zhdanov M S, Lee S K, Yoshioka K. Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity. Geophysics , 2006, 71(6): G333-G345. DOI:10.1190/1.2358403 |
| [8] | Hursán G, Zhdanov M S. Contraction integral equation method in three-dimensional electromagnetic modeling. Radio Sci , 2002, 37(6): 1089. |
| [9] | SanFilipo W A, Hohmann G W. Integral equation solution for the transient electromagnetic response of a three-dimensional body in a conductive half-space. Geophysics , 1985, 50(5): 798-809. DOI:10.1190/1.1441954 |
| [10] | Cox L H, Wilson G A, Zhdanov M S. 3D inversion of airborne electromagnetic data using a moving footprint. Exploration Geophysics , 2010, 41(4): 250-259. DOI:10.1071/EG10003 |
| [11] | 宋维琪, 仝兆歧. 3D瞬变电磁场的有限差分正演计算. 石油地球物理勘探 , 2000, 35(6): 751–756. Song W Q, Tong Z Q. Forward finite differential calculation for 3-D transient electromagnetic field. OilGeophysical Prospecting (in Chinese) , 2000, 35(6): 751-756. |
| [12] | Newman G A, Commer M. New advances in three dimensional transient electromagnetic inversion. Geophysical Journal International , 2005, 160(1): 5-32. |
| [13] | Commer M, Newman G. A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources. Geophysics , 2004, 69(5): 1192-1202. DOI:10.1190/1.1801936 |
| [14] | Oristaglio M L, Hohmann G W. Diffusion of electromagnetic fields into a two-dimensional earth: A finite-difference approach. Geophysics , 1984, 49(7): 870-894. DOI:10.1190/1.1441733 |
| [15] | 闫述, 陈明生, 傅君眉. 瞬变电磁场的直接时域数值分析. 地球物理学报 , 2002, 45(2): 275–284. Yan S, Chen M S, Fu J M. Direct time-domain numerical analysis of transient electromagnetic fields. Chinese J. Geophys (in Chinese) , 2002, 45(2): 275-284. |
| [16] | 石显新, 闫述, 陈明生. 瞬变电磁勘探中的低阻层屏蔽问题. 煤炭学报 , 2005, 30(2): 160–163. Shi X X, Yan S, Chen M S. Study on screening of conductive bed in transient electromagnetic prospecting. Journal of China Coal Society (in Chinese) , 2005, 30(2): 160-163. |
| [17] | Wang T, Hohmann W G. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling. Geophysics , 1993, 58(6): 797-809. DOI:10.1190/1.1443465 |
| [18] | Wang T, Tripp A C, Hohmann G W. Studying the TEM response of a 3-D conductor at a geological contact using the FDTD method. Geophysics , 1995, 60(4): 1265-1269. DOI:10.1190/1.1443859 |
| [19] | 肖怀宇.带地形的瞬变电磁法三维数值模拟[硕士论文].北京:中国地质大学, 2006. Xiao H Y. Three Dimensional Numerical Modeling Considering the Topography of TEM(in Chinese). Beijing: China University of Geoscience, 2006. http://cdmd.cnki.com.cn/Article/CDMD-11415-2006060022.htm |
| [20] | 陈丹丹.瞬变电磁法三维正演研究[硕士论文].北京:中国地质大学, 2008. Chen Dandan. Study of Three-Dimensional Forward of TEM(in Chinese). Beijing: China University of Geosciences, 2008. http://cdmd.cnki.com.cn/Article/CDMD-11415-2008068733.htm |
| [21] | 岳建华, 杨海燕, 胡搏. 矿井瞬变电磁法三维时域有限差分数值模拟. 地球物理学进展 , 2007, 22(6): 1904–1909. Yue J H, Yang H Y, Hu B. 3D finite difference time domain numerical simulation for TEM in mine. Progress in Geophysics (in Chinese) , 2007, 22(6): 1904-1909. |
| [22] | 杨海燕, 岳建华. 巷道影响下三维全空间瞬变电磁法响应特征. 吉林大学学报(地球科学版) , 2008, 38(1): 129–134. Yang H Y, Yue J H. Response characteristics of the 3D Whole2Space TEM disturbed by roadway. Journal of Jilin University(Earth Science Edition) (in Chinese) , 2008, 38(1): 129-134. |
| [23] | Haber E, Oldenburg D W, Shekhtman R. Inversion of time domain three-dimensional electromagnetic data. Geophysical Journal International , 2007, 171(2): 550-564. DOI:10.1111/gji.2007.171.issue-2 |
| [24] | Oldenburg D W, Haber E, Shekhtman R. Forward modelling and inversion of multi-source TEM data. SEGTechnical Program Expanded Abstracts , 2008, 27(1): 559-563. |
| [25] | Yang D K, Oldenburg D W. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit. Geophysics , 2012, 77(2): B23-B34. DOI:10.1190/geo2011-0194.1 |
| [26] | Um Evan S, Harris J M, Alumbaugh D L. 3D time-domain simulation of electromagnetic diffusion phenomena: A finite-element electric-field approach. Geophysics , 2010, 75(4): F115-F126. DOI:10.1190/1.3473694 |
| [27] | Best M E, Duncan P, Jacobs F J, et al. Numerical modeling of the electromagnetic response of three-dimensional conductors in a layered earth. Geophysics , 1985, 50(4): 665-676. DOI:10.1190/1.1441941 |
| [28] | Zaslavsky M, Druskin V, Knizhnerman L. Solution of 3D time-domain electromagnetic problems using optimal subspace projection. Geophysics , 2011, 76(6): F339-F351. |
| [29] | Brner R U, Ernst O G, Spitzer K. Fast 3-D simulation of transient electromagnetic fields by model reduction in the frequency domian using Krylov subspace projection. Geophys. J. Int , 2008, 173(3): 766-780. DOI:10.1111/gji.2008.173.issue-3 |
| [30] | Verma S K. Transient electromagnetic response of a conducting sphere excited by different types of input pulses. Geophysical Prospecting , 1972, 20(4): 752-770. DOI:10.1111/gpr.1972.20.issue-4 |
| [31] | Rathor B S. Transient electromagnetic field of a polarizable half-space due to various current pulses. Geophysical Prospecting , 1978, 26(2): 337-351. DOI:10.1111/gpr.1978.26.issue-2 |
| [32] | Raiche A P. The effect of ramp function turn-off on the TEM response of layered earth. Exploration Geophysics , 1984, 15(1): 37-41. DOI:10.1071/EG984037 |
| [33] | Fitterman D V, Anderson W L. Effect of transmitter turn-off time on transient soundings. Geoexploration , 1987, 24(2): 131-146. DOI:10.1016/0016-7142(87)90087-1 |
| [34] | Qian B. Analysis and improvement of the primary field waveform of the ground TEM method. Geophysical Prospecting , 1987, 35(2): 197-204. DOI:10.1111/gpr.1987.35.issue-2 |
| [35] | Poddar M, Anderson Walter L. Transient electromagnetic modeling of shallow A-type sections with 3-D inhomogeneities. Geophysics , 1992, 57(6): 774-780. DOI:10.1190/1.1443291 |
| [36] | 于生宝, 林君. 瞬变电磁法中发射机关断时间的影响研究. 石油仪器 , 1999, 13(6): 15–17. Yu S B, Lin J. Study of the effect of transmitter turn-off time on transient electromagnetic method. Petroleum Instruments (in Chinese) , 1999, 13(6): 15-17. |
| [37] | 嵇艳鞠, 林君, 于生宝, 等. ATTEM系统中电流关断期间瞬变电磁场响应求解的研究. 地球物理学报 , 2006, 49(6): 1884–1890. Ji Y J, Lin J, Yu S B, et al. A study on solution of transient electromagnetic response during transmitting current turn-off in the ATTEM system. Chinese Journal of Geophysics (in Chinese) , 2006, 49(6): 1884-1890. |
| [38] | 嵇艳鞠, 林君, 程德福, 等. ATEM-Ⅱ瞬变电磁仪数据处理软件的研制与应用. 吉林大学学报(地球科学版) , 2003, 33(2): 242–245. Ji Y J, Lin J, Cheng D F, et al. Development and application of data processing software of ATEM-Ⅱ transient electromagnetic instrument. Journal of Jilin University(Earth Science Edition) (in Chinese) , 2003, 33(2): 242-245. |
| [39] | 白登海, MejuMaxwell. 瞬变电磁法中两种关断电流对响应函数的影响及其应对策略. 地震地质 , 2001, 23(2): 245–251. Bai D H, Meju Maxwell. The effect of two types of turn-off current on tem responses and the correction techniques. Seismology and Geology (in Chinese) , 2001, 23(2): 245-251. |
| [40] | 杨海燕, 岳建华. 瞬变电磁法中关断电流的响应计算与校正方法研究. 地球物理学进展 , 2008, 23(6): 1947–1952. Yang H Y, Yue J H. Research on response calculation and correction technique of turn-off current in the transient electromagnetic method. Progress in Geophysics (in Chinese) , 2008, 23(6): 1947-1952. |
| [41] | 杨云见, 王绪本, 何展翔. 考虑关断时间效应的瞬变电磁一维反演. 物探与化探 , 2005, 29(3): 234–236. Yang Y J, Wang X B, He Z X. 1D inversion of transient electromagnetic data in consideration of ramp time effect. Geophysical and Geochemical Exploration (in Chinese) , 2005, 29(3): 234-236. |
| [42] | 杨云见, 王绪本, 何展翔. 瞬变电磁法中的斜阶跃波效应及常规的几种校正方法分析. 物探化探计算技术 , 2006, 28(2): 129–132. Yang Y J, Wang X B, He Z X. The effect discussion of ramp time and some general corrective methods of transient electromagnetic method. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2006, 28(2): 129-132. |
| [43] | Newman G A, Hohmann G W, Anderson W L. Transient electromagnetic response of a three-dimensional body ina layered earth. Geophysics , 1986, 51(8): 1608-1627. DOI:10.1190/1.1442212 |
| [44] |
牛之琏.
时间域电磁法原理. 长沙: 中南大学出版社, 2007 .
Niu Z L.
Theory of Time Domian Electromagnetic (in Chinese). ( |
| [45] | 葛德彪, 闫玉波. 电磁波时域有限差分方法. (第二版). 西安: 西安电子科技大学出版社, 2005 . Ge D B, Yan Y B. Finite Difference Time Domain Method of Electromagnetic Wave (in Chinese). Xi′an: Xidian University Press, 2005 . |
| [46] | 余文华, 苏涛, RajM, 等. 并行时域有限差分. 北京: 中国传媒大学出版社, 2005 . Yu W H, Su T, Raj M, et al. Parallel Finite Difference Time Domain Method (in Chinese). Beijing: Communication University of China Press, 2005 . |
 2013, Vol. 56
2013, Vol. 56



