2. 陕西延长石油集团有限责任公司研究院, 西安 710075
2. Research Institute, Shaanxi Yanchang Petroleum(Group) Co., LTD, Xi'an 710075, China
目前, 地震数据的全体积拉平分析技术已经成为刻画地质沉积特征、分析岩性地层圈闭油气藏的有效工具[1-3].传统的以时间(或者深度)切片的方式来解释三维地震数据, 尤其在检测和分析地质沉积特征时, 存在明显的缺陷.由于受到地质构造起伏变形的影响, 许多地质沉积结构的埋藏深度随着空间展布会发生很大的变化, 反应在地震数据上单个时间切片很难贯穿一个完整的反射层.因此在研究某个特定的反射层时, 需要同时观察一组时间切片, 并且需要解释人员通过记忆联络沉积结构在每个时间切片上的局部特征, 这就为三维地震资料的解释带来很多不便.如果能够逆转地质构造过程的作用, 使地震反射同相轴按年代地层顺序呈水平展布, 就可以使得河道砂体等沉积结构得到更加直观的显示.地震数据的全体积拉平技术正是解决这一问题的有效途径[2].在拉平后的数据体中, 输入数据转化为按地质年代先后顺序排列的地层结构, 所有的沉积结构呈现为水平展布, 通过单一的时间切片就可以显示同一反射层内的完整信息, 极大地方便了河道砂体等沉积结构的解释.为了便于叙述, 我们在文中将输入数据的水平切片称为“时间切片”, 将拉平数据的水平切片称为“地质时间切片”.
地震数据的拉平处理是通过消除同相轴的局部倾角来实现的, 通常按逐地震道调整输入数据中的采样点, 使得同一同相轴中的对应采样点沿水平面对齐.这种采样点的调整方式包括平移和内插操作, 因而输入数据中的每一道在拉平数据中会表现出局部区域的拉伸或者压缩现象.各种地震数据的拉平方法均可看作从不同的角度解决原始数据与拉平数据的采样点之间映射关系的问题.常规基于层位解释的拉平方法是根据解释人员对感兴趣的地质沉积目标所属的地震反射层的预判, 在地震数据体中追踪出一条或者多条同相轴[4-6].这种方法不仅要求解释人员熟悉相关区块的地质沉积环境, 且非常耗时耗力; 此外, 拉平过程由于仅有采样点的时间平移操作, 只能拉平预先追踪的同相轴, 无法控制其他同相轴的空间展布情况.
近年来地震数据的全体积自动拉平技术取得了较大的进展, 基于对地震同相轴不同的自动追踪途径, 发展出多种全体积拉平方法.Stark[7-8]通过瞬时相位解缠绕的方法实现三维地震数据的全体积拉平, 将解缠绕后的瞬时相位的等相面与地震层位相对应, 并在此基础上引入了“相对地质时间”的概念. Pauget等[9]构造相关矩阵建立相邻地震道中同相轴之间的连接关系, 进而通过一种代价函数优化地震同相轴的全局连接关系.在这类全体积拉平方法中, 基于局部地层倾角的地震同相轴自动追踪方法得到许多研究者的关注.在de Groot等[10-11]与de Bruin等[12]建立的层序地层解释体系中, 以两个已知层位作为顶底界面所限定的范围内, 基于地层倾角信息将参考地震道所有采样点对应的层位进行外推, 最后按Wheeler图形[13]的存储方式得到年代地层数据体. Lomask等[14-15]建立一种关于地层倾角的非线性偏微分方程, 应用Gauss-Newton法计算输入数据的采样点相比参考地震道的相对时间偏移量.Fomel[16]将地震数据体的预测着色理论用于地震同相轴的自动拾取和拉平, 基于地层倾角数据将选定的参考地震道的信息向三维空间进行扩展.前述几种方法均需要一个参考地震道进行全体积拉平, 为了得到较为准确的拉平映射, 必须要求该参考地震道贯穿所有沉积体, 这在实际操作中往往不可行.Parks等[17]在前人工作的基础上建立起一种基于局部地层倾角的线性反演机制, 避免了拉平对参考地震道的依赖, 实现了更准确快捷的地震数据全体积拉平.
Parks等提出的基于局部地层倾角的地震全体积拉平技术, 其前提假设即能够获得具有较高精确度的地层倾角数据, 而在遇到含有复杂地质构造的地震数据时, 该假设往往不能成立.多数倾角估计方法在断层等构造引起的地层倾角突变的区域会给出偏差较大的估计结果, 从而造成拉平数据在这些区域出现较大的畸变, 进而影响到全数据域的同相轴拉平效果.本文基于Parks等提出的地震数据拉平的线性反演机制, 通过采用一种高精度的地层倾角估算方法获得观测数据, 并在最小二乘模型中引入误差模板控制迭代反演过程中产生残差的数据区域, 从而实现更为有效的地震数据的全体积拉平.这种拉平方法可较好地兼顾有效同相轴的拉平效果和拉平数据整体的相对保真性, 在处理复杂构造的地震数据时避免产生较大的畸变(如信号结构的过拉伸或过压缩等), 得到具有良好可解释性的拉平数据.
2 方法原理 2.1 全体积拉平的数学模型对三维地震数据作拉平处理时, 要求拉平数据中的采样点数与原始数据中的采样点数据完全相同, 因而拉平后的地震数据可看作对原始数据采样点的某种重新排布(平移或者插值).设初始的三维输入数据为f(t, x, y), 拉平处理后的数据为g(τ, x, y), 则它们之间存在一一映射关系:
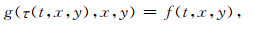
|
(1) |
其中, t表示输入数据的垂直坐标, 即时间或深度; τ表示输出数据的垂直坐标, 即相对地质时间, 其数值大小代表了地震层位按地质年代沉积的先后顺序.这一关系的成立需满足两条前提假设[17] :(1)对地震数据作拉平时只需将输入数据的采样点沿垂直方向重新排布; (2)输入数据中的地震层位可以在拉平数据中用某个常τ水平切面近似表示.根据这两条前提假设可见, 地震数据拉平的主要过程即沿垂直方向移动调整采样点(t, x, y), 使输入数据中的垂直坐标t转换为输出数据中的相对地质时间坐标τ, 两种坐标尺度之间满足:

|
(2) |
其中, σ(t, x, y)表示采样点(t, x, y)在拉平前后的位置偏移量, 它和相对地质时间τ均是输入数据垂向坐标t的函数.
通过式(2)将地震数据的拉平处理转化对各个采样点对应的偏移量σ的求解问题.因此, 如何利用地震数据中包含的信息, 求解参数σ成为地震拉平的关键.本文采用Parks等[17]建立的局部地层倾角与偏移量之间的关系, 即当给定输入数据中沿主测线和联络测线的局部地层倾角p(t, x, y)和q(t, x, y)时, 它们与偏移量σ(t, x, y)之间满足偏微分方程组
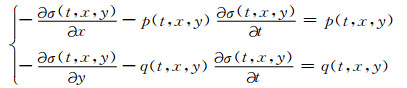
|
(3) |
偏微分方程组(3)根据地震层位在三维空间的地层倾角分布情况, 将各个采样点沿垂直方向进行平移调整来消除该空间位置的地层倾角, 从而实现对地震层位的拉平处理.然而, 求解偏微分方程组(3)将面临两方面的问题:首先, 如何获得较为精确的输入数据, 即局部地层倾角p(t, x, y)和q(t, x, y); 其次, 方程组(3)的输入变量多于输出变量, 如何建立合适的反演模型求解该超定问题.本文就这两个问题进行了分析讨论, 给出相应的解决方案.
2.2 加权向量滤波法估算地层倾角基于局部地层倾角的地震数据拉平方法, 认为倾角数据包含了原始地震数据中地层结构的全部信息, 将地层倾角作为拉平处理的唯一输入数据, 因此需要要求对局部地层倾角的估算具有较高的精确度.目前有多种可用于局部地层倾角估计的方法, 如局部倾斜叠加方法[18], 平面波分解滤波器法[19-20], 基于相干度量的扫描搜索法[21-22], 以及梯度结构张量法[23-24]等.这些方法大多没有将断层、不整合等地层边缘区域与地震同相轴延展良好的区域区别对待, 将断层区域的倾角估计为断层两侧同相轴的平均倾向.这种断层区域的倾角估计误差, 会通过拉平过程扩散开来, 造成断层两侧较大范围内的拉平误差.本文采用Wang等[25]提出的加权向量方向滤波法(Weighted Vector Directional Filter, WVDF)估计局部地层倾角, 该方法不仅保持了同相轴延展良好区域倾角估计的一致性, 而且可有效提高断层等地层边缘区域以及地层倾角突变区域的倾角估计精确度.
WVDF方法首先通过数值方法计算各个采样点处的梯度向量, 并按照事先选定的某个参考方向对梯度向量进行旋转, 然后以目标点为中心划定一个局部分析窗, 通过对窗内所有旋转调整后的梯度向量进行加权平均来估计目标点处的局部地层倾角向量,
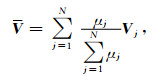
|
(4) |
其中, v表示目标点所属同相轴的法向向量, N为目标窗内采样点的总数, Vj为分析窗内依照参考方向旋转后的梯度向量, μ j为梯度向量Vj的自适应加权系数, 它的大小取决于向量Vj在分析窗内的全局角度距离,
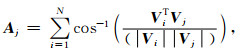
|
(5) |
通过这种自适应加权策略, WVDF方法在断层、不整合等地层边缘区域以及地层倾角突变区域表现出相比几种常规方法更为优异的地层倾角估算性能[25], 可以为后续拉平偏移量的反演计算提供更准确的观测数据, 得到更好的地层拉平效果.
2.3 优化全体积拉平反演模型在建立方程组(3)的反演求解模型前, 为了后续分析推导的方便, 将该方程组采用矩阵形式表示.记三维地震数据体沿时间、主测线和联络测线方向的采样点数分别为Nt、Nx和Ny, 那么数据体总的采样点数即为N=Nt×Nx ×Ny.首先, 将待求取的N个模型参数σ(t, x, y)按一定顺序排列成模型向量M,

|
(6) |
其中,

|
(7) |
即将按照常规三维地震数据排列形式表示的模型参数σ(t, x, y)重新按照逐道逐测线顺序排列的方式表示为模型列向量M.
同样地, 方程组(3)的右端项可写成由局部地层倾角p和q组成的数据向量D,
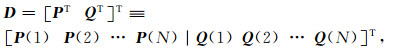
|
(8) |
其中,
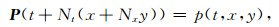
|
(9) |
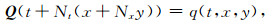
|
(10) |
类似地, 即将按照常规三维地震数据排列形式表示的地层倾角数据p(t, x, y)和q(t, x, y)重新按照逐道逐测线顺序排列的方式表示为数据列向量P和Q.
另外, 将方程组(3)左端的偏微分算子采用数值算子代替, 可写成矩阵形式为
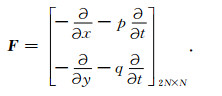
|
(11) |
最后, 结合式(6)-(11)的定义即可以将偏微分方程组(3)写成矩阵形式:
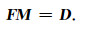
|
(12) |
方程组(12)以拉平位置偏移量σ为待求模型向量M, 沿主测线和联络测线的地层倾角p、q为观测向量D, 方程组(3)左端的偏微分算子为前向算子F, 构成一个典型线性系统的矩阵表达形式.容易看出方程组(12)包含N个未知数, 2N个方程, 是一个超定方程组, 若求解其最小二乘解, 那么对应的目标函数可写成:
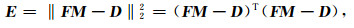
|
(13) |
其中, T表示矩阵的转置.
2.3.1 目标区域优化在对实际地震数据作拉平处理时, 由于噪声或断层等复杂地质构造的影响, 由式(13)给出的目标函数很难获得理想的拉平效果.通过对二次误差函数进行加权优化可以较好地解决这一问题[26], 针对观测数据不同的数据品质, 分配不同的加权值, 以提高反演结果的质量.这里主要考虑断层对拉平处理的影响, 一方面断层两侧同相轴的不连续性会给误差函数引入较大的整体误差, 另外, 断层结构自身的复杂性会导致拉平模型的第一条假设条件不成立.因此, 需要构造一个能够反映断层位置和同相轴性态的误差模板, 使其在断层区域取值较小, 而在连续的同相轴区域取值较大, 从而降低断层对拉平效果的影响.本文采用Bakker[27]提出的基于梯度结构张量的面型结构置信度量c(t, x, y)作为误差函数的加权系数.面型结构置信度量值c(t, x, y)在闭区间[0, 1]内取值, 在地震同相轴局部呈平面结构的区域接近于1, 而在断层等地层边缘和混沌结构区域接近于0.通过面型结构置信度量的取值大小, 就可以反映同相轴的可拉平性态, 近似判断出断层的位置.结合目标函数(13)式, 由c(t, x, y)构造误差函数的加权矩阵模板为
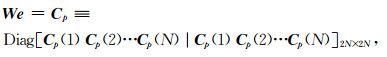
|
(14) |
其中,
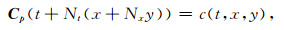
|
(15) |
即将按照常规三维地震数据排列形式表示的面型结构置信度量c(t, x, y)重新按照逐道逐测线顺序排列的方式表示为参数列向量Cp.
此时, 目标函数(13)转变为
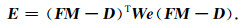
|
(16) |
理想的拉平处理效果要求拉平后的地震同相轴尽可能保持原有的波形形态, 即需要要求位置偏移量σ为关于原始数据垂直坐标的光滑函数.因此, 在目标函数(16)中需要进一步增加关于偏移量σ的光滑性约束项, 避免拉平过程出现严重的波形发散或者覆盖现象.其中, “波形发散”是指在原始数据的地震道中相距较近的采样点在拉平后映射到相距较远的位置, 使得拉平数据在这些位置之间有信息空缺, 即波形的过度放大; “波形覆盖”是指原始数据的地震道中多个不同的采样点经过拉平后映射到相近的位置上, 采样点的信息由于互相覆盖而损失, 即波形的过度压缩.本文采用偏移量σ关于垂直坐标t的一阶偏导数来度量其光滑性[26], 从而更新目标函数(16)为
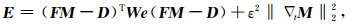
|
(17) |
其中, 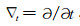
式(17)中的目标函数为关于模型向量M的严格凸函数, 其对应的极小值求解问题可经过简单的数学推导转化为如下线性方程组的求解问题:
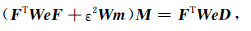
|
(18) |
其中, 
为了减少计算共轭梯度法计算过程中的迭代次数, 加快收敛速度, 本文采用模型参数重新参数化方法[17, 29]进一步优化目标函数.该方法避免了直接去逼近精确模型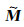
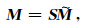
|
(19) |
其中, S为参数化算子, 其作用是抑制模型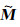

|
(20) |
考虑到精确模型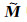
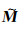
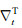
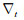
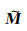
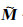

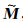
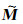
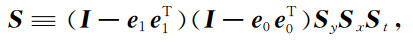
|
(21) |
式中, Sx、Sy和St分别表示沿主测线、联络测线和垂直方向的对称滤波算子; e0和e1表示M域内的两组归一化正交基, 即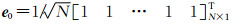
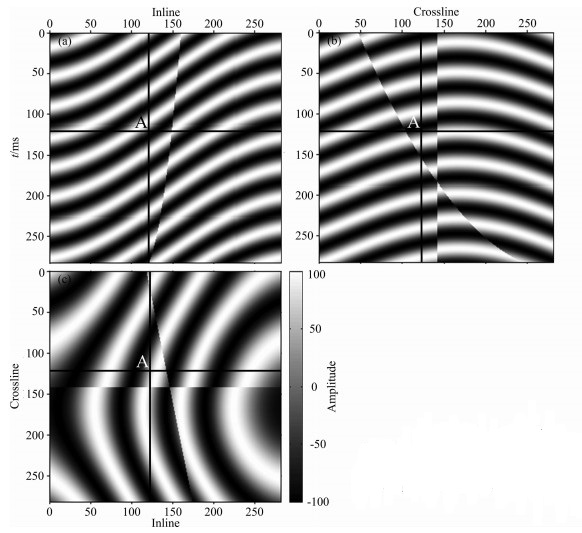
图 1为合成的三维模型数据体, (图 1a-图 1c)分别给出了沿主测线、联络测线和水平方向的三个剖面, 三个剖面互相垂直且相交于点A, 后面将点A作为参考点分析拉平变换前后点A所在同相轴的变化情况.从图中可见, 该模型中包含两个相交的断层, 其中一个为倾斜断层, 另一个为垂直断层; 在主测线和联络测线剖面内, 地震同相轴均呈现出弯曲变形, 使得很难从单一的水平时间切面中观察到完整的同相轴, 这在图 1c的水平切片中得到印证.
|
图 1 合成模型数据 (a)主测线;(b)联络测线;(c)时间切片 Fig. 1 Synthetic seismic data (a) Inline profile; (b) Crossline profile; (c) Time slice. |
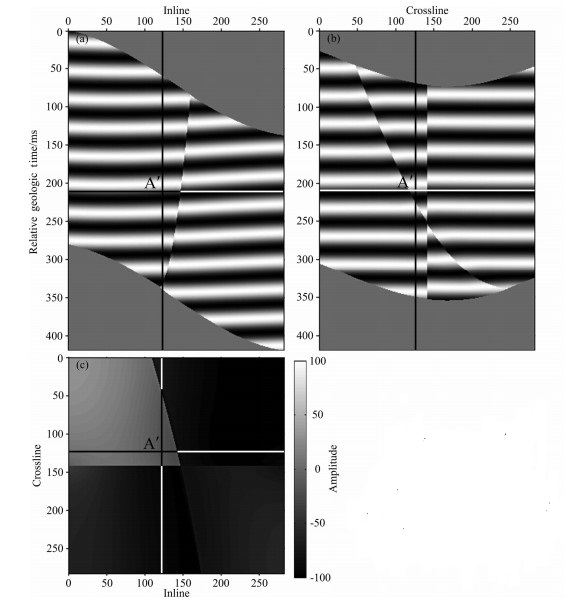
应用本文提出的全体积拉平方法处理该三维模型数据体.采用WVDF方法估算该模型数据体的局部地层倾角, 图 2为与图 1相对应的倾角数据的三个剖面.由于原始数据的断层两侧的地层倾角几乎没有变化, 从图 2可见, WVDF方法给出非常连续的倾角估算结果, 有效地避免了断层处出现大的倾角估计异常.以估算的局部地层倾角作为观测数据, 经过线性反演得到的拉平偏移量如图 3所示, 从三个互相垂直的剖面可以看出, 垂向偏移量在三维空间平缓变化, 具有非常好的光滑度, 保证拉平变换后数据的相对保真性; 图中垂向偏移量取正值表示采样点在拉平变换中垂直向上移动, 反之, 取负值表示垂直向下移动, 经过拉平变换后的三维数据体如图 4所示.在图 4中, 点A′为图 1中的参考点A经过拉平变换后对应的位置, 分析过点A ′的主测线、联络测剖面可见, 由断层分割开的地震同相轴分别以各自的基准线基本被拉平; 分析过点A ′的水平相对地质时间切片可见, 由两个相交断层分割的四个区域均呈现近似一致的振幅取值, 表明每个区域基本上只包含单一层位, 显示单一同相轴的变化情况, 其中左上角区域显示了图 1中参考点A所在的同相轴的情况.

|
图 2 基于WVDF方法计算合成数据的局部地层倾角 (a)主测线;(b)联络测线;(c)时间切片. Fig. 2 Local seismic slopes of synthetic data calculated by WVDF method (a) Inline profile; (b) Crossline profile; (c) Time slice. |

|
图 3 线性反演合成数据的拉平变换垂向偏移量 (a)主测线;(b)联络测线;(c)时间切片. Fig. 3 Flattening shifts of synthetic data calculated through the linear inversion algorithm (a) Inline profile; (b) Crossline profile; (c) Time slice. |
|
图 4 合成数据的全面积拉平变换结果 (a)主测线;(b)联络测线;(c)相对地质时间切片. Fig. 4 Volumetric flattening results of synthetic seismic data (a) Inline profile; (b) Crossline profile; (c) Relative geologic time slice. |
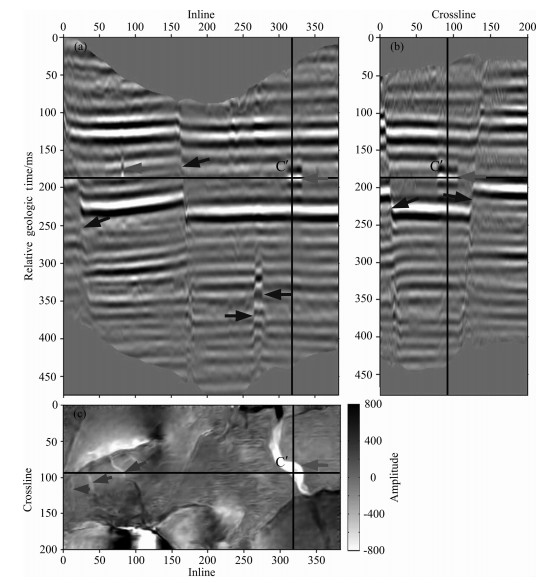
选择某油田的三维叠前时间偏移地震数据进行全体积拉平处理技术的实际应用, 该区块包含2 0 0条测线、4 0 0条联络测线, 时间范围为650~1050m s, 工区总面积约为32.0 km2. 图 5中给出该三维数据体分别沿主测线、联络测线和时间方向的三个剖面, 三个剖面互相垂直且相交于C点, 后面将以C点作为参考点分析拉平变换前后地震同相轴的变化情况.从图中可以看出, 该三维区块中的地震同相轴的形态特征较为复杂, 几处大断层、微小断裂(黑色箭头指示)以及若干明显的河道砂体沉积(灰色箭头指示)均造成同相轴的横向不连续性, 同时地质构造过程又引起地震同相轴发生较大的弯曲变形.对比分析两个垂直剖面与水平时间切片可见, 时间切片贯穿了多个地震同相轴, 也部分地横切了参考点C点所处的河道砂体沉积; 此外, 容易观察到该时间切面内河道砂体的反射波形出现多次明显的极性变化, 表明该时间切面横切了多个地质时间的河道砂体沉积, 这些均不利于对该河道砂体沉积的整体描述和沉积过程的分析.

|
图 5 XXX油田的三维地震数据体. (a)主测线;(b)联络测线;(c)时间切片. Fig. 5 3D field seismic data volume from XXX oil field. (a) Inline profile; (b) Crossline profile; (c) Time slice. |
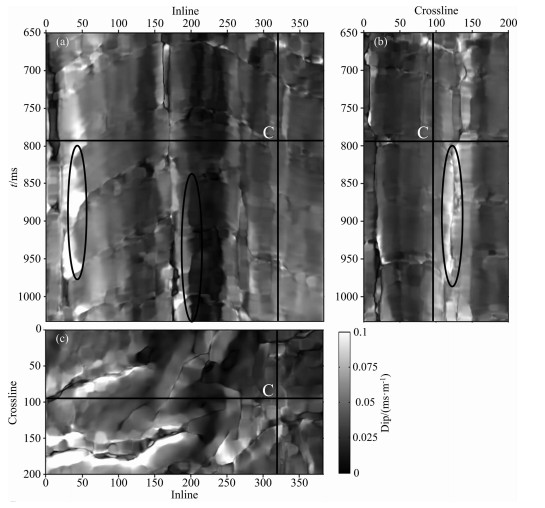
采用本文提出的全体积拉平方法处理该三维实际地震数据.采用WVDF方法估算的局部地层倾角数据如图 6所示, 三个互相垂直剖面的位置与图 5相对应.对比估算的倾角结果与图 5中的原始数据可见, 当地层倾角发生明显的变化时, 估算的倾角结果会体现出明显的倾角边界(圆圈框指示), 较为精确地反映出地层倾斜变化情况, 为拉平反演算法提供精确的观测数据.以该局部地层倾角作为观测数据, 经过线性反演得到的拉平偏移量如图 7所示, 经过拉平处理后的三维数据体如图 8所示.在图 8中, 点C′为图 5中的参考点C经过拉平变换后的对应位置, 分析过点C′的主测线、联络测线和水平方向的三个剖面可见, 断层的位置变得更为清晰, 断层两侧的地震同相轴在各自的区域内分别基本被拉平, 地震同相轴整体呈现为水平展布.相比图 5中原始数据的时间切片, 在图 8的相对地质时间切片内, 由断层所划分的局部区域内基本上只包含同一地质时间的沉积地层, 点C′所在河道沉积的反射波形的极性变化被消除, 从而能够更好地观察在特定地质时间内河道砂体沉积的空间展布特征; 此外, 左边区域内的一些细小的河道也在相对地质时间切片内得到清晰的显示.由此可见, 全体积拉平后的三维地震数据使得河道砂体等沉积特征得到更为清晰的显示, 有利于对河道砂体的识别和分析刻画.
|
图 6 基于WVDF方法计算实际地震数据的局部地层倾角. (a)主测线;(b)联络测线;(c)时间切片. Fig. 6 Local seismic slopes of field seismic data calculated by WVDF method (a) Inline profile; (b) Crossline profile; (c) Time slice. |

|
图 7 线性反演实际地震数据的拉平变换垂向偏移量 (a)主测线;(b)联络测线;(c)时间切片. Fig. 7 Flattening shifts of field seismic data calculated through the linear inversion algorithm (a) Inline profile; (b) Crossline profile; (c) Time slice. |
|
图 8 实际地震数据的全体积拉平变换结果 (a)主测线;(b)联络测线;(c)相对地质时间切片. Fig. 8 Volumetric flattening results of field seismic data (a) Inline profile; (b) Crossline profile; (c) Relative geologic time slice. |
三维地震数据的全体积拉平技术在地震层序解释以及地震地质建模等诸多方面都受到关注.针对含有断层等复杂地质构造的地震数据体的拉平处理, 本文提出一种基于高精度地层倾角的全体积拉平参数的线性反演方法.在估算局部地层倾角时, 采用精确度较高的WVDF方法, 为后继反演计算提供高质量的观测数据.在优化反演模型时, 通过在目标函数中引入误差模板和光滑度约束项, 抑制断层等复杂构造对反演效果的影响, 保证了拉平处理的相对保真性, 避免产生较大的波形畸变; 采用模型参数重新参数化方法构造合适的参数化算子, 不仅加快了反演计算的收敛速度, 也确保反演计算收敛于可行解.采用本文方法拉平处理三维合成模型和实际地震资料, 对比拉平前后相应位置的各个剖面, 可以看出拉平数据中同相轴都变为水平展布, 通过相对地质时间切片就可以观察到完整的同相轴, 有利于河道等沉积特征的刻画和识别.本文方法的一个不足之处是断层两侧的同相轴各自拉平, 导致无法将同一地震层位校准到同一相对地质时间位置, 如何将解释人员对断层两侧地震同相轴连接关系的先验理解引入到拉平模型中, 将是本文后继的研究内容.
| [1] | van Hoek T, Gesbert S, Pickens J. Geometric attributes for seismic stratigraphic interpretation. The Leading Edge , 2010, 29(9): 1056-1065. DOI:10.1190/1.3485766 |
| [2] | Hoyes J, Cheret T. A review of "global" interpretation methods for automated 3D horizon picking. The Leading Edge , 2011, 30(1): 38-47. DOI:10.1190/1.3535431 |
| [3] | Brouwer F, de Groot P, Kumpus M. Maximizing the value of seismic data through increased horizon mapping:applications in the Middle East and Canada. First Break , 2011, 29(3): 87-92. |
| [4] | Zeng H L, Backus M M, Barrow K T, et al. Stratal slicing, part I:realistic 3-D seismic model. Geophysics , 1998, 63(2): 502-513. DOI:10.1190/1.1444351 |
| [5] | Zeng H, Henry S C, Riola J P. Stratal slicing, Part Ⅱ:Real 3-D seismic data. Geophysics , 1998, 63(2): 514-522. DOI:10.1190/1.1444352 |
| [6] | Lee R F. Pitfalls in seismic data flattening. The Leading Edge , 2001, 20(2): 160-164. DOI:10.1190/1.1438896 |
| [7] | Stark T J. Unwrapping instantaneous phase to generate a Relative Geologic Time Volume.//73th Annual International Meeting, SEG. Expanded Abstracts, 2003. 1707-1710. |
| [8] | Stark T J. Relative geologic time (age) volumes-Relating every seismic sample to a geologically reasonable horizon. The Leading Edge , 2004, 23(9): 928-932. DOI:10.1190/1.1803505 |
| [9] | Pauget F, Lacaze S, Valding T. A global approach in seismic interpretation based on cost function minimization.//79th Annual International Meeting, SEG. Expanded Abstracts, 2009. 2592-2596. |
| [10] | de Groot P, de Bruin G, Hemstra N. How to create and use 3D wheeler transformed seismic volumes.//76th Annual International Meeting, SEG. Expanded Abstracts, 2006. 1038-1042. |
| [11] | de Groot P, Huck A, de Bruin G, et al. The horizon cube:A step change in seismic interpretation!. The Leading Edge , 2010, 29(9): 1048-1055. DOI:10.1190/1.3485765 |
| [12] | de Bruin G, Hemstra N, Pouwel A. Stratigraphic surfaces in the depositional and chronostratigraphic (Wheeler-transformed) domain. The Leading Edge , 2007, 26(7): 883-886. DOI:10.1190/1.2756868 |
| [13] | Wheeler H E. Time-stratigraphy. AAPG Bulletin , 1958, 42(5): 1047-1063. |
| [14] | Lomask J, Guitton A, Fomel S, et al. Flattening without picking. Geophysics , 2006, 71(4): 13-20. |
| [15] | Lomask J, Guitton A. Volumetric flattening:an interpretation tool. The Leading Edge , 2007, 26(7): 888-897. DOI:10.1190/1.2756869 |
| [16] | Fomel S. Predictive painting of 3D seismic volumes. Geophysics , 2010, 75(4): A25-A30. DOI:10.1190/1.3453847 |
| [17] | Parks D, Hale D. Seismic image flattening as a linear inverse problem. Colorado School of Mines, 2010 . |
| [18] | Ottolini R. Signal/noise separation in dip space. SEP report 37 , 1983: 143-149. |
| [19] | Fomel S. Applications of plane-wave destruction filters. Geophysics , 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [20] | 刘洋, 王典, 刘财, 等. 局部相关加权中值滤波技术及其在叠后随机噪声衰减中的应用. 地球物理学报 , 2011, 54(2): 358–367. Liu Y, Wang D, Liu C, et al. Weighted median filter based on local correlation and its application to poststack random noise attenuation. Chinese J. Geophys (in Chinese) , 2011, 54(2): 358-367. |
| [21] | Marfurt K J, Kirlin R L, Farmer S L, et al. 3-D seismic attributes using a semblance-base coherency algorithm. Geophysics , 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [22] | Marfurt K J, Sudhaker V, Gersztenkorn A, et al. Coherency calculations in the presence of structural dip. Geophysics , 1999, 64(1): 104-111. DOI:10.1190/1.1444508 |
| [23] | Fehmers G C, Hocker C F W. Fast structural interpretation with structure-oriented filtering. Geophysics , 2003, 68(4): 1286-1293. DOI:10.1190/1.1598121 |
| [24] | 杨培杰, 穆星, 张景涛. 方向性边界保持断层增强技术. 地球物理学报 , 2010, 23(12): 2992–2997. Yang P J, Mu X, Zhang J T. Orientational edge preserving fault enhance. Chinese J. Geophys. (in Chinese) , 2010, 23(12): 2992-2997. |
| [25] | Wang W, Gao J, Chen W. Robust estimates of seismic reflector orientations with weighted vector directional filter. Journal of Seismic Exploration , 2011, 20(2): 119-134. |
| [26] | Parks D, Harlan W, Hale D. Defining regions in seismic images by flattening. CWP-592 , 2008: 67-74. |
| [27] | Bakker P. Image structure analysis for seismic interpretation[Ph.D.thesis]. The Netherlands:Technische Universiteit Delft, 2002. http://www.sciencedirect.com/science/article/pii/S0040195101002505 |
| [28] | Golub G H, Van Loan C F. Matrix Computations. Baltimore & London: The Johns Hopkins University Press, 1996 . |
| [29] | Fomel S. Shaping regularization in geophysical-estimation problems. Geophysics , 2007, 72(2): R29-R36. DOI:10.1190/1.2433716 |
 2013, Vol. 56
2013, Vol. 56


