偏移是利用反射地震数据对地下构造进行成像的重要手段[1].但是常规的偏移方法采用的是正演算子的共轭转置[2], 而不是它的逆, 当地震数据采集不足且不规则, 地下构造情况复杂以及波场带宽有限时, 常规的偏移方法只能对地下构造模糊成像.针对这一问题, 许多地球物理学家开展了关于最小二乘偏移(LSM)方面的研究[3-9], 通过将成像看作最小二乘意义下的反演问题来得到压制偏移噪音后分辨率更高?振幅保真性更好的成像结果.
但是, LSM在工业界还没有得到推广应用, 究其原因主要在于两个方面:一是计算量太大, 如果将LSM看做数据空间的反演问题, 其计算量约为常规偏移的2×niter倍(niter为迭代次数), 虽然成像空间反演方式可以通过面向目标策略来提高计算速度, 但是当目标区域较大时, 存储成本(Hessian矩阵的存储)和计算成本仍然无法接受; 第二个阻碍因素是约束条件的选取, 合理的约束条件不仅可以保证反演过程稳定, 改善反演效果, 而且可以有效提高反演的收敛速度, 降低迭代次数, 从而也节约计算成本, 但是目前地球物理学家对于什么是LSM最优的约束条件仍然没有统一的结论.
自从将最小二乘反演理论引入到偏移成像以后[2-3], 关于LSM约束条件的研究就从未停止, 目前, 国内外文献中出现的约束条件主要有:(1)阻尼约束条件[3], 通过加入单位矩阵保证Hessian矩阵可逆, 该条件有效的前提是模型符合高斯分布, 但是反射系数往往是超高斯分布的, 因此该条件难以满足反射系数成像的要求; (2)共成像点道集的聚焦性或平滑性约束[4-6], 该条件是使得反演结果在共成像点道集上沿角度坐标平滑变化或聚焦在地下零偏移距; (3)倾角约束条件, 通过拾取反射波同相轴获得局部倾角信息, 利用该信息对反演结果进行约束[7-8], 该方法需要介入人工干预; (4)预测算子, 利用F-X预测滤波算子在共偏移距/角度道集对反演结果进行约束[9]; (5)去模糊化算子, 利用两次偏移结果估计出来的滤波器作为预条件算子提高反演的收敛速度[10-12]; (6)变换域稀疏约束, 利用成像结果在小波域或曲波域的稀疏分布特性进行约束, 使得反演结果变化更加连续自然[13].
与上述正则化方法不同, 本文在反演过程中同时引入两个正则化算子, 分别在共成像点道集上引入平滑算子, 在共偏移距道集上引入平面波构造滤波器算子.为了说明这两个算子对反演结果的影响, 利用Kirchhoff叠前时间偏移和反偏移算子在数据空间进行最小二乘偏移.通过理论模型和实际资料处理验证了本文方法可以同时压制共成像点道集和共偏移距道集上的成像噪音, 得到信噪比和精度更高的成像结果, 具有较好的应用效果和发展前景.
2 方法原理 2.1 Kirchhoff偏移/反偏移的基本原理在线性Born近似下, 地震波的传播过程可以用以下线性方程来描述[14] :
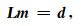
|
(1) |
其中, d表示叠前地震数据, m表示成像道集, L为从成像道集变换为地震数据的正演算子.L可以为波动方程或Kirchhoff反偏移算子.本文采用的是工业界常用的共偏移距道集Kirchhoff型积分算子作为正演算子L.此时, 二维情况下模型m为三维数据体, 三个维度分别为走时、成像点和偏移距.
为了更好地理解正演(反偏移)算子L, 首先考虑该算子的共轭算子LT——共偏移距道集叠前时间偏移, LT可以看做对输入数据进行加权叠加, 公式为
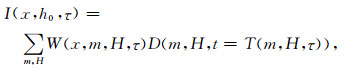
|
(2) |
其中x为中心点, h0为偏移距, τ为成像空间双程走时, m, H分别为数据空间的中心点和偏移距.实际上, H ∈ [h0-Δh, h0 +Δh], 其中Δh为偏移距面元大小. W为加权函数, 与成像点、炮点(s=m-H/ 2)和接收点(g=m +H/ 2)位置有关, D为输入地震数据.算法实现时, 对于给定的成像点(x, h0, τ), 计算偏移距面元内([h0-Δh, h0 +Δh])每个输入道对应的走时和加权函数, 并将加权后的数值加入模型数组中即可得到最终的成像结果.基于方程(2), 可以得到对应的反偏移算子:

|
(3) |
上式表明叠前数据同样可以通过对成像道集进行加权叠加得到.为了保证最小二乘反演迭代收敛, 所构建的偏移和反偏移算子必须是一对互为共轭的算子.为了保证其共轭性, 偏移和反偏移算子的加权函数必须相同, 可以通过点乘测试验证这对算子的共轭性[15].
2.2 LSM基本原理最小二乘偏移可以看作最小化以下目标函数的最优化反演问题:
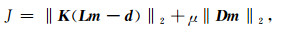
|
(4) |
其中‖r‖2为向量r的L2范数, K为掩码函数, 为对角矩阵, 存在数据地震道处为1, 缺道处为0, D为保证反演过程稳定而加入的正则化算子, μ为控制正则化程度的参数.当已知信息不足导致反演问题存在多解性时, 正则化算子所描述的约束条件非常重要.合理的正则化条件可以使得反演问题的解更快地向预期方向收敛.上式可以通过共轭梯度(CG)算法[16]进行求解.
为了加快CG算法的收敛速度, 引入预条件算子P=D-1, 并定义一个新的变量p, 满足以下关系:
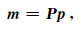
|
(5) |
目标函数变为:
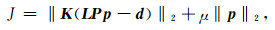
|
(6) |
同样, 可以利用共轭梯度法求取p, 代入式(5)即可得到最终的反演结果.
2.3 预条件算子的选取预条件算子的选取非常关键, 不仅可以保证反演过程稳定, 而且能够加快收敛速度, 本文将采用两个预条件算子分别沿模型的不同方向进行约束, 首先, 在共成像点道集(CIGs)上应用平滑算子Pcig进行约束, 使得反演结果沿偏移距方向平滑变化; 其次, 在每个共偏移距道集(COGs)上应用平面波构建算子(PWC)Ppwc沿局部倾角方向进行平滑约束.通过引入这两个算子可以从两个不同的方面对反演结果进行约束, 从而达到较好的反演效果, 下面分别介绍这两个算子的基本原理和实现过程.
CIGs平滑约束条件的合理性在于:当地表观测数据充足, 或者地下照明充分时, CIGs的能量将沿横向坐标平滑变化.因此, 根据这一特点, 可以在CIGs引入平滑算子对反演结果进行约束.一般采用一阶差分正则化算子作为高通滤波器压制沿偏移距方向变化的高频信息.一阶差分算子的逆为因果积分算子, 而预条件算子和正则化算子互逆, 因此预条件算子为因果积分算子, 为了使得反演结果振幅变化更加均衡, 对因果积分算子进行改进, 加入积分次数作为除数.CIGs平滑算子Pcig定义为以下矩阵的形式:
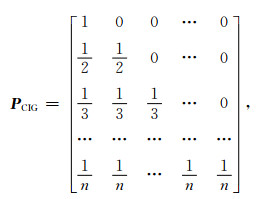
|
(7) |
上式的数学物理意义为:在CIGs上沿偏移距/角度方向对成像结果进行平滑处理, 消除不规则数据对叠前道集的影响, 改善成像效果.
除了在CIGs引入平滑约束条件外, 本文还采用了PWC算子[17]在COGs进行约束, 其基本思想是使得反演结果沿所预测的局部倾角方向平滑变化.所采用的PWC算子是平面波解构滤波器(PWD)算子[18]的逆.假定地震剖面s由一系列地震道组成, s=[s1 s2…sN]T. PWD算子根据相邻道预测该道数据, 并将原始道与预测道相减, 数学表达式为:
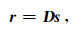
|
(8) |
其中r为剩余量, D为PWD算子, 定义为:
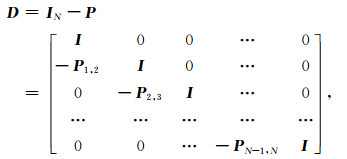
|
(9) |
其中I为单位算子, P为预测算子, 通过沿同相轴倾角方向移动原始道来预测下一道地震数据, Pi, j表示由第i道预测第j道的算子.式(8)可以通过正则化共轭梯度法最小化预测误差r估计出主要的局部倾角信息.该反演问题的约束条件通常是使得数据空间倾角平滑变化[19].
PWC算子是PWD算子的逆, 通过矩阵运算, 对PWC算子进行推导, 推导过程如下:

|
(10) |
为了提高计算效率, 可以采用递归算法实现PWC算子, 以下方程:
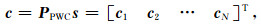
|
(11) |
的递归求解公式为:
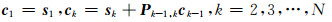
|
(12) |
结合这两个预条件算子, 原目标函数(6)变为:
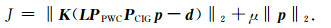
|
(13) |
随着迭代次数的增加, 预条件共轭梯度法使得反演结果由简单到复杂变化[20], 迭代过程同样起着控制约束条件强度的作用, 因此可以取μ=0, 这样通过设置迭代次数就可以达到控制预条件化强度的目的, 从而少了一个人为控制变量.通过迭代得到最优的向量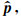
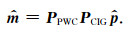
|
(14) |
采用共轭梯度法对目标函数(13)进行求解, 具体求解过程为:(1)初始化, 令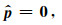
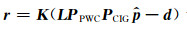
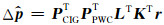
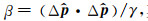
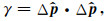
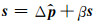

为了验证本文所提出的LSM约束条件的正确性和有效性, 分别对凹陷模型和实际资料进行成像处理, 对比常规偏移、CIGs平滑约束LSM、CIGs平滑约束和COGs局部倾角约束LSM三种方法的成像效果.
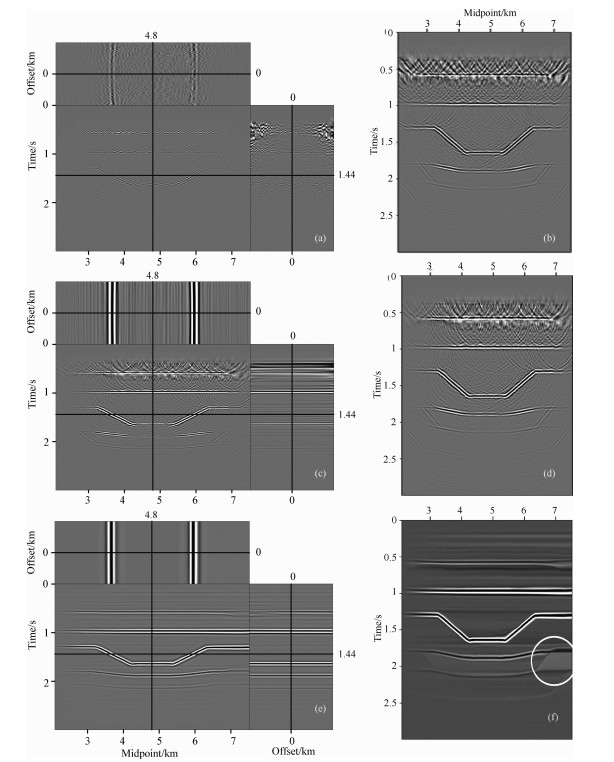
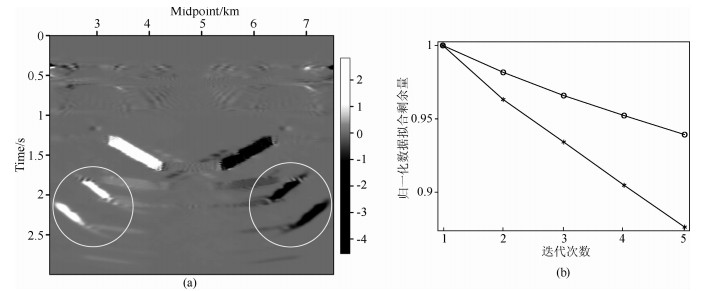
3.1 凹陷模型测试首先采用凹陷模型进行测试, 该模型层速度场如图 1a所示, 图 1b为有限差分正演合成的叠前数据(切除直达波). 图 1c为由Dix公式转化而来的均方根速度场, 图 1d为随机抽取70%地震道后的数据, 对该数据进行常规Kirchhoff叠前时间偏移, 叠前成像道集如图 2b所示, 从图中可以看出, 受不规则数据的影响, 常规偏移的CIGs和COGs都受噪音影响严重, 图 2b为沿共成像点道集叠加后的成像结果, 从图中可以看出, 通过叠加可以在一定程度上压制不规则数据产生的偏移噪音, 凹陷构造得到比较准确的成像, 但是信噪比仍然很低.为了压制噪音, 采用LSM进行成像, 图 2c为CIGs平滑约束条件下进行最小二乘偏移的成像结果, 迭代次数为5次, 从图中可以看出, CIGs剖面上的噪音得到有效压制, 但是COGs仍然存在较强的噪音. 图 2d为所有CIGs叠加后的成像结果, 从图中可以看出, 相对于常规偏移, CIGs平滑约束LSM叠加后的成像结果并没有得到多少改善, 其原因在于将所有CIGs叠加同样起着平滑的作用, CIGs平滑约束条件的作用不明显.为了进一步改善成像效果, 采用PWC算子在COGs进行约束, 使得反演结果在COGs道集上沿预测的局部倾角平滑变化.该方法首先采用PWD对常规偏移结果(图 2b所示)估计局部倾角, 如图 3a所示, 从图中可以看出, 局部倾角场基本反映了主要反射同相轴的信息, 但是圆圈所示倾角为多次波没有正确归位所导致的假同相轴信息, 该倾角信息会在一定程度上影响PWC预条件算子的应用效果.利用估计出来的局部倾角信息构建PWC算子后, 在COGs进行预条件化, 图 2e为CIGs平滑约束和COGs局部倾角约束共同作用后的最小二乘反演结果, 同样只迭代5次, 从图中可以看出, 通过引入这两个预条件算子之后, 不仅压制了共成像点道集上的成像噪音, 共偏移距道集上的噪音也得到有效压制. 图 2f为所有CIGs叠加后的反演成像结果, 从图中可以看出, 引入COGs局部倾角约束条件可以较大程度上改善最终的叠加成像质量, 有效压制成像噪音.但是由于局部倾角信息中存在错误的多次波成像信息, COGs局部倾角约束后反演结果会受到一定的影响, 如图 2f中圆圈所示, 可以通过前期处理去除多次波来解决这一问题. 图 3b分别为CIGs平滑约束条件LSM和CIGs平滑约束条件加COGs局部倾角约束条件LSM的归一化数据拟合剩余量随迭代次数的变化曲线, 由于本文的重点是介绍一种新的预条件算子PWC, 所采用的正演算子比较简单, 而且迭代次数有限, 因此归一化数据拟合剩余量没有收敛到较低的值, 但是随着迭代次数的增加, 归一化数据拟合剩余量逐渐减小.并且对比这两条曲线可以看出, 通过加合适的预条件算子, 可以有效加快收敛速度.
|
图 1 速度模型及正演数据 (a)模型层速度场; (b)有限差分正演数据; (c)均方根速度场; (d)随机抽除70%后的数据体. Fig. 1 Velocity field and modeling data (a)Interval velocity field; (b)Finite difference modeling data; (c)RMS velocity field; (d)Seismic data after 70% removed randomly. |
|
图 2 对比常规偏移、平滑约束反演、平滑约束和局部倾角约束反演的成像结果 (a)Kirchhoff偏移成像道集; (b)Kirchhoff偏移叠加成像结果; (c)CIGs平滑约束LSM成像道集; (d)CIGs平滑约束LSM叠加成像结果; (e)CIGs平滑和COGs局部倾角约束LSM成像道集; (f)CIGs平滑和COGs局部倾角约束LSM叠加成像结果. Fig. 2 Comparison of images of conventional migration, CIGs smoothing constrained LSM, CIGs smoothing and COGs local slope constrained LSM (a)Image gathers of Kirchhoff migration; (b)The stacked image of Kirchhoff migration; (c)Image gathers of CIGs smoothing constrained LSM; (d)The stacked image of CIGs smoothing constrained LSM; (e)Image gathers of CIGs smoothing and COGslocal slope constrained LSM; (f)The stacked image of CIGs smoothing and COGs local slope constrained LSM. |
|
图 3 局部倾角和归一化数据拟合剩余量随迭代次数的变化曲线 (a)局部倾角场; (b)归一化数据拟合剩余量随迭代次数的变化曲线.-o-为cigs平滑约束LSM; -*-为cigs平滑约束和COGs局部倾角约束LSM. Fig. 3 Local slope field and data misfit curve for CIGs smoothing constrained(-o-) and CIGs smoothing & COGs local slope constrained(-*-) LSM (a) Local slope field; (b) Data misfit curve for CIGs smoothing constrained and CIGs. |
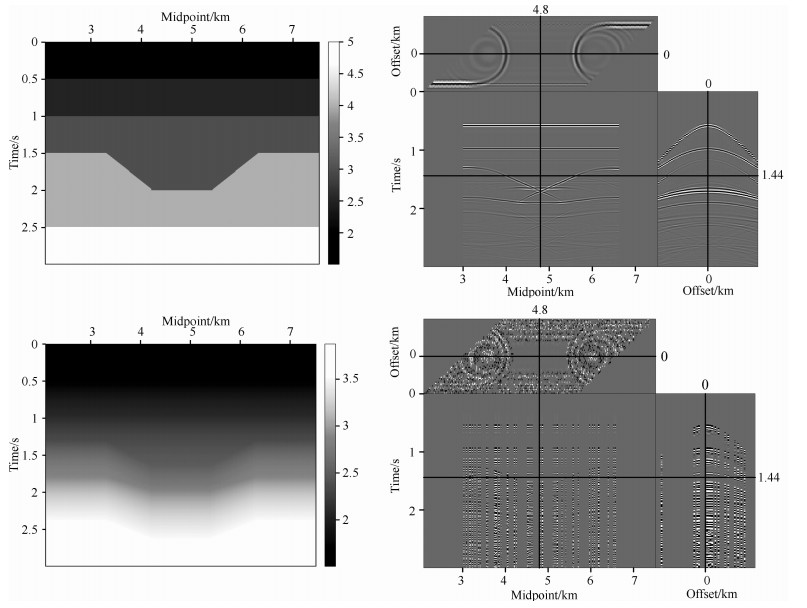
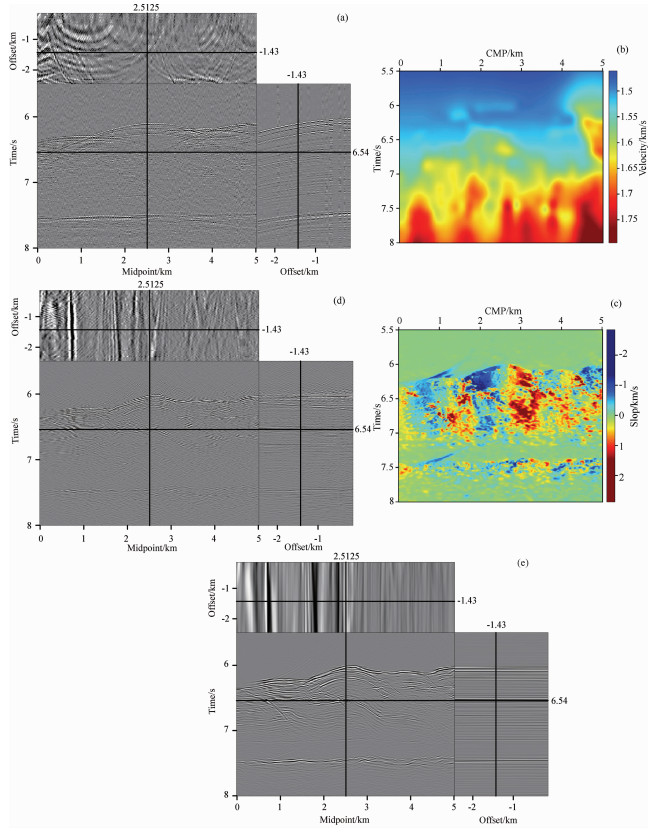
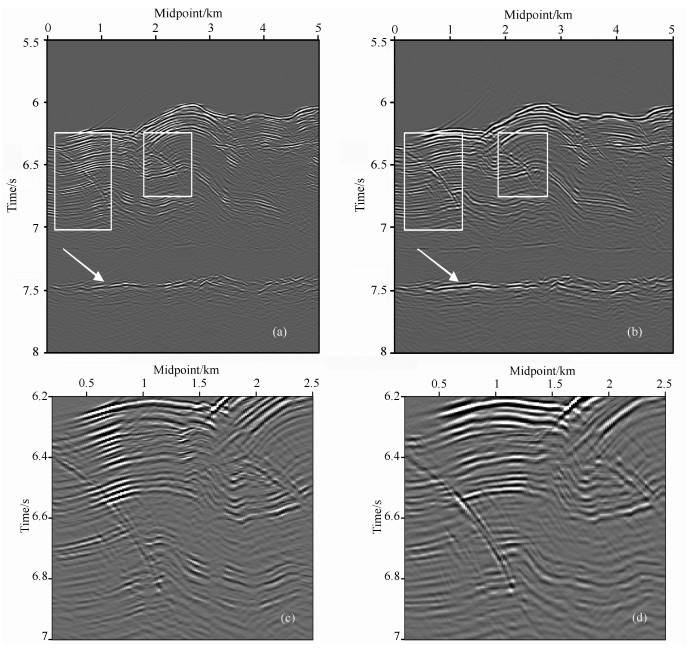
为了进一步说明本文方法的有效性, 下面对深海地震数据进行成像处理, 图 4a为面元归一化后的叠前数据, 从图中可以看出, 该数据体存在明显的数据缺失和不规则现象. 图 4b为叠加速度分析得到的均方根速度场, 图 4d为利用该速度场进行常规Kirchhoff偏移的成像结果, 从图中可以看出, 受数据缺失和不规则性的影响, 共成像点道集和共偏移距道集上噪音严重.采用PWD对常规偏移叠加成像结果进行局部倾角估计, 估计的局部倾角场如图 4c所示. 图 4e为CIGs平滑约束和COGs局部倾角约束的LSM反演结果, 迭代次数为5次, 从图中可以看出, 成像道集和共偏移距道集上的噪音得到有效压制, 成像质量得到有效提高.分别对常规偏移和LSM的所有共成像点道集进行叠加, 得到叠加成像结果, 如图 5a、图 5b所示, 从图中可以看出, 加入本文的正则化约束条件后的LSM成像结果不仅具有更高的信噪比, 而且具有更高的成像精度, 尤其是方框所标定位置处, LSM对断层的刻画更加清晰, 对箭头所示地层的反射波振幅也得到一定的恢复. 图 5c、图 5d分别为常规偏移和LSM叠加成像结果的局部放大图, 从图中可以进一步看出, LSM对局部地区的刻画更加清晰, 具有更高的成像精度.
|
图 4 常规偏移和LSM叠加成像结果比较. (a)面元归一化后的数据体; (b)叠加速度分析得到的均方根速度场; (c)局部倾角场; (d)Kirchhoff偏移结果; (e)LSM成像结果 Fig. 4 Comparison of image gathers of conventional migration and LSM. (a) Data cube after normalized binning; (b) RMS velocity field after stack velocity analysis; (c) Local slope field; (d) Image gathers of Kirchhoff migraion; (e) Image gathers of LSM |
|
图 5 常规偏移和LSM叠加成像结果比较 (a)常规偏移的叠加成像结果; (b)LSM的叠加成像结果; (c)常规偏移成像结果局部放大; (d)LSM成像结果局部放大. Fig. 5 Comparison of stacked image of conventional migration and LSM (a) Stacked image of conventional migration; (b) Stacked image of LSM; (c) Close up of conventional migration image; (d) Close up of LSM image. |
本文采用Kirchhoff叠前时间偏移和反偏移算子进行最小二乘反演成像, 并引入CIGs平滑约束条件和COGs局部倾角约束条件改善反演效果, 通过模型和实际资料处理, 对比常规偏移和不同约束条件下LSM的成像结果, 可以得出如下几点结论:
(1)本文方法的关键之一是偏移与反偏移算子的构建, 这对算子必须互为共轭才能保证迭代反演过程收敛; (2)CIGs平滑约束条件可以有效压制CIGs上的成像噪音, 使得反演后道集内振幅沿偏移距平滑变化, 但是对最终的叠加成像结果没有多少改善; (3)同时加入CIGs平滑约束条件和COGs局部倾角约束条件, 可以从两个不同的方向对反演结果进行优化, 压制CIGs和COGs上的偏移噪音, 并且能够改善最终的反演效果, 提高成像精度; (4)通过加入合适的预条件算子, 可以有效提高反演的收敛速度, 从而在一定程度上降低LSM的计算成本.
虽然本文提出的局部倾角约束条件在模型试算和实际资料处理中都具有一定的应用效果, 但是仍然存在一些需要改进的地方, 比如:(1)局部倾角约束条件有效的前提是局部倾角估算准确, 当地震数据本身信噪比较低时, PWD往往难以正确估算出有效反射层的局部倾角信息, 不准确的先验信息将对LSM结果产生负面影响, 因此今后将进一步开展PWD方面的研究, 使得PWD能够更好地适用于低信噪比数据; (2)本文主要论述局部倾角约束条件在LSM中的应用, 所采用的偏移和反偏移算子比较简单, 事实上, 该约束条件同样适用于深度域LSM, 采用复杂的偏移和反偏移算子更有利于高精度成像, 因此下一步将开展深度域LSM的研究; (3)本文主要讨论了LSM对不规则数据成像的优势, 除此之外, 相对于常规偏移, LSM还可以提高成像的分辨率、改善成像的振幅保真度, 因此下一步的工作将集中在LSM的成像分辨率分析和保真度评价上.
致谢作者感谢两位匿名审稿人的宝贵意见.感谢Madagascar为本文的绘图提供的支持(Fomel & Sava 2006).
| [1] | Claerbout J F. Towards a unified theory of reflector mapping. Geophysics , 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [2] | Lailly P. The seismic inverse problem as a sequence of before stack migration.//Bednar J ed. Conference on Inverse Scattering:Theory and Applications, SIAM, Expanded Abstracts, 1983:206-220. |
| [3] | Tarantola A. Inversion of seismic reflection data in the acoustic approximation. Geophysics , 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [4] | Kuehl H, Sacchi W D. Least-squares wave-equation migration for AVP/AVA inversion. Geophysics , 2003, 68(1): 262-273. DOI:10.1190/1.1543212 |
| [5] | Clapp M L. Imaging under salt:Illumination compensation by regularized inversion. Stanford: Stanford Univ, 2005 . |
| [6] | Valenciano A A, Biondi B, Guitton A. Target-oriented wave-equation inversion. Geophysics , 2006, 71(4): A35-A38. DOI:10.1190/1.2213359 |
| [7] | Prucha M, Biondi B. Subsalt event regularization with steering filters.//72nd Annual International Meeting, SEG, Expanded Abstracts, 2002:824-827. |
| [8] | Tang Y X. Target-oriented wave-equation least-squares migration/inversion with phase-encoded Hessian. Geophysics , 2009, 74(6): WCA95-WCA107. DOI:10.1190/1.3204768 |
| [9] | Wang J, Sacchi M D. Structure constrained least-squares migration.//79th Ann. Internat Mtg., Soc. Expl. Geophys. Expanded Abstracts, 2009:2763-2767. |
| [10] | Symes W W. Approximate linearized inversion by optimal scaling of prestack depth migration. Geophysics , 2008, 73(2): R23-R35. DOI:10.1190/1.2836323 |
| [11] | Rickett J E. Illumination-based normalization for wave-equation depth migration. Geophysics , 2003, 68(4): 1371-1379. DOI:10.1190/1.1598130 |
| [12] | Aoki N, Schuster G T. Fast least-squares migration with a deblurring filter. Geophysics , 2009, 74(6): WCA83-WCA93. DOI:10.1190/1.3155162 |
| [13] | Herrmann F J, Brown C R, Erlangga Y A, et al. Curvelet-based migration preconditioning and scaling. Geophysics , 2009, 74(4): A41-A46. DOI:10.1190/1.3124753 |
| [14] | Stolt R H, Benson A. Seismic Migration:Theory and Practice. Amsterdam: Geophysical Press, 1986 . |
| [15] | Claerbout J F. Earth Soundings Analysis-Processing Versus Inversion. Blackwell Scientific Publications, 1992 . |
| [16] | Hestenes M, Steifel E. Methods of conjugate gradients for solving linear systems. Journal of Research of the National Institute of Standards , 1952, 49(6): 409-436. DOI:10.6028/jres.049.044 |
| [17] | Fomel S B, Guitton A. Regularizing seismic inverse problems by model reparameterization using plane-wave construction. Geophysics , 2006, 71(5): A43-A47. DOI:10.1190/1.2335609 |
| [18] | Fomel S B. Applications of plane-wave destruction filters. Geophysics , 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [19] | Fomel S B. Shaping regularization in geophysical estimation problems.//75th Annual International Meeting, SEG Expanded Abstracts, 2005:1673-1676. http://www.oalib.com/references/19003773 |
| [20] | Fomel S B. Three Dimension Seismic Data Regularization. Stanford: Stanford Univ, 2001 . |
 2013, Vol. 56
2013, Vol. 56

