2. 中国石油大学(北京)CNPC物探重点实验室, 北京 102249
2. CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum, Beijing 102249, China
始于20世纪80年代的逆时偏移技术, 由于其在理论上能对无论来自多么复杂路径的信号, 都让它们复原归位, 能够对复杂的地下构造做出精确的成像, 所以被认为是现行偏移方法中最为准确的成像方法之一.逆时偏移是一种基于波动理论的直接求解波动方程的深度域偏移方法.常用的求解波动方程的方法有有限差分法、有限元、伪谱法等.逆时偏移思想的最早起源是用有限差分法求解波动方程实现的[1], 而后其他学者将逆时偏移开始真正引入地震勘探领域:Baysal等[2]采用伪谱法实现了逆时偏移; McMechan[3]采用时间和空间域二阶精度有限差分法求解全声波方程实现了逆时偏移; Loewenthal和Mufti[4]在频率波数域利用指数解析解求解波动方程实现逆时偏移.上述这些方法最初都是用于叠后偏移.Chang和McMechan[5-9]先后采用有限差分实现了声波、弹性波的叠前逆时偏移; Wu等[10]分析了高阶有限差分叠前逆时偏移的成像精度; Yoon等[11]分别采用声波波动方程高阶有限差分和伪谱法实现了三维叠前逆时偏移成像; Xu等[12]利用频率域外推实现了叠前逆时偏移; Duveneck等[13]和Zhang等[14]分别用有限差分实现了各向异性声波方程叠前逆时偏移; Neto等[15]提出了2.5D有限差分叠前逆时偏移方法.在国内, 对逆时偏移的研究要相对晚一些.底青云等[16]开展了弹性波有限元逆时偏移技术研究; 张会星、何兵寿、杜启振、刘红伟等[17-21]先后利用高阶有限差分实现了标量波场和矢量波场的叠前逆时偏移; 王童奎等[22]用谱元法求解波动方程实现叠前逆时偏移; 刘伊克等[23]提出了利用地震多次波进行逆时偏移的成像新方法, 该方法能对盐丘下部更好地成像, 为地震成像的研究开拓了一个新的研究方向.另外, 在逆时偏移的成像条件、计算效率、存储及去噪等方面, 一些学者进行了专门的研究:如Chattopadhyay和McMechan[24]对几种成像条件进行了对比分析; 李博等[25]针对计算量大的问题, 提出了CUP/GPU对策; Zhang等[26]提出利用拉普拉斯算子滤波方法压制低频偏移噪声; 刘红伟等[27]分析和总结了几种存储和去噪方法.
叠前逆时偏移实现过程中的主要步骤是波场的正向延拓和反向延拓、成像条件以及成像后的低频噪声的消除, 其中, 波场正向延拓和反向延拓的本质就是求解波动方程.求解波动方程是为了描述地震波场的传播特征, 理论上利用全波场的信息对地下构造进行准确成像, 所以精确、快速地求解波动方程至关重要.Karazincir和Gerrard[28]实现并比较了伪谱法和高阶有限差分法求解波动方程的逆时偏移, 认为高阶有限差分法的计算效率更高, 还不存在傅里叶变换所产生的噪声, 且灵活易实现, 所以采用有限差分法实现叠前逆时偏移是相对应用最为广泛的.
然而, 常规的有限差分法求解波动方程时, 其求空间导数时的差分系数一般都是采用传统的高阶有限差分系数[29], 该系数是由空间导数项的Taylor级数展开式而推导出的, 其只与空间域有关, 而实际计算地震波场的传播还与时间域有关, 所以采用常规有限差分系数求解方程时, 就会存在较大的频散和误差.Liu和Sen[30]同时考虑声波方程的时间和空间导数, 以平面波理论和Taylor级数展开为基础, 基于时空域频散关系, 推导出一种新的有限差分系数, 其求解方程的精度更高、稳定性更好.我们将此精度更高的差分方法发展到声波叠前逆时偏移的波场延拓中, 采用基于时空域频散关系的有限差分系数[30]求解方程, 分析其数频散和稳定性, 并与传统有限差分进行了对比.在叠前逆时偏移的正向延拓和反向延拓过程中, 采用此时空域高阶有限差分法求解方程, 以提高成像精度.求解方程时, 还采用自适应变长度的空间差分算子求解空间导数的有限差分策略提高计算效率[31], 利用归一化互相关成像条件进行成像, 采用拉普拉斯算子去除低频噪声, 以得到最后的成像剖面.
2 方法原理 2.1 时空域有限差分逆时偏移的核心问题之一是求解波动方程.在纵波勘探中, 一般采用声波方程近似描述地震波在地下介质中的传播, 二维声波方程为
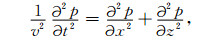
|
(1) |
其中, p为标量波场, v为速度, t为时间, x、z为空间坐标.
一般情况下, 计算时间二阶导数时, 如果采用高阶精度差分形式, 则计算量会很大, 并且很容易造成不稳定[32], 所以一般采用二阶中心差分形式:
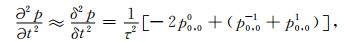
|
(2) |
其中, τ为时间采样间隔, pm, jn=p(x+mh, z+jh, t+nτ).
方程(1)中空间二阶导数的2M阶精度差分形式可以写为
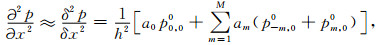
|
(3a) |
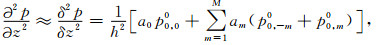
|
(3b) |
其中, am为差分系数, h为空间采样间隔.
将式(2)和式(3)代入声波方程(1)中, 可以得到:
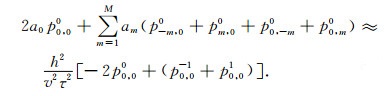
|
(4) |
逆时偏移的正向延拓就是差分方程正演模拟的过程, 由式(4)可以推导出正向延拓的表达式:
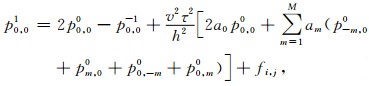
|
(5) |
其中, fi, j是震源项.
逆时偏移波场的反向延拓过程就是已知后一时刻的波场值来求前一时刻的波场值, 具体计算过程与正向延拓类似, 其计算表达式为
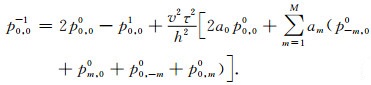
|
(6) |
Liu和Sen[30]根据平面波理论, 将一平面简谐波代入(4)式中, 进行推导得到:
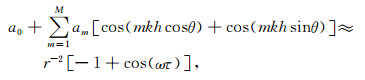
|
(7) |
其中, 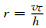
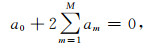
|
(8) |
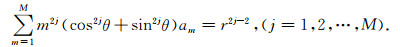
|
(9) |
令f(θ)=cos2jθ+sin2jθ, 则有f(θ)=f(nπ/2±θ).一般情况下, 把θ=π/8代入式(9), 然后求解差分系数, 则在8个方向上θ=(2n-1)π/8, (n=1, 2, …, 8), 有限差分求解可以达到2M阶精度[30].
为了计算和分析基于时空域有限差分的计算精度, 我们分析差分的频散, 由式(7)定义频散速度vFD为
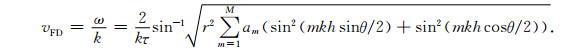
|
(10) |
用频散速度与真实速度的比值来衡量二维声波方程的频散现象, 则可以得到二维声波方程的频散分析表达式[30]:
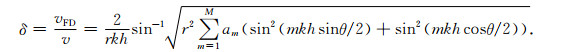
|
(11) |
由于δ(θ)=δ(θ+π/2), 所以δ(θ)是一个以π/2为周期的函数.同时考虑到δ(θ)=δ(π/2-θ), 所以在计算δ(θ)时, θ的变化是从0到π/4.从式(11)中可以看出, 如果δ=1, 则模拟时不存在数值频散, 如果δ越是偏离1, 则存在越大的数值频散.
由式(7)变形可得到:

|
(12) |
从式(12)可以看出, 由于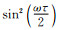
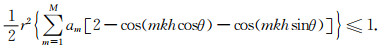
|
(13) |
由于am值以正负交替出现, 因此当kcosθ=ksinθ=π/h时, 式(13)的左端取最大值.所以(13)式可以化简为[30]
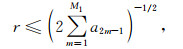
|
(14) |
其中M1为不超过M的最大奇数.
设计一个具体模型进行精度分析:介质的速度为3000m/s, 模型网格大小为10m×10m, 时间步长为0.001s, 空间导数精度阶数2M分别为4、8、16、32.图 1(a, b)是波在传播方向θ=π/8上, 分别采用传统有限差分和时空域有限差分数值模拟时的频散分析曲线图.从图 1中可以看出:在相同参数情况下, 时空域有限差分的频散程度比传统有限差分的频散程度要小, 即时空域有限差分的模拟精度要高于传统有限差分[30].
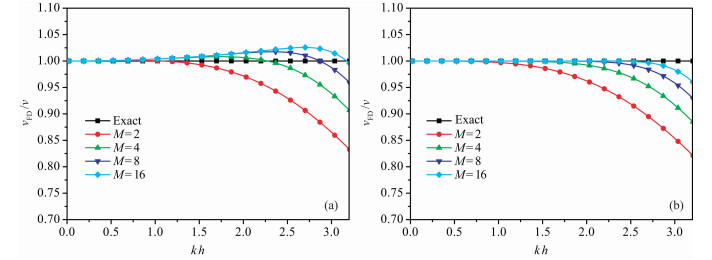
|
图 1 声波方程有限差分采用不同的差分算子长度数值模拟时频散分析曲线图 (a)传统有限差分;(b)时空域有限差分. Fig. 1 Plot of dispersion curvesof the conventional and time-space domain FD methods in the acoustic medium for different space point numbers (a) The conventional FD method; (b) The tme-space domain FD method. |
如果空间导数的精度阶数2M固定为16, 而波的传播角度θ分别取0、π/16、2π/16、3π/16、4π/16, 其按顺序对应的标识为angle1、angle2、angle3、angle4、angle5.图 2是有限差分数值模拟在不同方向上频散分析曲线图.从图 2(a, b)的频散分析曲线图对比也可以看出:在精度阶数相同时, 在波的各个传播方向上, 时空域有限差分的模拟精度比传统有限差分高[30].
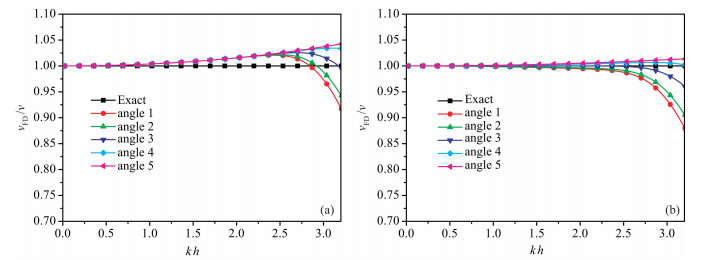
|
图 2 声波方程有限差分数值模拟在不同传播方向上频散分析曲线图 (a)传统有限差分;(b)时空域有限差分. Fig. 2 Plot of dispersion curves of the cosvestiosal and time-space domain FD methods for different propagation angles is the acoustic medium (a) The conventional FD method; (b) The time-space domain FD method. |
为比较传统有限差分和基于时空域有限差分的稳定性, 由式(12)可令稳定因子s为
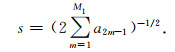
|
(15) |
图 3是声波方程有限差分在不同的精度阶数(M分别为2、4、8、16)时随数值模拟参数变化的稳定性分析曲线图.从图 3中可以看到, 当精度阶数越高时, 越容易造成不稳定, 且时空域有限差分的稳定因子与精度阶数2M和数值模拟参数r有关, 而传统有限差分的稳定因子s只与精度阶数2M有关, 同时对比两类差分的稳定性分析图, 可以看到, 在保持求解方程稳定的前提下(s≥r), 时空域的有限差分对应的r可取更大更广的范围.所以图 3中表明, 时空域的有限差分的稳性比传统有限差分的稳定性更好[30].
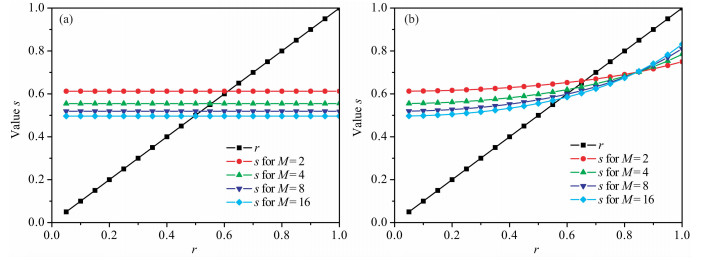
|
图 3 声波方程有限差分在不同的精度阶数时随数值模拟参数变化的稳定性分析曲线图 (a)传统有限差分;(b)时空域有限差分. Fig. 3 Plot of stability conditions for the cosvestiosal and tme-space domain FD methods is the acoustic medium (a) The conventional FD method; (b) The tme-space domain FD method. |
在给定一个地质模型后, 采用高阶有限差分进行数值模拟时, 通常都是采用固定长度的空间差分算子来计算空间导数.差分算子长度的选择必须同时满足稳定性、精度、计算量等的要求, 而这些需要满足的要求又与介质模型的速度有关.对于给定的速度模型, 如果整体采用一个固定长度的空间差分算子来进行数值模拟, 则这个固定的空间差分算子必须同时满足模型中所有速度各自应该满足的条件.因此, 固定的空间差分算子长度一般会要求比较长, 导致求解波动方程耗费大量计算时间.Liu和Sen[31]提出采用自适应差分变算子长度求解空间导数, 即在速度小的网格用长的空间差分算子, 速度大的网格用短的空间差分算子, 在保证精度要求的前提下, 节省求解波动方程时所需的内存和提高求解波动方程的计算效率.将此策略应用到叠前逆时偏移求解方程的正向延拓和反向延拓中, 可以提高计算效率.
求取自适应差分算子长度时, 先定义有限差分数值模拟的误差计算公式[31]:
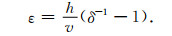
|
(16) |
给定最大频率fmax和最大误差η后, 则要满足不等式[31]:
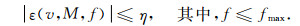
|
(17) |
设计一个速度范围为1500~5500m/s, 网格大小为10m×10 m, 时间步长为0.001s, 其最大频率为50Hz, 而计算误差范围分别控制在10-4、10-5、10-6、10-7时的差分算子长度.图 4为计算得到的不同速度对应的差分算子长度.从图 4中可以看出: ①在不超过一定的误差范围内, 速度越低, 所要求的差分算子长度越长, 即低速体要求的差分算子长度比高速体要求的差分算子长度要长; ②误差要求越小, 即精度要求越高时, 所要求的差分算子长度越长[31].

|
图 4 不同的速度和误差控制所对应的差分算子长度 Fig. 4 Plot of FD operator lengths for different velocities and maximum errors |
成像条件也是逆时偏移处理过程中的一个重要步骤, 成像条件的好坏直接影响着最终成像剖面的质量.目前叠前逆时偏移中常用的成像条件主要有三种类型:激发时间成像条件[33]、上下行波振幅比成像条件[24]和互相关成像条件[34].Chattopadhyay和McMechan [24]对这几种成像条件进行了分析, 认为震源归一化互相关的成像振幅能够反映模型的反射系数, 且成像信息位置正确.本文采用震源归一化相关成像条件进行成像, 其表达式为
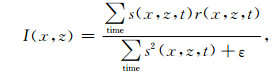
|
(18) |
其中, I(x, z)是点(x, z)的成像结果; s(x, z, t)表示时间域的正向延拓波场; r(x, z, ω)表示时间域的反向延拓波场; ε为无穷小实数, 其作用是为了保证计算的稳定性.
由于时间域计算相互关的速度相对比较慢, 为了提高其计算效率, 本文在实现过程中将波场转换到频率域计算互相关, 式(16)可以转换为
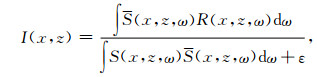
|
(19) |
其中, ω表示角频率, S(x, z, ω)表示频率域的正向延拓波场, R(x, z, ω)表示频率域的反向延拓波场, 珚S(x, z, ω)表示S(x, z, ω)的共轭.
2.4 拉普拉斯算子去噪叠前逆时偏移的过程中, 不可避免地会产生低频噪声, 所以要得到最终的清晰成像结果, 还要对偏移的初始剖面进行去噪处理.拉普拉斯算子去噪方法简单且易操作, 一般将其写成二阶差分形式, 对逆时偏移成像结果进行滤波, 对低频噪声去除效果比较明显[26].在本文中采用拉普拉斯算子去噪方法对二维逆时偏移的结果进行滤波处理.
拉普拉斯算子表达式为
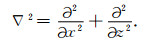
|
(20) |
其在波数域表示为
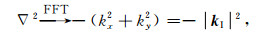
|
(21) |
其中, kI是成像域波数矢量, 且存在如下关系式[35]:
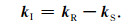
|
(22) |
应用余弦定理, 由波数域矢量计算方法可以得到:
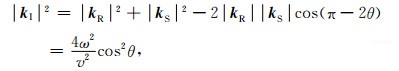
|
(23) |
式(20)中θ是入射角, kR和kS分别是接收点波场与震源波场的波数矢量.从此式可以看出:对逆时偏移结果进行拉普拉斯算子去噪相当于成像波场角度域衰减, 并且这种方法不需要抽取角道集.
同时, 从式(21)也可以看出, 在拉普拉斯算子去噪的同时也会损害成像的有用信息, 如分子中的频率项应该在成像前的数据上进行补偿.本文采用的是时间域积分方法对成像前数据进行补偿, 利用的关系表达式为[27]
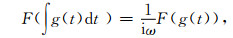
|
(24) |
其中, g(t)是时间域原始信号.
3 数值算例 3.1 均匀介质数值模拟为了进一步验证时空域有限差分相对传统有限差分有更好的数值模拟效果, 设计一个大小为201×201(网格数)、网格大小为10 m×10 m、速度为3000m/s的均匀介质模型.数值模拟时, 震源采用一个周期的正弦子波, 且其频率为50 Hz, 时间采样间隔为0.001s, 接收的记录长度为2s.震源位于(1000m, 1000m)处, 分别采用传统有限差分和时空域有限差分, 以时间上二阶精度、空间上二十阶精度进行数值模拟, 在数值模拟边界处理时, 采用完全匹配层(PML)吸收边界条件[36].
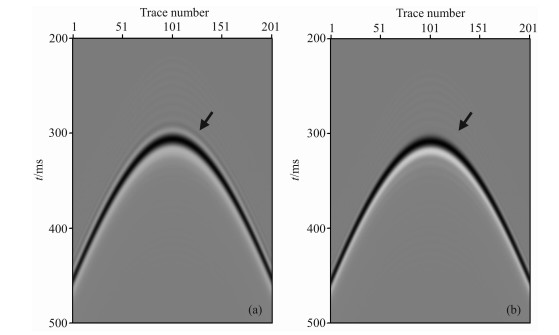
图 5(a, b)分别是采用传统有限差分和时空域有限差分模拟得到的0.3s时刻的波场快照.从快照波前面的形状来看, 传统有限差数值分模拟得到的波场快照的波形发生了畸变, 有较强频散, 而时空域有限差分模拟得到的波场快照的波形保持得比较好, 频散相对较弱.图 6(a, b)分别是采用传统有限差分和时空域有限差分模拟得到的单炮记录, 从(a)、(b)图对比也可以看出, 时空域有限差分模拟得到记录的频散更小, 波形保持得更好.因此介质模型中的数值模拟结果表明, 时空域有限差分数值模拟精度要高于传统有限差分的数值模拟精度[30].

|
图 5 在均勻介质中分别采用传统有限差分法(a)和时空域有限差分法(b)模拟得到的波场快照 Fig. 5 Snapshots computed by the cosvestiosal (a) and time-space (b) domain FD methods for the homogeneous acoustic model |
|
图 6 在均匀介质中分别采用传统有限差分法(a)和时空域有限差分法(b)模拟得到的单炮记录 Fig. 6 Shot records computed by the conventional (a) and time-space domain (b) FD methods for the homogeneous acoustic model |
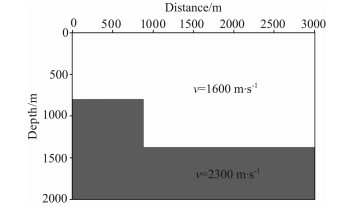
断层模型如图 7所示.模型大小为301×201(网格数), 网格大小为10m×10m, 断层上、下部分的速度分别为1600 m/s和2300 m/s.接收记录长度为3s, 时间步长为0.001s, 震源采用一个周期的25Hz的正弦子波, 一共58炮, 炮点位置在模型90m的深度面从距离最左边100 m处开始向右移动, 炮间距为50m, 每一炮都是全地表等距(10 m)接收.在数值模拟和逆时偏移中, 都以时间的二阶精度、空间的十二阶精度有限差分求解方程.图 8(a, b)是震源在(1500m, 90m)时分别采用传统有限差分和时空域有限差分模拟得到的1.5s时刻的波场快照.从图 8中对比传统有限差分和时空域有限差分数值模拟的结果表明, 时空域有限差分模拟得到的波场的频散更小, 精度更高.
|
图 7 断层速度模型 Fig. 7 The fault velocity model |
|
图 8 断层速度模型模拟得到的1.5s时刻的波场快照 (a)传统有限差分;(b)时空域有限差分. Fig. 8 Snapshots at 1.5 s for the fault model computed by the FD methods (a) The conventional FD method; (b) The time-space domain FD method. |
图 9和图 10分别是采用传统有限差分和时空域有限差分对断层速度模型进行逆时偏移而得到的剖面.对比去噪前后的偏移剖面, 可以看到, 高通滤波和拉普拉斯算子去噪都能有效地去除低频噪声, 但是高通滤波在去除噪声的同时, 也把断层的垂直部分滤掉了, 即对陡倾角信号有损害; 而拉普拉斯算子去噪能在去除噪声的同时保留好断层的垂直部分, 所以拉普拉斯算子去噪在逆时偏移的成像噪声消除中, 优于传统高通滤波方法.从图 9和图 10中也能看到, 逆时偏移使水平地层和垂直断层都能较好地成像, 且与模型相比, 界面成像位置准确, 尤其是时空域有限差分逆时偏移得到的最终剖面, 断层的垂直部分成像更清楚、更准确.

|
图 9 基于传统有限差分的断层速度模型逆时偏移剖面 (a)去噪前;(b)高通滤波去噪后;(c)拉普拉斯算子去噪后. Fig. 9 The RTM results of fautt model based os cosvestiosal FD method (a) Before denoising; (b) After high-pass filtering; (c) After Laplace filtering. |

|
图 10 基于时空域有限差分的断层速度模型逆时偏移剖面 (a)去噪前;(b)高通滤波去噪后;(c)拉普拉斯算子去噪后. Fig. 10 The RTM results of fautt model based os the time-space FD method (a) Before denoising; (b) After high-pass filtering; (c) After Laplace filtering. |
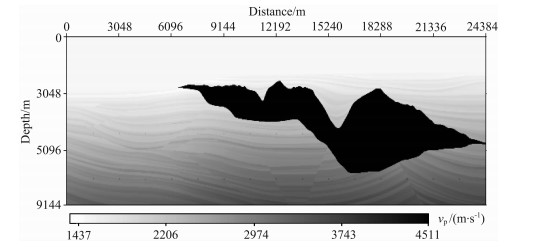
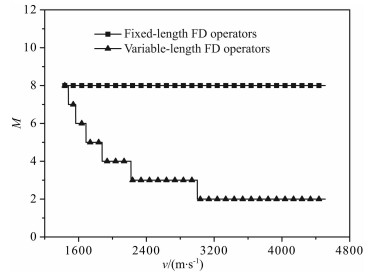
图 11是Sigsbee2A偏移速度模型.该模型的特点是拥有较为复杂的盐丘形状以及顶部构造, 因此经常被用来验证逆时偏移的效果以及比较噪声去除效果.模型大小为3201×1201(网格数), 网格大小为7.62m×7.62m, 速度范围为1437~4511m/s.接收记录的时间长度为12s, 时间步长为0.0005s, 震源采用一个周期的正弦子波, 其频率为30 Hz.一共200炮, 炮点位置是从距离模型最左边1524m处开始向右移动, 炮间距为106.68 m, 每一炮都是全地表等距(7.62m)接收, 震源和接收点位于同一深度面15.24m.将求解波动方程的误差控制在10-5内, 因此利用前面的计算公式(17), 在该模型的速度范围内, 如果空间导数采用固定的差分算子长度, 则算子长度取值应为8;如果采用自适应差分算子长度, 则算子长度如图 12所示, 范围为2~8.
|
图 11 Sigsbee 2A速度模型 Fig. 11 The Sigsbee 2A velocity model |
|
图 12 基于时空域有限差分方法的差分算子长度 Fig. 12 FD operator lengths for different velocities based on the time-space domain method |
数值模拟和逆时偏移的过程中, 基于时空域有限差分方法, 分别采用固定差分算子长度和自适应差分算子长度求解波动方程.将自适应差分算子长度应用到偏移的正向延拓和反向延拓计算时, 从理论上分析, 可以看到自适应差分算子长度平均上要短一些, 能有效改进偏移效率.我们在处理平台为ThinkPadR400笔记本电脑(Core2双核, 2.0GHz)上做了一个计算效率测试:统计5个炮点正向延拓的耗时, 如表 1所示, 从表中统计可以看出, 自适应差分算子长度有限差分的计算效率相对固定差分算子长度有限差分可以节约用时33%左右; 统计了5个炮点各自单炮逆时偏移成像整个过程的耗时, 如表 2所示, 从表中也可以看到, 在逆时偏移的过程中, 自适应差分算子长度有限差分策略能提高效率23%左右.图 13(a, b)是分别采用两类算子长度正演模拟得到的波场快照(4s时刻).从图 13可以看出, 采用两类算子长度正演模拟的结果基本一致.因此采用自适应有限差分法, 是一种在能保证精度要求的前提下, 提高计算效率的策略[31].
|
|
表 1 应用两类差分算子长度进行波场正向延拓的效率比较 Table 1 Comparison of computational deficiency of wave-field forward model by two kinds of FD operator lengths |
|
|
表 2 应用两类差分算子长度进行逆时偏移的效率比较 Table 2 Comparison of computational efficiency of RTM by two kinds of FD operator lengths |

|
图 13 对Sgsbee 2A模型模拟得到的炮点在4s时刻的波场快照 (a)固定差分算子长度为8; (b)自适应差分算子长度为2~8. Fig. 13 Wavefield snapshots at 4s for the Sigsbee 2A model (a) Fixed length FD operators are 8; (b) Variable FD operators range from 2 to 8. |
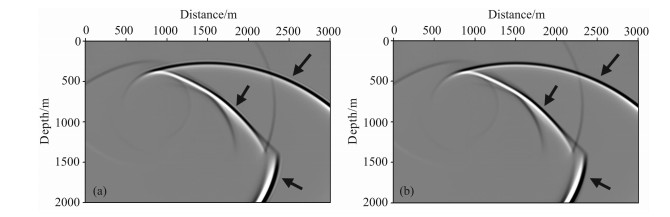
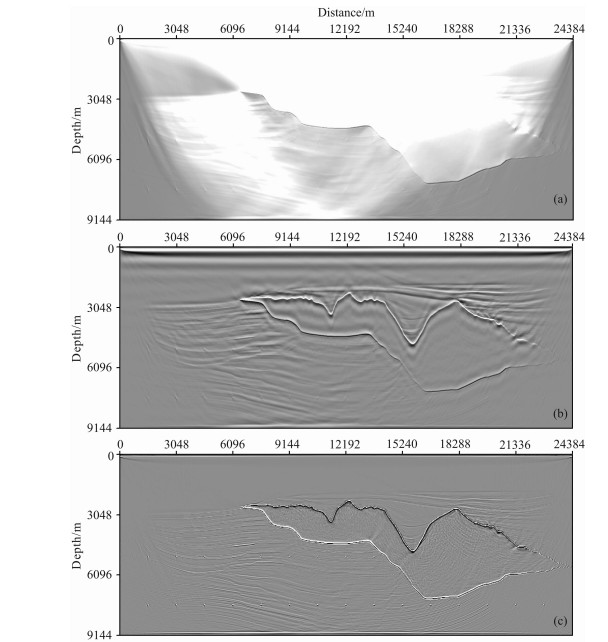
图 14a是Sigsbee2A速度模型采用时空域自适应有限差分方法逆时偏移的结果.虽然该速度模型对速度场做了平滑, 但在盐丘的边界处还是存在着强烈的速度间断, 会对逆时偏移带来较强烈的低频噪声, 可以看到很强的低频噪声集中在盐丘边界反射处, 如图 14a所示, 因此难以直接分析逆时偏移的效果.图 14b是采用高通滤波对逆时偏移结果进行去噪后的结果, 从该结果中可以看到, 经过高通滤波, 低频噪声得到了有效的压制, 逆时偏移的效果也显现出来了, 但还是没能很干净地去除噪声, 损害陡倾角信息.图 14c是应用拉普拉斯算子去噪后的逆时偏移剖面, 可以看到低频噪声得到了很好的消除, 与模型对比, 偏移成像结果比较好, 成像位置准确, 特别是在盐丘边界与盐丘底部成像清晰.由于受观测系统和地下的地质构造的影响, 可能会导致在岩丘底部有些区域照明度不够, 而要克服此问题, 则在偏移过程中需要进行照明度补偿[23, 37, 38].
|
图 14 Sigsbee 2A模型基于时空域自适应有限差分方法的逆时偏移剖面 (a)去噪前;(b)高通滤波后;(c)拉普拉斯算子去噪后. Fig. 14 The resutt of RTM for the Sigsbee 2A based os the time-space domain adaptive high-order FD method (a) Before denoising; (b) After high-pass filtering; (c) After Laplace filtering. |
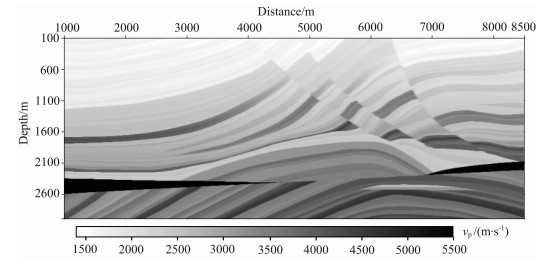
图 15是Marmousi速度模型, 对其进行重新采样后, 模型大小为921×300(网格数), 网格大小为10m×10m.该模型的速度范围1500.0~5500.0m/s, 总层数超过100层, 有大量的反射界面, 并含有一些陡倾角、逆冲断层、角度不整合面、地层隆起以及强烈的横向、纵向的速度变化.震源采用一个周期的正弦子波, 其频率为30 Hz, 一共240炮, 炮点位置在从距离最左边的2500 m处开始向右移动, 炮间距为20m, 右边放炮, 左边接收, 每一炮都是120道等距(20m)接收.接收记录长度为3s, 时间步长为0.001s.
|
图 15 Marmousi速度模型 Fig. 15 Marmousi velocity model |
将求解波动方程的误差控制在10-5内, 因此利用公式(17), 在该模型的速度范围内, 如果空间导数采用固定的差分算子长度, 算子长度M取值应为6, 如果采用自适应差分算子长度, 算子长度如图 16所示, 范围为2~6.
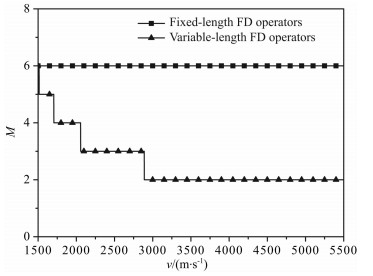
|
图 16 有限差分差分算子长度 Fig. 16 FD operator lengths for different velocities |
分别采用固定差分算子长度和自适应差分算子长度的时空域有限差分法求解波动方程和进行逆时偏移成像.表 3是统计两类差分算子长度进行逆时偏移的计算效率, 可以看到, 自适应差分算子长度有限差分逆时偏移能节时24%左右, 有效提高了计算效率.图 17a是基于时空域自适应高阶有限差分逆时偏移后的原始结果, 由于Marmousi模型存在大量的反射界面, 所以在逆时偏移之后, 其整个剖面上存在较强的低频噪声.图 17b是应用拉普拉斯算子去噪方法对图 17a进行处理后的成像剖面, 低频噪声得到了比较好的压制.从图 17b中也可看出, 逆时偏移对模型的主要构造都进行了较好的成像, 特别是在中浅部的大倾角构造、断裂及深部的角度不整合地层、目的层(地层隆起)均得到了比较好的成像.
|
|
表 3 应用两类差分算子长度进行逆时偏移的效率比较 Table 3 Comparison of computational deficiency of RTM by two kinds of FD operator lengths |
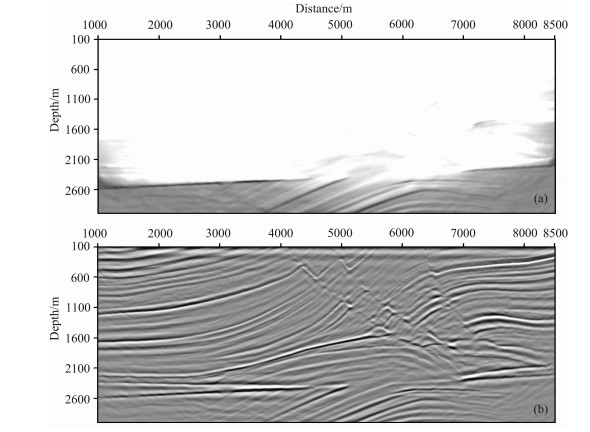
|
图 17 Marmousi模型基于时空域自适应有限差分方法的逆时偏移剖面 (a)去噪前;(b)去噪后. Fig. 17 The result of RTM for the Marmousi model based on the time-space domain adaptive high-order FD method (a) Before denoising, (b) After denoising. |
本文采用基于时空域有限差分的差分系数求解声波方程, 并分析了其数值频散和稳定性, 与传统有限差分进行了对比, 结果表明:时空域有限差分方法的模拟精度比传统的有限差分精度高、稳定性好, 数值模拟结果也表明时空域有限差分数值模拟的波形保持得更好、频散更小.在对不同的理论模型数据进行逆时偏移处理时, 将时空域的高阶有限差分法应用到实现声波叠前逆时偏移正向延拓和反向延拓的求解波动方程中, 可以提高求解方程的精度; 利用震源归一化互相关成像条件成像; 采用拉普拉斯算子去噪获得的成像更清晰、更准确.同时, 在声波叠前逆时偏移波场正向延拓与反向延拓的求解波动方程过程中, 采用自适应差分算子长度策略, 可以在保证数值模拟和逆时偏移精度的前提下, 有效地提高求解方程和成像的计算效率.
| [1] | Hemon C. Equations d'onde et modeles. Geophysical Prospecting , 1978, 26(4): 790-821. DOI:10.1111/gpr.1978.26.issue-4 |
| [2] | Baysal E, Kosloff D D, Sherwood J W C. Reverse time migration. Geophysics , 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [3] | McMechan G A. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting , 1983, 31(3): 413-420. DOI:10.1111/gpr.1983.31.issue-3 |
| [4] | Loewenthal D, Mufti I R. Reversed time migration in spatial frequency domain. Geophysics , 1983, 48(5): 627-635. DOI:10.1190/1.1441493 |
| [5] | Chang W F, McMechan G A. Reverse-time migration of offset vertical seismic profiling data using the excitation-time imaging condition. Geophysics , 1986, 51(1): 67-84. DOI:10.1190/1.1442041 |
| [6] | Chang W F, McMechan G A. Elastic reverse-time migration. Geophysics , 1987, 52(10): 1365-1375. DOI:10.1190/1.1442249 |
| [7] | Chang W F, McMechan G A. 3D acoustic prestack reverse-time migration. Geophysical Prospecting , 1990, 38(7): 737-756. DOI:10.1111/gpr.1990.38.issue-7 |
| [8] | Chang W F, McMechan G A. 3-D prestack migration in anisotropic media. Geophysics , 1993, 58(1): 79-90. DOI:10.1190/1.1443353 |
| [9] | Chang W F, McMechan G A. 3-D elastic prestack, reverse-time depth migration. Geophysics , 1994, 59(4): 597-609. DOI:10.1190/1.1443620 |
| [10] | Wu W, Lines L R, Lu H. Analysis of higher-order, finite-difference schemes in 3-D reverse time migration. Geophysics , 1996, 61(3): 845-856. DOI:10.1190/1.1444009 |
| [11] | Yoon K, Shin C, Suh S, et al. 3D reverse-time migration using the acoustic wave equation:An experience with the SEG/EAGE data set. The Leading Edge , 2003, 22(1): 38-41. DOI:10.1190/1.1542754 |
| [12] | Xu K, Zhou B, McMechan G A. Implementation of prestack reverse time migration using frequency-domain extrapolation. Geophysics , 2010, 75(2): 61-72. DOI:10.1190/1.3339386 |
| [13] | Duveneck E, Bakker P M. Stable P-wave modeling for reverse-time migration in tilted TI media. Geophysics , 2011, 76(2): S65-S75. DOI:10.1190/1.3533964 |
| [14] | Zhang Y, Zhang H Z, Zhang G Q. A stable TTI reverse time migration and its implementation. Geophysics , 2011, 76(3): WA3-WA11. DOI:10.1190/1.3554411 |
| [15] | da Silva Neto F, Costa J, Schleicher J, et al. 2.5D Reverse-time migration. Geophysics , 2011, 76(4): S143-S149. DOI:10.1190/1.3571272 |
| [16] | 底青云, 王妙月. 弹性波有限元逆时偏移技术研究. 地球物理学报 , 1997, 40(4): 570–579. Di Q Y, Wang M Y. The study of finite element reverse-time migration for elastic wave. Chinese J. Geophys. (in Chinese) , 1997, 40(4): 570-579. |
| [17] | 张会星, 宁书年. 弹性波动方程叠前逆时偏移. 中国矿业大学学报 , 2002, 31(5): 372–375. Zhang H X, Ning S N. Pre-stack reverse time migration of elastic wave equation. Journal of China University of Mining & Technology (in Chinese) , 2002, 31(5): 372-375. |
| [18] | 何兵寿, 张会星, 韩令贺, 等. 两种声波方程的叠前逆时深度偏移及比较. 石油地球物理勘探 , 2008, 43(6): 656–661, 684. He B S, Zhang H X, Han L H, et al. Pre-stack reverse-time depth migration of two acoustic wave equation and comparison between both. Oil Geophysical Prospecting (in Chinese) , 2008, 43(6): 656-661, 684. |
| [19] | 何兵寿, 张会星, 魏修成, 等. 双程声波方程叠前逆时深度偏移的成像条件. 石油地球物理勘探 , 2010, 45(2): 237–243. He B S, Zhang H X, Wei X C, et al. Imaging conditions for two-way acoustic wave equation pre-stack reverse-time depth migration. Oil Geophysical Prospecting (in Chinese) , 2010, 45(2): 237-243. |
| [20] | 杜启振, 秦童. 横向各向同性介质弹性波多分量叠前逆时偏移. 地球物理学报 , 2009, 52(3): 801–807. Du Q Z, Qin T. Multicomponent pre-stack reverse-time migration of elastic waves in transverse isotropic medium. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 801-807. |
| [21] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [22] | 王童奎, 付兴深, 朱德献, 等. 谱元法叠前逆时偏移研究. 地球物理学进展 , 2008, 23(3): 681–685. Wang T K, Fu X S, Zhu D X, et al. Spectral-element method for prestack reverse-time migration. Progress in Geophysics (in Chinese) , 2008, 23(3): 681-685. |
| [23] | Liu Y K, Chang X, Jin D G, et al. Reverse time migration of multiples for subsalt imaging. Geophysics , 2011, 76(5): WB209-WB216. DOI:10.1190/geo2010-0312.1 |
| [24] | Chattopadhyay S, McMechan G A. Imaging conditions for prestack reverse-time migration. Geophysics , 2008, 73(3): S81-S89. DOI:10.1190/1.2903822 |
| [25] | 李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报 , 2010, 53(12): 2938–2943. Li B, Liu H W, Liu G F, et al. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 2938-2943. |
| [26] | Zhang Y, Sun J. Practical issues in reverse time migration:true amplitude gathers, noise removal and harmonic-source encoding. First Break , 2009, 26(1): 19-25. |
| [27] | 刘红伟, 刘洪, 邹振, 等. 地震叠前逆时偏移中的去噪与存储. 地球物理学报 , 2010, 53(9): 2171–2180. Liu H W, Liu H, Zou Z, et al. The problems of denoise and storage in seismic reverse time migration. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2171-2180. |
| [28] | Karazincir M H, Gerrard C M. Explicit high-order reverse time pre-stack depth migration. 76th Annual International Meeting, SEG, Expanded Abstracts, 2006:2353-2367. |
| [29] | 刘洋, 李承楚, 牟永光. 任意偶数阶精度有限差分法数值模拟. 石油地球物理勘探 , 1998, 33(1): 1–10. Liu Y, Li C C, Mou Y G. Finite-difference numerical modeling of any even-order accuracy. Oil Geophysical Prospecting (in Chinese) , 1998, 33(1): 1-10. |
| [30] | Liu Y, Sen M K. A new time-space domain high-order finite-difference method for the acoustic wave equation. Journal of Computational Physics , 2009, 228(23): 8779-8806. DOI:10.1016/j.jcp.2009.08.027 |
| [31] | Liu Y, Sen M K. Finite-difference modeling with adaptive variable-length spatial operators. Geophysics , 2011, 76(4): T79-T89. DOI:10.1190/1.3587223 |
| [32] | Chen J B. High-order time discretizations in seismic modeling. Geophysics , 2007, 72(5): SM115-SM122. DOI:10.1190/1.2750424 |
| [33] | Claerbout J F. Toward a unified theory of reflector mapping. Geophysics , 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [34] | Kindelan M, Kamel A, Sguazzero P. On the construction and efficiency of staggered numerical differentiators for the wave equation. Geophysics , 1990, 55(1): 107-110. DOI:10.1190/1.1442763 |
| [35] | Lecomte I. Resolution and illumination analyses in PSDM:A ray-based approach. The Leading Edge , 2008, 27(5): 650-663. DOI:10.1190/1.2919584 |
| [36] | Bérenger J P. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics , 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [37] | 陈生昌, 马在田, WuR S. 波动方程偏移成像阴影的照明补偿. 地球物理学报 , 2007, 50(3): 844–850. Chen S C, Ma Z T, Wu R S. Illumination compensation for wave equation migration shadow. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 844-850. |
| [38] | 陈生昌, 王汉闯. 基于平面波照明的偏移成像补偿. 地球物理学报 , 2010, 53(7): 1710–1715. Chen S C, Wang H C. Migration compensation with plane wave illumination. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1710-1715. |
 2013, Vol. 56
2013, Vol. 56


