地球扁率在地质历史上的变化下限

引用本文

王君恒, 李新均, 张煜颖等. 地球扁率在地质历史上的变化下限. 地球物理学报, 2013, 56(3): 842-847, doi: 10.6038/cjg20130313. 复制到剪切板

Wang J H, Li X J, Zhang Y Y, et al. The lower limit of variation of the Earth's oblateness in geological epoch. Chinese J. Geophys. (in Chinese), 2013, 56(3): 842-847, doi: 10.6038/cjg20130313. 复制到剪切板

地球扁率在地质历史上的变化下限

王君恒^1,2 , 李新均^1,2 , 张煜颖^1,2 , 王晓滨^1,2 , 王静远³

1. 地下信息探测技术与仪器教育部重点实验室, 北京 100083;
2. 中国地质大学(北京)地球物理与信息技术学院, 北京 100083;
3. 密西根大学安娜堡, 美国 48109

收稿日期 2012-04-06, 2012-06-28 收修定稿

作者简介: 王君恒, 男, 1962年生, 山东青岛人, 博士, 中国地质大学(北京)地球物理与信息技术学院副教授, 主要从事应用地球物理和理论地球物理研究工作.E-mail:W1128@cugb.edu.cn

摘要: 为研究地球形状的长期变化, 将地球假设为弹性椭球体, 根据弹性动力学理论导出地球的扁率下限公式, 扁率与地球的平均密度ρ、引力加速度g、自转角速度ω、平均半径R、弹性模量E、泊松比v相关.将新星云假说下地质历史时期半径、质量和角速度变化值代入公式计算出各地质历史时期地球扁率值, 作为地球扁率变化值的下限值.地球的扁率自地球形成以来总体变化趋势是在减小.

关键词: 地球扁率下限平均密度引力加速度自转角速度平均半径

The lower limit of variation of the Earth's oblateness in geological epoch

WANG Jun-Heng^1,2, LI Xin-Jun^1,2, ZHANG Yu-Ying^1,2, WANG Xiao-Bin^1,2, WANG Jing-Yuan³

1. Key Laboratory of Geo-detection, Ministry of Education, Beijing 100083, China;
2. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China;
3. University of Michigan Ann Arbor 48109, USA

Abstract: A variation in the earth's shape is one of the basic problems of earth evolution. A variation in the earth's oblateness can be used to understand the variation of the earth's shape.Assuming the Earth is flexible ellipsoid, according to the theory of elastic dynamics, we derived the formula for minimum oblateness of the Earth and conclude that oblateness of the Earth is a function of the average density of the Earth ρ, the gravitational acceleration g, rotation rate ω, average radius R, elastic modulus E and Poisson's ratio v. Apply parameters such as the radius, mass, and the change in angular velocity of the Earth, which are based on the new nebular hypothesis, into the formula to calculate the lower limit of oblateness of the Earth in different geological epoch. The oblateness of the Earth has signs of reduction in its magnitude since the formation of the Earth..

Key words: Earth's oblateness lower limit Gravitational acceleration Rotation angular velocity Average density Average radius

1 引言

现代地球的几何形状是椭球体, 为固液混合体, 因此不易设计准确物理模型, 从而准确地研究扁率在地质历史上的真实变化值.作者以往的工作中给出了地球扁率在其历史上变化的上限值^[1], 并对地球扁率研究历史及现状做了详细综述.本文拟从弹性力学理论出发, 将地球作为完全弹性体, 推导出椭圆极向周长与平均半径、平均密度、质量、角速度、弹性模量和泊松比之间的第二类椭圆积分关系式, 进而导出地球扁率公式, 将新星云假说下地球各个地质历史时期的形态参量代人公式计算后得出扁率变化值, 作为地球扁率变化的下限值.

2 地球均匀各项同性弹性力学模型

椭球形状的地球从地表到地心粗略地分为A到G共7个圈层, 其中E层为液态, B、C、D层主要为固体, 部分为液体.将地球作为整体来研究时, 不同研究目的和方法所涉及的整体模型不同, 如早期重力研究时将地球等效为"牛顿"球; 研究地球扁率46亿年以来长期变化时不能设计出准确模型, 近似地将地球看作具有引力和自转离心力的弹性球体, 均匀各向同性, 由于弹性模型比地球实际的粘弹性混合体变形要小, 模型所获得的扁率要小于地球实际扁率, 所以均匀各项同性弹性模型扁率变化结果应作为实际地球扁率变化的下限.

球体均匀各项同性弹性模型为球形地球在引力和自转离心力的作用下产生形变, 成为椭球体, 取球坐标系, 其位移u满足(Navier)方程^[2-3]

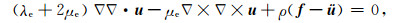
(1)

其中λe和μe.分别是Lame常数, 在球坐标系中

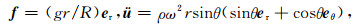
(2)

R和ρ分别为地球平均半径和平均密度, g=GM/R²为球表面的引力加速度, M为地球质量, G为引力常数, ω为自转角速度.(1)式满足边界条件: u在r=0处有限、r=R时r方向主应力t_rr=0的解^[4]

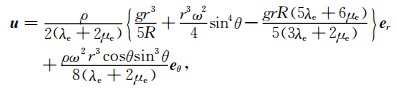
(3)

其中er, eθ为单位矢量, 根据(3)推导无限小拉格郎日应变张量E(e_ij)^[5]

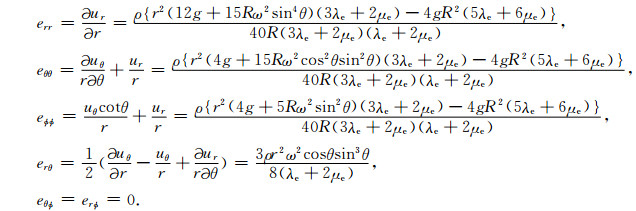
(4)

(4)式中, 当r=R时, 为地球表面上拉格郎日应变张量, 根据拉格郎日应变张量E(E_ij=e_ij)和格林应变张量C(C_ij)的下列关系

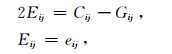
(5)

得到地球表面无限小格林应变张量C_ij这里G_ij是拉格郎日坐标系的度规张量, 即球坐标的度规张量.有

则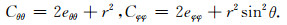

那么, 要研究变形地球的表面上无限小格林应变张量为

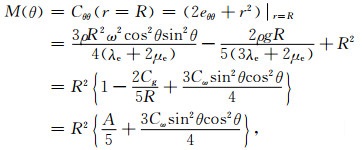
(6)

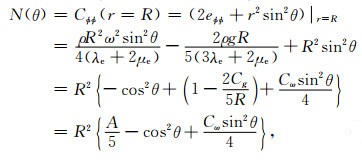
(7)

其中C_g和C_ω是反映地球的引力和自转的常数, 有

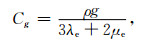
(8a)

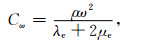
(8b)

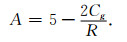
(9)

要求出变形地球的扁率值, 需求出极向和经向周长.经过繁琐推导, 极向圆周形状为椭圆, 周长为

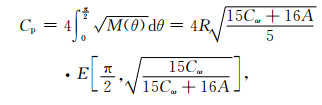
(10)

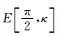
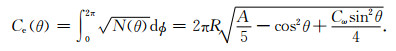
(10)式中表示第二类完全椭圆积分^[6], 为定值, 可以通过代人函数或查表获取.不同纬度的经向周长为

(11)

以下分别对只有引力和只有自转两种状况进行讨论.

2.1 当C_g≠0, C_ω=0, 即只有引力的状况

在(10)和(11)式中令C_ω=0且在(11)式中取θ=π/2, 可得地球极向周长和赤道周长

R'是地球经引力形变后的半径.显然, 弹性地球变形后仍是球体, 只是半径减小, 由于R'不能为虚数, 所以有A≥0, 再根据(8a)和(9)式有

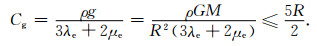
(14)

对于不自转, 只有引力作用且密度均匀的球体, 质量上限应为

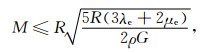
(15)

(15)式类似广义相对论给出的密度均匀星球质量上限.通过上述分析可知, 在地球弹性模型中, 可以认为引力是等平衡的, 引力作用没有改变地球的形状.

由于(3)式为(1)式的近似解, 根据R'=R + u_r|r=R来求变形之后的半径不妥.

2.2 当C_g=0, C_ω≠0, 即只有自转的状况

令C_g=0, 得A=5, 则可将仅有自转时地球表面不同纬度的经向周长和极向周长分别表示为

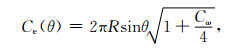
(16)

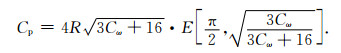
(17)

从(16)、(17)式可以看出, 自转使球形地球形状发生改变, 变为椭球, 同时自转使经向周长增大.赤道半径变为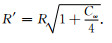

当C_g≠0, C_ω≠0, 在既有引力又自转的情况, 这时赤道周长为

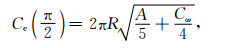
(18)

由于赤道为圆形, 赤道半径为

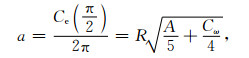
(19)

极向周长为

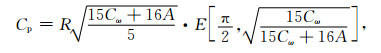
(20)

极向圆周形状为椭圆, 根据椭圆周长标准公式

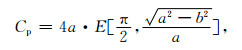
(21)

假设极向椭圆长、短轴分别为a和b对比(20)和(21)式得

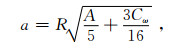
(22)

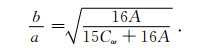
(23)

将(19)和(22)式对比, 发现有微小差异, 差异来自于(20)中C_p为模型线弹性解, 忽略了形变u对坐标导数的二次项, 而(21)中椭圆的周长为精确解.

根据(23)式地球扁率下限公式为

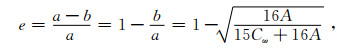
(24)

(24)式为计算地球扁率变化下限的最终公式, 只要确定各个地质历史时期的A和C_ω, 就可以研究扁率变化的下限.

4 各参数值的确定

在(8)和(9)式中有两个常量λe、μe和四个变量ρ、g、ω、R.考虑较为简单情况, 计算时λe、μe常数需用弹性模量(杨氏)E和泊松比v替换

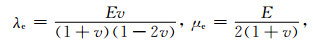
(25)

则有

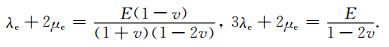
(26)

当地球为完全塑性模型时, 扁率上限和目前的地球扁率非常接近^[1], 所以弹性地球参数总体应接近塑性, 根据试算, 取地球的弹性模量E应为接近塑性模型参数的一个值如0.0006 Pa, 地球泊松比v的正常范围0.27~0.5(固体-液体), 取接近0.5的一个值如0.45.需要指出的是下限曲线对弹性模量E和泊松比v比较敏感, 这与弹性模量E和泊松比v的物理意义相一致, 当E=0或v接近0.5时, 介质为液体.可取多个弹性模量和泊松比分别做出下限曲线, 以作对比.

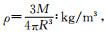
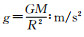
四个变量ρ、g、ω、R可以归结为三个, 即M、ω、R; 考证地质历史时期这三个量的变化, 就可以算出相应的扁率变化下限.所有物理量取国际标准单位, 计算平均密度和引力加速度时近似把地球当作正球体, 各参数单位分别为:地球质量M :kg, 地球半径R :m, 自转角速度ω :rad/s, 弹性模量E: Pa, 地球密度引力加速度, 万有引力常量G=6.67×10^-11 (N·m²/kg²), 泊松比v无量纲.

5 计算实例(新星云假说)

以新星云假说为例计算扁率变化下限值^[7-9].在涉及年代时, 文中叙述所使用的年限有两个起点, 一个是以现在为0时点的地质时标, 例如35亿年前, 指的是以往距今35亿年.另一个是以地球46亿年前诞生为0时点的一般时标, 例如地球诞生后5亿年, 是指41亿年前.地质历史时期(epoch)采用2亿年取值间隔, 个别间隔1亿年.

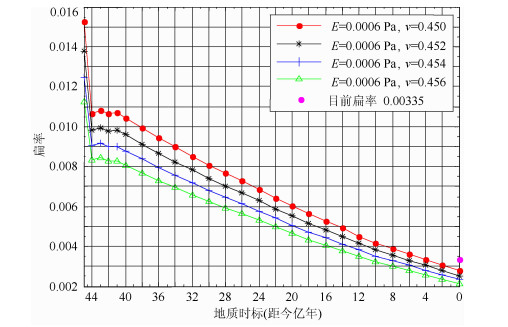
新星云假说关于M、ω、R的数据如表 1, 计算结果如表 2, 扁率变化下限曲线见图 1和图 2.

图 1 不同泊松比对应地球扁率下限变化曲线 Fig. 1 The lower limit variation curves of the flexible Earth model'oblatenesswith different Poisson's ratio v

图 2 不同弹性模量对应地球扁率下限变化曲线 Fig. 2 The lower limit variation curves of the flexible Earth model's oblateness with different elastic modulus E

表 1 新星云假说地球参数表^[1] Table 1 Shape parameters of the Earth in geological epoch

时间 (地质时标）	平均半径 (×10³km)	质量 (×10²⁴ kg)	自转角速度 (×10^-3rad/s)
46	5.7347	5.3784	0.1527
45	6.1624	5.774	0.151
44	6.4106	5.956	0.1492
43	6.3902	5.965	0.1475
42	6.3843	5.9651	0.1457
41	6.3719	5.9754	0.144
40	6.3719	5.9754	0.1423
38	6.3719	5.9754	0.1388
36	6.3719	5.9755	0.1353
34	6.3719	5.9755	0.1319
32	6.3719	5.9755	0.1284
30	6.3719	5.9756	0.1249
28	6.3692	5.9756	0.1215
26	6.3654	5.9756	0.118
24	6.3653	5.9757	0.1145
22	6.3697	5.9757	0.1111
20	6.3719	5.9757	0.1076
18	6.3719	5.9757	0.1041
16	6.3719	5.9758	0.1007
14	6.3719	5.9758	0.0972
12	6.3782	5.9758	0.0937
10	6.3808	5.9759	0.0902
8	6.3784	5.9759	0.0868
6	6.3719	5.9759	0.0833
4	6.3719	5.9759	0.0798
2	6.3719	5.976	0.0764
0	6.3719	5.976	0.0729
目前实测值	6.3719	5.976	0.0729

表 1 新星云假说地球参数表^[1] Table 1 Shape parameters of the Earth in geological epoch

表 2 星云假说地球地质历史计算参数表 Table 2 The shape parameters of the Earth in geological epoch by calculation(The table 2 is compiled by the authors)

地质时标	平均半径 R（×10³km)	质量 M(×10²⁴ kg)	自转角速度 w（×10-³rad/s)	平均密度 ρ(kg/m²)	引力加速度 g(m/s²)	地球扁率 E=0. 0006. v=0. 45
46	5.7347	5.3784	0.1527	6808.2	10.908	0.04467
45	6.1624	5.7740	0.1510	5890.3	10.142	0.01528
44	6.4106	5. 9560	0.1492	5397.2	9.6668	0.01065
43	6.3902	5.9650	0.1475	5457.3	9.7433	0.01081
42	6.3843	5.9651	0.1457	5472.5	9.7615	0.01065
41	6.3719	5.9754	0.1440	5514.1	9.8165	0.01069
40	6.3719	5.9754	0.1423	5514.1	9.8165	0.01044
38	6.3719	5.9754	0.1388	5514.1	9.8165	0.00994
36	6.3719	5.9755	0.1353	5514.2	9.8166	0.00945
34	6.3719	5.9755	0.1319	5514.2	9.8166	0.00899
32	6.3719	5.9755	0.1284	5514.2	9.8166	0.00853
30	6.3719	5.9756	0.1249	5514.2	9.8168	0.00807
28	6.3692	5.9756	0.1215	5521.3	9.8251	0.00768
26	6.3654	5.9756	0.1180	5531.2	9.8368	0.00730
24	6.3653	5.9757	0.1145	5531.5	9.8373	0.00687
22	6.3697	5.9757	0.1111	5520.1	9.8237	0.00643
20	6.3719	5.9757	0.1076	5514.3	9.8170	0.00601
18	6.3719	5.9757	0.1041	5514.3	9.8170	0.00563
16	6.3719	5.9758	0.1007	5514.4	9.8171	0.00527
14	6.3719	5.9758	0.0972	5514.4	9.8171	0.00491
12	6.3782	5.9758	0.0937	5498.1	9.7977	0.00452
10	6.3808	5.9759	0.0902	5491.5	9.7899	0.00417
8	6.3784	5.9759	0.0868	5497.7	9.7973	0.00388
6	6.3719	5.9759	0.0833	5514.5	9.8173	0.00362
4	6.3719	5.9759	0.0798	5514.5	9.8173	0.00332
2	6.3719	5.9760	0.0764	5514.6	9.8174	0.00305
0	6.3719	5.9760	0.0729	5514.6	9.8174	0.00277
目前值	6.3719	5.976	0.0729	5514.6	9.8174	0.00335

表 2 星云假说地球地质历史计算参数表 Table 2 The shape parameters of the Earth in geological epoch by calculation(The table 2 is compiled by the authors)

在44亿年前(见图 1), 地球形成过程中扁率急剧减小; 44-41亿年, 扁率有增有减, 说明地球形成初期经历较为复杂的过程.自41亿年至今地球扁率逐渐变小, 其下限由0.01069变为0.00227, 减少了78%.图 1中不同颜色的曲线表示相同弹性模量E, 不同泊松比v所对应的下限曲线.随泊松比v增大, 下限曲线向下移动, 远离真值.关于泊松比v对扁率的总体影响较为复杂, 另文探讨.

图 2中不同颜色的曲线表示相同泊松比v, 不同弹性模量E所对应的下限曲线.随弹性模量E增大, 下限曲线向下移动, 远离真值.

地球总体的弹性模量E=0.0006 Pa, 与各个圈层岩石的弹性模量相差巨大, 如花岗岩弹性模量为0.15~0.4×10¹¹ Pa, 可见地球由高弹性模量的材料组合后, 总体弹性模量却很小, 因此可以做出如此推断, 这些岩石块体是松散组合的并且相互的缝隙之间还有液体和气体做润滑, 表现出总体弹性模量较小.而地球整体泊松比v的取值接近液体也说明地球整体形变比完全刚性要充分得多, 地球总体形变特征更象液体球, 接近静力学平衡.

6 结论

地球弹性模型公式(24)较好的刻画了密度均匀弹性固体地球的扁率下限.

地球扁率下限主要影响因素为平均半径、质量、自转角速度.自转角速度是主要因素, 弹性模量E泊松比v不影响曲线形态.

地球作为固液混合椭球体的整体刚性远远小于由连续的钢铁或连续的岩浆岩组成的球体的刚性, 地球整体更接近塑性体, 接近静力学平衡态.

文中仅给出新星云假说数据, 不同的假说下, 数据可能有差异.

如果弹性模量E泊松比v取得合适, 修改模型可以尝试模拟地球扁率变化真实值.

R的取值范围有改进的可能.

致谢

感谢曾华霖教授对论文提出宝贵意见, 感谢与姚长利教授的有意义的探讨.感谢刘光鼎院士的培养指导和关心.

参考文献

[1]	王君恒, 郭雷, 王健楠, 等. 地球扁率在其历史上的变化. 地球物理学进展 , 2010, 25(1): 143–150. Wang J H, Guo L, Wang J N, et al. The change of earth oblateness in its history. Progress in Geophys. (in Chinese) , 2010, 25(1): 143-150.

[2]	Eringen A C. Mechanics of Continua, Second Edition. Robert R Krieger Publishing Company , 1980: 206.

[3]	Landau L D, Lifshitz E M. Mechanics of Continuous Media. New York: Pergamon Press, 1982 .

[4]	强稳朝. 自引力旋转球的整体变形几何. 物理学报 , 2001, 9(9): 1643–1647. Qiang W.C. Global Deformation Geometry of A Self-Gravitational Rotational Ball. Acta Physica Sinica (in Chinese) , 2001, 9(9): 1643-1647.

[5]	程祖依. 弹性动力学基础. 北京: 中国地质大学出版社, 1989 : 159 . Cheng Z.Y. The Based of Elastodynamics (in Chinese). Beijing: China University of Geosciences Press, 1989 : 159 .

[6]	Gradshteyn I S, Ryzhik I M. Table of Integrals Series and Products. New York: Academic Press, 2000 : 7 .

[7]	戴文赛. 太阳系演化学(上册). 上海: 上海科学技术出版社, 1979 . Dai W S. The Evolution of Solar System (in Chinese). Shanghai: Science and Technology Press, 1979 .

[8]	戴文赛, 胡中为. 论太阳系的起源. 中国科学 , 1980(3): 254–280. Dai W S, Hu Z W. The Origin of Solar System. Science of China (in Chinese) , 1980(3): 254-280.

[9]	戴文赛, 陈道汉. 太阳系起源各种学说的评价. 天文学报 , 1976, 1(17): 93–105. Dai W S, Chen D H. Critical Review of Theories on the Origin of the Solar System. Acta Astronomica Sinica (in Chinese) , 1976, 1(17): 93-105.


地球物理学报 2013, Vol. 56 Issue (3): 842-847	PDF