2. 中国地震局地震研究所(地震大地测量重点实验室), 武汉 430071;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Earthquake Geodesy, Institute of Seismology, CEA, Wuhan 430071, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
全球海平面变化对温度变化和地球表面大气、陆地水、海洋等各圈层之间的冰水质量交换非常敏感,可用来作为全球气候变化的指示器,是全球气候变化研究中的关键要素之一.通过验潮站观测[1]、海洋浮标观测[2]和理论数值模拟[3]等多种传统观测及理论模拟途径,可获取在月或更长时间尺度上的海平面变化.随着空间大地测量技术的飞速发展,测高卫星和重力卫星以其快速、高效和几近全球覆盖特性,实现了高精度和高时空分辨率全球海平面时变特征提取.其中测高卫星刻画了总体海面高变化,重力卫星只对质量迁移引起的海面高变化敏感,而与温盐热膨胀导致的海面高变化无关.最近研究结果表明,重力场恢复与气候试验卫星GRACE(Gravity Recovery AndClimateExperiment)观测得到的海面高变化要比传统的海洋模式输出结果大得多[4].经分析,除GRACE自身的误差影响外,模式的内在不足可能是最主要的原因.其内在不足表现为:1)由于对如海岸线的几何细节特征、洋底地形和沿海区域的风场效应等确定海平面变化的重要参数难以准确刻画,低分辨率的全球海洋模式很难较好地模拟近海区域的海平面变化;2)在海洋模式模拟的过程中一般遵循体积守恒而非质量守恒,忽略了河流径流驱动等质量交换因素的影响.同时,1993-2002年近10年的验潮站区域面积加权平均得到的海平面上升趋势速率4.0 mm/a,比测高卫星TOPEX/ Poseidon得到的全球平均值2.8 mm/a较大[5],这暗示了近海海洋特征和远海有着较大程度上的不同.
目前大多数海洋模式采用Boussmesq近似,服从整体海洋体积守恒而非质量守恒.为克服这一不足,一般在海洋模式输出结果的基础上添加均一厚度的水层来保持整体海洋质量守恒.但这种人为方法忽略了全球质量重新分布引起的重力位变化和由此带来的质量负荷自吸引效应SAL(Sel--attraction andLoading)对海平面时空变化的影响.质量负荷的迁移,尤其是陆地水质量的迁移,会对海平面变化的空间分布形式产生很大的影响[6].Woodward[7]计算结果表明,在刚性地球假设下,由于自吸引效应的影响,冰雪质量的融化可以导致非均一的海平面变化.事实上,在刚性假设下,单位点负荷对海平面的影响约在离该点负荷20°区间范围[8].这可能解释模型结果与实测观测结果符合得比较差和近海与远海海平面变化差异的原因.最近,Tamsea[9]基于大气、海洋和陆地水数值模式结果分析了1980-1997年SAL效应对海平面的周年变化的影响,发现SAL可以导致约1.5~18 mm海平面周年振幅变化.但由于传统观测手段的局限,现有水文模型缺少一些必要的水文循环一阶组成部分,如地下水储量、敞流湖泊和极地冰盖等,且在永久积雪如山岳冰川区域数值精度较差.模式的这些内在缺陷会使得依据模式结果计算得到的受迫海平面变化SAL结果含有较大的偏差.诸多研究结果表明,GRACE所观测的时变重力场变化能准确地反演区域水储量变化,尤其是在具有显著变化的极地冰盖和山岳冰川区域[10-13].这可以很大程度上弥补水文模型在这些区域数值精度较差的不足,可以更好地定量分析SAL这种地球物理机制对海平面变化的影响.基于这个思想,本文在海平面方程基础上,考虑自吸引效应和旋转离心力位的影响,分析了陆地水储量变化、大气质量变化和非潮汐海洋质量变化在2003-2010年对海平面周年变化的影响,并尝试在海洋模式得到的洋底压力结果中引人SAL,以期能更好地解释验潮站观测结果.
2 计算方法海平面高定义为瞬时海水面与大地水准面之间的距离,不同时刻的海平面高变化即为海平面高度差变化.Clark & Farrell[14]给出了考虑引力自吸引下的冰后回弹(GIA, Glacial Isotatic Adjustment)作用引起的海平面变化的理论框架,迄今为止它仍是研究GIA过程的标准理论框架.初始的解法是时空卷积,海洋和冰体被离散化为圆盘型负荷[14].Milne[15]首次给出了融合直接效应和旋转扰动位自洽性海平面方程理论框架.Kendall[16]在此基础上考虑了海平面形状以及着地冰前进或退缩的影响,并给出了具体的算法.GIA考虑的时间尺度一般为1~10千年,需要考虑地球内部黏弹性的影响.在更短的时间尺度上,如本文考虑的周年时间尺度,只考虑地球弹性项而忽略黏弹性的影响,忽略海平面变化和着地冰范围变化,即在Kendall文中的函数C,β都为常函数,所得的结果精度已经足够,这在很大程度上简化了海平面方程.
2.1 非地球自转效应的海平面方程根据定义,影响海平面变化的主要因素包含三个方面:1)瞬时水准面位的变化;2)质量负荷导致的固体地球垂直形变;3)系统各圈层之间的水质量交换.根据Farrell[14]负荷理论,海平面方程格林函数表达式:

|
(1) |
其中(θ,φ)和(θ',φ')对应表示待求点和负荷点的余纬和东经,α为两点之间的球面角距cosα=cosθcosθ'+sinθsinθ'cos(φ'-φ),g为表面重力加速度,R为地球平均半径,Ω是球面单位角dΩ=sinθdθdφ, 由于海洋和陆地不规则分布,两者之间的质量交换产生的瞬时等势海平面与初始大地水准面之间存在位差,引人空间常数项Δφ/g保证全球质量守恒[17].C是海洋盆地函数,在陆地和海洋上的值分别为1和0.格林函数Gφ展开为勒让德函数形式:

|
(2) |
这里Me是地球整体质量,Pm是m阶勒让德函数,h'm,k'm为m阶负荷勒夫数,分别表征固体地球垂向位移和地球形变(质量重新分布)导致的附加位影响.整体负荷L按空间分为陆地I(θ,φ)和海洋SL(θ,φ)变化,即

|
(3) |
ρw是水密度1000 kg/m3.将(3)式作球谐展开,基于面谐函数正交性和球谐加法定理,联合(1)-(2)式,在球谐域海平面方程可以描述为:
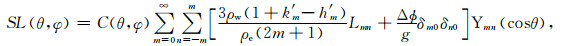
|
(4) |
其中δ为克罗朗内克符号,Ymn是m阶n次面球谐系数,ρe是地球平均密度5517/m3.
表面负荷变化同时也会引起地球旋转矢量的变化,进一步造成离心力位的变化,从而反过来影响海平面的变化[18].Milne[19]给出了负荷与离心力位变化的位系数展开关系式.由于本文考虑的为短时间尺度效应,为计算方便,下面对Milne导出的结果进行了简化.
2.2 地球自转反馈影响定义右手笛卡儿坐标系,坐标原点位于地球质心,x1轴指向格林威治方向,x2指向x1的东90°方向. Γ为地球的初始角速度,mi(i=1,2,3)为由于负荷作用引起的xi轴旋转角速度扰动变化.参照Milne公式(A8),极移运动的微小扰动对离心力位场的影响在谱域展开为:
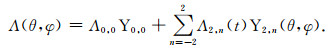
|
(5) |
由于假定地球自转变化激发扰动旋转角速度是微小量,假定它们之间的互积等二阶小量可以忽略,可对Milne(33a)-(33d)公式简写:
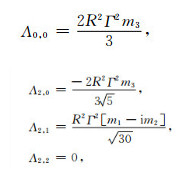
|
(6) |
Λ2, -m=(-1)mΛ2, m*,表示复数的共轭,i为-1的虚方根.只考虑弹性地球影响,忽略黏弹性作用,极移分量m1和m2与质量负荷球谐展开系数之间的关系式为:

|
(7) |
Γ0为黏弹地球的摆动频率,A与C分别为初始地球的主赤道惯性矩和轴向惯性矩,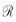
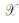
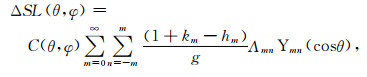
|
(8) |
km,hm表示m阶勒夫数.值得注意的是旋转位势场主要由零阶和二阶项球谐系数描述[18].分析式(6)-(7)可以看到m3远小于m1,m2,同时m1,m2由二阶1次项系数决定,因此在海平面方程中引入地球自转反馈效应在海洋上的影响服从P21间分布.
综合(4)式与(8)式,可以得到在球对称的完全弹性地球条件下,假设海洋盆地函数为常函数,考虑地球自转回馈效应的海平面与负荷球谐函数之间相关表达形式:
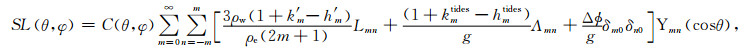
|
(9) |
方程(9)左右两边都包含待定求解参数SL (右边Lmn包含SLmn参数),因此需要迭代求解.迭代初始值为(9)式中的零阶项,对应于为维持大气、海洋和陆地水整体质量平衡的海平面变化引人的改正项.判定迭代收敛条件(公式(0))为两次迭代SL结果的球谐累加谱差别百分比小于10-6,i为迭代次数,实际计算中一般8次左右即可收敛.
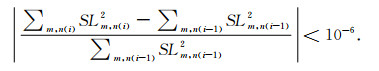
|
(10) |
由(9)式可知,当讨论海平面的周年变化时,需要考虑尽量多的负荷质量贡献因子.这里与Clarke[6]和Tamisiea[9]策略类似,主要讨论三种质量迁移的SAL效应对海平面变化的影响:1)全球陆地水储量变化; 2)非潮汐海水质量变化; 3)大气水含量变化.
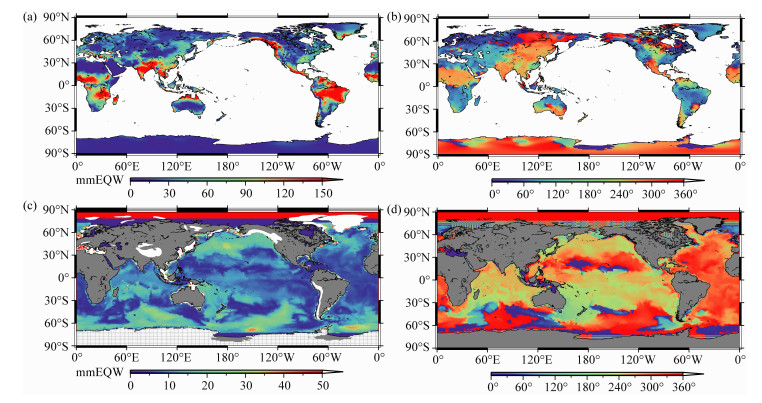
3.1 陆地水储量变化目前陆地水储量时变信息可由多种数值模型获取.这里我们采用美国国家海洋大气局气象预报中心CPC(ClimatePrediction Center)提供的全球陆地同化水文模式[20].该模式采用的输人数据包括CPC观测的降水分析结果以及太阳辐射、地表气压、气温和NCEP(National Centers of Environmental Prediction)提供的地表水平风速数据.输出结果包括植被含水、直到2 m深度的土壤湿度等数据.空间分辨率为0.5°,时间分辨率为1月.陆地水储量包括土壤水、地下水(0~2 m)、雪水和植被水的总和.由于降雪数据在南极冰盖、格陵兰岛冰盖、阿拉斯加冰川、智利冰川等极地或陆地冰川(盖)区域存在较大误差(空间分布如图 1c中白色区域所示),因此对这些区域的数据由美国空间中心CSRCCenter for Space Research)提供的等时间段GRACE时变重力场质量反演结果替代,其中地心项和地球扁率项分别采用Swenson[21]和Cheng[22]结果来代替.对GRACE缺失月数据采用三次样条插值方法补齐.GRACE数据后处理采用的平滑方法为基于数据信噪特征的球面维纳滤波[23],并基于Wang[24] PGR模型扣除冰期后回弹因素的影响,最后对所需格点区域的陆地水储量时间序列做调谐分析,给出周年项、半年项和长期项拟合,拟合结果作为该区域的时变值.
|
图 1 非潮汐陆地水和海洋质量变化的周年振幅和位相 (a)(b)分别为陆地水质量变化的周年振幅和相位.(c)(d)分别为非潮汐海洋质量的周年振幅和相位.位相参考历元为2003年1月1日.(c)中白色部分为GRACE结果替代水文模式结果区域. Fig. 1 Annual amplitude and phase of the land water and ocean mass spatial variation Left is amplitude (unit: mmEQW, millimeter equivalent water height) while right is the phase (unit: dayofyear). We use the GRACE mass result instead of hydrological model in the white color area showed in (c). |
海洋质量的变化(表现为洋底压力OBP,Ocean Bottom Pressure)同样会引起重力场变化,反过来使海平面变化.为讨论非潮汐海洋负荷的影响,我们采用了麻省理工大学(MIT)的海洋环流数值模式资料ECCO估计的海水质量变化.ECCO模式是等体积守恒假设.网格经度从0°-360°纬度为80°S -79°N,经向网格为1°纬向网格从高纬度的1°到赤道区域的1°/3, 时间分辨率为12 h,这里采用算术平均方法得到月均值.需要指出的是,由于测高卫星海平面结果中已经包含了SAL的影响,我们选择的ECCO模式为未融合测高卫星资料的kf079版本.
3.3 大气水含量变化大气中水含量的变化也会对重力场有影响.空气中的干燥大气部分接近于常数,因此可以将全球地表的大气压强时变部分归结于大气中水含量的变化[25].本文采用的是美国国家环境气象中心NCEP/NCAR(National Centers for Environmental Prediction/National Center for Atmospheric Research)[26]的海平面气压数据.在大于2周时间尺度,海平面对大气压强变化的静态响应近似服从反变气压计原理IB[27] (InverseBarametor), 即每百帕的大气压变化对应于局部海平面升高或降低1 cm.这里我们对海洋上大气压数据进行了IB改正.
上面我们给出了水循环的三个主要组成成分及采用的数据模型.但是,任何一个单独的部分并没有考虑海洋与陆地或大气之间的水质量交换,因此总体质量未保持平衡.这里我们假设任何一个组成部分的总体水质量缺失将由海洋补偿,如(11)式中右边括号中第二项,其中Cmn为盆地函数的m阶n次球谐展开系数,
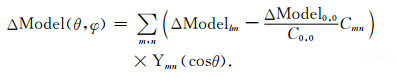
|
(11) |
但由方程(9)知该部分并不是均一薄层分布,方程(11)的结果只是作为循环迭代的初始值.为尽量避免球谐系数展开阶数小导致的截断误差和信号泄漏对结果的污染,在使用公式(1)之前,上述三种模型都插值为0.5°×0.5°.以2003年1月1日作为起始历元,以余弦函数为基底,用最小二乘方法拟合了各格点的周年项、半年项、常数项和趋势项.图 1显示了2003-2010年陆地水储量和非潮汐海洋经过质量守恒改正后的周年振幅和相位全球分布图.陆地水储量的周年变化显著区域为各大水流域,如印度恒河流域、非洲刚果河流域和亚马逊流域等.对应的周年相位空间变化比较简单,多出现在每年的10月(300°)或6月(180°)左右,由ECCO模式得到的海洋质量周年变化量级约为陆地水储量周年变化的30%,高纬度区域周年振幅相对中低纟韦度区域要大.除南大洋和一些沿海较浅区域外,由ECCO得到的海洋质量周年振幅不超过2 cm.周年相位大多数表现为流域尺度空间分布.除北太平洋亚热带环流区域外,太平洋和印度洋的多数区域周年相位保持一致,同时大西洋周年相位滞后太平洋区域约180°.
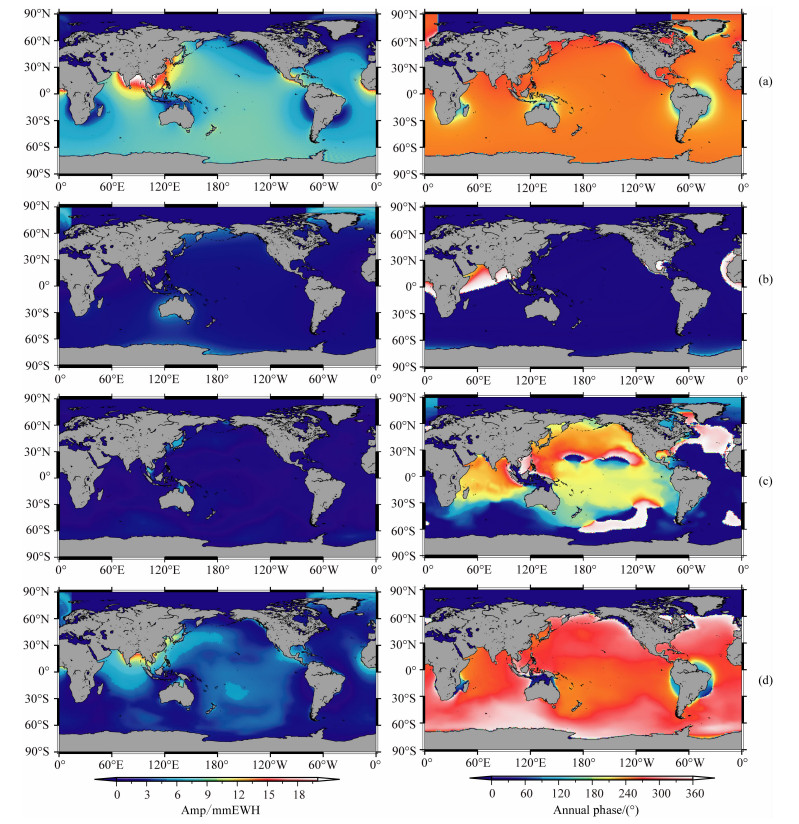
4 SAL对海平面变化的影响图 2a-2c给出了全球海平面SAL影响的周年振幅和相位的空间分布,包括陆地水储量变化、大气水含量变化和非潮汐海洋质量变化的单独SAL影响和三种因素联合SAL影响.为方便讨论,定义全球平均值(GMSL,Global MeanSeaLevel)为全球海洋网格以纬度余弦为权的加权平均结果.
|
图 2 (a)-(c)分别为CPC、NCEP和ECCO模型计算得到的SAL周年振幅和相位空间变化.(d)为综合变化. Fig. 2 (a)-(c) is annual amplitude and phase of the SAL effect under the individual model as CPC, NCEP and ECCO, respectively. (d) is their combination. |
SAL空间变化的主要驱动源为陆地水储量变化.陆地水储量变化的SAL效应在空间分布上不均匀,全球平均面积加权SAL周年振幅约为11 mm,周年振幅最大值为孟加拉东海岸区域,23.5 mm.振幅最小值为1.5 mm,主要为太平洋地区、阿拉斯加海湾和英属哥伦比亚等区域,只相当于全球平均值的14%.其它如印度洋区域,约为11 mm,大西洋区域约为9 mm.值得注意的是,在中国周边海洋区域,由该因素造成的海平面周年变化振幅约为13 mm,与ECCO模式得到的洋底压力周年振幅数值相当(图 1c),这可能是由该区域的复杂水文环境引起的.SAL周年纟韦度带分布极值出现在近赤道区域,且北半球比南半球要大得多,这与图 1b中的陆地水储量周年振幅最大值出现在北半球有关,当该区域水质量富集时,由于自吸引作用,周边海域的水质量也开始富集,因此出现最大值.相对于振幅空间分布而言,相位分布比较均一.陆地水储量的SAL效应只对近海的相位有所影响,远海区域最大值大多出现在每年的8-9月,物理机制与振幅相同.
大气质量变化的SAL影响小于陆地水储量,其振幅和相位空间分布比较单一(图 2b),对GMSL周年振幅影响约3.2 mm,相位26°.
相对于陆地水储量和大气质量的SAL影响,海洋引起的SAL对全球海平面变化的影响振幅强度约为陆地水SAL影响的20%,振幅空间分布较为简单.由假设知海洋SAL对全球海平面振幅的面积加权平均值为零.尽管如此,仍具有显著的地理空间变化特征(图 2c).最大值出现在中国南部海域和澳大利亚的卡奔塔利亚湾,振幅约为9 mm,在印度洋海域约为4 mm.图中的许多高值区域也为其它文献所证实[9].对比振幅空间分布而言,空间相位变化要复杂得多,具有很强的区域性:太平洋周年相位180°~360°印度洋190°~320°白令海330°~360°.由此因素引起的SAL周年相位在中国南海区域和东海(包括渤海)区域存在显著的相位差,南海滞后约2个月,这可能是由该区域复杂的海洋洋流环境引起的.
图 2d给出了大气、非潮汐海洋和陆地水储量总体SAL对相对海平面变化的周年振幅的影响.结果显示SAL空间变化特征与Clarke[6]分析结果类似,振幅波动范围从1.5 mm至18 mm.在北美、欧洲、亚洲北部、刚果河和亚马逊河流域周边海岸,SAL周年振幅低于全球平均值.在南部太平洋中心海岛区域和非洲西海岸区域、太平洋东南部,振幅显著高于全球平均值.在孟加拉湾区域可以达到两倍量级.因此在这些区域,当融合实际观测数据至海洋模型时必须考虑SAL的影响.值得注意的是,当孟加拉国在雨季洪水爆发时,SAL对附近的孟加拉海湾海平面影响达到最高值.相对于陆地水储量单独的SAL影响,总体SAL对海平面变化的周年振幅影响要小一些,这是因为大气SAL引起的海平面变化的周年相位滞后140。于对应的陆地水储量结果(图 3).
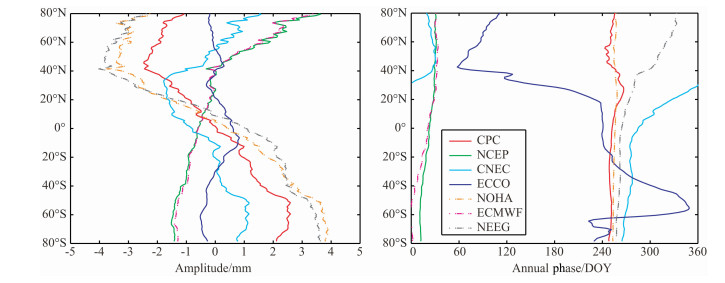
|
图 3 CPC、NCEP、ECCO、NOHA、ECMWF模型SAL影响的周年振幅(扣除了全球平均值)和相位纬度带分布.CNEC(前三个模型总和)和NEEG(后三个模型总和)综合影响. Fig. 3 Zonally averaged amplitude (left) and phase (right) of SAL effects according to CPC, NCEP, ECCO, NOHA and ECMWF model. CNEC (Sum of the former three models) and NEEG (Sum of the later three model) is the combined effect. |
此外,受限于模型的理论完善程度和采用的实际输人数据缺乏等因素,大气、陆地水和海洋模型结果本身还有较大程度上的不确定性.同时GRACE的低空间分辨率和后处理中所用的滤波器影响使得GRACE估计得到的陆地冰质量具有较大的不确定性,这都会影响我们所计算的结果.为此我们基于另外一组模型数据给出了相应的SAL结果.水文模式采用美国宇航局NASA(NationalAeronauticsand SpaceAdministration)戈达德空间飞行中心全球陆地资料同化系统GLDAS[28]的NOHA模型.与3.1节类似,GLDAS中相应的冰川(盖)结果由德国地学中心GFZ(GermanResearchCenter forGeosciences)给出的GRACE时变解代替.大气压数据为欧洲中期天气预报中心ECMWF (European Centrefor Medium-Range WeatherForecasts)再分析资料.图 3给出了CPC(CSR)、NCEP、ECCO、NOHA(GFZ)和ECMWF单独和两种组合解(记CNEC为前三个模型总和,NEEG为后三个模型总和)的SAL影响的周年振幅和相位纬度带分布.可见CPC与NOHA振幅随纬度变化趋势非常一致,但振幅大小存在一定的差别,在近赤道区域两者差别最不显著.ECMWF与NECP在振幅空间和相位空间非常一致,差别非常小.联合解NEEG与CNEC结果空间分布较为一致,只是振幅略小,相位空间NEEG在北半球比CNEC超前约1个月,南半球差别较小.总体来看,陆地水储量模式是影响SAL结果的主要因素,不同模式组合的SAL效应对海平面变化的周年影响差异主要为振幅,对相位空间分布的影响较小.
5 对验潮站结果方差解释贡献由以上计算结果可知,SAL对沿海区域的海平面周年变化有显著影响,部分区域超过10 mm量级,应该可以由沿海的验潮站所观测.因此这里我们检验了在海洋洋底压力模型中加人SAL结果后是否与验潮站实际观测符合得更好,这通过对每个验潮站时间序列的方差解释贡献(VarianceReduction)来衡量.验潮站数据来自PSMSL[29]中心的RLR数据,包括425个验潮站点数据.要求各站点数据在2003-2010年间至少含85% (82个月)的月平均观测值,同时剔除地震等因素引起的突变站点.对验潮站得到的海平面高,首先基于NCEP气压模型进行反变气压计改正,然后采用Ishc[30]温盐模型进行比容海平面因素改正.假定剩余的验潮站点海平面变化时间序列均方差为σSL2,定义VR1和VR2分别为在ECCO海洋洋底压力模型中考虑SAL影响前后对验潮站剩余海平面变化时间序列的方差解释.AVR为前后解释方差之差.当其值大于零时表明引人SAL影响结果可以改善模型与实际观测的符合程度.定义:
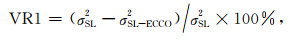
|
(12) |
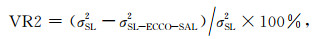
|
(13) |
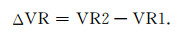
|
(14) |
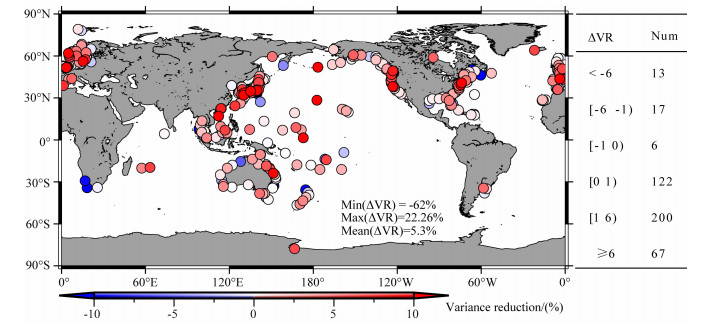
本文关注的为SAL周年变化,在计算ΔVR之前我们对各时间序列作0.5~1.5年的带通滤波.图 4给出了ΔVR大小在验潮站上的空间分布.全球平均解释方差比例为5.3%, 解释方差最大为22.26%, 最小值为-62%,超过90%的站点ΔVR为正值,不同的解释方差区间的验潮站点数见图 4右表.正的ΔVR显示出区域特征,在SAL周年项振幅较大的区域对应的ΔVR比较大,如日本周边东太平洋区域、欧洲北大西洋区域、北美东西海岸区域等.同时,在一些站点,如南非站点引入SAL影响后,模型结果反而与验潮站观测结果方差差别较大,但应注意到此类站点空间分布并不具备区域性,只表现为空间零散分布.AVR为负,可能是由两方面的因素引起的:一方面是由于所采用的温盐改正模型在这些区域缺少足够多的时间观测,且可能含有其它气候因素的影响未被改正;另一方面是该区域的海平面变化自身变化幅度相当小(见图 1中ECCO周年振幅空间分布),即使引入的SAL附加信息量非常小,对方差改变也非常大.该检测结果显示,在ECCO海洋模式的洋底压力模型中包含SAL的影响可以使得模型值与验潮站观测值符合得更好,有助于更好地理解海平面季节变化的物理机制.
|
图 4 左图:在ECCO洋底模式中引入SAL影响前后对验潮站非比容海平面变化解释方差之差ΔVR(方程(19)).右表:ΔVR各区间的站点数 Fig. 4 Left: Percentage variance reduction in the time series after adding SAL effect to ECCO OBP model(Eq.(19)). Right: number of the tide gauges according to different ΔVR |
陆地、海洋和大气之间的水质量交换,通过SAL效应都可以引起全球海平面时空重分布变化.考虑自吸引效应和旋转离心力位的影响,基于海平面方程,我们分别解算了陆地水储量、非潮汐海洋、大气中水质量重分布对全球海平面变化的影响,同时也解算了综合影响.结果显示质量迁移引起的SAL效应对全球海平面周年变化有显著影响,具有显著的空间变化特征.在三种SAL激发源中,陆地水储量变化周年SAL振幅最大,大气因素次之,非潮汐海洋影响最小,但非潮汐海洋的周年SAL相位空间分布最为复杂.在许多区域综合SAL影响周年振幅达到10~20 mm量级,与海洋动力学因素导致的海平面周年变化相当,在近海岸区域尤为明显,这使得在解释观测得到的海平面高度周年变化时考虑SAL的影响非常重要.如在阿拉斯加湾、孟加拉湾和刚果河流域周边SAL周年振幅空间梯度变化最为明显,且周年振幅大于10 mm,大于洋底压力仪记录噪声水平(0.5~1 mm)[31],因此在这些区域可以使用洋底压力记录进行验证.除在几个主要的水文流域附近海域外,南半球的SAL周年振幅比北半球要大.
值得注意的是,不同的模式及其组合解算的周年SAL空间分布差别较小(图 3),但振幅差别较大,尤其是陆地水文模式的周年SAL影响.这一方面是由于水文模式的内在不足,如缺少有效地下水时变信息等造成的.另一方面不同的GRACE数据中心公布的时变重力场信噪比也不同,对不同GRACE数据源采取相同的数据处理方式可导致差别较大的冰川质量时变结果.即使对同一数据中心,不同的数据后处理方法得到的结果振幅差别也较为明显,这都会使得采用不同的数据源得到的SAL周年振幅具有较大差异.尽管如此,对比验潮站数据,在考虑热盐比容变化、IB响应和冰期后回弹的基础上,在ECCO海洋洋底模型中引人SAL影响可以额外解释约5.3%观测信号.另外由于SAL的振幅及梯度相对热盐比容因素引起的周年海平面变化而言较小,在测高卫星观测得到的海平面变化中扣除热盐比容影响部分后,在远海区域的测高卫星结果中检测SAL信号将极具挑战性.这在下一步的工作中将详细论述.
致谢感谢汪汉胜研究员在本文完成过程中给予的帮助.
| [1] | Tsimplis M N, Woodworth P L. The global distribution of the seasonal sea level cycle calculated from coastal tide gauge data. J. Geophys. Res. , 1994, 99(C8): 16031-16039. DOI:10.1029/94JC01115 |
| [2] | Cazenave A, Dominh K, Guinehut S, et al. Sea level budget over 2003-2008:A reevaluation from GRACE space gravimetry, satellite altimetry and Argo. Global and Planetary Change , 2009, 65(1-2): 83-88. DOI:10.1016/j.gloplacha.2008.10.004 |
| [3] | Hill E M, Ponte R M, Davis J L. Dynamic and regression modeling of ocean variability in the tide-gauge record at seasonal and longer periods. J. Geophys. Res. , 2007, 112(C5): C05007. |
| [4] | Ponte R M, Quinn K J, Wunsch C, et al. A comparison of model and GRACE estimates of the large-scale seasonal cycle in ocean bottom pressure. Geophys. Res. Lett. , 2007, 34(9). DOI:10.1029/2007GL029599 |
| [5] | Holgate S J, Woodworth P L. Evidence for enhanced coastal sea level rise during the 1990s. Geophys. Res. Lett. , 2004, 31(7). DOI:10.1029/2004GL019626 |
| [6] | Clarke P J, Lavallee D A, Blewitt G, et al. Effect of gravitational consistency and mass conservation on seasonal surface mass loading models. Geophys. Res. Lett. , 2005, 32(8). DOI:10.1029/2005GL022441 |
| [7] | Woodward R S. On the form and position of mean sea level. US Geol. Surv. Bull. , 1888, 48: 87-170. |
| [8] | Farrell W E. Deformation of the Earth by surface loads. Reviews of Geophysics , 1972, 10(3): 761-797. DOI:10.1029/RG010i003p00761 |
| [9] | Tamisiea M E, Hill E M, Ponte R M, et al. Impact of self-attraction and loading on the annual cycle in sea level. J. Geophys. Res. , 2010, 115(C7). DOI:10.1029/2009JC005687 |
| [10] | 汪汉胜, 王志勇, 袁旭东, 等. 基于GRACE时变重力场的三峡水库补给水系水储量变化. 地球物理学报 , 2007, 50(3): 730–736. Wang H S, Wang Z Y, Yuan X D, et al. Water storage changes in Three Gorges water systems area inferred from GRACE time-variable gravity data. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 730-736. |
| [11] | 钟敏, 段建宾, 许厚泽, 等. 利用卫星重力观测研究近5年中国陆地水量中长空间尺度的变化趋势. 科学通报 , 2009, 54(5): 816–821. Zhong M, Duan J B, Xu H Z, et al. Trend of China land water storage redistribution at medi-and large-spatial scales in recent five years by satellite gravity observations. Chinese Sci. Bull. (in Chinese) , 2009, 54(5): 816-821. |
| [12] | Velicogna I, Wahr J. Acceleration of Greenland ice mass loss in spring 2004. Nature , 2006, 443(7109): 329-331. DOI:10.1038/nature05168 |
| [13] | Chen J L, Tapley B D, Wilson C R. Alaskan mountain glacial melting observed by satellite gravimetry. Earth Planet. Sci. Lett. , 2006, 248(1-2): 368-378. DOI:10.1016/j.epsl.2006.05.039 |
| [14] | Clark J A, Farrell W E, Peltier W R. Global changes in postglacial sea level:a numerical calculation. Quaternary Research , 1978, 9(3): 265-287. DOI:10.1016/0033-5894(78)90033-9 |
| [15] | Milne G A, Mitrovica J X. Postglacial sea-level change on a rotating Earth:first results from a gravitationally self-consistent sea-level equation. Geophys. J. Int. , 1996, 126(3): F13-F20. DOI:10.1111/gji.1996.126.issue-3 |
| [16] | Kendall R A, Mitrovica J X, Milne G A. On post-glacial sea level-Ⅱ. Numerical formulation and comparative results on spherically symmetric models. Geophys. J. Int. , 2005, 161(3): 679-706. DOI:10.1111/gji.2005.161.issue-3 |
| [17] | Spada G, Stocchi P. SELEN:A Fortran 90 program for solving the "sea-level equation". Computers & Geosciences , 2007, 33(4): 538-562. |
| [18] | Han D, Wahr J. Post-glacial rebound analysis for a rotating Earth. Geophysical Monograph Series , 1989, 49: 1-6. |
| [19] | Milne G A, Mitrovica J X. Postglacial sea-level change on a rotating Earth. Geophys. J. Int. , 1998, 133(1): 1-19. DOI:10.1046/j.1365-246X.1998.1331455.x |
| [20] | Fan Y, van den Dool H. Climate Prediction Center global monthly soil moisture data set at 0.5° resolution for 1948 to present. J. Geophys. Res. , 2004, 109(D10): D10102. DOI:10.1029/2003JD004345 |
| [21] | Swenson S, Chambers D, Wahr J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. , 2008, 113(B8). DOI:10.1029/2007JB005338 |
| [22] | Cheng M K, Tapley B D. Variations in the Earth's oblateness during the past 28 years. J. Geophys. Res. , 2004, 109(B9). DOI:10.1029/2004JB003028 |
| [23] | Sasgen I, Martinec Z, Fleming K. Wiener optimal combination and evaluation of the Gravity Recovery and Climate Experiment (GRACE) gravity fields over Antarctica. J. Geophys. Res. , 2007, 112(B4). DOI:10.1029/2006JB004605 |
| [24] | Wang H S, Wu P. Effects of lateral variations in lithospheric thickness and mantle viscosity on glacially induced relative sea levels and long wavelength gravity field in a spherical, self-gravitating Maxwell Earth. Earth Planet. Sci. Lett. , 2006, 249(3-4): 368-383. DOI:10.1016/j.epsl.2006.07.011 |
| [25] | Trenberth K E, Fasullo J, Smith L. Trends and variability in column-integrated atmospheric water vapor. Climate Dynamics , 2005, 24(7-8): 741-758. DOI:10.1007/s00382-005-0017-4 |
| [26] | Kalnay E, Kanamitsu M, Kistler R, et al. The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteor. Soc. , 1996, 77(3): 437-471. DOI:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2 |
| [27] | 闫昊明, 朱耀仲. 全球海平面对大气压变化的响应. 地球物理学报 , 2001, 44(3): 320–326. Yan H M, Zhu Y Z. Response of sea level to variation of atmospheric pressure. Chinese J. Geophys. (in Chinese) , 2001, 44(3): 320-326. DOI:10.1002/cjg2.v44.3 |
| [28] | Rodell M, Houser P R, Jambor U, et al. The global land data assimilation system. Bull. Amer. Meteor. Soc. , 2004, 85(3): 381-394. DOI:10.1175/BAMS-85-3-381 |
| [29] | Woodworth P L, Player R. The permanent service for mean sea level:An update to the 21st Century. Journal of Coastal Research , 2003, 19(2): 287-295. |
| [30] | Ishii M, Kimoto M. Reevaluation of historical ocean heat content variations with time-varying XBT and MBT depth bias corrections. J. Oceanogr. , 2009, 65(3): 287-299. DOI:10.1007/s10872-009-0027-7 |
| [31] | Eble M C, Gonzalez F I. Deep-ocean bottom pressure measurements in the northeast Pacific. J. Atmos. Oceanic. Tech. , 1991, 8(2): 221-233. DOI:10.1175/1520-0426(1991)008<0221:DOBPMI>2.0.CO;2 |
 2013, Vol. 56
2013, Vol. 56

