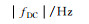合成孔径雷达差分干涉测量(D-InSAR)是最近二十余年发展起来的一项极具潜力的空间对地观测技术[1],它通过SAR传感器两次回波信号的相位差和卫星轨道参数反演地球表面的微小变化,其精度可以达到厘米级[2-3].该技术凭借SAR系统具有光学传感器无法比拟的全天时、全天候的成像特点,已被广泛应用于形变监测领域,其主要研究集中在地震监测、震后形变测量、火山运动、地面沉降、冰川漂移以及山体滑坡等方面[4-8].
虽然目前D-InSAR技术在理论、数据源等方面已经日趋成熟,但在实际观测和数据处理过程中,仍有许多因素制约了常规D-InSAR技术及其衍生方法(PS-InSAR方法、小基线D-InSAR方法等)的运用,主要体现在可监测的形变量级和形变提取的精度上.一方面受传感器自身特点和地表形变特征的相互关系制约,比如当研究区域的地表位移过大时(如断裂带周围的形变)无法使用D-InSAR技术进行量测,当地表沉降的速率非常缓慢时其它相位分量(如大气,噪声)掩盖了形变相位等;此外,雷达侧视成像机理容易引起影像上的叠掩和阴影,遮蔽有用的形变信息,而传感器参数如人射角、波长等也在不同程度上影响着相位对形变的敏感度,使得形变信息无法准确提取.另一方面,干涉失相关和大气作用也是影响形变提取精度的关键的两个因素,它们造成的误差可能达到厘米级甚至更高[9-10].
上述制约从D-InSAR机理和数据处理本身来说是难以克服的,这些限制因素不仅影响了差分干涉测量技术在形变监测中的实际应用,而且潜在地造成了大量人力资源、财物和时间的浪费.因此,开展干涉条件分析,探讨这些因素在D-InSAR技术的实际应用中产生多大的影响以及如何影响,具有重要理论意义和实用价值.
基于当前在InSAR约束条件和量化分析方面研究尚少的现状,本文将系统阐述影响InSAR形变监测的几个关键因素,着重量化分析与传感器参数相关的几个分量(人射角、波长、影像分辨率、系统带宽等)对实际观测的影响,进而比较各传感器的监测能力,并以此为依据推出具有一般性的结论,即各传感器临界坡度范围以及它们可监测到的最大形变量.另一方面,在相关章节分析了现有与SAR干涉限制有关的两个模型,并对其进行有针对性的修正和完善.最后,采用模拟数据和真实数据对本文结论进行验证.本文的研究将为建立更加完善的InSAR干涉限制数学模型提供有力的依据,有助于研究感兴趣区域时的数据选择和参数配置,提高D-InSAR的应用效率.
2 D-InSAR干涉条件分析InSAR技术只有在成像期间两次回波信号相干的条件下才能正常工作,这是干涉本质,也是干涉测量的最基本条件[9-11].相干性的丢失,即失相关作用,使得该技术无法正常反演地球物理特性变化和提取地表特征[12].影响去相关的因素有很多,主要包括两次成像期间散射体物理分布的变化(时间去相关)、两次观测位置的变化(空间去相关)、成像区地貌特征、地球物理活动以及数据处理(如影像插值、配准)等.其中,时空去相关和地表特征对SAR干涉的限制最为重要并且是不可逆的过程[10].因此,通过定量地分析这些因素与干涉测量的关系,并采取有效的措施减小或避免这种约束是十分必要的.考虑到去相关作用和地表属性特征对SAR干涉限制的重要性,本文将研究重点集中在这两个方面,并着重探讨它们对形变监测的影响.
2.1 空间去相关空间去相关是两次成像时雷达以不同的人射角照射地物目标引起的结果,其数学定义为

|
(1) |
从式(1)可以看出,总的去相关由两部分组成:(1)面散射去相关分量;2)体散射去相关分量.其中面散射可以较好地从频域上分析:即由于不同视角的观测导致不完全相同的地面反射谱,两次观测的目标谱响应之间存在相对偏移,从而造成了回波信号不完全一致,互相关小于1.而体散射涉及电磁波的穿透性,与雷达波长和散射体大小有很大的关系.在高穿透性区域,如植被覆盖区(森林、农作物)和冰川累积区,体散射去相关较面散射去相关占据主导位置[13-14].
2.1.1 面散射去相关有关面散射去相关的介绍在很多文献中都有详细论述[9, 15-17],但这些研究都主要集中在几何基线对干涉相干性的影响.采用频域滤波技术,因基线引起的几何去相关可以被消除.然而当成像区的地势有起伏时,局部坡度也会对空间去相关产生贡献,在某些区域(如阴影处)甚至造成信号完全丢失.因此,坡度对D-InSAR的限制非常明显并具有不可逆性.
虽然优化或滤波处理能够降低噪声,恢复形变信号,但是信号盲区完全取决于地形特征以及SAR系统参数,这些区域的形变仍然无法恢复.因此,在对感兴趣的地区进行研究之前,统计分析地形特征和现有卫星参数可以最小化D-InSAR监测的限制.
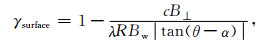
|
(2) |
其中,c是光速,θ是入射角,α代表局部地形坡度角,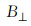
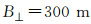
|
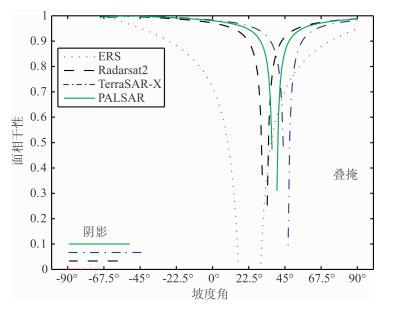
图 1 面散射去相关与地面坡度的关系 Fig. 1 The relationship between surface scattering decorrelation and ground slope |
总体而言,面散射相干性随坡度角逐渐靠近雷达入射角呈指数衰减.这种现象可以解释为当入射波与坡度逐渐形成垂直关系时(θ=α),地距分辨率单元无限增大,导致所有细节丢失,形成完全去相关[18].因此,对于每一个传感器,都存在一个临界坡度范围(图 1中关系曲线的缺口),它是传感器参数和垂直基线的函数.当γsurface=0, 对式(2)进行简单的转换之后,可以获得临界坡度的范围:
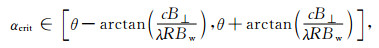
|
(3) |
由式(3)可以得到一系列临界坡度值:ERSαcrit∈[16.2°, 29.8°]; Radarsatαcrit∈[1.6°,33.6°]; TerraSAR-Xαcrit∈[44. 9°, 46.9°]; PALSARαcrit∈[37.8°,39.6°].虽然上图中表现出丘尺3的抗地形去相关能力总体最弱,并且盲区跨度最大达13.6°, 但此结论并不适用于所有条件.比如当44. 9°≤α≤46.9°时,ERS的γsufce接近0.8, 而TerraSAR-Xγsufce为0.式(3)还表明无论任何传感器,垂直基线都表现出负作用,即盲区随着垂直基线的增加而增加,这一作用必须通过传感器参数进行补偿.由于TermSAR-X系统的频率带宽是其它传感器的近10倍(见表 1),它补偿了短波容易引起面散射去相关的不足,并表现出总体上最强的抗去相关能力.
|
|
表 1 模拟参数 Table 1 The parameters of simulations |
同时本文还模拟了各个传感器出现阴影的地形坡度范围,即-90° < α < θ -90°由于中心入射角较小,在崎岖地形的监测上,ERS影像可以获得更少的阴影区域.
综上所述,面散射去相关在不同传感器下差异明显,但并不能以此得出新一代的传感器在监测地表形变时就一定能够获得更高的相干性,还需要考虑地形坡度.因此,对于任意研究区域,研究人员可根据先验信息如SRTM DEM计算该区域的坡度角,再对其进行直方图分析,得到坡度角的空间分布特征,最后结合式(3)选择最理想的传感器数据.
2.1.2 体散射去相关理论上,植被覆盖区的体散射去相关模型可以表示为[19]
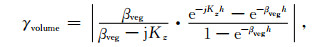
|
(4) |
其中,βveg表示植被的二维透射率(反映植被稀疏程度)h表示植被厚度(或植被高)Kz与雷达系统有关: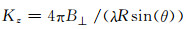
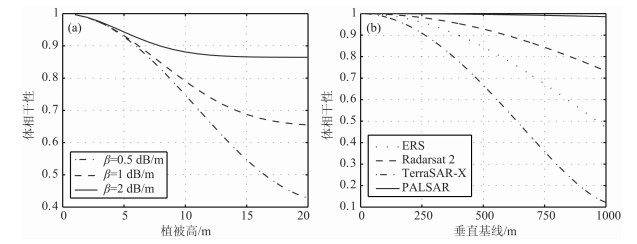
图 2a是当垂直基线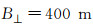
|
图 2 体散射去相关与植被高(a)及垂直基线(b)的函数关系 Fig. 2 The functional relation between volume scattering decorrelation and vegetation height(a), The functional relation between volume scattering decorrelation and perpendicular baseline(b) |
而图 2b则表明了体去相干和垂直基线的函数关系,为凸显各个传感器在去相干能力上的差异,本文根据4颗卫星的参数分别进行了模拟实验(参数详见表 1).选取的地表参数为:植被高h=6 m,透射率βveg=0.5dB/m.图中体相干性随垂直基线的增加逐步衰减,衰减速度随波长的增加而减小.这一结果说明,较其它传感器参数而言,波长的大小在体散射去相干中占据主导地位.由于微波会与波长数量级大小的散射体发生作用,波长较短的X波段较L波段更容易与散射面进行交互,发生体散射.结合图 2a可知,随着植被厚度的增加和透射率的减小,图 2b中的体相干性呈变化率更大的整体衰减趋势.
以上分析表明在体去相关主导的区域如植被和雪地,仅考虑面散射去相关分量的相干性分解模型[17]不足以提取时间去相关分量,而该分量对于理解实验区的SAR干涉限制有着重要的作用[20].基于此,本文在现有研究基础上对模型进一步推广,加入体去相关分量,使得时间去相关建模成为可能.
对于分布式的目标,总体去相关可以表示为[10]
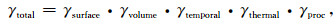
|
(5) |
其中,γproc为数据处理去相关,γtemporal为时间去相关,γtemporal为热噪声去相关.一般来说,γproc和γtemporal非常小,在实际观测中可以忽略不计,则观测的相干图可以表示为

|
(6) |
可由式(4)直接推出体去相关分解模型的一般形式,但是(4)式在应用中有两个限制:(1)表达十分复杂,从而得到的模型复杂,并且仅仅适用于植被区域的情况;(2)透射比βveg和树高h在无实地数据的情况下很难获得,推广模型在实际应用中无法实现.因此,本文采用具有更一般性的体散射模型[15, 18]:
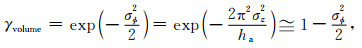
|
(7) |
其中,σφ和σz分别代表相位标准差和分辨率单元内的高程标准差,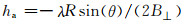
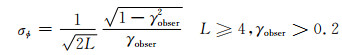
|
(8) |
其中,L表示有效视数.最后,联合式(6),(7),(8)和(2)相干性分解模型可以进一步完善并获得近似的时间去相干分量:
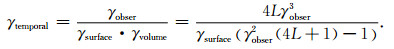
|
(9) |
上文已经提到失相关作用是限制差分干涉测量的一个重要因素,它是雷达系统参数和地物属性的函数.另一个与干涉条件相关的分量涉及地物目标的相对偏移量,可以用形变梯度进行描述,它是地壳运动的结果.由于In SAR技术只能监测到沿视线方向的地表形变,而实际的地表运动往往比较复杂.因此,若想利用In SAR观测来完整地描述形变梯度是十分困难的.作为折中,地物两点之间相对偏移量的大小往往通过差分干涉图的相位梯度来衡量.相位梯度是指在SAR坐标系下,影像任意两点相对位移差Δγ与两点距离(斜距差ΔSR)的比,其中Δγ由两个目标间的条纹数确定.由于条纹率与波长成反比,可得相位梯度与雷达系统本身的参数有关,而形变梯度并不取决于雷达参数的属性.
由此可以建立形变梯度与相位梯度之间的函数关系.如图 3表示了相邻两像素对卫星的几何关系,其中,θ为主影像入射角,ΔGR为相邻两像素O点和P点的地距差,Δd代表了垂直于地表的变形(隆起).为便于推导,本文假设了形变只沿着PP ′方向发生,且O点无变形.根据图 3可知地表形变梯度为而影像的相位梯度/可以表示为
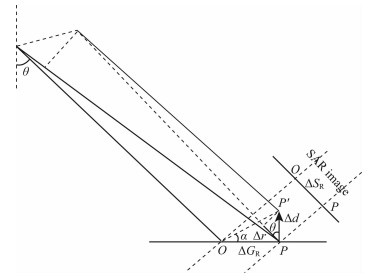
|
图 3 SAR成像局部几何示意图 Fig. 3 Geometry of SAR imaging |
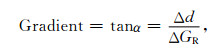
|
(10) |
而影像的相位梯度f可以表示为
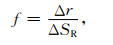
|
(11) |
考虑斜距与地距的几何关系Δr=cosθ·Δd以及ΔSR=ΔGR · sinθ,形变梯度与相位梯度的函数关系可表示为
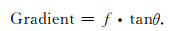
|
(12) |
这里,对于正在运行的SAR传感器,除TerraSAR-X外(中心入射角45.9°),均有Gradient < f.
式(12)扩展了已提出的形变梯度模型[21],它不但为模型引入了新的参数(入射角),完善了模型,而且可以更为精确地预报研究区是否适合用InSAR进行监测.形变梯度需要先验地由外部数据获得,然后再带入模型进行解算,从而获取预报结果,而GPS等数据测得的任意两点的梯度Gradient与模型相位梯度f存在偏移量tanθ如果直接将Gradient带入模型则使得模型的预报精度降低.Massonnet等[12]提出的InSAR可检测的最大形变梯度(实质上是指相位梯度)为一个像素只能有1个干涉条纹的位移存在,携带不同中心频率的SAR传感器检测到的最大形变梯度范围差异十分明显,如ERS为3×10-3,PALSAR为13×10-3.大于该量级的形变梯度将产生相位混叠,或者说,由于波谱偏移f大于SAR影像距离向带宽,导致两个目标谱的零重叠,引起信号完全去相干.另一方面,最小可检测到的形变梯度在约10-7量级,小于该量级梯度的相对形变将被大气、轨道误差等掩盖.需要指出的是,以上的结论前提是相干性为1,但在实际应用中,由于干涉噪声存在,InSAR的监测能力远远达不到理论值[22].即使在理想情况下的监测,干涉数据处理(多视处理、相位解缠)也限制了可检测的形变梯度范围[23].从最新的研究来看[21] InSAR监测形变量级的能力随着相干性的减小而减小,随着视数的增加最大可检测的形变梯度减小,最小可检测的形变梯度增加.这一结论说明InSAR形变监测的能力与数据处理技术是密不可分的.
3 模拟实验第2节剖析了限制D-InSAR干涉的两个关键因素.在它们的影响下,不同传感器的形变监测能力差异明显.为了更好地理解这些因素在真实干涉图中是如何制约形变量的提取,并验证上文提出的结论,本节根据各个传感器系统参数和地表特征进行了有针对性的仿真实验,以下研究所需系统参数均列于表 1.
第一个实验将用于说明形变梯度对差分干涉测量的影响,并进一步推断各传感器可监测到的最大地表形变量.Okada模型被用来模拟空间尺度为1km×2km(距离向×方位向),运动方向为垂直于地表的形变,即垂直形变,其中最大位移靠近断层(黑色虚线),量级达到0. 5 m.为突出形变量(或形变梯度)对InSAR的限制,本例中相干性假设为1,且没有考虑大气和轨道误差.
从图 4可以看出同一形变量在不同系统影像上的差异.首先,整体上,由于大的变形梯度,密集的干涉条纹均集中在断层附近.其次,ERS,Radasat2和TermSAR-X的相位图出现高条纹率,而PALSAR条纹率较低,这主要是由波长决定的.波长越短,一个条纹(2π)对应的形变越小,相位对形变越敏感,反之亦然.最后,注意到ERS差分条纹在断层附近出现了相位不连续,而Radarsat2也产生了局部相位混叠,这与条纹瞬时频率fi和影像分辨率有关.相位混叠是欠采样的直接结果,低分辨率SAR影像的采样频率较低,在位移突变处很容易引起相邻相位离差激增,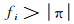

|
图 4 各传感器系统参数下的差分干涉图 Fig. 4 The differential interferograms for different sensors |
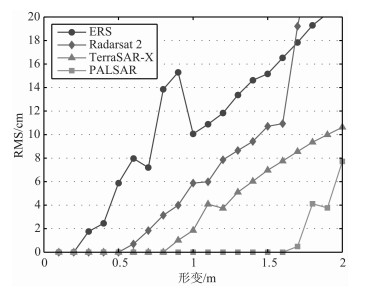
图 5是对上述实验的定量描述.由于相位混叠会引起InSAR测量误差增加,因此我们首先将形变量由0至2m递增,在每个形变量下分别模拟各个传感器的差分图,将它们作为InSAR观测到的结果,最后将其相位解缠后与原始形变进行比较.假如恢复后的形变与原始形变差异很小,我们认为该形变量可以被InSAR监测到,反之则认为该量级无法用InSAR进行监测.将测量误差RMS表示成形变量的函数,可以清楚地得知各传感器量测的最大形变量.从图 5可知,随着形变量的增加,D-InSAR监测形变的能力逐渐减弱.ERS传感器监测剧烈地表运动的能力最差,PALSAR最强.在0到2 m的形变量级中,TeraSAR-X和PALSAR可将测量精度维持在厘米级.此外,从图中还可以得到不同传感器监测地表的临界形变量,分别为:dERS=0.2 m, dRadarsa2=0.5 m,dTerraSAR-X=0.8 m,dPALSAR=1.6 m,超过阈值的差分图将出现相位混叠.最后需要注意的是,图 5中ERS模拟序列产生的不连续性是由最小费用流解缠引起的,重复实验将有助于消除这一跳变.
|
图 5 不同传感器参数条件下的形变提取误差分布图 Fig. 5 The error distribution map of deformation extraction for different sensors |
虽然L波段可以监测到较大的形变,但SAR成像几何和坡度角的作用进一步限制了形变监测.根据2.1. 1节提及的内容,通过位于Enta地区的ASTER高程数据和ALOS传感器参数模拟了此类限制,其中干涉图的每个条纹对应了11. 8 cm的视线向形变.
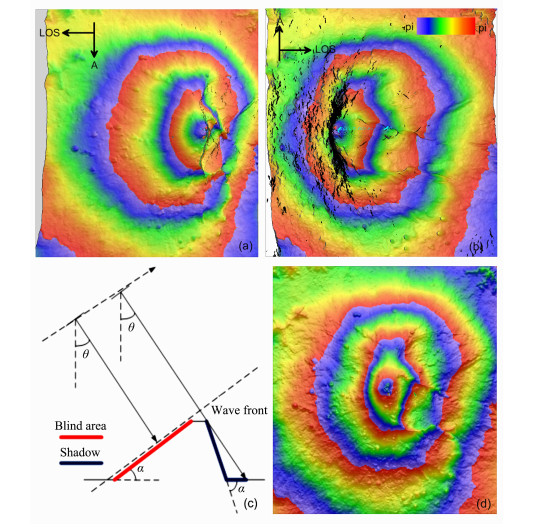
图 6为模拟结果,假定卫星沿着正北或正南方向飞行.其中图 6a表示了SAR传感器沿降轨方向的观测(SAR坐标系);图 6b表示传感器沿升轨方向的观测(SAR坐标系);图 6d表示地距影像(地距坐标系).可以看出,即使相干性为1,任何一次SAR观测都不能完全监测到地表形变.举例来说,对于降轨(升轨)影像,传感器不可能完整地观测到影像东边(西边)的形变.主要原因是在叠掩与阴影区,信号较弱或者无信号(详见2.1.1节).此外,当坡度角靠近雷达入射角时,影像分辨率无限增大导致信号失相关.在图(a,b)中,我们根据公式(3)用黑色散点标识了这些信号盲区,很明显升轨数据较降轨数据而言更不合适于该区域的形变监测,因为靠近西方向一侧的坡度更接近临界坡度αctit.若要获得该区域完整的形变图,解决方案之一是对升降轨干涉图进行数据融合,获得图 6d.
|
图 6 模拟的升降轨影像差分干涉图(a、b),地距向差分干涉图(d)以及SAR侧视几何(c) Fig. 6 Simulated differential interferograms for ascending and descending data (a) (b) differential interferograms in ground range (d) Geometry of side-looking SAR(c) |
上述2个实例分别从形变梯度和SAR几何两个方面阐述了SAR干涉限制,并同步验证了第2节中的内容.然而,这些实验中均假设了相干性等于1,对于实际应用,还应考虑去相干作用这一关键因素.基于此,本文根据地表属性和传感器参数分别模拟了SAR在裸地和植被区的干涉约束.该实验考虑了第2节中提及的所有InSAR约束,包括SAR几何限制,面散射与体散射去相关作用和形变梯度.
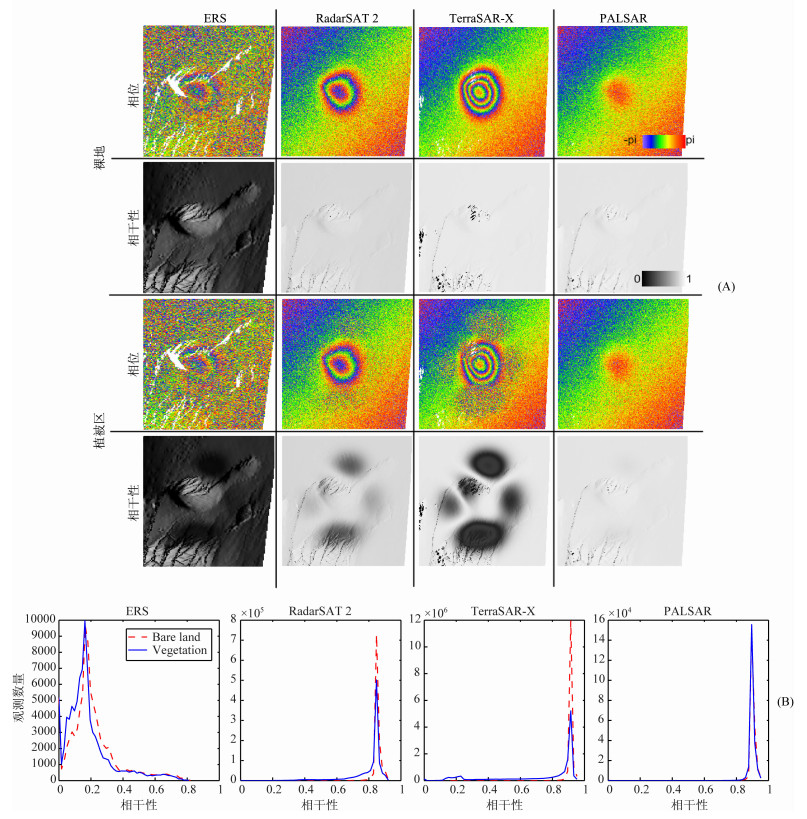
仿真采用的高程数据来自美国加州地区的一块分辨率为5m的样本数据.挑选相对平坦的一部分(2.6 km×4km)作为外部DEM.除了干涉噪声之外,本例还考虑了轨道误差,即跨越西北方向至东南方向的一个条纹趋势.形变被视为服从高斯模型的沉降漏斗,最大量级为5.6 cm,形变范围为2 km×2.5 km.植被高用peaks函数模拟,最大树高约10 m,透射比为0.5 dB/m.两个传感器的垂直基线假设为800 m.根据卫星几何、系统参数以及DEM相对位置模拟了相干图、相位图之后将它们投影至斜距向,结果如图 7A所示.
|
图 7 (A)裸地和植被区的各传感器差分干涉图及其相应相干图;(B)裸地和植被区各传感器影像相干性直方图 Fig. 7 (A) The different ialinterferograms and corresponding coherence maps for bare land andvegetation area (B) The coherence histograms of each sensor for bare land and vegetation area |
无论从目视还是量化的直方图(图 7B)来看,SAR在裸地区域的形变监测要明显好于植被区,整体相干性较高,但是各个传感器在同一地区的监测结果差异却非常大.在裸地地区,ERS的干涉相干性最差(mean=0. 21),Radarsat2次之(mean=0.83),TerraSAR-X最好(mean=0. 91).该结果与2.1. 1节的分析十分吻合,其主要原因为系统带宽和垂直基线.然而,TeraSAR-X的相干图上出现了一些相干性为零的区域,这些区域的平均坡度为45°,对应着临界坡度.而植被区的相干图,由于冠层和树茎的体散射作用,相干值发生了整体衰减.其中衰减速度最快的是TerraSAR-X(对照图 7B),平均相干性降至0. 72.相反,由于高穿透能力,这一体散射去相关作用在PALSAR相干图中并不明显(仅相差0. 004).在这两个区域中,干涉图质量最差的是ERS影像,这是因为模拟的垂直基线超出了ERS的临界基线.在其它传感器的影像中,这一长基线作用引起的相干性丢失因较大的系统带宽而得到了补偿(见表 1).
在形变量较大的情况下,由相干性分析和第一个实验结果可知,PALSAR数据对于任意地表类型都有较好的监测能力.然而,根据相位对形变的敏感度可知长波段提取形变精度低,对于微小形变,即使相干性很高,从模拟的干涉图中也不能准确地恢复精确的形变,尤其在大气或轨道误差存在的情况下.相反,此时短波长的数据优势比较明显,只要整体相干性不低于0. 3, 微小的形变就有可能被恢复[21].
综上所述,可以得出:1)在面散射占据主导地位的地区,TerraSAR-X传感器更合适监测微小形变如地表沉降.(2)在体散射占据主导地位的区域,Radarsat2等新一代C波段传感器更适合监测微小形变;当剧烈形变发生时,采用PALSAR数据监测效果最优.
4 真实数据分析第3节本文已采用模拟数据分析并验证了形变梯度和干涉相干性对不同SAR传感器的影响及其监测限制,并对指定的地表特征提出相应的策略来减小或避免SAR干涉的限制.在本节,我们将结合成像于三峡库区的ASAR和TerraSAR-X真实数据对相干性进行分析,从而验证2.1. 2节中的研究内容.
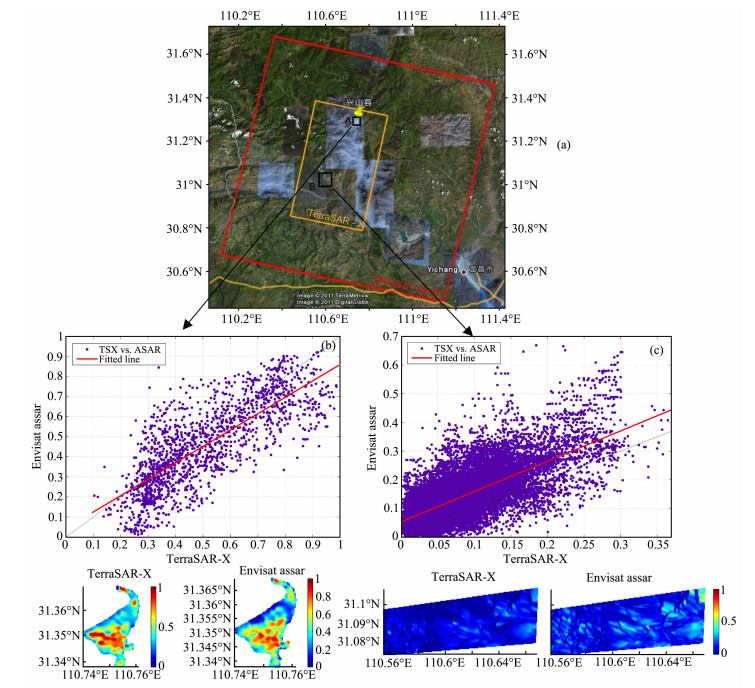
4.1 数据选择考虑到三峡库区地形起伏剧烈、空气湿度大,干涉去相干严重,该地区因此成为干涉限制分析最为理想的区域之一.本文选用的SAR数据覆盖范围、成像时刻气象资料和参数分别见图 8a和表 2.
|
图 8 (a)SAR数据覆盖范围;(b)A区域相干性分析及其所选取的相干值;(c)B区域相干性分析以及所选取的相干值 Fig. 8 (a) The coverage area of SAR data; (b) Coherence analysis and its coherence value in area A; (c) Coherence analysis and its coherence value in area B |
|
|
表 2 SAR干涉对参数 Table 2 The parameters of SAR interferometric pairs |
根据现有文献,时间作用是影响SAR干涉质量的最为关键的因素,这一作用因不同的地物类型而不同[9, 24-25].在植被区,时间去相关现象尤为复杂,相干性衰减迅速.基于这一点,若要客观评价或者量化分析位于三峡地区的不同平台数据的去相关作用,就需要尽可能地保证各干涉对在获取期间的外部条件相一致(至少成像时刻的气象瞬时变化必须基本吻合).因此,本文在进行数据选择时,参考了降雨量、温度和风速这三个决定时间去相关的关键指标(详见表 2),这三项指标是在研究去相关作用中主要被考虑的因素[9, 24-25].对于时间间隔较短的干涉对,这些气象资料主要影响着散射体表面的介电常数变化和散射中心随机运动状态.另外,根据三峡气象站的观测资料分析,该地区的年平均相对湿度保持在75%左右,我们假设这一因素在选择的数据中都具有相同的贡献.
4.2 数据分析按照地表类型的不同,本文从图 8a中的光学影像选择了两个子区域,它们分别代表了A:裸地和B:植被类型.这一实例分析将主要用于说明ENVISAT ASAR和Terrasar-X平台在不同地表上的监测能力,证明相干性分解技术必须加人体去相干分量估计,并同时验证观测结果是否与前述分析相吻合.
从表 2可知,分别代表了ENVISATASAR和Terrasar-X的No. 1和No. 2干涉对获取时间相近,成像时刻均为秋季.受限于卫星重返周期,两个干涉对时间基线的最小间隔为15d.基于No. 1和No. 2在各自成像时刻的气象资料基本相同,我们可以假设各干涉对的相干性具有相同的瞬时去相关分量γs; 如果将成像期间的时间相干性损失看作是随时间变化的线性函数γ1,那么本例中总的时间去相关γT=γs · γ1有如下关系:
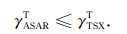
|
(13) |
又因为两个平台的垂直基线近乎相等,并且这一基线的量级对两个干涉对的面散射去相关分量基本不产生影响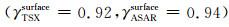
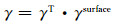
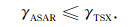
|
(14) |
在图 8b中,从两景相干图中分别提取了位于A区兴山县的公共部分,这一相干值观测通过自适应的相干性估计[26],并由有偏估计矫正后获得[27].从图上被提取的部分可以明显看出,No. 2的相干值比No. 1的稍高.我们将相同地理位置的同名点绘制成散点图后进行线性回归,回归线(红色)落在更偏向于X轴(Terrnsar-X)的位置,说明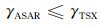

采用相同的方法,本文还分析比较了位于植被区B的公共部分.从提取的图 8c来看,No. 1的相干性明显高于No. 2, 回归线完全偏向Y轴(ENVISAT ASAR).这一结果似乎不符合公式(13)和(14)的判断.在ASAR具有更多的时间相干性损失和几乎相同的面散射相干性损失的前提下,B区的总体相干性γASAR > γTSX•然而,追溯至2.1.2小节的分析可知,本例中体散射去相干占据着主导地位,该分量的敏感性要远高于其它两者.这一实例,联合图 7中X波段的模拟实验表明,短波段的SAR传感器不适合植被区的干涉测量.此外,分析结果还显示了现有相干性分解模型有待完善,即相干性分解在植被区必须加人体散射分量γv,而不是仅考虑γT和γsurface两部分.这一结论可以再次进行验证:由于两个平台的广γsurface几乎相同,加之植被区ASAR数据的总体相干性γASAR较高,在去除γsurface后,如果不考虑体散射分量γv,时间相干性分量有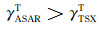
本文从地表属性、地形地貌、SAR系统参数以及形变特征四个方面详细阐述了InSAR技术在形变监测领域的干涉限制.通过大量的模拟实验和典型真实数据研究了这些限制对各个传感器的影响.本文所做出的贡献主要体现以下几个方面:(1)在面散射去相关作用的背景下,给出各传感器地表监测的信号盲区;(2)用定量的研究证明了体散射去相关作用对短波长传感器的重要影响,在此基础上对现有模型进行了完善和修正;(3)明确了形变梯度与相位梯度的差异,提出两者的函数关系,并将人射角引人形变梯度函数模型;(4)采用一系列具有代表性的模拟数据和真实数据对其进行了验证,验证结果显示实例分析和理论推断相符合.
另一方面,从本文研究中归纳得到了一些结论,这些结论有益于区域的数据选择.首先,对地壳运动较剧烈的地区(地震、火山、冰流),采用L波段的SAR数据较合适;对地表缓慢变形的研究(沉降),应该考虑C或X波段的数据;其次,任何一个形变都不能被InSAR技术完整地监测到,融合升降轨数据是解决途径之一.以图 6为例,监测位于影像西边(东边)的形变更适合采用降轨(升轨)数据.最后,在裸地区的地表监测中,TerraSAR-X系统具有最好的数据质量,并且对地表形变十分敏感,可以获得很高的精度;而在植被区,采用新一代C波段卫星数据更为合理,从图 7的实验结果来看,它在保证对形变提取精度的同时又兼顾了空间去相关作用.
虽然文中所研究的SAR系统参数仅为几种特定的工作模式,但它们都代表了各自传感器的主要特征,因此本文通过交叉验证和对比分析推导出的结论适用于大部分SAR系统数据处理.深人探讨InSAR技术在形变监测领域中的干涉限制问题,可为干涉处理配置提供辅助信息并根据形变特征选择最合适的数据,有效地推动了D-InSAR技术的实际应用,实现对地表形变的大面积、低成本和高效监测,具有重要的应用价值和实际意义.与此同时,本文的研究内容不仅可应用在地表形变监测方面,还可以推广应用到地质研究、灾害监测和其它地形测量工程领域,为地质灾害的监测和地形形变测绘等工作提供有用的参考信息.
致谢感谢欧洲航空局提供的Envsat卫星ASAR数据和德国宇航局提供的TerraSAR-X数据,感谢香港理工大学土地测量与地理资讯学系蒋弥博士和匿名审稿专家对本文提出的意见和给予的帮助.
| [1] | 郭华东. 雷达对地观测理论与应用. 北京: 科学出版社, 2000 . Guo H D. Theory and Application of Radar Earth Observation (in Chinese). Beijing: Science Press, 2000 . |
| [2] | 王超, 张红, 刘智. 星载合成孔径雷达干涉测量. 北京: 科学出版社, 2002 . Wang C, Zhang H, Liu Z. Spaceborne Synthetic Aperture Radar Interferometry (in Chinese). Beijing: Science Press, 2002 . |
| [3] | 廖明生, 林珲. 雷达干涉测量学:原理与信号处理基础. 北京: 测绘出版社, 2003 . Liao M S, Lin H. Synthetic Aperture Radar Interferometry-Principle and Signal Processing (in Chinese). Beijing: The Publishing House of Surveying and Mapping, 2003 . |
| [4] | Massonnet D, Rossi M, Carmona C, et al. The displacement field of the Landers earthquake mapped by radar interferometry. Nature , 1993, 364(6433): 138-142. DOI:10.1038/364138a0 |
| [5] | Peltzer G, Rosen P A. Surface displacement of the 17 May 1993 Eureka valley, California, earthquake observed by SAR interferometry. Science , 1995, 268(5215): 1333-1336. DOI:10.1126/science.268.5215.1333 |
| [6] | 韩宇飞, 宋小刚, 单新建, 等. D-InSAR技术在长白山天池火山形变监测中的误差分析与应用. 地球物理学报 , 2010, 53(7): 1571–1579. Han Y F, Song X G, Shan X J, et al. Deformation monitoring of Changbaishan Tianchi volcano using D-InSAR technique and error analysis. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1571-1579. |
| [7] | 陈强, 丁晓利, 刘国祥. 永久散射体雷达差分干涉应用于区域地表沉降探测. 地球物理学报 , 2007, 50(3): 737–743. Chen Q, Ding X L, Liu G X. Radar differential interferometry based on permanent scatterers and its application to detecting regional ground subsidence. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 737-743. DOI:10.1002/cjg2.1088 |
| [8] | Oveisgharan S, Zebker H A. Estimating snow accumulation from InSAR correlation observations. IEEE Trans. Geosci. Remote Sens , 2007, 45(1): 10-20. DOI:10.1109/TGRS.2006.886196 |
| [9] | Zebker H A, Villasenor J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. , 1992, 30(5): 950-959. DOI:10.1109/36.175330 |
| [10] | Hanssen R H. Radar Interferometry:Data Interpretation and Error Analysis. Netherlands: Kluwer Academic Publishers, 2001 . |
| [11] | Rosen P A, Hensley S, Joughin I R, et al. Synthetic aperture radar interferometry. Proceedings of the IEEE , 2000, 88(3): 333-382. DOI:10.1109/5.838084 |
| [12] | Massonnet D, Feigl K. Radar interferometry and its application to changes in the Earth's surface. Review of Geophysics , 1998, 36(4): 441-500. DOI:10.1029/97RG03139 |
| [13] | Garestier F, Dubois-Fernandez P C, Champion I. Forest height inversion using high-resolution P-band Pol-InSAR data. IEEE Trans. Geosci. Remote Sens. , 2008, 46(11): 3544-3599. DOI:10.1109/TGRS.2008.922032 |
| [14] | Langley K, Hamran S E, Hogda K A, et al. Use of C-band ground penetrating radar to determine backscatter sources within glaciers. IEEE Trans. Geosci. Remote Sens. , 2007, 45(5): 1236-1246. DOI:10.1109/TGRS.2007.892600 |
| [15] | Gatelli F, Guamieri A M, Parizzi F, et al. The wavenumber shift in SAR interferometry. IEEE Trans. Geosci. Remote Sens. , 1994, 32(4): 855-865. DOI:10.1109/36.298013 |
| [16] | Lee H, Liu J G. Analysis of topographic decorrelation in SAR interferometry using ratio coherence imagery. IEEE Trans. Geosci. Remote Sens. , 2001, 39(2): 223-232. DOI:10.1109/36.905230 |
| [17] | Wang T, Liao M S, Perissin D. InSAR coherence-decomposition analysis. IEEE Geosci. Remote Sens. Lett. , 2010, 7(1): 156-160. DOI:10.1109/LGRS.2009.2029126 |
| [18] | Ferretti A, Monti-Guarnieri A, Prati C, et al. InSAR Principles:Guidelines for SAR Interferometry Processing and Interpretation. ESA Publications , 2007: A11-A12. |
| [19] | Askne J, Santoro M, Smith G, et al. Multitemporal repeat-pass SAR interferometry of boreal forests. IEEE Trans. Geosci. Remote Sens. , 2003, 41(7): 1540-1550. DOI:10.1109/TGRS.2003.813397 |
| [20] | 张红, 王超, 吴涛. 基于相干目标的DInSAR方法研究. 北京: 科学出版社, 2010 . Zhang H, Wang C, Wu T. Research of Coherent Target Differential Interferometry (in Chinese). Beijing: Science Press, 2010 . |
| [21] | Jiang M, Li Z W, Ding X L, et al. Modeling minimum and maximum detectable deformation gradients of interferometric SAR measurements. International Journal of Applied Earth Observation and Geoinformation , 2011, 13(5): 766-777. DOI:10.1016/j.jag.2011.05.007 |
| [22] | Baran I, Stewart M, Claessens S. A new functional model for determining minimum and maximum detectable deformation gradient resolved by satellite radar interferometry. IEEE Trans. Geosci. Remote Sens. , 2005, 43(4): 675-682. DOI:10.1109/TGRS.2004.843187 |
| [23] | 蒋弥, 李志伟, 丁晓利, 等. InSAR可检测的最大最小变形梯度的函数模型研究. 地球物理学报 , 2009, 52(7): 1715–1724. Jiang M, Li Z W, Ding X L, et al. A study on the maximum and minimum detectable deformation gradients resolved by InSAR. Chinese J. Geophys. (in Chinese) , 2009, 52(7): 1715-1724. |
| [24] | Askne J, Dammert P B G, Ulander L M H, et al. C-band repeat-pass interferometric SAR observations of the forest. IEEE Trans. Geosci. Remote Sens. , 1997, 35(1): 25-35. DOI:10.1109/36.551931 |
| [25] | Liao M S, Tang J, Wang T, et al. Landslide monitoring with high-resolution SAR data in the Three Gorges region. Science China Earth Sciences , 2011, 54(1): 1-12. DOI:10.1007/s11430-010-4125-6 |
| [26] | Vasile G, Trouve E, Ciuc M, et al. General adaptive-neighborhood technique for improving synthetic aperture radar interferometric coherence estimation. Journal of the Optical Society of America A , 2004, 21(8): 1455-1464. DOI:10.1364/JOSAA.21.001455 |
| [27] | Touzi R, Lopes A, Bruniquel J, et al. Coherence estimation for SAR imagery. IEEE Trans. Geosci. Remote Sens. , 1999, 37(1): 135-149. DOI:10.1109/36.739146 |
 2013, Vol. 56
2013, Vol. 56