2. 武汉大学中国南极测绘研究中心, 武汉 430079;
3. 中国测绘科学研究院, 北京 100830
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan 430079, China;
3. Chinese Academy of Surveying and Mapping, Beijing 100830, China
就类地行星及天然卫星而言,由于没有地震数据或地震数据有限,通过重力和地形数据对其内部结构进行研究是比较重要的手段之一[1-2].如果重力与地形在频率域内线性相关,那么可以使用重力和地形的导纳函数来反演地球物理参数[3].重力与地形的导纳函数,即重力与地形在频率域内的比值.利用月球重力与地形的导纳谱及相关谱,可以确定月球岩石圈的厚度[4],研究月球的均衡补偿类型,解释质量瘤的形成机制[5],进而为月球热演化提供约束[6].Crosby等于2005年利用LP视线加速度数据和Clementme任务的地形数据,使用导纳法计算了近月面古月壳的弹性厚度[7].李斐等于2009年利用月球重力场模型LP100K和地形模型GLTM2C,使用导纳方法估计了近月面主要月海区域的月壳厚度8.;^!^^等于2009年利用重力场SGM100g和地形模型STM-359,通过分析局部相关谱在不同频谱带宽和不同阶次的全球分布,比较了南极艾肯盆地(SPA)与远月面高地(FHT)弹性厚度的差别[9].Namiki于2010年利用重力场模型SGM100g与地形模型STM-359,通过分析Freundlich-Sharonov盆地的局部导纳谱与局部相关谱,研究了Freundlich-Sharonov盆地的均衡状态[10].上述研究所用模型不同,精度不一,在结果分析和精度评价上存在不足,为使研究更合理,应使用新近重力和地形模型.目前国际上较新的地形模型有美国LOLA生产的720阶次地形模型[11]、日本350阶次的STM-359[12]、中国360阶次的CLTMs01[13]等.新近地形模型的展开阶次明显高于最新重力场模型,针对同一重力场模型,不同地形模型参与导纳和相关性计算时产生的差别微小,在计算中我们选择我国嫦娥地形模型CLTMs01.本文主要研究三个高阶重力场模型LP150Q、GLGM-3、SGM150j与同一地形模型CLTMs01的导纳谱和相关谱,对比与分析它们之间的差异,为选择合适的重力场模型作导纳与相关性分析提供参考,进而使月球地球物理参数的估计更可靠.
2 基本理论 2.1 重力/地形的全球导纳函数及相关函数单位球上的任意二维可积函数可以表示成不同阶次球谐函数的线性组合[14],即有如下关系:
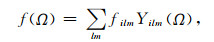
|
(1) |
其中:
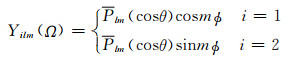
|
(2) |
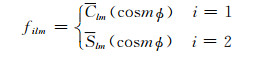
|
(3) |
其中Yilm(Ω)为l阶m次球谐函数;Plm(cosθ)为正规化的连带勒让德函数;film为相应的球谐展开系数; θ表示月球赤道坐标系中的余纬度;Ø表示月球赤道坐标系中经度.为方便表示,以下均将film和Yilm简化为Ylm和Ylm(Ω).根据球谐函数的正交性,由(1)式可得:
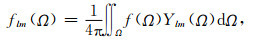
|
(4) |
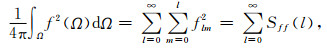
|
(5) |
其中Sff(l)为函数f(Ω)的功率谱.两球面函数f和g的交叉功率谱有如下形式:
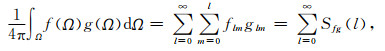
|
(6) |
若f和g分别表示球面上的地形场和重力场,可以得到地形场f和重力场g的导纳函数和相关函数:
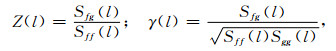
|
(7) |
其中,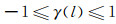

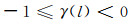
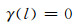
对于单位球面上的轴对称窗口函数h(θ),可将其展开为最大阶数为Lh的球谐函数的形式:
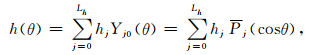
|
(8) |
可得函数f的局部函数:
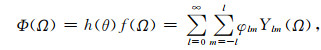
|
(9) |
其中,φlm为局部函数Φ(Ω)的l阶m次球谐展开系数.若SΦΦ(l)和SΓΓ(l)分别为函数f和函数g的局部函数的功率谱,S ΦΓ(l)为局部交叉功率谱,可得函数f和g的局部导纳和局部相关函数[15]:
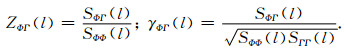
|
(10) |
本文所用重力场模型LP150Q的最大展开阶次为150阶次,在近月面的有效阶次为110阶次,远月面为60阶次,超过110阶次的位系数是利用LP任务100 km的轨道数据和拓展任务阶段40 km和30 km的轨道数据解算的,该模型可以分辨出远月面低纬度地区几个大尺度重力异常区域[16-18]. Mazarico等于2010年利用与LP150Q模型同样的数据源,按照不同的加权方法解算了150阶次的重力场模型GLGM-3.该模型与LP150Q在近月面符合得较好,而对于100阶以上的高阶信号,GLGM-3在近月面及极区与地形的相关性更强[19].美国Goddard航天中心Gossens Sander博士综合早期历史跟踪数据和SELENE数据解算了新的月球重力场模型SGM150j[20].该模型降低了低阶位系数的误差,进而提升了绕月卫星的定轨能力.为了进一步提取LP拓展任务阶段近月面短波长重力信号,避免Kaula准则引起解的有偏性,HanShin-Chan利用局部球谐函数,以GLGM-3为先验模型,成功地解算了200阶次的高阶重力场模型LPE200[21],该模型在近月面的有效阶次可达200阶.鄢建国等于2010年利用嫦娥一号探月卫星跟踪数据,结合SELENE、LP及其它历史跟踪数据,解算了新的月球重力场模型CEGM02, 该模型中低阶位系数的精度高于以往任何模型[22-23]. Hirt等于2011年利用SELENE重力场模型SGM100i和LOLA测高数据,运用“牛顿正演方法”研制了新的月球重力场模型LGM2011[24].由于CEGM02仅对低阶位系数具有明显的改进,LPE200在近月面与远月面交接处存在频谱泄露,LGM2011模型的高阶重力异常还有待GRALL任务的验证.为了方便比较,本文选择重力场模型LP150Q、GLGM-3、SGM150j参与导纳分析.根据我们的分析,L R O任务求解的地形模型、嫦娥地形模型CL丁M-s01、SELENE地形模型S丁M-359在前150阶次与同一重力场模型的导纳谱和相关谱基本没有差别,因此,本文选择地形模型CLTM-s01.
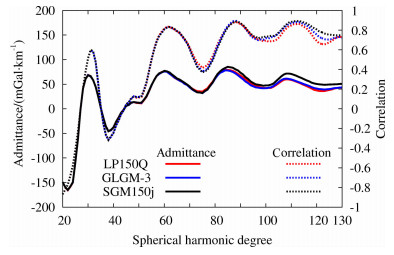
3.1 不同重力场模型的重力/地形全球导纳谱及相关谱图 1表示重力场模型LP150Q、GLGM-3、SGM150j与地形模型CLTM-sOl的全球导纳谱和全球相关谱.图 1表明LP150Q和GLGM-3在10阶次和20阶次均出现负相关值,而SGM150]仅在10阶次出现负相关值.一般认为10阶次负相关值与近月面质量瘤盆地有关,Namiki认为LP150Q在20阶次的负相关值是由于远月面重力场信息缺乏所致[25].三个模型的相关谱与导纳谱在15阶以前符合得比较好,20阶至90阶之间,SGM150]的相关值高于0.75, 明显高于LP150Q和GLGM-3, 大约在100阶以后,三个模型的导纳值及相关值相差不大.其中LP150Q与GLGM-3的导纳值和相关值在35阶以前符合得较好.而在35阶至80阶之间,LP150Q的导纳值和相关值比GLGM-3的高.而在80阶至150阶之间,LP150Q与GLGM-3的导纳值和相关值相差不大.这是由于LP150Q和GLGM-3使用了相同的数据源,但数据处理方法不同所致.在100阶至150阶之间,SGM150]的导纳值仍然比其它模型的高.这是由于LP150Q和GLGM-3仅在近月面有卫星轨道的观测值,远月面存在严重的数据缺失,而SELENE任务使用卫星跟踪卫星的方式,在远月面也有卫星跟踪数据的观测量.远月面观测数据的补充增强了SGM150]的全球功率谱,使得SGM150]的导纳值和相关值甚至在100阶至150阶之间也高于其它模型,这说明远月面重力场信息的补充有助于增强重力场模型在中高频段的导纳值和相关值.
|
图 1 不同重力场模型的导纳谱(实线)和相关谱(虚线) Fig. 1 Gravitational admittance(solid lines)and Correlation(dashed lines) spectra of different gravity model |
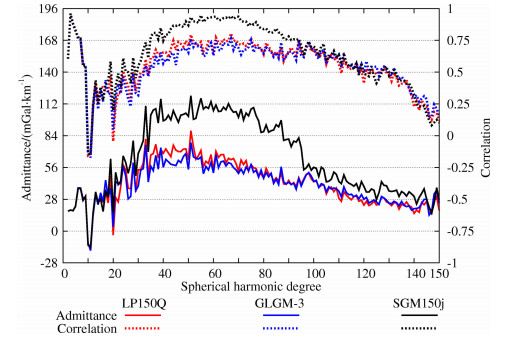
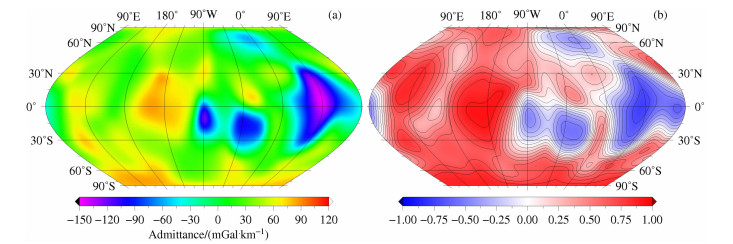
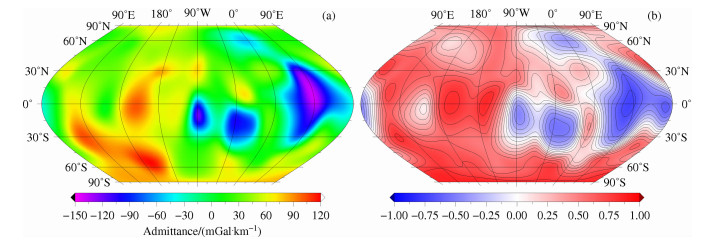
本文采用“空间-频谱”(spatio-spectral)方法[26],选择半径为常数的固定窗口Lwin,计算了重力/地形局部导纳谱与局部相关谱的全球分布.计算过程选择频谱带宽Lwin=5阶的窗口,对应的空间尺度D约为2200 km,该尺度能够分辨出月球表面大范围的特征.图 2-4分别表示基于重力场模型LP150Q、GLGM-3、SGM150:j,窗口带宽Lwin=5,l=20阶的局部导纳谱与局部相关谱的全球分布,所有图形均使用赫墨尔等面积投影方式(Hammer equal-area projections), 投影中心为(0°N, 90°W), 左边为远月面,右边为近月面.图 2-4均表明近月面的危海、宁静海、丰富海、史密斯海和酒海等整个大片区域处于负相关状态,相应的导纳值也为负.这是由于这部分区域分布着许多大型质量瘤盆地,重力异常值在400 mGal左右,而高程值却在-4~-2 km之间,如此大的重力异常值对应的高程值却为负,因此在这部分区域出现了负相关.在湿海和东方海附近也出现了负相关,相应的重力导纳值也为负.这部分区域的重力异常值大约在200〜400 mGal之间,高程值在-3 km左右,因此重力与地形表现为负相关.三个模型在近月面的局部导纳谱与局部相关谱的分布相同,这说明三个重力场模型对低阶重力场信号的敏感程度相同,均适合作近月面长波长重力/地形导纳谱与相关谱的研究.图 2表明LP150Q在赤道附近,经度-145°的区域为正相关,这部分区域在图 3中则表现为分离的两个正相关区域.GLGM-3在远月面零相关区域的数量总体上较LP150Q多,相关性较LP150Q弱,这是由于GLGM-3对远月面重力场的敏感度低于LP150Q所致.图 4表明SGM150]在远月面除史密斯海边缘区为负相关,少部分区域接近零相关外,其余大部分区域为正相关.这是由于SELENE任务采用中低卫星跟踪方式,在远月面有大量的观测数据,因此SGM150]在远月面的分辨率高于LP150Q和GLGM-3, 对远月面高阶重力场的敏感度也高于其它模型.SGM150在远月面大部分区域相关性较强,这说明SGM150]对远月面重力/地形局部导纳谱与局部相关谱的分析较适合.
|
图 2 基于LP150Q,窗口为5阶时,局部导纳值与相关值在L=20阶时的全球分布 Fig. 2 Global admittance (left column) and correlation (right column) maps localized at harmonic degree 20 with window of spectral width Lwin=5 for gravity field model LP150Q |
|
图 3 基于GLGM 3,窗口为5阶时,局部导纳值与相关值在L=20阶时的全球分布 Fig. 3 Global admittance (left column) and correlation (right column) maps localized at harmonic degree 20 with window of spectral width Lwin=5 for gravity field model GLGM 3 |
|
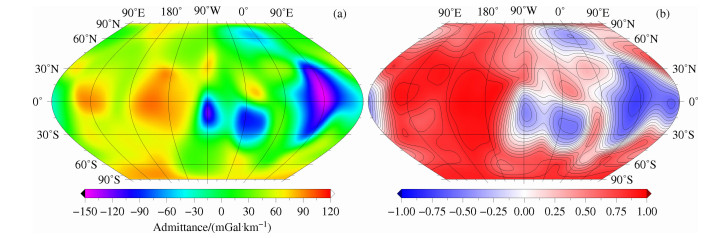
图 4 基于SGM150j,窗口为5阶时,局部导纳值与相关值在L=20阶时的全球分布 Fig. 4 Global admittance (left column) and correlation (right column) maps localized at harmonic degree 20 with window of spectral width Lwin=5 for gravity field model SGM150j |
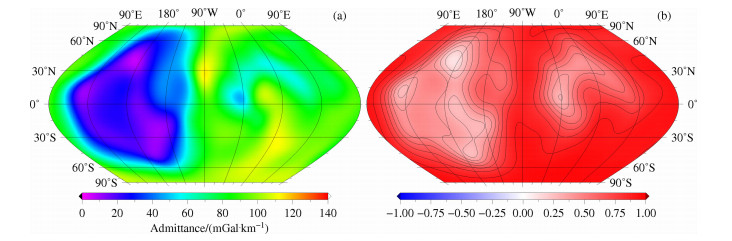
图 5-7分别表示基于重力场模型LP150Q、GLGM-3、SGM150:j,窗口带宽Lwin=5时,在l=65阶次的局部导纳谱与局部相关谱的全球分布,所有图形均使用赫墨尔等面积投影方式(Hammer equal-area projections), 投影中心为(0°N, 90°W), 左边为远月面,右边为近月面.由图 5-7可知,三个模型在近月面的局部相关谱分布(图b右边)大致相同,仅在远月面存在差别.图 6表明GLGM-3在远月面大部分区域为零相关区域,相应区域的零相关性在图 5中则较弱.图 7表明SGM150]在远月面除了北纬30°西经180°的少数区域存在较弱的零相关外,其余大部分区域为正相关.由于SGM150]在远月面与地形的相关性较强,因此较适合于作远月面局部导纳谱与局部相关谱分析.另外,SGM150]在近月面部分区域(22. 5°W,10°N)的导纳谱(图a)高于其它模型.这是由于SGM150]加人了远月面真实的重力场信息,有效阶次可达70阶次,使得SGM150在近月面的中高频段的强度高于其它模型,因此图 7中近月面这部分区域(22. 5°W,10°N)出现了高导纳值.这也可以由图 1看出,在65阶附近,基于SGM150j的导纳值与相关值明显高于其它模型.对比图 4和图 7可知,图 4中近月面大部分区域为负相关,而图 7中则为正相关.这是由于图 4中20阶次的长波长信号一般来自质量瘤盆地,而65阶次短波长信号一般来自未补偿的地形.未补偿地形产生的重力异常,其功率谱与未补偿地形的功率谱应有相同的分布,因此图 7中近月面大部分区域为正相关.
|
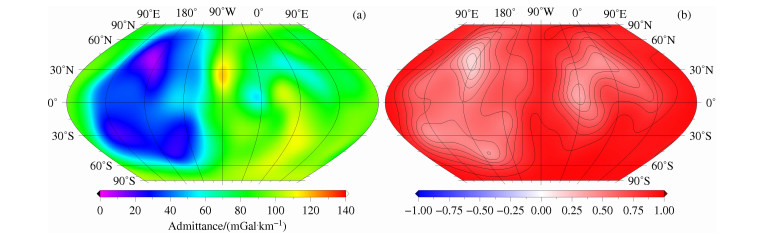
图 5 基于LP150Q,窗口为5阶时,局部导纳值与相关值在L=65阶时的全球分布 Fig. 5 Global admittance (left column) and correlation (right column) maps localized at harmonic degree 65 with window of spectral width Lwin=5 for gravity field model LP150Q |
|
图 6 基于GLGM 3,窗口为5阶时,局部导纳值与相关值在L=65阶时的全球分布 Fig. 6 Global admittance (left column) and correlation (right column) maps localized at harmonic degree 65 with window of spectral width Lwin=5 for gravity field model GLGM 3 |

|
图 7 基于SGM150j,窗口为5阶时,局部导纳值与相关值在L=65阶时的全球分布 Fig. 7 Global admittance (left column) and correlation (right column) maps localized at harmonic degree 65 with window of spectral width Lwin=5 for gravity field model SGM150j |
图 8表示近月面危海区域局部导纳谱与局部相关谱的分布.图 8表明三个重力场模型的局部导纳谱与局部相关谱的总体分布相同,在80阶后的高阶项出现较小的差别.三个模型均在20阶处出现负导纳值和负相关值,导纳值大约为-16 0 mGal/km, 相关值约为-0. 8, 这说明这部分区域存在明显的剩余质量(质量瘤).由于质量瘤的存在,较高的正重力异常与较低的地形形成了明显的负相关.LP、Clementine和SELENE卫星在正常任务阶段(平均轨道高度约为100 km),他们在近月面的观测精度相同.而在高阶次处,由于各自综合的历史数据及处理方式的不同,因此局部导纳谱与局部相关谱在高阶次处出现较小的差别.由此可知,三个模型均适合于作危海区域局部导纳谱与局部相关谱的分析,适合于作该区域地球物理参数的估计.
|
图 8 危海在不同重力场模型下的局部导纳谱(实线)和局部相关谱(点线) Fig. 8 Localized admittance (solid line) and correlation (dot line) spectra in Mare Crisim for different gravity field model |
图 9表示莫斯科海区域的局部导纳谱与局部相关谱.由图 9可知,在20阶至30阶之间,三个模型的相关谱单调减小.基于SGM150j的相关值在37阶左右减小到-0.9, 相应的导纳值大约为一280 mGal/km,其它模型的相关值大约在一0. 6左右,相应的导纳值大约为一150 mGal/km.SGM150j的相关性高于其它模型,这说明SGM150j能够提供较可靠的质量瘤信息,适合于作局部导纳分析.大约在41阶以后,三个模型的相关值和导纳值单调增加.大约在45阶至58阶之间,SGM150j的相关值增大到0. 8以上,而其它模型的相关值大约在0. 6左右.而70至90阶之间,基于SGM150j的相关值在0. 5以上,而基于LP150Q和GLGM-3的相关值在0.4以下.由上可知,SGM150j与地形的相关性强于其余模型,适合于作远月面局部导纳谱与相关谱分析,较适合于作远月面局部区域地球物理参数的估计.
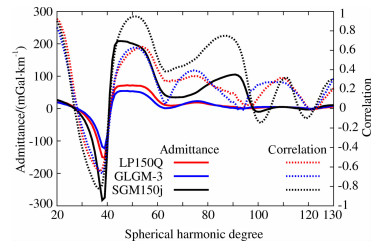
|
图 9 莫斯科海在不同重力场模型下的局部导纳谱(实线)和局部相关谱(点线) Fig. 9 Local admittance (solid line) and correlation (dot line) spectra in Mare Moscoviense for different gravity field model |
图 10表示门捷列夫(Mendeleev)撞击坑基于不同重力场模型的局部导纳谱与局部相关谱.图 10表明在27阶至40阶之间,SGM150j的相关值接近于1,相应的导纳值高于其它模型.在55阶至75阶之间,SGM150j的相关值接近1,相应的导纳值在140 mGal/km以上,明显高于其它模型,这说明SGM150j适合于作远月面撞击坑中高阶次的局部导纳分析,适合于作相应区域地球物理参数的估计.另外,图 10中SGM150j的相关值在高阶项83阶处为负相关,这说明门捷列夫(Mendeleev)撞击坑异常质量的尺度较小,分布较浅.图 8表明三个重力场模型的导纳谱和相关谱的差异较小,而图 9和图 10表明三个模型的局部导纳谱和局部相关谱的差异较大,这是由于三个重力场模型在近月面的有效阶次相近,而在远月面存在较大的差异所致.对比图 8和图 9, 危海区域的最小负相关值出现在20阶左右,而莫斯科海区域的最小负相关值出现在40阶左右,这说明危海区域异常质量的尺度比莫斯科海区域的大,分布也比莫斯科海区域的深.梁青等认为,远月面高地型质量瘤盆地,形成于前酒海纪至酒海纪.异常质量由填充的高密度玄武岩组成,主要分布在盆地的浅层区域;而诸如危海一类的平原型质量瘤盆地,形成时间晚于高地类质量瘤盆地,异常质量主要分布在盆地的深部区域,为上隆的月幔物质组成[27].本文所得结论与他们的相同,即近月面质量瘤盆地异常质量的深度和尺度高于远月面的情况.
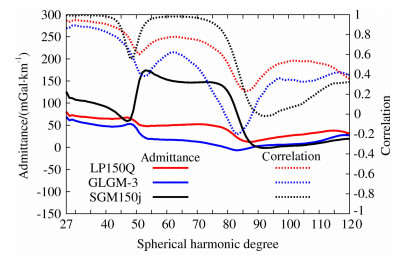
|
图 10 门捷列夫坑在不同重力场模型下的局部导纳谱(实线)和局部相关谱(点线) Fig. 10 Local admittance (solid line) and correlation (dot line) spectra in Crater Mendeleev for different gravity field model |
本文以嫦娥地形模型CLTM-s01为基准,使用重力/地形的全球和局部导纳谱与相关谱对比与分析了三个高阶重力场模型LP150Q、GLGM-3和SGM150j的差异,结果表明:
(1) SGM150j的全球导纳谱与全球相关谱在20阶至90阶之间高于LP150Q和GLGM-3.这说明加入远月面重力场信息有助于增强重力场模型在中高频段的信号强度,即增强重力场模型中高频段的功率谱.LP150Q、GLGM-3、SGM150j的局部导纳谱与局部相关谱在近月面的分布基本一致.三个模型均适合于作近月面局部导纳谱与局部相关谱分析,适合于作近月面地球物理参数的估计.
(2) 三个模型的局部导纳谱与局部相关谱在远月面存在较大的差异,随着球谐阶次的增加,差异逐渐增大, 因此,LP150Q和GLGM-3较适合于作远月面大范围的研究,不适合于作远月面的局部导纳谱与局部相关谱分析,不适合于作远月面局部区域地球物理参数的估计.作远月面局部区域地球物理参数的估计,SGM150:j较适合.
(3) 根据近月面典型质量瘤盆地局部负相关谱与远月面质量瘤盆地的差别,近月面大型质量瘤盆地异常质量的尺度比远月面质量瘤盆地的大,深度也比远月面的深.
致谢本文所用的重力场球谐系数取自美国NASA PDSGeoscience Node Data中心和日本JAXASELENE DataArchive中心,球谐分析使用了SHTOOLS2.5, 球面投影采用了TheGeneric Mapping Tools(GMT)软件.感谢审稿专家提出的宝贵意见.
| [1] | Kaula W M. An Introduction to Planetary Physics:The Terrestrial Planets. New York: John Wiley, 1968 . |
| [2] | McKenzie D. Surface deformation, gravity anomalies, and convection. J. Geophysics. Res. , 1977, 48(2): 211-238. |
| [3] | Turcotte D L, Willemann R J, Haxby W F, et al. Role of membrane stresses in the support of planetary topography. J. Geophysics. Res. , 1981, 86(B5): 3951-3959. DOI:10.1029/JB086iB05p03951 |
| [4] | Lewis B T R, Dorman L M. Experimental Isostasy:2. An isostatic model for the U.S.A. derived from gravity and topographic data. J. Geophys. Res. , 1970, 75(17): 3367-3386. DOI:10.1029/JB075i017p03367 |
| [5] | Willemann R J, Turcotte D L. Support of topographic and other loads on the moon and on the terrestrial planets. Proc. Lunar Planet Sci. , 1981, 12B: 837-851. |
| [6] | Parsons B, Sclater J G. An analysis of the variation of ocean floor bathymetry and heat flow with age. J. Geophys. Res. , 1977, 82(5): 802-827. |
| [7] | Crosby A, McKenzie D. Measurements of the elastic thickness under ancient lunar terrain. Icarus , 2005, 173(1): 100-107. DOI:10.1016/j.icarus.2004.07.017 |
| [8] | 李斐, 柯宝贵, 王文睿, 等. 利用重力地形导纳估计月壳厚度. 地球物理学报 , 2009, 52(8): 2001–2007. Li F, Ke B G, Wang W R, et al. Estimation of the ancient lunar crust thickness from the admittance. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2001-2007. |
| [9] | Ishihara Y, Namiki N, Sugita S, et al. Localized Gravity/Topography Correlation and Admittance Spectra on the Moon. Lunar and Planetary Science Conference , 2009, 40th: 1623. |
| [10] | Namiki N. Admittance and Correlation of Localized Gravity and Topography of Freundlich-Sharonov Basin of the Moon. Lunar and Planetary Science Conference , 2010, 41st: 1885. |
| [11] | Smith D E, Zuber M T, Neumann G A, et al. Initial observations from the Lunar Orbiter Laser Altimeter(LOLA). Geophys. Res. Lett. , 2010, 37(18): 1-6. |
| [12] | Araki H, Tazawa H, Noda H, et al. Lunar global shape and polar topography derived from Kaguya-LALT laser altimetry. Science , 2009, 323(5916): 897-900. DOI:10.1126/science.1164146 |
| [13] | 平劲松, 黄倩, 鄢建国, 等. 基于嫦娥一号卫星激光测高观测的月球地形模型CLTM-s01. 中国科学G辑 , 2008, 38(11): 1601–1612. Ping J S, Huang Q, Yan J G, et al. Lunar topographic model CLTM-s01 from Chang'E-1 laser altimeter. Science in China Series G (in Chinese) , 2008, 38(11): 1601-1612. |
| [14] | Heiskanen W A, Moritz H. Physical Geodesy. San Francisco: Freeman, 1967 . |
| [15] | Wieczorek M A, Simons F J. Localized spectral analysis on the sphere. J. Geophys. Res. , 2005, 162(3): 655-675. |
| [16] | Konopliv A S. The lunar prospector Garvity Science Team, LP150Q Spherical Harmonic Model, 2000, available at http://pds-geosciences.wustl.edu/lunar01/lp-l-rss-5-gravity-v1/lp1001/sha/jg1150q1.sha2 |
| [17] | Konopliv A S, Asmar S W, Carranza E, et al. Recent gravity models as a result of the lunar prospector mission. Icarus , 2001, 150(1): 1-18. DOI:10.1006/icar.2000.6573 |
| [18] | 鄢建国, 平劲松, 李斐, 等. 应用LP165P模型分析月球重力场特征及其对绕月卫星轨道的影响. 地球物理学报 , 2006, 49(2): 408–414. Yan J G, Ping J S, Li F, et al. Character analysis of the lunar gravity field by the LP165P model and its effect on lunar satellite orbit. Chinese J. Geophys. (in Chinese) , 2006, 49(2): 408-414. |
| [19] | Mazarico E, Lemoine F G, Han S H, et al. GLGM-3:A degree-150 lunar gravity model from the historical tracking data of NASA Moon orbiters. J. Geophysics. Res. , 2010, 115(E05001): 1-14. |
| [20] | Goossens S J, Matsumoto K, Kikuchi F, et al. Improved high-resolution lunar gravity field model from SELENE and historical tracking data. AGU Fall Meeting, Abstract p44B-05, 2011. |
| [21] | Han S C, Mazarico E, Rowlands D, et al. New analysis of Lunar Prospector radio tracking data brings the nearside gravity field of the moon with an unprecedented resolution. Icarus , 2011, 215(2): 455-459. DOI:10.1016/j.icarus.2011.07.020 |
| [22] | 鄢建国, 平劲松, MatsumotoK, 等. 嫦娥一号绕月卫星对月球重力场模型的优化. 中国科学:物理学力学天文学 , 2011, 41(7): 870–878. Yan J G, Ping J S, Matsumoto K, et al. Optimization on lunar gravity field model using Chang'E-1 orbital tracking data. Scientia Sinica Phy, Mech & Astron (in Chinese) , 2011, 41(7): 870-878. |
| [23] | Yan J G, Goossens S, Matsumoto K, et al. CEGM02:An improved lunar gravity model using Chang'E-1 orbital tracking data. Planetary and Space Science , 2011, 62(1): 1-9. DOI:10.1016/j.pss.2011.11.010 |
| [24] | Hirt C, Featherstone W E. A 1.5 km-resolution gravity field model of the moon. Earth and Planetary Science Letters , 2012, 329-330: 22-30. DOI:10.1016/j.epsl.2012.02.012 |
| [25] | Namiki N, Iwata T, Matsumoto K, et al. Farside gravity field of the Moon from four-way Doppler measurements of SELENE(Kaguya). Science , 2009, 323(5916): 900-905. DOI:10.1126/science.1168029 |
| [26] | Simons M, Simons S C, Simons B H. Localization of gravity and topography:constraints on the tectonics and mantle dynamics of Venus. J. Geophysics. Res. , 1997, 131(1): 24-44. |
| [27] | 梁青, 陈超, 黄倩, 等. 基于嫦娥一号地形数据的月球布格重力异常与撞击盆地演化. 中国科学G辑 , 2009, 39(10): 1379–1386. Liang Q, Chen C, Huang Q, et al. Bouguer gravity anomaly of the Moon from CE-1 topography data:Implications for the impact basin evolution. Science in China Series G (in Chinese) , 2009, 39(10): 1379-1386. |
 2013, Vol. 56
2013, Vol. 56


