2. 吉林大学物理学院, 长春 130012
2. College of Physics, Jilin University, Changchun 130012, China
据估计,世界上大约有30%的油气储存于砂-泥岩薄交互层中[1],这种薄交互储层可等效为宏观的单轴各向异性地层[2](或称横向各向同性地层,简记为TI地层),探测和识别这类地层对于油气资源的开发有重要意义和现实需要.现有的轴向型感应测井仪器由于纵向分辨率还不够高,往往将这种薄交互油储层误认为是高含水饱和度层而漏掉[3].三维感应测井仪器是由三个彼此垂直的发射线圈和与之平行的三个接收线圈组成,能探测到地层的水平电导率和垂直电导率信息,可以从三维角度识别地层特性,对薄储层、复杂储层的探测具有先天的优势.快速正演模拟是研究测井响应特征和资料处理的必要计算工具.含井眼和纵向邻层的非均质地层中三维感应测井响应的求解是三维问题,没有正演解析解,只能用有限元和有限差分等数值计算方法求解[4-7],其计算工作量大,计算时间长.忽略井眼环境的水平层状地层模型可用来研究纵向邻层对测井响应的影响及经过井眼效应校正的测井资料的直观解释与非线性迭代反演.国内外已经发表了大量关于水平层状各向异性地层中三轴感应测井响应的快速算法研究,如数值模式匹配方法、传输线理论和传播矩阵法等[8-14],这些算法本质上都是计算层状各向异性介质中的电磁场,并且计算效率相当.本文针对水平和垂直线圈源(等价为磁偶极子源)激发的TE波和TM波,利用广义反射系数递推方法推导了纵向行波的递推公式,给出了水平层状各向异性介质中电磁场积分解析解的另一种表达形式,并利用快速汉克尔变换技术[15]实现其快速计算.
三维感应测井响应与地层水平电导率、垂直电导率和井斜角同时有关,且非线性严重,加上邻层对不同分量测井曲线的影响又大不一样,其资料的直观解释很难取得好的效果[16].此外,除共轴分量外其余分量都与仪器方位角有关也增加了资料解释的困难.目前,三维感应测井资料处理除多频聚焦方法(MFF)外,主要是多参数非线性迭代反演方法[9, 17],而测井资料的直观解释却鲜有报道.迭代反演方法可以获得更接近真值的地层参数,但其计算速度慢,并不能满足现场对测井资料解释的需要,属于测井资料后处理.资料直观解释计算速度快,有利于测井资料的现场处理,并可为进一步的非线性迭代反演提供好的初始值.本文数值模拟了三维感应测井仪器9个分量随测量深度和仪器方位角变化的响应曲线,并对模拟数据给出了基于组合量测井曲线的直观处理,得到了一些有意义的结果.
2 三维感应测井响应快速计算 2.1 TI介质中TE波和TM波的分解
在TI介质的主轴坐标系O-XYZ中电导率可表示为对角张量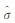
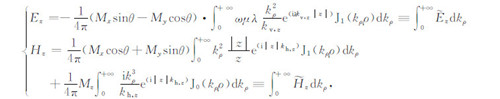
|
(1) |
其中Jn()为n阶Bessel函数,kρ为积分变量,kv,z=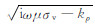
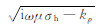
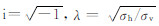
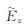
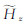
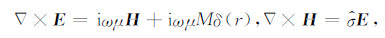
|
(2) |
得到波数域中电磁场水平分量:
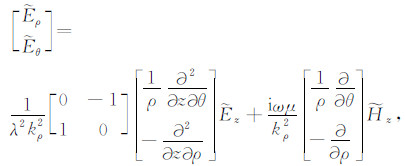
|
(3) |
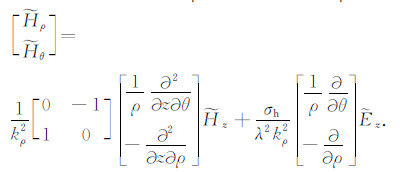
|
(4) |
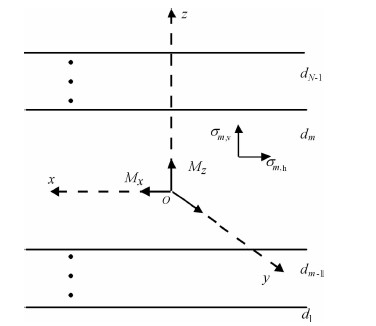
利用TE波和TM波分解技术,我们只需推导波数域中电磁场法向分量在地层中的分布,然后由式(3)和(4)即可求解电磁场的水平分量.图 1为N个水平层状各向异性地层模型,层界面位置用dn(n=1,2,…,N-1)表示;地层n的磁导率μn为各向同性;电导率用张量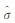
|
图 1 水平层状各向异性地层模型 Fig. 1 Model of horizontal layered anisotropy formation |
令源所在的位置为坐标原点,所在层为第m层,则任意层n的电磁场法向分量可表示为纵向行波与柱面波的叠加:
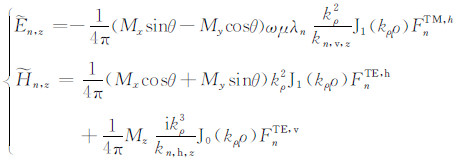
|
(5) |
F为纵向行波的传播项,上角标TM,h表示由水平磁偶极子源激发的TM波,其余类推;对不同模式波,传播项F的表达式略有不同,但可统一写为:(详细推导见附录A)
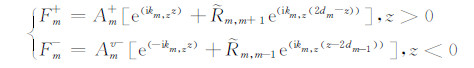
|
(6) |
其中,上角标“±”分别代表上行波和下行波;A为振幅,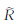
对于传播项FmTE,v,将式(6)中的指数因子做替换kz→kh,z,振幅具体展开为:
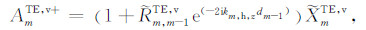
|
(7a) |
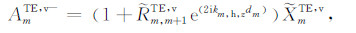
|
(7b) |
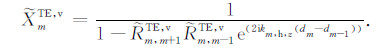
|
(7c) |
对于传播项FmTE,h,将式(6)中的指数因子做替换kz→kh,z,振幅具体展开为:
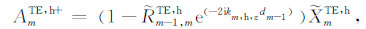
|
(8a) |

|
(8b) |

|
(8c) |
对于传播项FmTM,h,将式(6)中的指数因子做替换kz→λkv,z,振幅具体展开为:
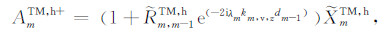
|
(9a) |
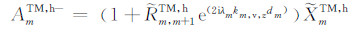
|
(9b) |
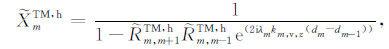
|
(9c) |
由式(5)和(6)可以看出,如果知道每一层的广义反射系数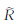

|
(10) |
上行波在m+1层中的振幅Am+1+可表示为边界z=dm处的反射波和透射波振幅的迭加:
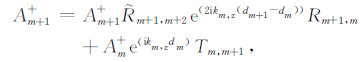
|
(11) |
其中Rm+1,m和Tm,m+1为m层对m+1层的狭义反射和透射系数,整理后
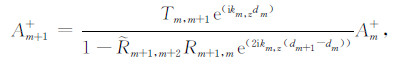
|
(12) |
同理,下行波在m-1层中的振幅Am-1-为:
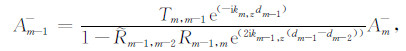
|
(13) |
重复上面的推导过程,我们得到其余相邻层振幅的递推关系:
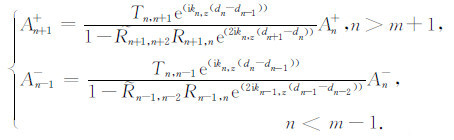
|
(14) |
各向异性地层的广义反射系数可由相邻两层的狭义反射、透射系数表示[19],利用电磁场水平分量在边界处的连续条件,由式(3)和(4)得:
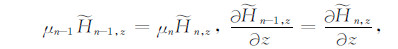
|
(15) |
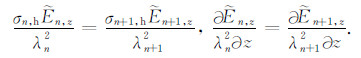
|
(16) |
由此,上述三种模式波在边界处狭义反射、透射系数的具体表达式可写为:
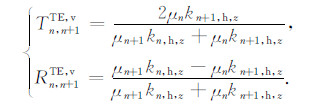
|
(17) |

|
(18) |

|
(19) |
类似于水平层状各向同性地层模型中广义反射系数的推导方式[19],可推导出水平层状各向异性地层中广义反射系数的递推公式并整理成统一的表达形式:
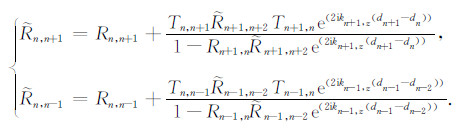
|
(20) |
为满足自然边界条件有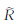
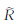
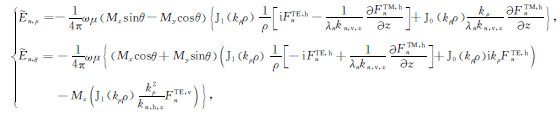
|
(21) |
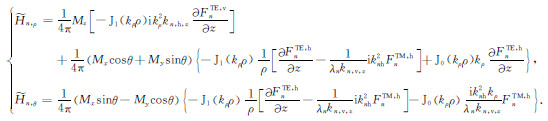
|
(22) |
由式(5)和式(22)可以看出,水平磁偶极子源激发的磁场水平分量同时与地层水平电导率和垂直电导率有关,法向分量只与水平电导率有关;垂直磁偶极子源激发的磁场法向分量和水平分量都只与水平电导率有关,与垂直电导率无关.这些基本关系将有助于三维感应测井响应特征考察与资料处理.空间域中的电磁场积分表达式为:
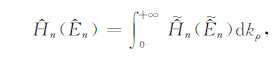
|
(23) |
式(23)的右端为Sommerfeld积分表达式,其积分核是慢衰减的高震荡函数.由于水平层状地层模型的波数域电磁场分量是解析递推,计算速度快,所以空间域中电磁场分量的计算速度主要取决于Sommerfeld积分计算效率.陈桂波等[20]详细比较了快速汉克尔变换技术、高阶窗函数结合连分式展开技术以及直接积分等方法求解Sommerfeld积分的计算效率,发现快速汉克尔变换技术的计算效率最高,是高阶窗函数结合连分式展开技术的3倍,直接积分的27倍.本文也采用这种求解方法.
2.3 三维感应测井视电导率响应分量三维感应测井仪器的线圈系结构(图 2所示)由三个中心共点的、彼此垂直的发射线圈Tx,Ty,Tz和与其平行的三个接收线圈Rx,Ry,Rz(源距为L1)三个屏蔽线圈Bx,By,Bz(源距为L2)组成.屏蔽线圈可抵消发射线圈在接收线圈中产生的直耦信号,其绕线方向与接收线圈的相反.

|
图 2 三线圈系结构示意图 Fig. 2 The diagram of three-coil system |
当发射线圈系向周围发射正弦交流电时,三维感应测井仪器同时测量接收线圈系上的九个磁场分量,它们构成完整的二阶张量:
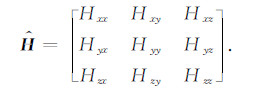
|
(24) |
为了考察倾斜井中三维感应测井响应,需引入三个坐标系:地层坐标系O-XYZ(介质主轴坐标系)、仪器坐标系O-X'Y'Z'和线圈坐标系O-X″Y″Z″[21].三个坐标系下的磁场张量满足如下旋转变换规则:
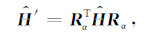
|
(25) |

|
(26) |
其中
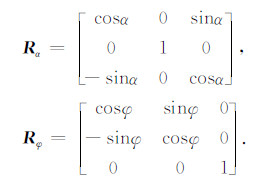
|
(27) |
α是仪器轴与地层法向分量之间的夹角,即井眼斜角;φ是仪器绕自身旋转的方位角,即仪器方位角.经补偿后,接收线圈测量的磁场强度HijA可表示为:
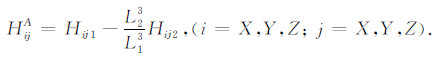
|
(28) |
为便于测井响应与地层电参数之间的比较,通常将感应测井响应规格化为电导率量纲的测量,记为σijA [22]:
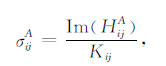
|
(29) |
其中Im(HijA)为磁场的虚部,Kij为线圈系仪器系数.
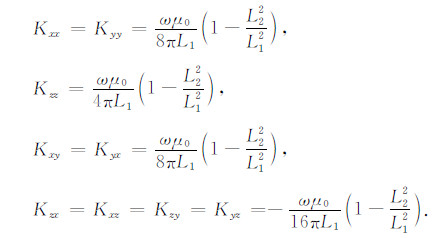
|
(30) |
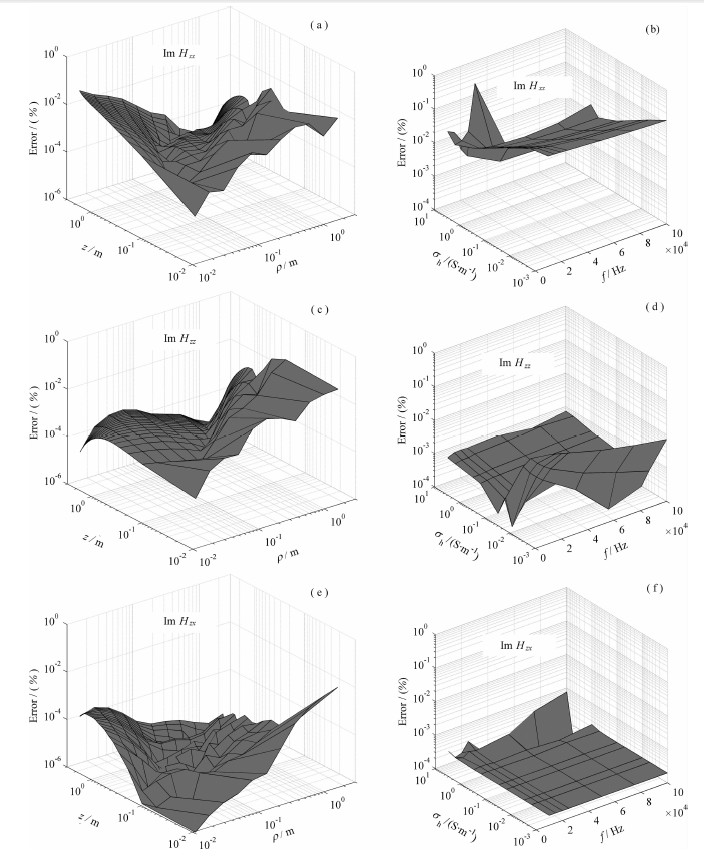
快速汉克尔变换技术计算效率高,但其计算精度容易受仪器参数及地层参数变化的影响[20].下面我们考察一般条件下感应测井快速汉克尔变换技术的计算精度.感应测井仪器接收点距离发射源点一般为0.3~2.0 m,发射源频率为10~100kHz,地层电导率变化范围0.001~10.0S/m.图 3给出了均匀各向异性介质中利用快速汉克尔变换技术计算的磁场分量虚部与其代数解析解[23]的相对误差.图 3(a、c、e)仪器发射频率f=25kHz,地层水平电导率σh=1.0s/m、σh/σv=2;(b、d、f)仪器发射点为坐标原点,接收点为(1,0,1).可以看出绝大部分相对误差都在0.1%以下,满足计算精度的要求.
|
图 3 快速汉克尔变换技术的计算精度 Fig. 3 The calculation precision of fast Hankel transform technology |
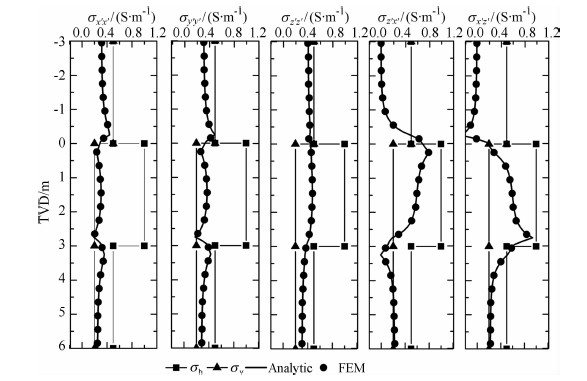
水平层状各向异性地层模型没有代数解析解,图 4给出了三层模型中本文推导的解析解(曲线)与有限元法[7](点线)模拟的三维感应测井响应结果的比较.目标层厚为3 m,地层电导率依次为:σ1,h=σ1,v=0.5S/m,σ2,h=1S/m,σ2,v=0.1S/m,σ3,h=0.5S/m和σ3,v=0.125S/m;井眼倾角α=60°,发射频率为f=25kHz,主接收线圈源距L1=39in,补偿线圈源距L2=27in,方位角φ=0°.在Pentium 2.9GHz计算机上,200个测量点计算所需总计算时间为0.55s.从图 4可以看出,两种方法的结果完全一致,证明了本文的计算方法是正确的、高效的.
|
图 4 解析解与有限元方法模拟结果的对比 Fig. 4 ComparethesimulationresultsbetweentheanalyticsolutionandtheFEM method |
由式(26)知,一般情况下倾斜井中三维感应测井响应的9个分量都不为零,且除轴向分量外,其余分量都是仪器方位角的函数.图 5给出了在同时含有各向同性层和各向异性层的地层模型中随仪器旋进的测井响应数值模拟曲线.井眼斜角α=60°,地层模型层厚22.5 m,仪器实际测量的行进距离(测量深度MD)是45m;假定沿测量深度的测量间隔是0.1m;每个测量间隔仪器方位角逆时针旋进5°;仪器参数同上.
|
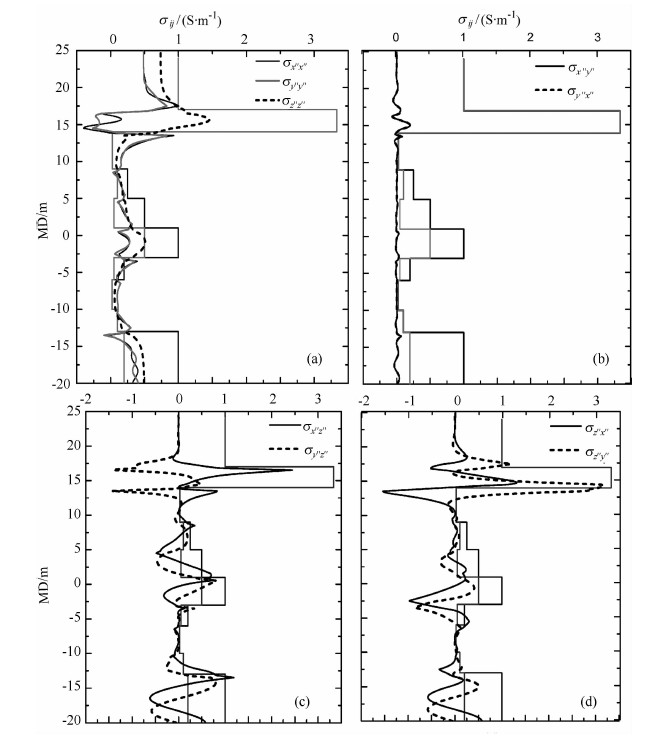
图 5 线圈坐标系下测井响应数值模拟 Fig. 5 Numerical simulation of the tool response under coil system |
由图 5a可以看出,共面分量视电导率响应σx″x″和σy″y″受邻层影响比共轴分量σz″z″的要大,在边界702附近有“犄角”特性,甚至出现负响应,这主要是由层边界的电荷积累引起的.σx″x″和σy″y″的响应行为很接近,但受各向异性电阻率或纵向邻层的影响,其测井曲线并不重合;随着仪器方位角的旋进,σx″x″和σy″y″在厚层内测井曲线会出现波动.共轴分量视电导率响应σz″z″曲线比较光滑,其响应值与地层水平电导率的走势有一致的对应关系.由式(26)可知,σz″z″响应值与仪器方位角无关.图 5b是交叉分量视电导率响应σx″y″和σy″x″,它们相互重叠并在零点附近波动.图 5c和5d是交叉分量视电导率响应σx″z″、σy″z″和σz″x″、σz″y″,它们的响应幅度波动很大,特别是在地层边界附近.
从上面的分析可以看出视电导率响应分量是地层各向异性电导率和几何角度的函数,单一的测井响应很难反映地层真实电导率的纵向分布和划分地层纵向边界.在资料处理上,现在普遍采取首先将测得的9条响应曲线变换成仪器坐标系(仪器方位角为零)中5条不为零的测井曲线再做资料解释.由于仪器方位角的变化范围是0~180°,现有的求解方法[21, 24]都不能由单一测量点确定方位角所属的象限和逐点转化仪器坐标系中的测井响应分量.本文利用线圈坐标系中直接测量的响应曲线构造出三条与仪器方位角无关的响应曲线σ-、σ+和σapp.组合曲线的构造方法如下:
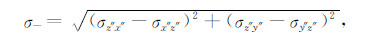
|
(31) |
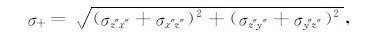
|
(32) |
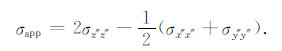
|
(33) |
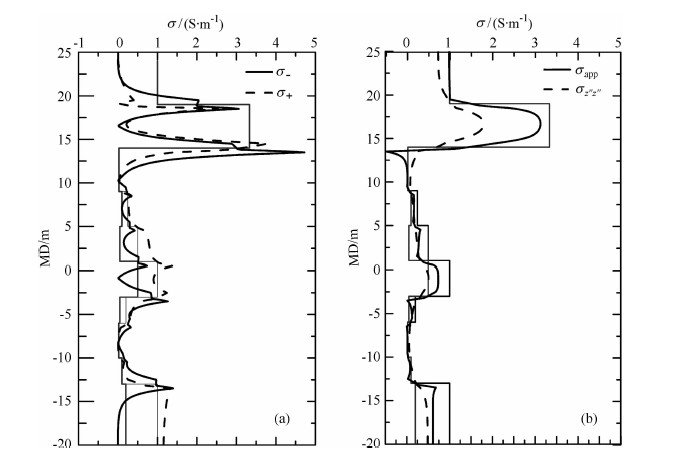
图 6给出了由图 5中测井响应曲线构造的组合曲线σ-、σ+和σapp.由图 6a可见,组合曲线σ-和σ+的形态显著地规则化了,所受邻层的影响显著减少了,与地层参数之间的关系变得简单和直观了:组合曲线σ-的峰值附近响应曲线明显的有规律的弯折是由屏蔽线圈造成的,峰值与地层边界位置相对应.σ-的测井响应与地层垂直电导率无关,峰值的大小与相邻两层水平电导率的反差成正比[25].组合曲线σ+在各向异性层中的响应值明显偏离零,在各向同性层中响应值趋近零,利用这一响应特征可直观识别各向异性地层.图 6b中组合曲线σapp比共轴分量σz″z″的纵向分辨率明显提高;各向同性地层中的响应值与其真值很接近,各向异性层中的响应值处于水平电导率和垂直电导率之间,但比σz″z″更接近地层水平电导率,这是因为组合量σapp与电导率的非线性关系比σz″z″的更弱.综合利用这三条构造组合曲线,我们给出三维感应测井初步的直观解释流程:首先利用组合曲线σ-分层和确定边界位置;其次利用组合曲线σ+区分各向异性层和各向同性层;最后利用组合曲线σapp的标志点给出各向同性地层的视电导率及各向异性层中水平电导率视值.由于各向异性垂直电导率往往比较小,探测灵敏度低,它的视值解释方法与水平电导率的也不同,还需进一步研究.
|
图 6 构造组合曲线的数值模拟 Fig. 6 The numerical simulation of the combination curves |
|
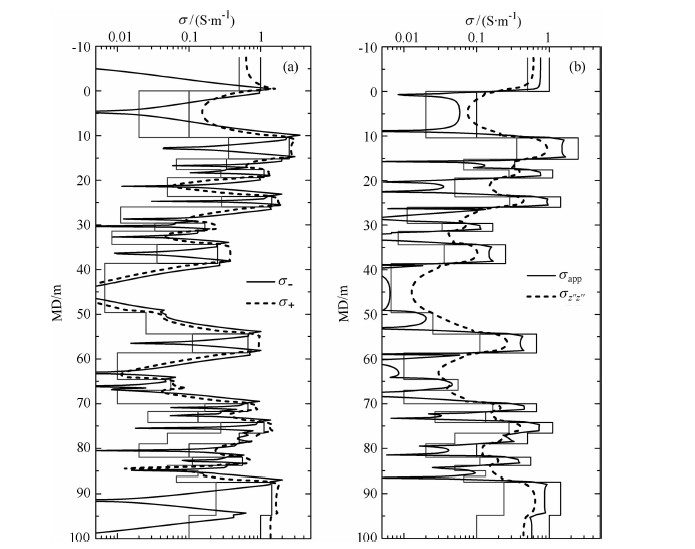
图 7 各向异性Oklahoma地层模型中的组合曲线 Fig. 7 The combination curves in TI Oklahoma model |
Oklahoma地层模型是检验电法测井资料处理方法的经典各向同性模型,为进一步检验本文的三维感应测井资料处理方法,我们将其中电导率较高的地层推广为各向异性层.图 7给出了包含各向异性地层的Oklahoma模型三条组合曲线的处理结果.组合曲线σapp的纵向分辨率比σz″z″有明显改善,响应值与地层水平电导率更接近;结合组合曲线σ-可以确定出地层纵向边界位置,包括小反差的高阻层和层厚小于1.0m的薄层.靠近围岩的各向异性厚层中组合曲线σ+明显偏离零,而中间的高阻各向同性层中σ+响应值则接近零,为各向异性厚层的识别提供了判断依据.
4 结论本文利用广义反射系数法推导了水平层状各向异性介质中电磁场的积分解析解,并利用快速汉克尔变换技术实现了其快速计算.三种模式波的递推公式可以写成统一的表达形式,推导过程简明.通过与已发表的计算结果相比较,验证了本文公式推导的正确性.倾斜井中数值模拟结果显示了线圈坐标系下的实测曲线响应行为复杂,很难由原始的测井曲线直观提取地层参数信息.本文利用实测曲线构造了响应行为更加规则的三条组合曲线,简化了测井响应与地层参数之间的关系,实现了三维感应测井响应资料的初步直观解释.
附录A 发射源所在层纵向行波的表达式令发射源所在层为第m层,由(1)式,任意层n的电磁场法向分量可表示为:
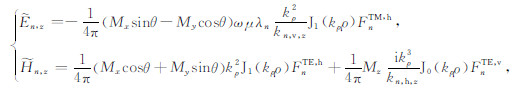
|
(A1) |
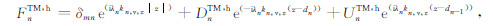
|
(A2) |

|
(A3) |
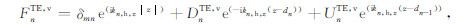
|
(A4) |
其中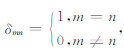
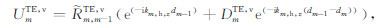
|
(A5) |
同理,在边界z=dm处有:
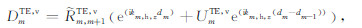
|
(A6) |
联立式(A4)和(A5)求解UmTE,v和DmTE,v有:
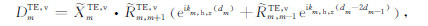
|
(A7) |

|
(A8) |
其中
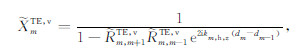
|
(A9) |
将式(A6)-(A8)代入式(A4),经整理得:
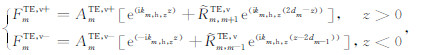
|
(A10) |
其中AmTE,v+和AmTE,v-的具体表达式见(7a)-(7c).重复上面的推导过程,式(A2)可改写为:
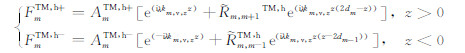
|
(A11) |
其中AmTM,h+和AmTM,h-的具体表达式见(9a)-(9c).式(A3)可改写为:
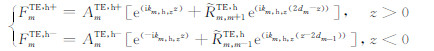
|
(A12) |
其中AmTE,h+和AmTE,h-的具体表达式见(8a)-(8c).式(A10)-(A12)除指数因子外,表达形式相同,略去相应的上角标,可将统一写成表达式(6).
| [1] | 党瑞荣, 秦瑶, 谢雁, 等. 三分量感应测井系统研究. 石油地球物理勘探 , 2006, 41(4): 484–488. Dang R R, Qin Y, Xie Y, et al. Study of 3-C induction log system. Oil Geophysical Prospecting (in Chinese) , 2006, 41(4): 484-488. |
| [2] | Klein J D, Martin P R, Allen D F. The petrophysics of electrically anisotropic reservoirs. The Log Analyst , 1997, 38(3): 25-36. |
| [3] | Zhang Z Y, Yu L, Kriegsmauser B, et al. Simultaneous determination of relative angles and anisotropic resistivity using multicomponent induction logging data. SPWLA 42nd Annual Logging Symposium, Houston, 2001. http://www.oalib.com/references/19002510 |
| [4] | 王昌学, 周灿灿, 储昭坦, 等. 电性各向异性地层频率域电磁响应模拟. 地球物理学报 , 2006, 49(6): 1873–1883. Wang C X, Zhou C C, Chu Z T, et al. Modeling of electromagnetic responses in frequency domain to electrical anisotropic formations. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1873-1883. |
| [5] | Davydycheva S, Druskin V, Habashy T. An efficient finite-difference scheme for electromagnetic logging in 3D anisotropic in homogeneous media. Geophysics , 2003, 68(5): 1525-2536. DOI:10.1190/1.1620626 |
| [6] | 孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应. 地球物理学报 , 2008, 51(5): 1600–1607. Sun X Y, Nie Z P, Zhao Y W, et al. The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1600-1607. |
| [7] | Lv W G, Chu Z T, Zhao X Q, et al. Simulation of electromagnetic wave logging response in deviated wells based on vector finite element method. Chinese Physics Letters , 2009, 26(1): 96-99. |
| [8] | 汪宏年, 陶宏根, 姚敬金, 等. 用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应. 地球物理学报 , 2008, 51(5): 1591–1599. Wang H N, Tao H G, Yao J J, et al. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1591-1599. |
| [9] | Wang H N, Tao H G, Yao J J, et al. Fast multiparameter reconstruction of multicomponent induction well-logging datum in a deviated well in a horizontally stratified anisotropic formation. IEEE Transactions on Geoscience and Remote Sensing , 2008, 46(5): 1525-1534. DOI:10.1109/TGRS.2008.916080 |
| [10] | Wei B J, Zhang G J, Liu Q H. Recursive algorithm and accurate computation of dyadic Green's functions for stratified uniaxial anisotropic media. Sci. China Inf. Sci. , 2008, 51(1): 63-80. DOI:10.1007/s11432-007-0069-7 |
| [11] | Zhong L L, Li J, Bhardwaj A, et al. Computation of triaxial induction logging tools in layered anisotropic dipping formations. IEEE Trans. Geosic. Remote. Sens. , 2008, 46(4): 1148-1163. DOI:10.1109/TGRS.2008.915749 |
| [12] | 范宜仁, 杨震, 邓少贵, 等. 层状介质中大斜度井感应测井响应计算新方法. 西南石油大学学报(自然科学版) , 2009, 31(1): 166–169. Fan Y R, Yang Z, Deng S G, et al. New computation method of induction logging response of highly-deviated wells in stratified media. Journal of Southwest Petroleum University (Science & Technology Edition) (in Chinese) , 2009, 31(1): 166-169. |
| [13] | 魏宝君, 王甜甜, 王颖. 用磁流源并矢Green函数的递推矩阵方法计算层状各向异性地层中多分量感应测井响应. 地球物理学报 , 2009, 52(11): 2920–2928. Wei B J, Wang T T, Wang Y. Computing the response of multi-component induction logging in layered anisotropic formation by the recursive matrix method for magnetic-current-source dyadic Green's function. Chinese J. Geophys. (in Chinese) , 2009, 52(11): 2920-2928. |
| [14] | 姚东华, 汪宏年, 杨守文, 等. 用传播矩阵法研究层状正交各向异性地层中多分量感应测井响应. 地球物理学报 , 2010, 53(12): 3026–3037. Yao D H, Wang H N, Yang S W, et al. Study on the responses of multi-component induction logging tool in layered orthorhombic anisotropy formations by using propagator matrix method. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 3026-3037. |
| [15] | Andersion W L. Computer program:numerical integration of related Hankel transforms of orders 0 and 1 by adaptive digital filtering. Geophysics , 1979, 44(7): 1287-1305. DOI:10.1190/1.1441007 |
| [16] | Wang H, Barber T, Morriss C, et al. Determining anisotropic formation resistivity at any relative dip using a multiarray triaxial induction tool.//SPE 103113 presented at the 2006 SPE Annual Technical Conference and Exhibition:San Antonio, Texas, U. S. A., 2006. |
| [17] | Barber T, Andersion B, Abubakar A, et al. Determining formation resistivity anisotropy in the presence of invasion.//SPE 90256 presented at the 2004 SPE Annual Technical Conference and Exhibition:Houston, Texas, U. S. A., 2004. |
| [18] | Moran J H, Gianzero S. Effects of formation anisotropy on resistivity-logging measurements. Geophysics , 1979, 44(7): 1266-1286. DOI:10.1190/1.1441006 |
| [19] | Chen W C. Waves and Fields in Inhomogeneous Media. New York: Van Nostrand Reinhold, 1990 : 48 -65. |
| [20] | 陈桂波, 汪宏年, 姚敬金, 等. 水平层状各向异性介质中电磁场并矢Green函数的一种高效算法. 物理学报 , 2009, 58(3): 1608–1618. Chen G B, Wang H N, Yao J J, et al. An efficient algorithm of the electromagnetic dyadic Green's function in a horizontal-layered anisotropic medium. Acta Physica Sinica (in Chinese) , 2009, 58(3): 1608-1618. |
| [21] | Zhang Z Y, Yu L M, Kriegsmauser B, et al. Simultaneous determination of relative angles and anisotropic resistivity using multicomponent induction logging data.//SPWLA 42nd Annual Logging Symposium, Houston, 2001, Paper Q. |
| [22] | Mallan R K, Torres-Verdin C. Effects of geometrical, environmental, and petrophysical parameters on multi-component induction measurements acquired in high-angle wells. Petrophysics , 2007, 48(4): 271-288. |
| [23] | Kennedy D, Peksen E, Zhdanov M. Foundations of tensor induction well-logging. Petrophysics , 2001, 44(6): 588-610. |
| [24] | Wang H M, Barber T, Rosthal R, et al. Fast and rigorous inversion of triaxial induction logging data to determine formation resistivity anisotropy, bed boundary position, relative dip and azimuth angles.//SEG International Exposition and Seventy-Third Annual Meeting, 2003, 22. |
| [25] | Minerbo G N, Omeragic D, Rosthal R A. Directional electromagnetic measurements insensitive to dip and anisotropy. Patent US6969994 B2, 2005. http://www.oalib.com/references/19002513 |
 2013, Vol. 56
2013, Vol. 56


