2. 中国石油大学(华东)CNPC测井重点实验室, 青岛 266580
2. CNPC Key Laboratory for Well Logging, China University of Petroleum, Qingdao 266580, China
储层饱和度的计算与水淹层水淹级别的判定很大程度上依赖于地层水电阻率的准确获取[1],而地层水电阻率的确定一直是困扰储层测井评价的难题,自然电位测井是反映储层渗透性的重要测井方法,也是最能反映原状地层水矿化度的重要信息.储层的自然电动势包括:扩散电动势、扩散吸附电动势(薄膜电位)、电流电位、氧化-还原电位,其中电流电位与氧化-还原电位较为微弱,可以忽略,渗透层的自然电位主要由薄膜电位所产生,而薄膜电位主要取决于泥浆滤液与地层水矿化度的比值[2].薄膜电位产生于泥浆滤液与地层水的交界面上,也即储层矿化度剖面的突变处,对储层泥浆侵入过程进行模拟与分析,有助于还原储层流体分布形态,确定薄膜电位产生位置.
近年来,斯伦贝谢、贝克休斯、哈里伯顿等公司分别推出了阵列感应成像测井仪(AIT)、高分辨率感应测井仪(HDIL)、高分辨率阵列感应测井仪(HRAI)等阵列型感应测井仪器[3-4],可以提供具有相同分辨率、不同探测深度的5/6条曲线[5-7],基于具有丰富信息的阵列感应测井数据,建立适当的地层模型与合理的算法,可以很好地重构地层电阻率分布剖面、确定薄膜电位产生位置,结合自然电位测井,可以有效地联合反演地层水电阻率.笔者通过对泥浆侵入过程进行数值模拟,分析了薄膜电位的产生位置,提出了“五参数”地层模型,进而基于阵列感应与自然电位联合反演,重构了地层电阻率分布剖面,精确求取了地层水电阻率.
2 泥浆侵入模拟与薄膜电位产生位置确定 2.1 泥浆侵入数值模拟储层泥浆侵入包括泥浆滤液对地层油气的驱替、泥浆滤液与地层水离子的扩散两个相互独立的过程[8-9],分别体现为泥浆侵入过程中储层径向上饱和度与矿化度的变化,而储层径向上流体性质的变化造成了储层径向电阻率分布的变化.假设两相流体的渗流满足达西定律,储层中岩石和流体微可压缩,考虑毛管压力和重力,则两相渗流方程为:
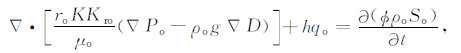
|
(1) |
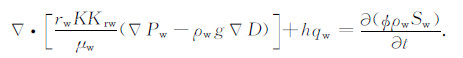
|
(2) |
其中,Pw、Po分别表示水相和油相压力,So、Sw分别表示含油、水饱和度,μo、μw分别表示油、水黏度,K为地层绝对渗透率,Kro、Krw分别表示油、水两相的相对渗透率,ϕ为地层孔隙度,qo、qw分别表示油、水产量(采出为负,注入为正),h为地层厚度,g为重力加速度,ρo、ρw分别为油和水的密度.泥浆滤液与地层水盐离子的扩散方程表述为:
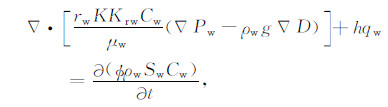
|
(3) |
式中Cw为地层水(或泥浆滤液)矿化度.同时,结合Archie公式:

|
(4) |
式中a、b、m、n为阿尔奇参数,Rw为地层水(或泥浆滤液)电阻率.
建立适当的地层模型,利用有限差分的方法,即可实现对泥浆侵入过程中储层饱和度、矿化度、电阻率分布的数值模拟.
2.2 薄膜电位产生位置分析为了研究不同流体类型储层泥浆侵入过程中井周流体与电阻率分布特征,建立了典型的油层、水层与油水同层模型,并对不同模型泥浆侵入过程中,储层饱和度、矿化度、电阻率剖面进行了模拟(图 1).模型条件:地层孔隙度10%,渗透率100 μm2,地层水矿化度80000 mg/L,泥浆滤液矿化度44000 mg/L,残余油20%,束缚水20%.油层:含油饱和度75%;水层:含油饱和度25%;油水同层含油饱和度50%.

|
图 1 不同流体类型储层泥浆侵入特征 (a)油层;(b)水层;(c)油水同层. Fig. 1 Mud invasion characteristics of different reservoir types (a)Oillayer; (b)Waterlayer; (c)Oil-waterlayer. |
由不同流体类型储层饱和度、矿化度、电阻率分布形态可以看出:
①泥浆侵入过程中,饱和度与矿化度沿径向方向单调变化,且驱替作用与扩散作用向地层深处推进速度不同,而电阻率的非单调变化正是由于两种作用的速度差;
②饱和度变化受地层原始含水饱和度影响较大,随着原始含水饱和度的增加,驱替深度逐渐变浅;
③矿化度变化受地层含水饱和度影响较小,相对饱和度缓慢的变化剖面,矿化度变化剖面存在阶梯状突变;
④薄膜电位产生于矿化度突变的阶梯处,在电阻率剖面上,油层为上升的阶梯处,水层为下降的阶梯处,油水同层为“低阻环”的下降处.
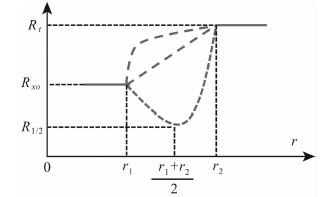
3 “五参数”地层模型根据泥浆侵入过程中储层径向电阻率复杂的分布形式[10],构造井周电阻率近似分布模型如图 2.
|
图 2 五参数地层模型 Fig. 2 Schematic diagram of 5-parameter formation model |
模型表达式为:
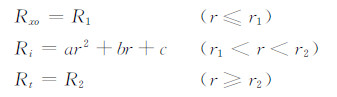
|
(5) |
其中:Rxo=R1为冲洗带电阻率,r1为冲洗带半径,r2为过渡带半径,r1和r2(r2≥r1)之间为过渡带,Rt=R2为原状地层电阻率,Ri为过渡带电阻率,假设过渡带电阻率按抛物线分布:Ri=ar2+br+c,其中,r为径向深度,a、b、c为抛物线系数,由(r1,R1)、(r2,R2)和((r1+r2)/2,R1/2)三点确定,其中R1/2表示过渡带中点位置的地层电阻率.五参数(r1,r2,R1,R2,R1/2)确定的地层电阻率分布,反映了储层泥浆侵入特性,决定了地层的电测井响应.
“五参数”模型中,当过渡带抛物线系数a=0时,即退化为斜坡状“四参数”模型,当r1≈r2时,即退化为活塞状“三参数”模型,通过系数的调整,可实现对包括“低阻环”在内的各种储层电阻率分布形态的表征.
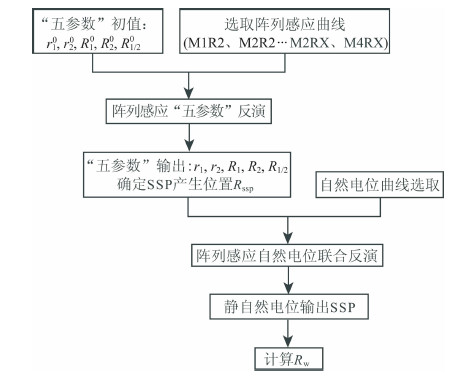
4 阵列感应与自然电位联合反演地层水电阻率求取过程中,基于阵列感应与自然电位测井资料,采用物理参数相结合的联合反演方法,首先基于“五参数”地层模型,重构储层电阻率剖面,确定自然电位产生位置,进而将储层电阻率与自然电位产生位置(Rssp)作为已知参数,结合泥浆滤液电阻率,利用自然电位测井,对地层水电阻率进行反演.为消除上下围岩的影响,反演一般从泥岩层开始,采用深度域开窗的方法,一次反演覆盖目标层上下多个层,对多层数据同时进行反演,具体流程图见图 3.
|
图 3 阵列感应与自然电位联合反演流程图 Fig. 3 Flowchart of array induction and spontaneous potential joint inversion |
地层参数x决定了储层测井响应,用数学函数表示为:
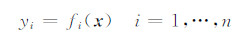
|
(6) |
其中,x为地层参数向量,yi为(阵列感应或自然电位)第i个测井响应.利用测井响应反演地层参数x,问题可归结为最小二乘问题:
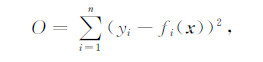
|
(7) |
方程(7)可转化为
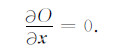
|
(8) |
通过Taylor公式对非线性方程线性化:
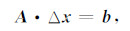
|
(9) |
为提高算法的收敛性和稳定性,采用阻尼正则化的方法对(9)式进行求解,
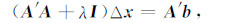
|
(10) |
其中Δx为待反演参数增量列阵,λ为正则化因子,一般采用数值试验的方法获得,本文中选2,A为雅克比矩阵.
4.1 阵列感应反演算法以贝克休斯高分辨率感应测井仪(HDIL)为例,仪器共能为现场提供3组分辨率(M1-0.3 m、M2-0.6 m、M4-1.2 m)、6种探测深度(R1-0.25 m、R2-0.5 m、R3-0.75 m、R6-1.5 m、R9-2.3 m、RX-3.0 m)的电阻率曲线,考虑到阵列感应信号合成原理与HDIL经常存在过聚焦现象[11],反演过程舍弃了M2R1(0.6 m分辨率0.25 m探测深度)曲线,同时引入合成中处理较少的M1R2(0.3 m分辨率0.5 m探测深度)与M4RX(1.2 m分辨率3.0 m探测深度)曲线进行反演.假设深度窗口内共M层地层,基于N(N≥M)个深度点阵列感应测井响应进行反演,雅克比矩阵表达式为:
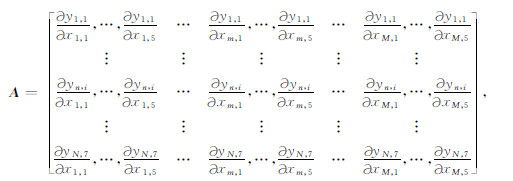
|
(11) |
其中yn,i为第n个深度处第i条阵列感应测井曲线,xm,1,xm,2,…,xm,5为第m层储层五参数r1m,r2m,R1m,R2m,R1/2m.反演过程中,雅克比矩阵的计算占用了主要的时间,为了加快反演速度,文中采用如下方法计算阵列感应反演矩阵A.假设介质横向电导率是分段连续的,则感应测井视电导率可表述为:
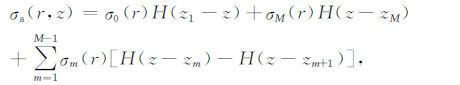
|
(12a) |
σ0(r)、σM(r)、σm(r)为每层的电导率,可用如下公式确定:
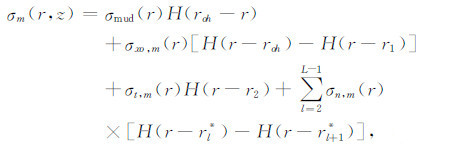
|
(12b) |
其中H为Heaviside函数、roh为井眼半径、r l*(l=2,3,…,L)为r1、r2之间的离散点,且r1*=r1、rL*=r2.又由
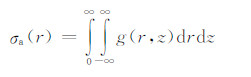
|
(13) |
可得:

|
(14) |
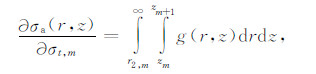
|
(15) |
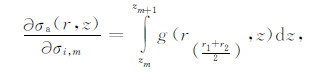
|
(16) |
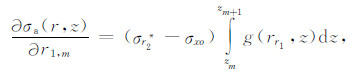
|
(17) |
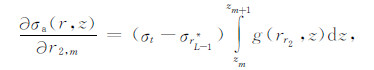
|
(18) |
其中,g(r,z)为阵列感应二维几何因子.HDIL等阵列感应测井仪器软件聚焦过程中已消除了趋肤效应等影响,可以采用信号合成过程中二维目标函数作为反演的几何因子.由于g(r,z)事前已知,因此,每次计算时无需反复计算响应的几何因子,大大减少了计算量.
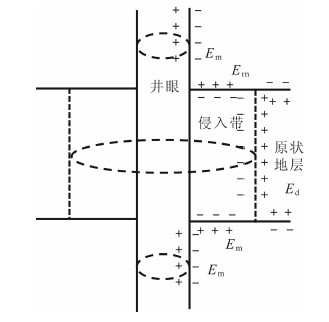
4.2 自然电位反演算法在钻井过程中,由于钻井液与地层水矿化度的差异及地层岩性的差异,不同矿化度溶液界面上会产生偶极子层,由自然电位测井原理可知,自然电位的偶极子源分布在井壁与不同地层的边界上,自然电位测井模型图见图 4.
|
图 4 自然电位测井模型图 Fig. 4 Schematic diagram of spontaneous potential logging |
文中对自然电位测井采用直接反演算法,即由自然电位测井响应直接计算雅克比矩阵,在自然电位测井中,如果偶极子均匀地分布在界面上,可以用电流源的方式进行处理[12],电场满足方程为:
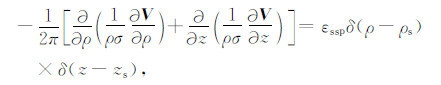
|
(19) |
其中V为电流势,εssp为静自然电位.对于M层地层,第n个深度处自然电位响应(SPn)为M个静自然电位源产生响应的叠加,可以表示为:
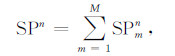
|
(20) |
其中:SPmn为第m个静自然电位源(εsspm)在n点处产生的自然电位响应.定义泛函:
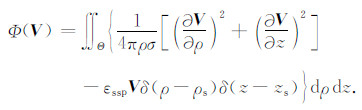
|
(21) |
利用有限元法即可对(21)式进行快速求解,进而可快速计算SPn.
4.3 地层水电阻率(Rw)获取岩性较纯的砂岩层段,当地层水主要为NaCl溶液时,地层自然电动势最大值,即静自然电位(εssp)决定于泥浆滤液电阻率与地层水电阻率的比值,可由如下公式确定[13]:
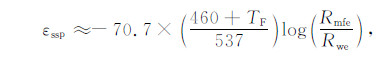
|
(22) |
其中TF为华氏温度,Rmfe为等效泥浆滤液电阻率,Rwe为等效地层水电阻率,可通过图版法转化为地层水电阻率[14-15]:
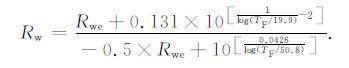
|
(23) |
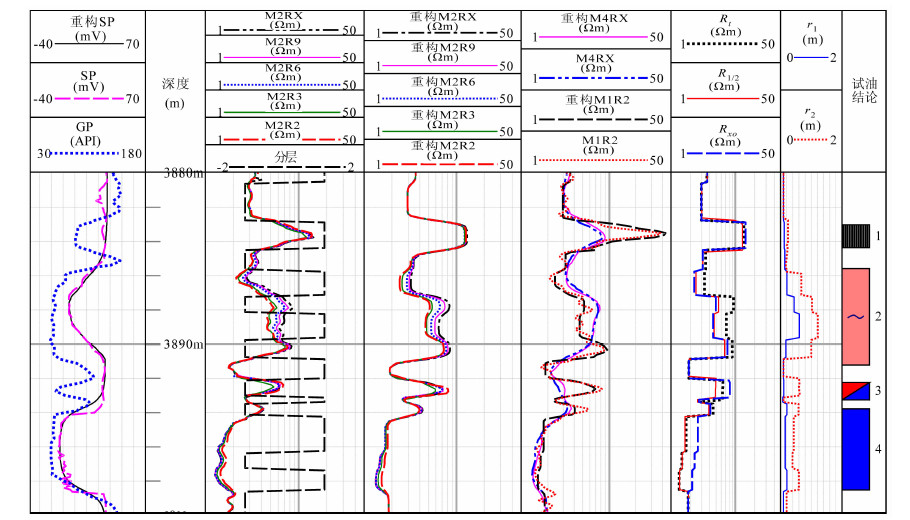
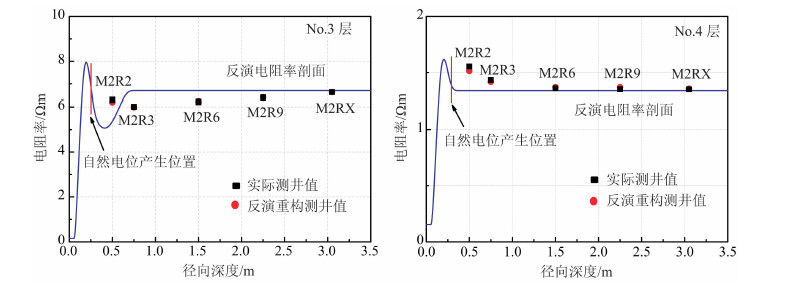
选取中国西部某油田X井段处理结果进行分析,该井段深度为3880 m至3900 m(图 5),井眼直径为0.2 m,泥浆电阻率为0.154 Ωm,泥浆密度为1.2g/cm3,地层温度为101.3 ℃.实测阵列感应曲线与分层曲线如第3道所示,通过活度法实现了基于阵列感应曲线的自动分层与特征值自动读取.“五参数”反演能直观地显示储层径向电阻率的变化与侵入深度(第5、6道),并可对储层径向非线性电阻率剖面进行重构,图 6中给出了No.3层、No.4层3897.38~3898.56 m储层电阻率剖面图.基于反演结果,确定了薄膜电位产生位置(图 6红线).基于阵列感应与自然电位联合反演获取No.2层与No.4层静自然电位(εssp)均为-44 mV,表明两层物性较好且具有相同的地层水矿化度.由于地层电阻率的差异,造成油层自然电位响应(-34.1 mV)明显低于下部水层(-43.3 mV),获取地层水矿化度为64282 mg/L,地层水分析矿化度为64443.13 mg/L,反演结果与水分析资料能很好地符合,实测与重构SP曲线如第1道,重构阵列感应测井曲线如第4道,重构结果与实测结果均能很好的吻合,验证了算法的正确性.
|
图 5 X井阵列感应与自然电位联合反演效果图 Fig. 5 Results of joint inversion of array induction and spontaneous potential loggingin X well |
|
图 6 No.3和No.4层反演结果与阵列感应测井数据对比 Fig. 6 Comparison of the inverted invasion profile(blue curve)and the measured resistivity from the HDIL (scattered pink points)for layers No.3 and No.4 |
同时,地层径向电阻率的反演重构有利于储层流体性质的识别,如图中No.3层视电阻率与上部No.2层相近,但反演泥浆侵入剖面有明显的“低阻环”特征(R1/2 < Rt < Rxo),原状地层电阻率明显低于No.2层,为典型的油水同层显示,因此解释为油水同层,与试油结果吻合;No.2层为典型低侵特征,原状地层电阻率较高,为油层指示;No.4层为典型高侵特征,原状地层电阻率较低,为水层指示.解释结论均与试油结论吻合,径向电阻率剖面的重构能为储层流体性质的识别提供有力支持.
为了进一步验证算法的正确性与适用性,对某区块18个岩性较纯的砂岩层进行了联合反演,并求取了地层水矿化度,部分反演结果与水分析对比结果如表 1所示.基于阵列感应与自然电位联合反演精确求取了该区块地层水矿化度,反演结果与水分析结果相近,反演计算结果表明:本区块地层水矿化度分布在85000~100000 mg/L.
|
|
表 1 联合反演地层水矿化度与水分析结果对比表 Table 1 Comparisonofwatersalinitiesofjointinversionandwateranalysisresults |
地层水矿化度的获取保证了储层饱和度的精确计算,特别是对于(天然)水淹层及缺少地层水资料的区块,联合反演提供了一种可行的储层评价手段,为复杂储层评价提供了保障.
6 结论淡水泥浆侵入过程中,饱和度与矿化度变化推进速度差异造成了储层径向电阻率的非线性变化,油层薄膜电位产生于电阻率上升的阶梯处,水层为下降的阶梯处,油水同层为“低阻环”的下降处;
“五参数”模型能表征包括“低阻环”在内的各种储层电阻率分布形态,阵列感应与自然电位联合反演能重构储层电阻率分布剖面,确定自然电位产生位置,精确计算原状地层水电阻率,为储层流体识别提供依据;
阵列感应与自然电位联合反演算法稳定、可靠,反演结果与水分析结果一致,为(天然)水淹层与缺乏地层水分析资料区块储层测井评价提供了依据.但当储层泥质含量较高或地层水不以NaCl为主要成分时,反演算法仍需进一步讨论与改进.
| [1] | 张庚骥. 电法测井. 北京: 石油工业出版社, 1984 . Zhang G J. Electrical Logging (in Chinese). Beijing: Petroleum Industry Presss, 1984 . |
| [2] | 潘克家, 谭永基. 复杂地层中自然电位测井的高效数值模拟. 石油地球物理勘探 , 2009, 44(3): 371–376. Pan K J, Tan Y J. High-efficient numeric simulation of spontaneous potential log in complex beds. Oil Geophysical Prospecting (in Chinese) , 2009, 44(3): 371-376. |
| [3] | Strickland R W, Gulamabbas A M, Randal T B. High resolution array induction tool:US, 6597993. 2003-07-22. |
| [4] | Sinclair P L. Multi-frequency array induction tool:US, 6603312. 2003-08-05. http://www.freepatentsonline.com/6603312.html |
| [5] | Barber T D, Rosthal R A. Using a Multiarray induction tool to achieve high-resolution logs with minimum environmental effects.//SPE 66th Annual Technical Conference and Exhibition, Dallas, Texas, USA, 6-9 October 1991. http://www.onepetro.org/mslib/servlet/onepetropreview?id=00022725. |
| [6] | 张业荣, 聂在平, 漆兰芬. 地层电导率非线性反演方法--阵列感应数据反演. 测井技术 , 1997, 21(5): 305–309. Zhang Y R, Nie Z P, Qi L F. A nonlinear inversion approach to formation conductivity-Inversion of AIT measurements. Well Logging Technology (in Chinese) , 1997, 21(5): 305-309. |
| [7] | Gao G Z, Torres-Verdin C. Fast inversion of borehole array induction data using an inner-outer loop optimization technique.//SPWLA 44th Annual Logging Symposium, Texas, USA, 2003. http://www.onepetro.org/mslib/servlet/onepetropreview?id=SPWLA-2003-TT. |
| [8] | Wu J H, Torres-Verdin C, Sepehrnoori K, et al. Numerical simulation of mud-filtrate invasion in deviated wells. SPE Reservoir Evaluation & Engineering , 2004, 7(2): 143-154. |
| [9] | Navarro D, Li S J, Liu R C, et al. Invasion effects on time-lapsed array induction logs.//SPWLA 48th Annual Logging Symposium, Austin, Texas, USA, 2007. http://www.spwla.org/publications/view/item/3092. |
| [10] | Deng S G, Sun Q T, Li H, et al. The sensitivity of the array resistivity log to mud filtrate invasion and its primary five-parameter inversion for improved oil water recognition. Petroleum Science , 2012, 9(3): 295-302. DOI:10.1007/s12182-012-0212-y |
| [11] | Chew W C, Liu Q H. Inversion of induction tool measurements using the distorted Born iterative method and CG-FFHT. IEEE Transactions on Geoscience and Remote Sensing , 1994, 32(4): 878-884. DOI:10.1109/36.298015 |
| [12] | Zhang G J, Wang G L. Application of vector potential theory to spontaneous potential computation. Radio Science , 1997, 32(3): 899-905. DOI:10.1029/97RS00050 |
| [13] | Pirson S J. Handbook of Well Log Analysis:for Oil and Gas Formation Evaluation. Englewood Cliffs:Prentice-Hall, 1963. |
| [14] | Schlumberger. Log Interpretation Charts. Houston: Schlumberger Educational Services, 1991 . |
| [15] | Bigelow E L. Introduction to Wireline Log Analysis. Houston: Western Atlas International, 1992 . |
 2013, Vol. 56
2013, Vol. 56

