近年来,利用油气储层中流动电位的频散特性研究油气藏的地层信息与储渗特性已引起地球物理领域的关注[1-5],在油气勘探中的震电效应,其理论基础之一就是流体饱和孔隙介质中的频率域流动电位效应.流动电位频散特性的研究对于分析地震波及声波在地下传播过程中产生的电磁信号具有极其重要的意义[6-8].
目前有关流动电位微观机制的理论,是基于Kvink在1850年提出的固相和液相边界存在双电层的假设.Ishido等[9]选取圆直毛细管模型,给出了稳恒条件下孔隙介质中动电耦合系数的明确表达式.Pride等[10]利用平板型孔隙模型,得到了孔隙介质中动电耦合系数与频率的关系式,分析了振动波和电磁波的耦合特性与频率的关系.Pride[11]从固相颗粒和孔隙溶液各自服从的基本原理出发,采用平均体积法导出了弹性波和电磁波的耦合特性与频率的关系式.Pride通过物理化学概念建立的动电耦合理论是正确的,但是没有进行储层岩石孔隙参数和电化学参数对动电效应影响的模拟计算和实验验证.Ken等[12]研究了一个圆直毛管中表面双电层对电动过程的影响,解析计算了双电层电位、电渗流速度和电荷密度在毛管截面上的分布,分析了电解质溶液、毛管半径和双电层结构对电渗流过程的影响. Reppert等[13-14]利用单个圆直毛细管模型研究了周期性流动电位的频率特性和周期性电渗流的流动特性,所采用的研究方法具有重要的理论意义.Yang等[15]利用圆直毛细管模型,导出了谐变条件下流体流速的达西定律和电流密度的欧姆定律,系统地建立了圆直毛细管中频率域渗流场与电流场的相互耦合理论,其复数形式的数学方法具有重要的实用价值,但是仍无法定量描述储层岩石孔渗特性和阳离子交换量等各个因素对流动电位频散特性的影响. Kang等[16]在微球填充的微通道内,利用单个圆直毛细管模型研究了交变电流驱动下周期性电渗流的流动特性.Saunders等[17]建立了在电场和流体压力场作用下油藏中油水两相流各自满足的广义达西定律和欧姆定律,给出了稳恒条件下油水两相流的动电耦合系数.Revil等[18]利用体积平均方法分析了非饱和含水孔隙介质水相-不导电流体相两相流体的动电耦合效应.Linde等[19]给出了油水两相流的流动电流与含水饱和度等储渗参数的关系式,并进行了实验验证.Jackson[20]利用毛管束模型分别建立了水润湿和油润湿两种情况下油水两相流的流动电位相对耦合系数,并理论计算了流动电位相对耦合系数与含水饱和度的关系,分析了润湿性的影响.龚磊等[21]研究了包含电黏性效应的二维微通道周期流动诱导电场和速度的解析表达式.王军等[22]根据孔隙介质的动电耦合理论设计了一套岩芯渗透率测量系统,验证了利用动电效应测量岩芯渗透率的可行性.
资料分析表明,尽管流动电位特性及相关技术已被研究多年,但是大多数工作集中在稳恒条件下的流动电位特性,仅有很少部分的工作涉及到周期性流动电位的频散特性;另外,研究结果多数集中在对单个毛细管模型的研究,所得结果并不能用于储层的定量解释;同时,有关随时间谐变条件下流动电位的研究,国外做的实验研究比较多,但还不能揭示储层岩石储渗特性与流动电位的定量关系,而国内对此方面的研究还比较缺乏.至今,有关储层岩石周期性流动电位频散特性的理论研究,还没有形成成熟、系统、有普遍指导意义的理论方法和数学模型,其微观机理的解释还不一致,还无法定量解释储层岩石储渗特性和阳离子交换量等各个因素对流动电位频散特性的影响,制约了相关技术的推广与应用.
本文将依据圆直毛管模型,建立谐变信号激励下渗流场与电流场的耦合理论,定量描述含水储层岩石流动电位的频散特性,数学模拟频率域储层岩石动电耦合系数和流动电位耦合系数随储层岩石孔隙结构参数、地层水性质、阳离子交换量以及谐变频率等的变化规律.
2 储层岩石中流动电位的耦合模型 2.1 储层岩石的双电层电位理论将储层岩石模拟为平行排列的圆直毛管束模型,圆直毛管模型微观参数与储层岩石宏观参数的对应关系为

|
(1) |
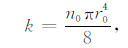
|
(2) |
式中,φ为孔隙度,k为渗透率,n0为单位面积上的毛管数,r0为毛管的半径.
储层岩石骨架与溶液中离子相互作用在交界面处形成双电层结构,在半径为r0的长直毛细管中,多元电解质溶液形成的离子浓度分布为
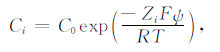
|
(3) |
式中,Ci为组分i的浓度,C0为溶液初始浓度,F=9.65×104C·mol-1为法拉第常数,Zi为组分i的价数,ψ为双电层形成的电位,R=8.314J·(k·mol)-1为气体普适常数,T为绝对温度.
在Z-Z价对称地层水溶液中,毛管内的电荷密度:
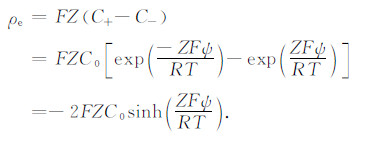
|
(4) |
毛细管内的电位分布满足泊松方程[23]:
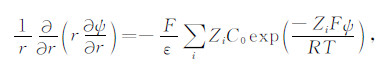
|
(5) |
式中,ε为溶液的介电常数.对于储层岩石,双电层的厚度λD要远小于毛管半径r0,即r0≫λD,因此毛管中大部分区域ψ很小,所以
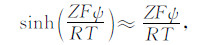
|
(6) |
此时,泊松方程化简为
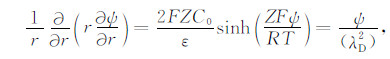
|
(7) |
式中,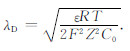
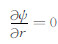
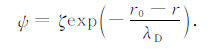
|
(8) |
此时,式(3)可以表示为

|
(9) |
假设在孔隙中流体的流动满足Navier-Stokes方程:
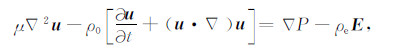
|
(10) |
式中,ρ0为孔隙中流体的密度,P为流体压力.令电场强度E=-▽U,U为流动电位,u为流速,μ为流体黏度.
因为储层岩石中流体流动满足不可压缩条件:
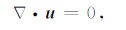
|
(11) |
即
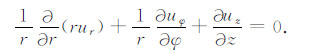
|
(12) |
又因为u=uzez,ez为毛管轴向方向的单位矢量,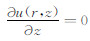
假设在岩石孔隙中沿z方向由弹性波引起的压力梯度为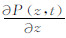
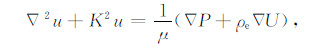
|
(13) |
其中,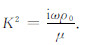
将式(4)代入式(13),得
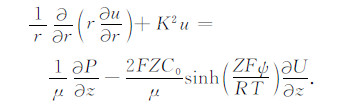
|
(14) |
式(14)左右两边同时乘以r2,则
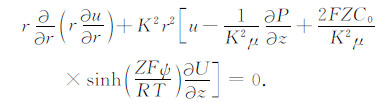
|
(15) |
根据Bessel方程的定义,当K2 ≠ 0时,方程(15)的通解为
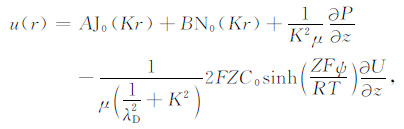
|
(16) |
式中,J0(Kr)为零阶第一类贝塞尔函数,N0(Kr)为零阶第二类贝塞尔函数.利用电位边界条件和流速边界条件:①在r=0处,u为有限值,则有B=0;②当r=r0时,u=0,则有
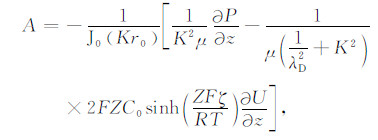
|
(17) |
将式(6)代入式(17),得
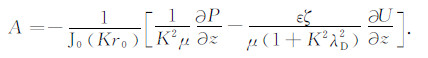
|
(18) |
于是式(16)表示为
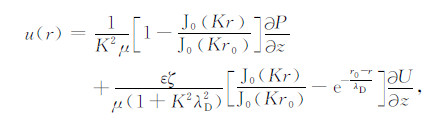
|
(19) |
其中,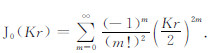
将此速度分布沿毛管截面积分,得单根毛管中的流量:
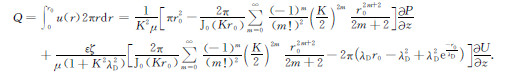
|
(20) |
根据平行毛管束模型,毛管半径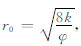
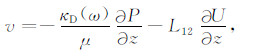
|
(21) |
式(21)为频率域储层岩石中渗流流速的达西定律,L12
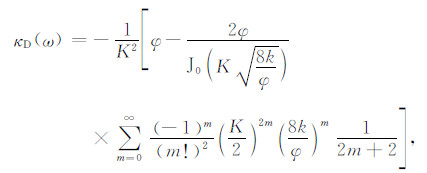
|
(22) |
L12为电动耦合系数:
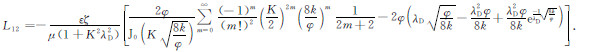
|
(23) |
对于稀溶液,毛管内溶液第i组分的摩尔通量:
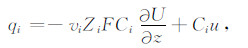
|
(24) |
式中,vi为第i组分离子迁移率.将式(3)代入式(24),得
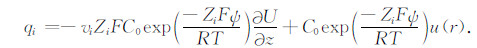
|
(25) |
将式(19)代入式(25),利用式(9)的级数展开形式,将式(25)沿毛管截面积分,得出单根毛管第i组分离子流密度为

|
(26) |
根据平行毛管束模型,单位面积内毛管的离子流量Wi=n0wi,即储层岩石第i组分离子流密度:
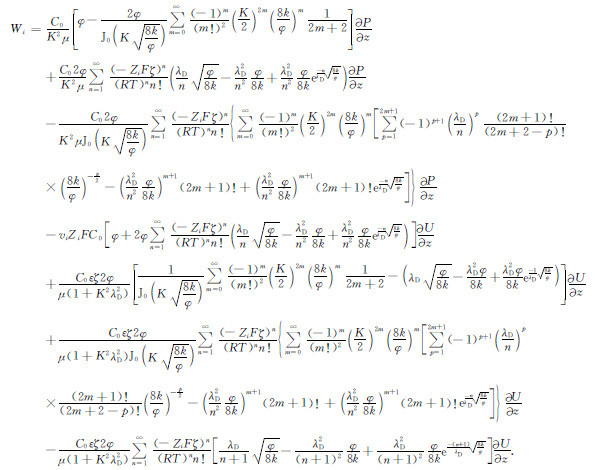
|
(27) |
由电流密度的定义式,得毛管内电流密度:
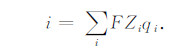
|
(28) |
将式(28)沿毛管截面积分,然后根据平行毛管束模型,得储层岩石中电流密度:

|
(29) |
将式(27)代入式(29),得
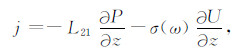
|
(30) |
式(30)为频率域储层岩石中电流密度的欧姆定律,L21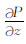
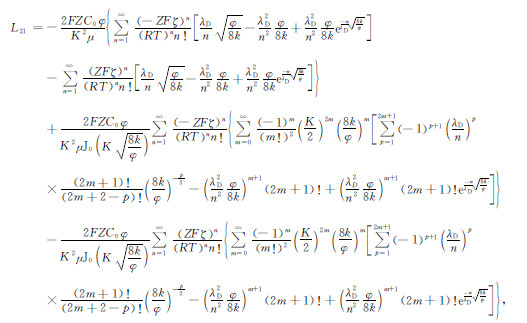
|
(31) |
σ(ω)为复电导率:
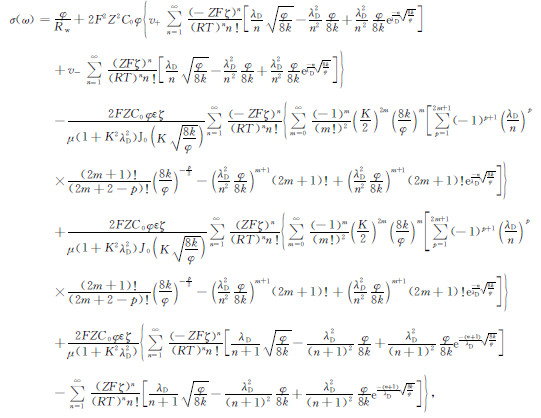
|
(32) |
其中,Rw=[F2Z2C0(v++v-]-1为地层水溶液的电阻率.式(21)和式(30)描述了频率域储层岩石中渗流场和电流场之间的耦合关系.
定义流动电位耦合系数KS:当流过岩样的电流密度为0时,岩样两端的反向电位差-ΔU与作用于岩样两端的流体压强差ΔP之比.故由式(30),得
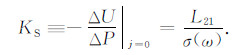
|
(33) |
由式(30)可知,当电流密度j=0,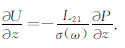
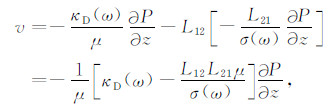
|
(34) |
则有等效动态渗透率或视动态渗透率:
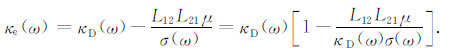
|
(35) |
式(35)中,无量纲参数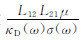
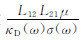
数学模拟储层岩石流动电位的频散特性,需要从具体油田原始岩芯资料中获取一组孔隙度φ、渗透率k,然后确定储层岩石毛管模型的微观参数.在实际计算中,依据文献[24],地层水溶液取NaCl溶液,在地层条件下双电层的阳离子交换量应采用校正公式QV⇒φQV,孔隙度φ的校正公式为φ⇒1-(1-φ)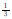
|
|
表 1 流动电位计算基本参数表 Table 1 Basic parameters to calculate the streaming potential |
在孔隙介质中流体流动时,流体黏滞力(作用力)的作用可以改变流体原有运动状态;当流体加速运动时,流体惯性力(反作用力)的作用是维持流体原有运动状态.因此,流体的运动状态就是反作用力(惯性力)与作用力(黏滞力)相互作用的结果.动态渗透率体现了这个相互作用的结果,动态渗透率的虚部和实部的比值,体现了孔隙介质中流体的惯性力与黏滞力的比值,该比值小表示黏滞力占主导地位,该比值大表示惯性力占主导地位.当ReκD[(ω)]=Im κD[(ω)]时,对应的频率称为临界频率.当频率低于临界频率时,黏滞力对孔隙介质中流体的运动起主导作用;当频率高于临界频率时,惯性力对孔隙介质中流体的运动起主导作用.临界频率越大表示孔隙介质中流体的黏滞力占主导作用向惯性力占主导作用的转折点对应的频率越大,反之亦然.
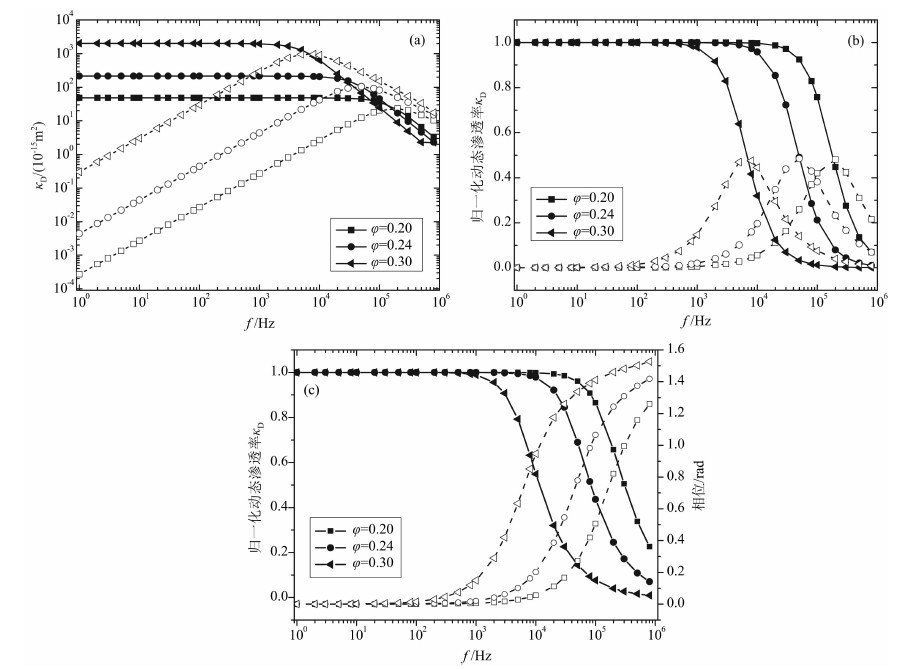
根据上述理论,选取计算参数见表 1,频率范围为1~106 Hz,由式(22)计算动态渗透率的频散关系如图 1a所示,图中模数为孔隙度,动态渗透率的实部由实线表示,虚部由虚线表示.由于动态渗透率的数值随孔隙度变化较大,为了便于比较,动态渗透率的数值被归一化,归一化的动态渗透率的实部和虚部与频率的关系如图 1b所示;归一化的动态渗透率的幅值和相位与频率的变化关系如图 1c所示.由图 1a可以看出,储层孔隙度越大,储层流体的流动能力越大,动态渗透率的幅值越大.由图 1b可以看出,储层孔隙度越大,储层维持流体原有运动状态的能力越大,动态渗透率的临界频率越小,这与文献[25]中所给出的计算结论是一致的.模拟计算还表明:储层岩石的溶液浓度和阳离子交换量对临界频率没有影响,动态渗透率的数值主要与储层孔隙结构和激励源频率及流体性质有关.
|
图 1 动态渗透率的频散特性 (a)原始数值;(b)归一化实部和虚部;(c)归一化幅值和相位. Fig. 1 Frequency dispersion characteristics of the dynamic permeability (a)Original value; (b)Normalized real and imaginary parts; (c)Normalized amplitude and phaseparts. |
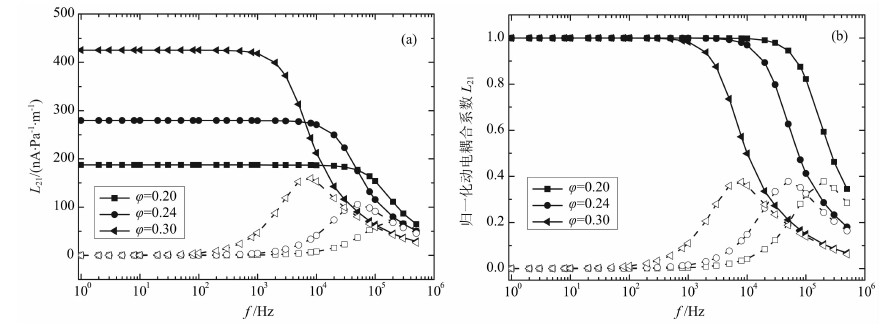
动电耦合系数的大小反映了储层岩石中动电耦合能力的强弱.利用式(31),计算动电耦合系数与频率的关系如图 2a所示,归一化的动电耦合系数与频率的关系如图 2b所示,图中模数为孔隙度,实线表示动电耦合系数的实部,虚线表示动电耦合系数的虚部.储层岩石的微观孔隙结构对流体流动状态有着较大的影响,储层岩石的孔隙度越大,储层流体的流动能力越大,动电耦合系数越大;储层孔隙度越大,储层维持流体原有运动状态的能力越大,动电耦合系数的临界频率越小.
|
图 2 动电耦合系数频散特性与孔隙度的关系 (a)原始数值;(b)归一化值. Fig. 2 Relationship between the frequency dispersion characteristics of the electrokinetic coupling coefficient and theporosity (a)Original value; (b)Normalized value. |
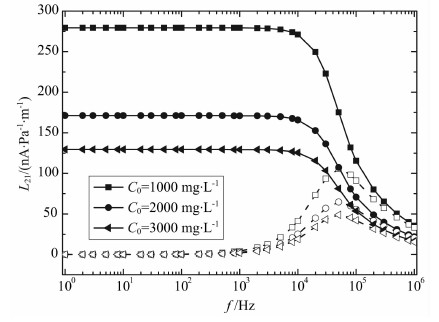
动电耦合系数与溶液浓度的关系,如图 3所示,图中模数为溶液浓度.从图 3可以清晰地看到,溶液浓度越大,孔隙固液界面的双电层作用越弱,流体的动电耦合作用越弱,动电耦合系数越小;溶液浓度对临界频率的影响很小.图 4给出了不同阳离子交换量下动电耦合系数与频率的关系,图中模数为阳离子交换量.阳离子交换量越大,孔隙固液界面的离子吸附能力越强,流体的动电耦合作用越强,动电耦合系数越大;阳离子交换量对临界频率的影响也很小.
|
图 3 动电耦合系数频散特性与溶液浓度的关系 Fig. 3 Relationship between the frequency dispersion characteristics of the electrokinetic coupling coefficient and the concentration |

|
图 4 动电耦合系数频散特性与阳离子交换量的关系 Fig. 4 Relationship between the frequency dispersion characteristics of the electrokinetic coupling coefficient and the cation exchange capacity |
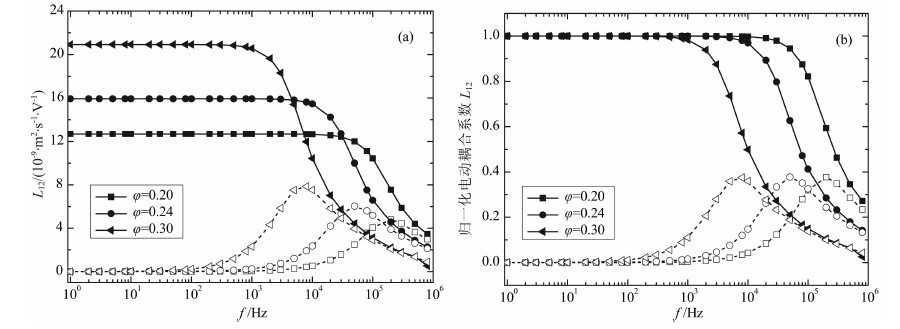
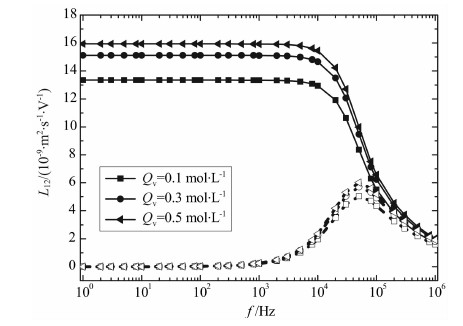
利用式(23)计算电动耦合系数的频散特性,如图 5a所示.图 5a中给出的是三个不同孔隙度下电动耦合系数实部与虚部,图 5b中给出了归一化的电动耦合系数实部与虚部.图中所示孔隙度越大,流体的渗流作用越强,电动耦合系数越大;同时,孔隙度越大,电动耦合系数的临界频率越小.
|
图 5 电动耦合系数频散特性与孔隙度的关系 (a)原始数值;(b)归一化值. Fig. 5 Relationship between the frequency dispersion characteristics of the electroosmosis coupling coefficient and theporosity (a)Original value; (b)Normalized value. |
对比图 2与图 5,动电耦合系数与电动耦合系数实部和虚部的数值并不相同,这是因为描述的物理场不同;但是归一化后,两个耦合系数曲线相互重合,与频率的变化关系完全相同,这说明归一化的动电耦合系数与电动耦合系数满足Onsager互易关系.
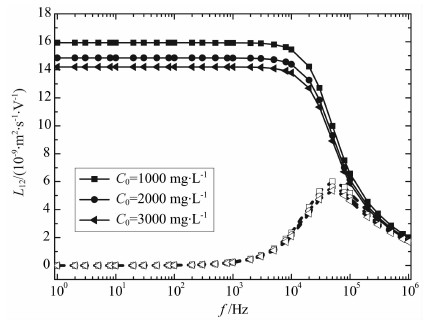
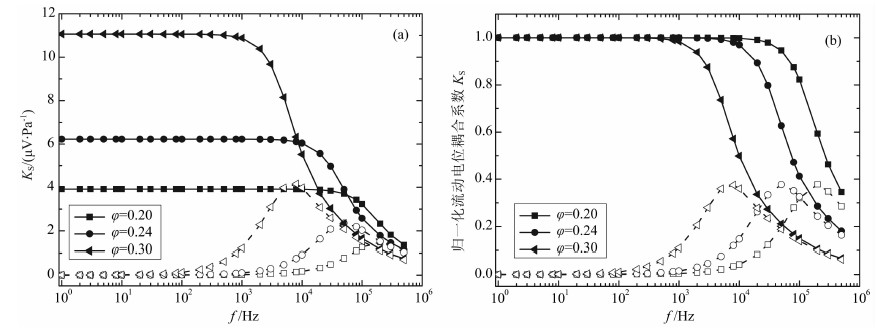
3.2.4 电动耦合系数频散特性与溶液浓度、阳离子交换量的关系溶液浓度对电动耦合系数影响如图 6所示,当溶液浓度增大时,孔隙固液界面的双电层作用减弱,电动耦合系数减小.阳离子交换量对电动耦合系数影响如图 7所示,阳离子交换量越大,孔隙固液界面的离子吸附能力越强,电动耦合系数越大.
|
图 6 电动耦合系数频散特性与浓度的关系 Fig. 6 Relationship between the frequency dispersion characteristics of the electroosmosis coupling coefficient and the concentration |
|
图 7 电动耦合系数频散特性与阳离子交换量的关系 Fig. 7 Relationship between the frequency dispersion characteristics of the electroosmosis coupling coefficient and the cation exchange capacity |
利用式(33),计算流动电位耦合系数的频散特性如图 8a所示;归一化后的流动电位耦合系数如图 8b所示,图中模数为孔隙度.流动电位耦合系数频散特性曲线的变化趋势类似于动电耦合系数的频散特性曲线.孔隙度越大,流体的渗流作用越强,流动电位耦合系数越大;同时,孔隙度越大,流动电位耦合系数的临界频率越小.
|
图 8 流动电位耦合系数频散特性与孔隙度的关系 (a)原始数值;(b)归一化值. Fig. 8 Relationship between the frequency dispersion characteristics of the streaming potential coupling coefficient and the porosity (a)Original value; (b)Normalized value. |
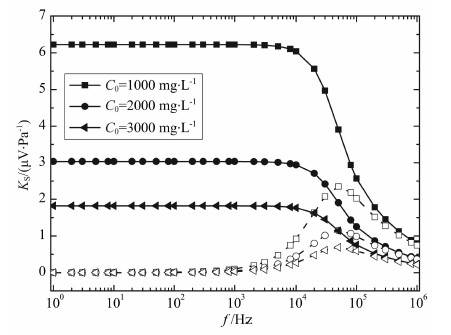
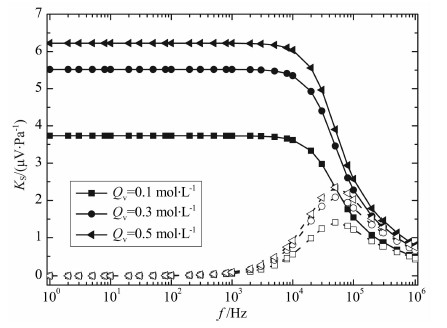
图 9给出了不同溶液浓度下流动电位耦合系数与频率的关系曲线.由图可知,溶液浓度越大,流动电位耦合系数越小.图 10给出了不同阳离子交换量下流动电位耦合系数与频率的关系曲线.由图可知,阳离子交换量越大,流动电位耦合系数越大.
|
图 9 流动电位耦合系数频散特性与浓度的关系 Fig. 9 Relationship between the frequency dispersion characteristics of the streaming potential coupling coefficient and the concentration |
|
图 10 流动电位耦合系数频散特性与阳离子交换量的关系 Fig. 10 Relationship between the frequency dispersion characteristics of the streaming potential coupling coefficient and the cation exchange capacity |
目前流动电位频散特性的研究基础是Pride[11]、Reppert[13]、Yang [15]等建立的理论,这些理论均没有建立起完备的频率域渗流场与电流场相互耦合理论体系,理论表达式中包含了一些物理意义不是很明确的或无法通过实验测得的假定常数,难以定量解释储层岩石流动电位的频散特性.本文利用级数展开双电层电位分布以及贝塞尔函数的方法,导出了频率域电流密度欧姆定律,得到了频率域动态渗透率、电动耦合系数和动电耦合系数的解析表达式,定量模拟了流动电位各耦合系数的频散特性.并得到如下结论:
(1)储层岩石流动电位频散特性是流体惯性力与流体黏滞力相互作用的结果.当频率小于临界频率时,流体黏滞力的作用对流体流动占主导作用,耦合系数的实部变化较小,而虚部近似为零;随着频率增大,流体惯性力的作用逐渐增强,耦合系数的虚部逐渐增大,而实部逐渐减小;当频率高于临界频率,流体惯性力的作用对流体流动占主导作用,耦合系数的实部和虚部逐渐趋于零.
(2)在含水储层岩石中,动态渗透率、动电耦合系数、电动耦合系数和流动电位耦合系数的频散特性受储层岩石结构和电化学因素的影响比较相近.孔隙度越大,储层维持流体原有运动状态的能力越大,各耦合系数的临界频率越小;同时,孔隙度越大,储层流体渗流能力越强,各耦合系数的数值越大.
(3)孔隙固液界面双电层的作用对孔隙流体流动过程影响很小,但对动电耦合效应影响较大.因此,孔隙内溶液浓度和阳离子交换量对动态渗透率无影响,对各耦合系数临界频率的影响也很小.孔隙固液界面双电层的作用大小仅仅影响各耦合系数实部和虚部的数值大小,不影响各耦合系数随频率的变化规律,溶液浓度越大,孔隙固液界面的双电层作用越弱,各耦合系数的数值越小;阳离子交换量越大,孔隙固液界面的双电层作用越强,各耦合系数的数值越大.归一化后,各流动电位耦合系数随频率的变化规律与动态渗透率的变化规律基本一致.
| [1] | Glover P W J, Jackson M D. Borehole electrokinetics. The Leading Edge , 2010, 29(6): 724-728. DOI:10.1190/1.3447786 |
| [2] | Walker E, Glover P W J. Permeability models of porous media:Characteristic length scales, scaling constants and time-dependent electrokinetic coupling. Geophysics , 2010, 75(6): E235-E246. DOI:10.1190/1.3506561 |
| [3] | Glover P W J, Déry N. Streaming potential coupling coefficient of quartz glass bead packs:Dependence on grain diameter, pore size, and pore throat radius. Geophysics , 2010, 75(6): F225-F241. DOI:10.1190/1.3509465 |
| [4] | Tardif E, Glover P W J, Ruel J. Frequency-dependent streaming potential of Ottawa sand. J. Geophys. Res. , 2011, 116(B4): B04206. |
| [5] | 王军, 胡恒山, 杨光, 等. 低频交变压差作用下岩心流动电流和zeta电势实验测量. 地球物理学报 , 2011, 54(8): 2169–2176. Wang J, Hu H S, Yang G, et al. Experimental measurements on streaming current and zeta-potential of core samples under the excitation of low-frequency sinusoidal pressure. Chinese J. Geophys. (in Chinese) , 2011, 54(8): 2169-2176. |
| [6] | Thompson A H, Hornbostel S, Burns J, et al. Field tests of electroseismic hydrocarbon detection. Geophysics , 2007, 72(1): N1-N9. DOI:10.1190/1.2399458 |
| [7] | 关威, 胡恒山, 汤天知, 等. 声电效应测井电声比及其与地层渗透率的关系. 地球物理学报 , 2011, 54(6): 1660–1671. Guan W, Hu H S, Tang T Z, et al. The ratio of the acoustoelectric field to the acoustic pressure in a borehole and its dependence on permeability. Chinese J. Geophys. (in Chinese) , 2011, 54(6): 1660-1671. |
| [8] | 张元中, 肖立志, 楚泽涵, 等. 井孔声电效应转换电磁波的特征. 地球物理学报 , 2005, 48(2): 452–458. Zhang Y Z, Xiao L Z, Chu Z H, et al. The converted electromagnetic wave characteristics of seismoelectric conversion effect in borehole. Chinese J. Geophys. (in Chinese) , 2005, 48(2): 452-458. |
| [9] | Ishido T, Mizutani H. Experimental and theoretical basis of electrokinetic phenomena in rock-water systems and its applications to geophysics. J. Geophys. Res. , 1981, 86(B3): 1763-1775. DOI:10.1029/JB086iB03p01763 |
| [10] | Pride S R, Morgan F D. Electrokinetic dissipation induced by seismic waves. Geophysics , 1991, 56(7): 914-925. DOI:10.1190/1.1443125 |
| [11] | Pride S R. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B. , 1994, 50(21): 15678-15696. DOI:10.1103/PhysRevB.50.15678 |
| [12] | Ken H J, Liu Y C. Electrokinetic flow in a circular capillary with a surface charge layer. J. Colloid Interface Sci. , 1995, 172(1): 222-229. DOI:10.1006/jcis.1995.1246 |
| [13] | Reppert P M, Morgan F D, Lesmes D P, et al. Frequency-dependent streaming potentials. J. Colloid Interface Sci. , 2001, 234(1): 194-203. DOI:10.1006/jcis.2000.7294 |
| [14] | Reppert P M, Morgan F D. Frequency-dependent electroosmosis. J. Colloid Interface Sci. , 2002, 254(2): 372-383. DOI:10.1006/jcis.2002.8596 |
| [15] | Yang J, Grundke K, Bellmann C, et al. Oscillating streaming potential and electro-osmosis of multilayer membranes. J. Phys. Chem. B , 2004, 108(6): 2103-2110. DOI:10.1021/jp0359485 |
| [16] | Kang Y J, Yang C, Huang X Y. AC electroosmosis in microchannels packed with a porous medium. J. Micromech. Microeng. , 2004, 14(8): 1249-1257. DOI:10.1088/0960-1317/14/8/019 |
| [17] | Saunders J H, Jackson M D, Pain C C. A new numerical model of electrokinetic potential response during hydrocarbon recovery. Geophys. Res. Lett. , 2006, 33(15): L15316. DOI:10.1029/2006GL026835 |
| [18] | Revil A, Linde N, Cerepi A, et al. Electrokinetic coupling in unsaturated porous media. J. Colloid Interface Sci. , 2007, 313(1): 315-327. DOI:10.1016/j.jcis.2007.03.037 |
| [19] | Linde N, Jougnot D, Revil A, et al. Streaming current generation in two-phase flow conditions. Geophys. Res. Lett. , 2007, 34(3): L03306. |
| [20] | Jackson M D. Characterization of multiphase electrokinetic coupling using a bundle of capillary tubes model. J.Geophys. Res. , 2008, 113(B4): B04201. |
| [21] | 龚磊, 吴健康, 王蕾, 等. 微通道周期流动电位势及电黏性效应. 应用数学和力学 , 2008, 29(6): 649–656. Gong L, Wu J K, Wang L, et al. Periodical streaming potential and electro-viscous effects in microchannel flow. Applied Mathematics and Mechanics (in Chinese) , 2008, 29(6): 649-656. |
| [22] | 王军, 胡恒山, 徐小蓉, 等. 基于动电效应的岩芯渗透率实验测量. 地球物理学报 , 2010, 53(8): 1953–1960. Wang J, Hu H S, Xu X R, et al. Experimental measurement study on rock permeability based on the electrokinetic effect. Chinese J. Geophys. (in Chinese) , 2010, 53(8): 1953-1960. |
| [23] | Probstein R F.物理化学流体动力学导论.戴干策, 方图南, 范自晖, 译.上海:华东化工学院出版社, 1992. Probstein R F. Physicochemical Hydrodynamics:An Introduction (in Chinese). Dai G C, Fang T N, Fan Z H, Trans. Shanghai:East China Chemical Engineering Institute Press, 1992. |
| [24] | 关继腾, 王谦, 范业活, 等. 利用毛管模型研究泥质砂岩电化学测井响应机理. 地球物理学报 , 2010, 53(1): 214–223. Guan J T, Wang Q, Fan Y H, et al. Study on the mechanisms of electrochemical logging response in shaly sandstone based on capillary model. Chinese J. Geophys. (in Chinese) , 2010, 53(1): 214-223. |
| [25] | 胡恒山, 王克协. 孔隙介质声学理论中的动态渗透率. 地球物理学报 , 2001, 44(1): 135–141. Hu H S, Wang K X. Dynamic permeability in poroelastic medium acoustics. Chinese J. Geophys. (in Chinese) , 2001, 44(1): 135-141. DOI:10.1002/cjg2.v44.1 |
 2013, Vol. 56
2013, Vol. 56

