航空磁测是通过测量空间地磁场,研究地质构造和矿产资源分布的一种航空物探方法.航空磁测包括总场测量、梯度测量等;梯度测量又包括垂向梯度测量、水平梯度测量和全轴(三轴)梯度测量.其中航磁全轴梯度测量利用安装在飞机两翼和尾椎的共四个磁力探头(两翼各一个,尾椎上下各一个),通过计算磁力仪间的地磁场差值获得沿机身方向的纵向水平梯度(纵向梯度)、沿机翼方向的横向水平梯度(横向梯度)和垂直向下的垂向梯度,测量地磁场在空间三个方向的变化率.发展航磁全轴梯度测量与解释方法并将其实用化成为一项进一步提高航空物探对目标物分辨能力的措施[1].在国家高技术研究发展计划(863计划)资助下,中国国土资源航空物探遥感中心成功研制出具有完全自主知识产权的A G S-863航磁全轴梯度勘查系统,关键性指标测试结果表明该系统具有非常好的同步特性、一致性与长期稳定性以及补偿精度[2].通过试验飞行与试生产,共获得了约25000 k m的航磁全轴梯度数据.
根据航磁梯度测量原理,实测航磁梯度数据基本不受日变影响,其中横向梯度反映垂直于测线方向的磁场梯度信息,能够提供测线之间更多的磁场信息[3].基于横向梯度的这一优点,Hardwick[4-5]利用横向梯度与ΔT构建拟测线(pseudo-line),并对相邻的实际测线与拟测线数据进行插值,网格化后的ΔT图突出了测线之间的异常信息、更清晰地反映线性构造或磁性体的走向,可一定程度地减少测线之间的探测盲区.该方法可称为考虑航磁水平梯度变化的ΔT网格化(或简称增强网格化,enhanced gridding).O'Connell等[6]利用横向、纵向梯度也实现了基于最小曲率法[7]的增强网格化.在缺少横向梯度数据的情况下, 对网格化方法的改进[8-13]能够根据原始数据的分布趋势等较合理地接近真实情况, 但不能在数据中增加测线之间的磁场信息. Reford等[14-15]指出由于实测梯度数据存在测线间的水平差, 在增强网格化效果的同时也会增加部分沿测线方向的条带虚假异常, 需要引起注意.本文分别利用理论模型数据、航磁全轴梯度勘查系统试验飞行数据构建拟测线, 结合Akima插值法[16]以及双方向测线型网格化方法, 实现了考虑航磁水平梯度变化的ΔT网格化; 针对Reford指出的条带虚假异常, 采取了对增强后的网格数据去除条带的滤波方法, 有效减少了虚假异常的影响.
2 方法原理 2.1 水平梯度测量原理自主研发的航磁全轴梯度勘查系统可同时获得三个方向的梯度数据.其中, 横向梯度测量利用安装在飞机两翼的两个磁力探头获得地磁场沿机翼方向的变化率.横向梯度可表示为[3]
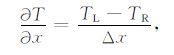
|
(1) |
其中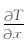
航磁测量仪器的采样率一般为每秒10次或更高,航磁的测点间距远小于测线间距.因此,航磁数据是一种典型的测线型数据,适于利用测线型网格化方法进行网格化[17-18].测线型网格化可分为双方向、单方向网格化.双方向是指对测线数据先沿某一方向进行插值,再沿垂直于前一插值方向进行插值;单方向是指仅沿某一方向进行插值,最终获得网格化数据.Hardwick增强网格化属于测线型网格化,这里我们仅讨论Hardwick方法,并在其理论基础上使用Akima插值以及双方向测线型网格化方法进行考虑航磁水平梯度变化的ΔT网格化研究.
Hardwick利用横向梯度数据构建拟测线,拟测线的ΔT值可表示为[4]
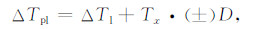
|
(2) |
其中ΔTpl表示拟测线上的ΔT,ΔTl为实际测线上的ΔT,Tx为横向梯度,D为拟测线与实际测线的间距,式中±符号表示利用每条实际测线的ΔT和横向梯度能够构建两条拟测线,位于实际测线两侧.构建拟测线后的测线数为原始测线数的3倍.在构建拟测线的基础上,将所有测线进行测线型网格化,插值方法可采用Akima方法.该插值方法中将过点Pi(xi)和Pi+1(xi+1)的三次多项式设为
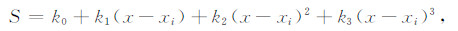
|
(3) |
其中,k0=y1,k1=t1,k2=[3(S2-S1)/(xi+1-xi)-2t1-t2]/(xi+1 -xi),k3=[t1 +t2-2(S2-S1)/(xi+1-xi)]/(xi+1 -xi),S1、S2分别为点Pi、Pi+1上的函数值,t1、t2分别为点Pi、Pi+1上的斜率。每个点的斜率t由附近5个点(依次为P 1、P 2、P3、P4和P5)确定,点P3的斜率为
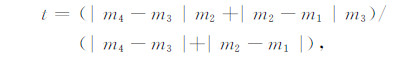
|
(4) |
其中m1、m2、m3和m4分别为线段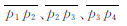
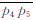
为了实现增强网格化,我们沿测线方向分别对每条测线数据进行插值,再沿垂直于测线方向进行插值,步骤如下:
(1)沿测线方向分别对ΔT和横向梯度进行Akima插值.航空磁测以固定的测线间距进行飞行测量,由于气流等影响,实际飞行轨迹为折线.需要指出,Akima插值法仅针对所有插值点的坐标连线为直线的情况,为了使其适用于折线,在计算式(3)及斜率时,以下式代替xi+1 -xi:
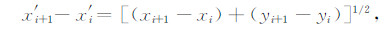
|
(5) |
其中(xi,yi)、(xi+1,yi+1)为测量点的平面坐标.为了保证插值精度,假设X轴沿测线方向,同样需要对Y坐标值进行插值;
(2)通过式(2)计算拟测线上的ΔT.拟测线的作用是提供测线之间的磁场变化趋势,因此D并不一定等于二分之一探头间距,D的取值范围通常大于零,小于二分之一测线间距;
(3)沿垂直于测线方向对实际测线和拟测线数据进行Akima插值.
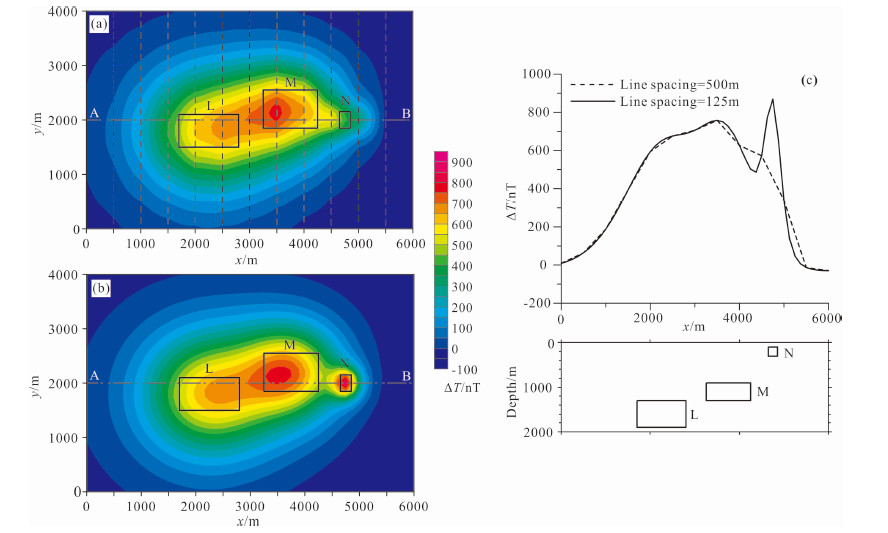
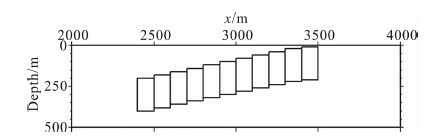
3 模型数据试验 3.1 试验一在试验一中,我们设计了三个垂直磁化的矩形体,模型参数见表 1,平面和剖面位置分别见图 1a和图 1c,测线高度为200 m.在图 1a中,L、M模型分别横跨两条测线(测线间距为500 m,本文中所有网格数据的间距均为125 m),磁异常十分明显;N模型恰好在两条测线之间,磁异常不明显.当加密测线至125 m间距后,N模型的磁异常清晰可见(图 1b、图 1c),说明当测线间距较大时,减弱了对测线之间磁异常的反映.
|
|
表 1 模型参数 Table 1 Parameter of the model |
|
图 1 模型位置及ΔT (a)ΔT,测线间距500 m;(b)ΔT,测线间距125 m;(c)ΔT剖面(图 1a和图 1 b的A-B剖面). Fig. 1 Model location and total field (a)Total field, line spacing:500 m.(b)Total field, line spacing:125 m.(c)Total field profile(A-B profile in Fig. 1a and Fig. 1 b). |
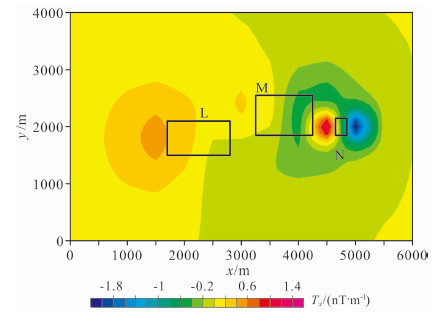
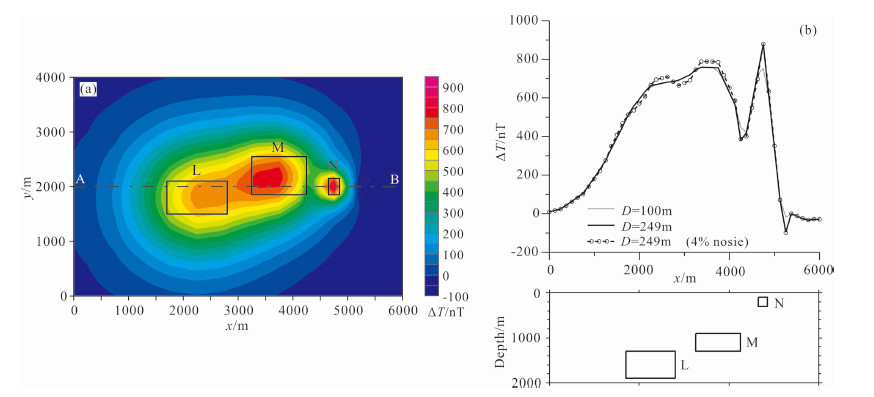
图 2为500 m测线间距的横向梯度(Tx),三个模型的梯度异常一正一负分布在模型体中心两侧,由于N模型顶面埋深较小,梯度数据更突出对N模型的反映.在既定的测线间距下,由于横向梯度能够反映测线之间更多的磁场信息,可利用这部分信息进行网格化.我们利用图 1a和图 2的数据进行增强网格化.增强网格化后的ΔT(图 3a)可明显反映N模型,在原始数据中加入4 %随机噪声的增强网格化也同样能够反映N模型(图 3 b).由于L、M模型横跨了两条测线,其增强网格化效果不明显.我们对式(2)中的D选取了不同的值,可看到D=249 m比D=100 m的曲线异常幅值大(图 3 b),增强效果更明显.
|
图 2 横向梯度(测线间距500 m) Fig. 2 Transverse horizontal gradient(line spacing:500 m) |
|
图 3 增强网格化结果(测线间距500 m) (a)ΔT平面,数据无噪声,D=249 m;(b)ΔT剖面(图 3a的A-B剖面). Fig. 3 Enhanced total field(line spacing:500 m) (a)Total field, without noise andD=249 m; (b)Total field profile(A-B profile in Fig. 3a). |
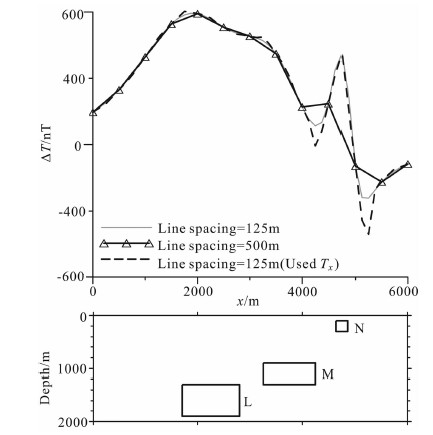
依照表 1中的模型参数,分析斜磁化情况,以倾角60°(磁化方向与X轴正方向夹角)为例,对测线间距为500 m的数据进行增强网格化处理.网格化A-B剖面结果见图 4,测线间距为500 m的剖面异常对N模型的反映不明显,但测线间距为125 m的剖面异常对N模型反映明显;将增强网格化结果(D=240 m)与125 m测线间距的异常进行对比,两者正异常吻合较好,负异常趋势被加强.
|
图 4 斜磁化异常的增强网格化结果(D=240 m) Fig. 4 Enhanced gridding of oblique m ag netization ano m aly(D=240 m) |
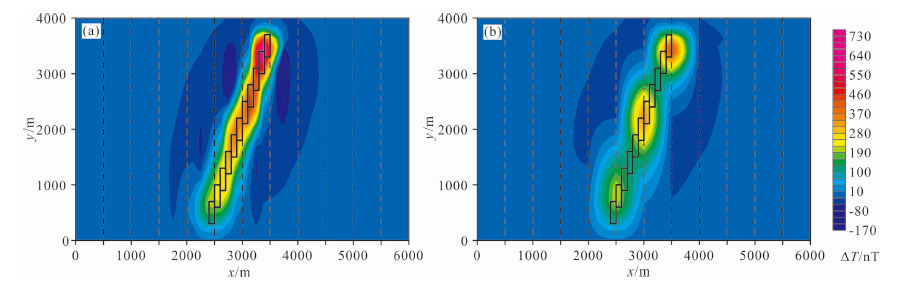
在试验二中,我们设计了垂直磁化的11个矩形体,磁化强度都为10 A/m,剖面和平面位置见图 5、图 6,测线间距为500 m,测线高度为200 m.每个模型的顶面埋深不同,组成了具有一定走向的整体(图 6).增强后的ΔT(图 6a)对模型的整体走向反映得更明显、更连续,减少了原始ΔT(图 6 b)的“串珠状”现象.测线方向通常垂直或基本垂直于测区内的主要构造,但当有部分构造的走向与测线方向相近时,利用增强网格化可以一定程度地增强对这部分构造的反映.
|
图 5 模型剖面 Fig. 5 Model profile |
|
图 6 已增强网格化(a)和未增强网格化(b)ΔT(D=249 m) Fig. 6 Total field after en hancing(a)and before en hancing(b)(D=249 m) |
我们选取了2011年A G S-863航磁全轴梯度勘查系统在河北某地的部分试验飞行数据进行增强网格化处理,数据未化极,已经过水平调整(leveling)[19].试验飞行的测线间距为250 m,平均飞行高度为200 m.为了验证增强网格化的效果,我们对原始测线进行抽稀,每两条测线抽取一条,抽稀后的测线间距为500 m.利用抽稀后的数据进行增强网格化处理,处理结果与抽稀前的网格化图进行对比,以此来评价增强网格化效果.
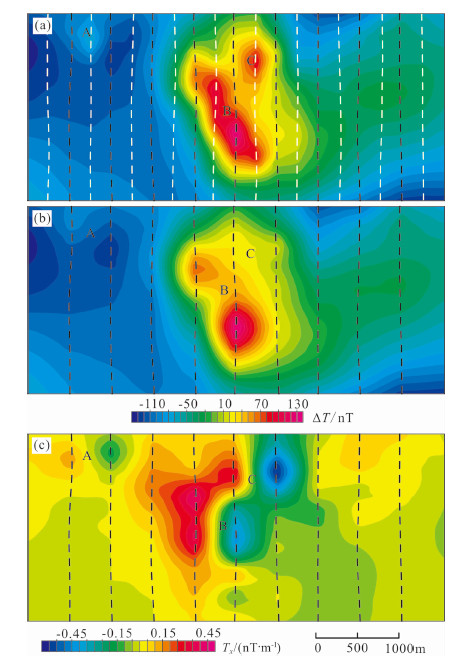
图 7a为测线抽稀前的ΔT,图中黑色和白色虚线分别为保留和去除的测线.可看到图中有三个较明显的磁异常,A、C异常分布在两黑色虚线之间,B异常横跨了两条黑色虚线,具有一定走向.测线抽稀后(图 7 b),异常的面貌发生了变化,A、C异常已不明显,B异常的连续性被削弱.测线抽稀后的横向梯度(图 7c)仍然能够反映三个异常,呈现一正一负的梯度特征.
|
图 7 测线抽稀前后的ΔT与横向梯度 (a)ΔT,测线间距250 m;(b)ΔT,测线间距500 m;(c)横向梯度,测线间距500 m. Fig. 7 Total field before and after rarefying and transverse horizontal gradient (a)Total field, line spacing:250 m.(b)Total field, line spacing:500 m.(c)Transverse horizontal gradient, line spacing:500 m. |
我们利用图 7 b和图 7c的数据进行增强网格化处理.增强网格化后(图 8a),A、C异常已被增强,B异常的连续性也被较好地恢复,但在异常平缓区域出现了线性虚假异常(图 8 a的红色圈内).Reford等[14]指出由于实测梯度存在测线间的水平差,在增强网格化的同时会增加部分沿测线方向的条带虚假异常,需要对梯度数据进行调平处理,但调平后会残留少部分水平差,增强网格化结果仍然会存在条带虚假异常.我们针对增强后的结果进行去条带处理.去除条带的方法[20-22]较多,由于这些虚假异常是在增强网格化过程中增加的,为了不损失原有的地质信息,我们将图 8a与图 7 b相减,其差值为增强网格化所增加的信息,其中包括条带虚假异常.选用方向滤波对差值进行滤波处理,滤波器为余弦方向滤波:
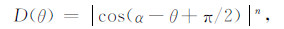
|
(6) |
其中α是压制条带的方向,n是滤波阶数,θ=arctan(u/v),u、v是频率域波数.因为要压制南北向条带,故α=0;n选择0.3.将滤波后的结果与图 7 b相加即为最后的增强网格化结果(图 8 b),原有的条带虚假异常被滤掉,三个异常的增强效果依然明显.
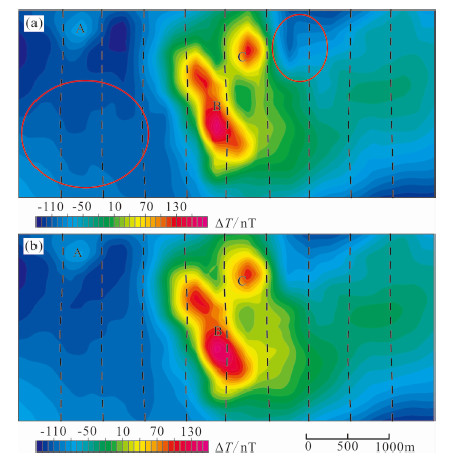
|
图 8 滤波前(a)和滤波后(b)的增强网格化结果(D=240 m) Fig. 8 Enhanced gridding results(D=240 m) (a)before filtering and(b)after filtering |
本文利用航磁横向梯度与ΔT数据构建拟测线,结合Akima插值以及双方向测线型网格化方法实现了考虑航磁水平梯度变化的ΔT网格化,并针对网格化结果中的虚假异常采取了解决方法,网格化方法及取得的认识对开展航磁梯度测量具有实际意义.
综合首次考虑航磁水平梯度变化的ΔT网格化方法研究,我们得出下面结论:
(1)模型数据与实际数据处理表明,增强网格化可利用梯度信息,突出测线之间的异常、更清晰地反映构造或磁性体走向,提高了网格化图的分辨率;
(2)由于实测梯度数据存在测线间的水平差,增强网格化结果会存在沿测线方向的条带虚假异常,可采用方向滤波对增强前、后网格数据的差值进行去除条带处理;
(3)对于横跨多条测线或走向与测线近似垂直的异常,或在原始测线已较好反映的异常,增强网格化效果不明显.此外,由于机翼的磁力探头仅偏离测线十多米,其仅能测得有限的测线之间的信息,增强网格化效果会随着测线间距的增大而减弱;
(4)增强网格化图可作为中、大比例尺(测量比例尺大于1:5万)原始ΔT网格化图的补充,有助于航磁数据的解释.梯度数据除了存在调平后残留的水平差,也会存在残留的随机噪声,要注意这部分噪声对增强网格化结果的影响.
网格化结果中的条带虚假异常影响了网格化效果,建议对梯度和总场数据进行更有效的调平,此外可对网格化结果进行微调平以及采用其他更有效的滤波方法.
致谢研究工作得到了中国国土资源航空物探遥感中心许多同事的支持与帮助,在此表示衷心感谢.同时感谢两位匿名审稿专家提出宝贵建议.
| [1] | 熊盛青. 我国航空重磁勘探技术现状与发展趋势. 地球物理学进展 , 2009, 24(1): 113–117. Xiong S Q. The present situation and development of airborne gravity and magnetic survey techniques in China. Progress in Geophys. (in Chinese) , 2009, 24(1): 113-117. |
| [2] | 骆遥, 段树岭, 王金龙, 等. AGS-863航磁全轴梯度勘查系统关键性指标测试. 物探与化探 , 2011, 35(5): 620–625. Luo Y, Duan S L, Wang J L, et al. Key indicators testing for AGS-863 three axis airborne magnetic gradiometer. Geophysical & Geochemical Exploration (in Chinese) , 2011, 35(5): 620-625. |
| [3] | Cowan D R, Baigent M, Cowan S. Aeromagnetic gradiometers-a perspective. Exploration Geophysics , 1995, 26(3): 241-246. DOI:10.1071/EG995241 |
| [4] | Hardwick C D. Gradient-enhanced total field gridding.//69th Annual International Meeting:SEG Expanded Abstracts, 1999, 18:381-384. http://www.oalib.com/references/19002106 |
| [5] | Hardwick C D. Two methods of gradient-enhanced gridding-A discussion. 2004 SEG Expanded Abstracts, Workshop on Magnetic Gradiometry, 2004. http://www.oalib.com/references/19002107 |
| [6] | O'Connell M D, Smith R S, Vallee M A. Gridding aeromagnetic data using longitudinal and transverse horizontal gradients with the minimum curvature operator. The Leading Edge , 2005, 24(2): 142-145. DOI:10.1190/1.1876036 |
| [7] | Briggs I C. Machine contouring using minimum curvature. Geophysics , 1974, 39(1): 39-48. DOI:10.1190/1.1440410 |
| [8] | 王万银, 邱之云. 一种稳定的位场数据最小曲率网格化方法研究. 地球物理学进展 , 2011, 26(6): 2003–2010. Wang W Y, Qiu Z Y. The research to a stable minimum curvature gridding method in potential data processing. Progress in Geophys (in Chinese) , 2011, 26(6): 2003-2010. |
| [9] | 郭良辉, 孟小红, 郭志宏. 位场数据网格化的反插值法. 地球物理学报 , 2006, 49(4): 1183–1190. Guo L H, Meng X H, Guo Z H. Inverse interpolation for gridding of potential field data. Chinese J. Geophys (in Chinese) , 2006, 49(4): 1183-1190. |
| [10] | 郭良辉, 孟小红, 郭志宏, 等. 反插值法实现地球物理数据快速网格化. 地球物理学进展 , 2005, 20(3): 671–676. Guo L H, Meng X H, Guo Z H, et al. Fast gridding of geophysical data with inverse interpolation. Progress in Geophys (in Chinese) , 2005, 20(3): 671-676. |
| [11] | Smith R S, O'Connell M D. Interpolation and gridding of aliased geophysical data using constrained anisotropic diffusion to enhance trends. Geophysics , 2005, 70(5): 121-127. DOI:10.1190/1.2080759 |
| [12] | Bhattacharyya B K. Bicubic spline interpolation as a method for treatment of potential field data. Geophysics , 1969, 34(3): 402-423. DOI:10.1190/1.1440019 |
| [13] | Smith R S, O'Connell M D. An improved method for trending of features on aeromagnetic maps. Proceedings of Exploration 07:Fifth Decennial International Conference on Mineral Exploration, 2007:853-861. http://www.oalib.com/references/19002112 |
| [14] | Reford S. Gradient enhancement of the total magnetic field. The Leading Edge , 2006, 25(1): 59-66. DOI:10.1190/1.2164757 |
| [15] | Reford S. Gradient enhancement of the total magnetic field. SEG International Exposition and 74th Annual Meeting, 2004. http://www.oalib.com/references/19002120 |
| [16] | Akima H. A new method of interpolation and smooth curve fitting based on local procedures. Journal of the Association for Computing Machinery , 1970, 17(4): 589-602. DOI:10.1145/321607.321609 |
| [17] | 郭志宏. 一种实用的等值线型数据网格化方法. 物探与化探 , 2001, 25(3): 203–208. Guo Z H. A practical contour type data gridding technique. Geophysical & Geochemical Exploration (in Chinese) , 2001, 25(3): 203-208. |
| [18] | 郭志宏.双三次样条内插网格化方法软件的研制开发及应用.//熊盛青, 唐文周, 姚正煦.航空物探遥感论文集.北京:地质出版社, 1999:27-33. Guo Z H. The development and application of the software of the double cubic spline interpolated gridding technique.//Xiong S Q, Tang W Z, Yao Z X, eds. Papers of Aero Geophysical Survey and Remote Sensing (in Chinese). Beijing:Geological Publishing House, 1999:27-33. |
| [19] | Luyendyk A P J. Processing of airborne magnetic data. AGSO Journal of Australian Geology and Geophysics , 1997, 17(2): 31-38. |
| [20] | Minty B R S. Simple micro-levelling for aeromagnetic data. Exploration Geophysics , 1991, 22(4): 591-592. DOI:10.1071/EG991591 |
| [21] | Fedi M, Florio G. Decorrugation and removal of directional trends of magnetic fields by the wavelet transform:Application to archaeological areas. Geophysical Prospecting , 2003, 51(4): 261-272. DOI:10.1046/j.1365-2478.2003.00373.x |
| [22] | Pilkington M, Roest W R. Removing varying directional trends in aeromagnetic data. Geophysics , 1998, 63(2): 446-453. DOI:10.1190/1.1444345 |
 2013, Vol. 56
2013, Vol. 56

