2. 大连理工大学海岸和近海工程国家重点实验室, 大连 116024;
3. 郑州大学水利与环境学院, 郑州 450001
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China;
3. College of Water Conservancy & Environmental Engineering, Zhengzhou University, Zhengzhou 450001, China
近年来,探地雷达(GPR)作为一种快速、高分辨率、无破损的检测手段,已经广泛应用于浅地层目标探测中.通过分析实测雷达数据,可以获得地层分界面以及地下埋藏目标的位置等信息.正演数值模拟是研究探地雷达电磁波在地下结构中传播规律的有效手段,也是解释探地雷达实测数据的重要依据.
目前,探地雷达电磁波数值模拟方法主要包括,射线追踪法[1],傅里叶方法[2],积分方程法[3],时域有限差分(FDTD)法[4-7],ADI-FDTD[8]方法等.但这些方法在效率和精度等方面总存在一些问题.比如FDTD方法的计算效率受到CFL稳定条件的约束,ADI-FDTD方法虽然摆脱了CFL稳定条件的约束,但较大的时间步长会增加数值色散性.
辛算法是一种保持Hamilton系统相空间体积不变的算法,在计算过程中不会引入人为的耗散机制和虚假的激励,在有关结构整体性、稳定性以及长期模拟计算方面,具有显著优势,已经被应用于地震波、声波的正演计算中[9-10].虽然由于地下材料损耗性的存在,电磁波在地下结构中的传播问题不能看作经典Hamilton系统,但幸运的是,辛算法依然可以应用.辛分块龙格库塔(SPRK)方法是应用较为广泛的一类时域辛算法,对于二维问题,该方法的一个显著优点是它仅需要两个方程就可以完整的描述整个电磁场,而FDTD方法需要三个方程,这可以极大的减少电脑内存的占用率和计算时间.本文采用一阶Radau IA-IA辛格式,主要基于两点原因:(1)对于电磁波在有耗介质中的传播问题,它是显式的;(2)在众多辛算法中,它的计算量是最少的[11].
本文首次应用一阶Radau IA-IA辛分块龙格库塔方法模拟探地雷达电磁波在复杂地下结构中的传播,吸收边界采用二阶透射边界条件.通过数值算例验证了本文算法的精度和效率.并基于本文算法模拟合成两种复杂地电结构的GPR探测wiggle图,这对于正确解释实测雷达数据是有益的.
2 原理 2.1 Hamilton系统和辛分块龙格库塔方法[12-13]Hamilton系统对偶方程可以表示为
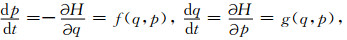
|
(1) |
其中,H代表Hamilton函数.如果Hamilton函数可以表示为如下可分离形式
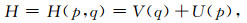
|
(2) |
则对偶方程可化为
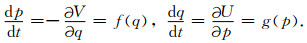
|
(3) |
一个s步分块龙格库塔方法可以用两个Butecher表给出:
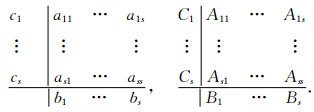
|
(4) |
将式(4)代入式(3)可以得到如下关系式[14]:
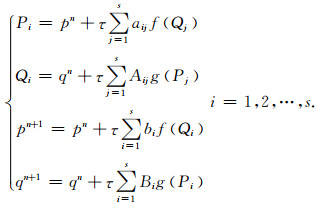
|
(5) |
如果式(4)的系数满足
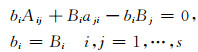
|
(6) |
那么该分块龙格库塔方法是辛的.
一阶Radau IA-IA辛分块龙格库塔方法的Butecher表示如下:
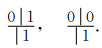
|
(7) |
各向同性有耗介质中,Maxwell方程组表示为
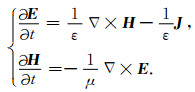
|
(8) |
其中,E表示电场向量,H表示磁场向量,电流密度J=σE,ε,μ,σ分别表示介电常数、磁导率和电导率.
引入矢量磁位H=×∇A并令E=-Y,则有耗介质中的广义Hamilton函数可以表示为[15]
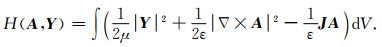
|
(9) |
根据式(1),Maxwell方程组可化为
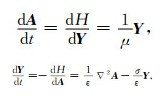
|
(10) |
对于二维TM波,方程(10)可以改写为
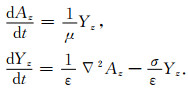
|
(11) |
其中,Az和Yz分别表示场组分A和Y在z方向的分量.
电场Ez,磁场Hx和Hy可以由下式得到
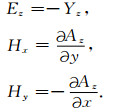
|
(12) |
为了简化起见,下文中省略下标z.
2.3 Maxwell方程组的离散FDTD方法采用Yee网格离散Maxwell旋度方程组中的时间和空间偏微分算子,即电场和磁场在空间上和时间上彼此间隔半个空间步长和时间步长.但是,在辛分块龙格库塔方法中,电场和磁场的离散值是被定义在同一空间网格节点和相同的时间步上.
采用中心差分近似拉普拉斯算子,并设Δx=Δy=Δs,则
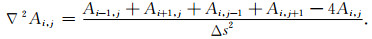
|
(13) |
将(7)式应用到(11)式,并带入式(13),可得如下一阶辛分块龙格库塔方法迭代格式:
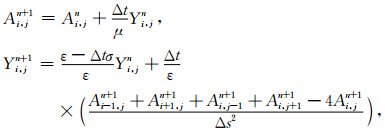
|
(14) |
其中,Ai,jn和Yi,jn分别表示场组分A和Y在nΔt时刻节点(i,j)处的离散值.
3 边界条件探地雷达电磁波在地下结构中的传播是开域问题,但由于受到计算机内存的限制,辛分块龙格库塔方法只能在有限区域内进行.因此,在截断边界处需要设置吸收边界条件.透射边界是由无限域模型导出的一类具有普遍适用性的局部吸收边界条件,具有易于计算机实现,精度可控等优点,已经广泛应用于各类工程波动问题中.N阶多次透射公式(MTF)可以表示为[16-17]
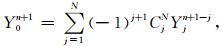
|
(15) |
式中Cjm=m!/(m-j)!/j!,Yjn表示nΔt时刻空间点-jcaΔt处的离散值,ca表示人工波速.本文中采用二阶透射边界,则式(15)可以简化为
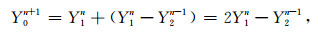
|
(16) |
MTF中,计算点x=-jcaΔt一般和空间网格节点x=-jΔx不重合,故Yjn需要用空间网格节点的离散值内插计算.如图 1所示,以右截断边界上一点为例,二阶MTF中的Y1n和Y2n-1可按以下差值公式求得
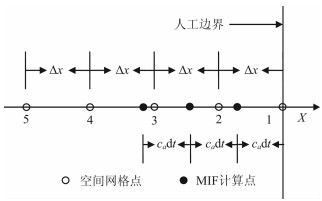
|
图 1 右边界处MTF计算点与空间网格节点示意图 Fig. 1 Arrangement of the computational points and the spatial mesh points on the right artificial boundary |
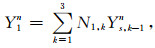
|
(17) |
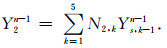
|
(18) |
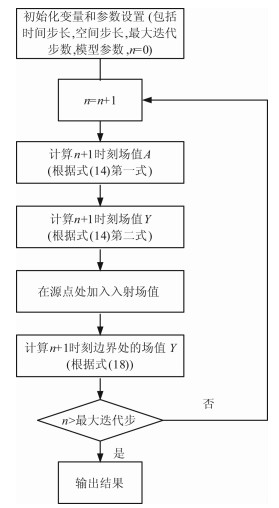
式中Ys,jn表示nΔt时刻空间网格节点-jΔx处的离散值.N1,1=(2-s)(1-s)/2,N1,2=s(2-s),N1,3=s(s-1)/2,s=caΔt/Δx,N2,1=N1,12,N2,2=2N1,1N1,2,N2,3=2N1,1N1,3+N1,22,N2,4=2N1,2N1,3,N2,5=N1,32.文中ca取电磁波在边界处介质中的传播速度.类似的,可以得到其它边界点的离散格式.图 2给出了采用SPRK方法进行数值模拟的流程图.
|
图 2 SPRK方法流程图 Fig. 2 The flowchart of the SPRK method |
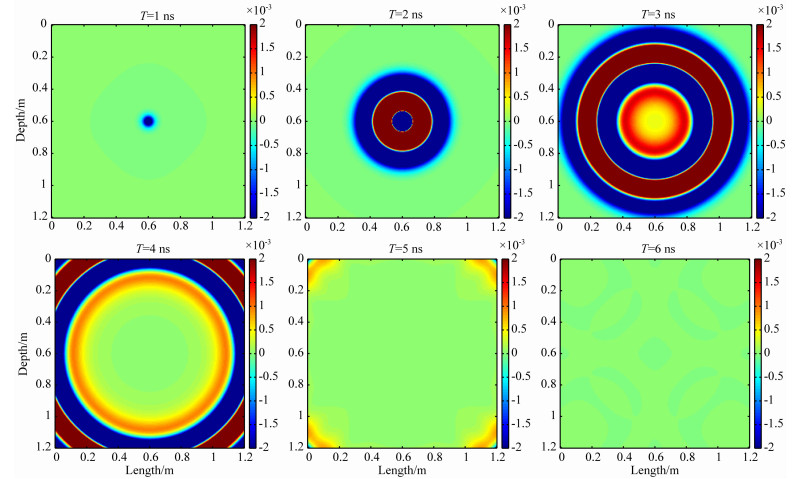
为了验证二阶透射边界的吸收效果,建立一个二维空间模型,模拟区域为1.2m×1.2m的正方形,内部充满空气,在模拟区域的中心位置加入一个Ricker子波.时间步长选取0.01ns,空间步长选取0.5cm.图 3为不同时刻场组分Yz的分布示意图,由图 3可以看出,二阶透射边界的吸收效果令人满意.
|
图 3 不同时间步场组分Yz分布图 Fig. 3 Distribution of field component Yz at different times teps |
和FDTD方法一样,为保证辛算法的计算稳定性,空间间隔和时间步长的选取也需要满足稳定性条件.本文采用增长矩阵方法对辛算法的数值稳定性进行分析.为简化起见,假设材料都是无损耗的,则方程(14)可以重写为
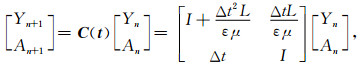
|
(19) |
式中C(t)为增长矩阵.L为将二维平面波解
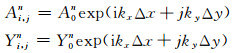
|
(20) |
带入拉普拉斯算符化简后得到的离散格式:
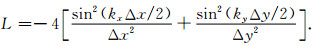
|
(21) |
可证明当|C(t)|≤1的所有特征值的绝对值≤1时,该辛算法是稳定的[17].因此,令Δx=Δy=δ,可以得到一阶辛算法的二维稳定条件为
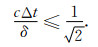
|
(22) |
式中c表示光速.由(22)式可知,对于二维情况,辛算法的稳定条件和FDTD方法相同.
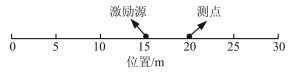
5 数值算例 5.1 模型1首先,通过电磁波在一维自由空间中的传播问题来验证本文算法的精度和效率.如图 4所示,在点x=15m处加入高斯脉冲(式(23)),空间间隔和时间步分别取0.1m和0.2ns,计算步设置为500步.
|
图 4 一维计算模型示意图 Fig. 4 The schematic diagram of 1-D model |
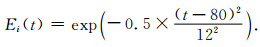
|
(23) |
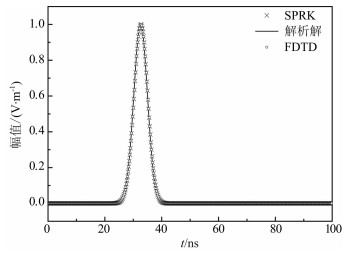
图 5给出了x=20m处SPRK方法,FDTD方法和解析方法得到的场值结果.图 6进一步给出了两种方法和解析解的误差对比.
|
图 5 x=20处场组分E随时间变化图 Fig. 5 The time history of field component E at x=20 |

|
图 6 场组分E计算误差随时间变化关系图 Fig. 6 The absolute error of field component E at different time step |
从图 5和图 6中可以看出,本文算法可以和FDTD方法达到同样的计算精度,但是整个计算过程FDTD需要耗费0.072862s,而SPRK方法仅需要耗费0.0546465s,节省了大约25%的计算时间.因此,本文算法的计算效率明显优于FDTD方法.
5.2 模型2由于地下层状结构交界面不一定是平面,本例设计了一个起伏交界面地下模型并对该模型GPR探测wiggle图进行二维正演模拟.该地下模型由三层介质组成,第二层和第三层介质的交界面为曲面,并且在第一层和第二层介质的交界面处存在一个2m×2m的正方形空洞.具体模型尺寸和材料介电参数选取如图 7所示.时间步长、空间间隔分别选取0.1ns和0.05m.对于二维问题,激励源可以看作是固定在发射天线处的线源,入射波形采用单位波幅的Ricker子波,中心频率选取100MHz(图 8).
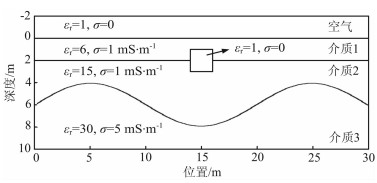
|
图 7 含有起伏交界面地下模型示意图 Fig. 7 The schematic diagram of subsurface model with curve interface |
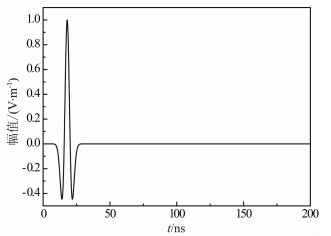
|
图 8 中心频率为100MHz的单位波幅Ricker子波波形图 Fig. 8 A Ricker waveform of unity amplitude and central frequency of 100 MHz |
本例中,采用分离天线进行探地雷达电磁波的激发和接收,发射天线和接收天线之间距离为1m.从x=0m出发,每0.2m激发和接收一次,从而获得合成的地下结构模拟GPR探测wiggle图(图 9).

|
图 9 含有起伏交界面地下模型wiggle图 Fig. 9 The wiggle map of subsurface model with curve interface |
由模拟的wiggle图可以看出,地下结构的分界面显示清晰,来自起伏交界面的反射波在图上显示为一条与地下起伏界面相同走势的同相轴.在脱空处存在明显的呈双曲型的绕射波,同相轴出现不连续现象.本例中模拟得到GPR探测wiggle图的时间,FDTD算法需1.7673h,而本文算法仅需要1.4137h.
5.3 模型3土基不密实是一种常见的工程质量问题,本例建立一个局部不密实的地下模型,并模拟合成GPR探测wiggle图.如图 10所示,该地下模型由两层介质组成,在交界面上有一倾斜不密实区域,另外在第一层介质内还存在一根直径为1m的圆形水管.假设不密实区域孔隙率为10%,并且空隙中充满水,那么不密实区域的介电常数选取可以采用随机分布的方法,即该区域相对介电常数在水的相对介电常数和第二层介质的相对介电常数之间随机分布.其中,相对介电常数为水的节点占总数的10%.时间步长,空间步长以及天线的选取同例5.2节.图 11给出了模拟合成的含有不密实区域地下模型GPR探测wiggle图.由图 11可以看出,不密实区域上部倾斜边界在图上显示清晰,水管处出现明显的双曲型的绕射波.在不密实区域及其下部出现大量无规则的绕射波和反射波,这主要是由于该区域中水的介电常数是随机设置的,电磁波在传播到这些介电常数不一样的点时都会产生反射和绕射,从而生成大量的杂乱无规则的绕射波和反射波.计算得到图 11,FDTD方法需要1.7595h,而本文算法仅需要1.4098h.
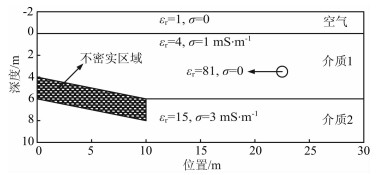
|
图 10 存在不密实区域地下模型示意图 Fig. 10 The schematic diagram of subsurface model with less dense |

|
图 11 含有不密实区域地下模型wiggle Fig. 11 The wiggle map of subsurface model with less dense |
通过以上两例可以看出,通过本文算法模拟得到的地下结构GPR探测wiggle图不仅可以较为准确的反映地下结构的主要特征,而且可以显著的节省计算时间.这为解释实际探地雷达检测数据提供了重要依据.
6 结论本文结合一阶显式辛分块龙格库塔方法与二阶透射边界条件模拟探地雷达电磁波在复杂地下结构中的传播.通过对比本文算法与时域有限差分法计算结果可以看出,两种算法的计算结果吻合非常好,但本文方法的计算时间仅为时域有限差分法的75%,因此,本文算法的计算效率要优于时域有限差分法.另外,基于本文算法模拟合成了含有脱空、起伏交界面、水管、不密实区域的复杂地电模型GPR探测wiggle图有益于解释实测雷达数据.
本文工作主要集中于电磁波在层状有耗介质中的传播问题,但辛算法的应用并不局限于此,对于频散介质、各向异性介质,也能取得比较好的结果.
| [1] | 邓世坤, 王惠濂. 探地雷达图像的正演合成与偏移处理. 地球物理学报 , 1993, 36(4): 528–536. Deng S Q, Wang H L. The forward synthesizing and migration processing for GPR image. Acta Geophysica Sinica (Chinese J. Geophys.) (in Chinese) , 1993, 36(4): 528-536. |
| [2] | 钟燕辉, 张蓓, 王复明. 多层介质中路面雷达电磁波传播数值模拟. 大连理工大学学报 , 2006, 46(5): 726–729. Zhong Y H, Zhang B, Wang F M. Numerical simulation of ground penetrating radar wave propagation in multi-layered medium. Journal of Dalian University of Technology (in Chinese) , 2006, 46(5): 726-729. |
| [3] | Simsek E, Liu J G, Liu Q H. A spectral integral method and hybrid SIM/FEM for layered media. IEEE Transactions on Microwave Theory and Techniques , 2006, 54(11): 3878-3884. DOI:10.1109/TMTT.2006.883647 |
| [4] | Irving J, Knight R. Numerical modeling of ground-penetrating radar in 2-D using MATLAB. Computers & Geosciences , 2006, 32(9): 1247-1258. |
| [5] | 卢成明, 秦臻, 朱海龙, 等. 探地雷达检测公路结构层隐含裂缝实用方法研究. 地球物理学报 , 2007, 50(5): 1558–1568. Lu C M, Qin Z, Zhu H L, et al. Practical methods for detection of concealed cracks in highway pavement using ground penetration radar data. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1558-1568. |
| [6] | 刘四新, 曾昭发. 频散介质中地质雷达波传播的数值模拟. 地球物理学报 , 2007, 50(1): 320–326. Liu S X, Zeng Z F. Numerical simulation for Ground Penetrating Radar wave propagation in the dispersive medium. Chinese J. Geophys. (in Chinese) , 2007, 50(1): 320-326. |
| [7] | Millington T M, Cassidy N J. Improving the accuracy of FDTD approximations to tangential components of the coupled electric and magnetic fields at a material interface. IEEE Transactions on Antennas and Propagation , 2011, 59(8): 2924-2932. DOI:10.1109/TAP.2011.2158975 |
| [8] | 冯德山, 陈承申, 戴前伟. 基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟. 地球物理学报 , 2011, 53(10): 2484–2496. Feng D S, Chen C S, Dai Q W. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. Chinese J. Geophys. (in Chinese) , 2011, 53(10): 2484-2496. |
| [9] | 马啸, 杨顶辉, 张锦华. 求解声波方程的辛可分Runge-Kutta方法. 地球物理学报 , 2010, 53(8): 1993–2003. Ma X, Yang D H, Zhang J H. Symplectic partitioned Runge-Kutta method for solving the acoustic wave equation. Chinese J. Geophys. (in Chinese) , 2010, 53(8): 1993-2003. |
| [10] | 罗明秋, 刘洪, 李幼铭. 地震波传播的哈密顿表述及辛几何算法. 地球物理学报 , 2001, 44(1): 120–128. Luo M Q, Liu H, Li Y M. Hamiltonian description and symplectic method of seismic wave propagation. Chinese J. Geophys. (in Chinese) , 2001, 44(1): 120-128. |
| [11] | 孙耿. 波动方程的一类显式辛格式. 计算数学 , 1997(1): 1–10. Sun G. A class of explicitly symplectic schemes for wave equations. Mathematica Numerica Sinica (in Chinese) , 1997(1): 1-10. |
| [12] | Huang Z X, Wu X L. Symplectic partitioned Runge-Kutta scheme for Maxwell's equations. International Journal of Quantum Chemistry , 2006, 106(4): 839-842. DOI:10.1002/(ISSN)1097-461X |
| [13] | Feng K, Qin M Z. Symplectic Geometric Algorithms for Hamiltonian Systems. Hangzhou:Zhejiang Science and Technology Publishing House , 2010: 278-288. |
| [14] | 文舸一. 辛算法及其在电磁场方程中的应用. 微波学报 , 1999, 15(1): 68–79. Wen G Y. Symplectic algorithms and its applications in electromagnetic field equations. Journal of Microwaves (in Chinese) , 1999, 15(1): 68-79. |
| [15] | Liao Z P. Extrapolation non-reflecting boundary conditions. Wave Motion , 1996, 24(2): 117-138. DOI:10.1016/0165-2125(96)00010-8 |
| [16] | 廖振鹏. 工程波动理论导论. 北京: 科学出版社, 2002 . Liao Z P. Introduction to Wave Motion Theories for Engineering (in Chinese). Beijing: Science Press, 2002 . |
| [17] | Hirono T, Lui W W, Yokoyama K, et al. Stability and numerical dispersion of symplectic fourth-order time-domain schemes for optical field simulation. Journal of Lightwave Technology , 1998, 16(10): 1915-1920. DOI:10.1109/50.721080 |
 2013, Vol. 56
2013, Vol. 56

