2. 中国石油勘探开发研究院西北分院, 兰州 730020;
3. 中国科学院地质与地球物理研究所, 北京 100029
2. Research institute of Petroleum Exploration & Development-Northwest, Petrochina, 730020;
3. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing, 100029, China
含盐盆地遍布全球,盐下油气藏主要分布在墨西哥湾、西非海岸盆地、滨里海盆地以及我国塔里木盆地等地区,有巨大的资源潜力,但是勘探难度很大.在盐下地震勘探过程中,地质学家遇到与盐下油气藏勘探有关的理论问题和技术问题.随着对含盐盆地油气勘探的深入,研究目标转向深层盐下构造.由于盐下钻井在费用、技术等方面的原因,盐下构造的精确成像极其重要.在盐丘与沉积围岩速度差较大以及存在多个盐体等情况下,盐下地震速度建模及成像非常困难.
随着盐下勘探开发的需要,成像技术不断地进步.对于盐下复杂构造的成像,常用克希霍夫积分法及单程波波动方程方法.单程波波动方程偏移经波场分解后,波场只能向下或向上传播,波的传播方向受到90°倾角的限制,无法对回转波等特殊波场进行成像,同时单程波方程在描述大角度传播时,相位和振幅都存在误差.为弥补单程波偏移的倾角限制,实际中通常采用克希霍夫积分偏移方法来处理陡倾角地层的成像问题[1].克希霍夫积分偏移虽能适应陡倾角成像,但不能处理单成像点多值走时的问题.另外,克希霍夫积分法只能描述波在光滑介质中的传播.因此,单程波波动方程和克希霍夫积分偏移都无法对复杂构造特别是盐下构造精确成像,地球物理勘探家将目光重新转向逆时偏移.
然而,针对逆时偏移的速度建模又存在难点.通常我们采用克希霍夫积分法建立速度模型,对于复杂的盐丘成像需要对速度建模方法改进,我们提出了多信息约束的速度建模方法.但这并不是最终的目标,严格来讲在角度域开展速度模型更新更加适合逆时偏移成像的需求.
1978年Hemon阐述了有限差分法求解波动方程实现逆时偏移的思想[2],1982年Whitemore[3]真正提出逆时偏移实现方法.此后,Baysal、McMechan等[4-5]将其应用于叠后偏移,因存在艰难的数值计算效率和存储等问题,逆时偏移方法没有进行工业化应用.近年来,GPU/CPU协同高性能计算使3D逆时深度偏移工业化应用成为可能.主要研究工作有两个方面:1)波动方程的逆时外推算法;2)逆时偏移成像条件及计算方法.波动方程逆时延拓算法的研究主要包括波场延拓算子构造、空间和时间差分的频散压制[6](Soubaras,1996)、边界条件构建、成像条件及成像假频噪音压制[7-9]等内容.波动方程逆时外推算法主要是基于有限差分方法求解波动方程的算法.逆时偏移的瓶颈是计算量大,在逆时偏移实现策略方面,国内外学者做了大量研究.2007年,Symes[10]提出在Checking-Points上记录两个时间层的波场.节省存储外推的震源波场的硬盘空间.2009年中科院刘洪、李博及同济大学王华忠基于GPU开展了逆时偏移研究[11-13],应用随机边界思想[14],使炮点波场正向外推过程避免了较大存储和磁盘I/O,在GPU/CPU平台上获得很高加速比.本文在前人研究基础上基于GPU/CPU协同平台,研究并实现了高阶有限差分算法及其稳定性,经数值模型验证其有效性.
2 多信息约束的速度建模方法地震速度建模是一个多信息综合分析的过程[15],国内外对地震速度建模多数采用射线追踪理论及基于角度道集的深度层析速度建模方法[16].速度模型建立方式与地质构造特征有关,由于盐丘形态空间不规则、叠加速度异常等因素导致盐下地震速度建模难度很大.通过研究我们采用多信息约束层控速度建模技术解决了时间域速度异常问题并建立盐下复杂构造速度深度模型.
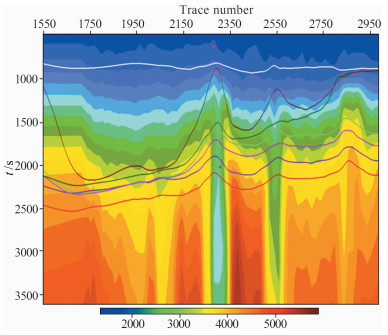
2.1 速度异常分析及校正盐丘是高速地质体,在时间域处理和解释时,会出现盐下构造假象和叠加速度异常等问题.对于海相沉积地层而言,盐下沉积层速度横向变化较稳定.但由于上覆盐丘的影响,使盐下地层的速度场异常,盐丘顶部正下方的位置,速度最低,如图 1.
|
图 1 时间域叠加速度剖面 Fig. 1 Stack velocity profile in time domain |
由图可见,对应于高速异常体下的叠加速度及RMS速度均表现为盐丘两翼速度偏高,中间速度偏低的现象.通过分析,认为产生异常的主要原因是:当上覆盐丘速度与围岩速度差别较大时,远、近炮检距射线穿越地层的速度不同,远、近炮检距时差变化引起叠加速度的变化.由于盐丘速度比围岩的速度高,当炮点移动至盐丘顶部并逐渐移向翼部时,远、近炮检距的时差开始增大,叠加速度开始变小.故在时间域,盐丘高速异常体下伏地层速度异常是正常的地球物理现象[17].但对于深度速度建模而言,若将时间域速度做为初始速度模型时,必须对时间域异常速度进行校正.
在时间域很难估计异常速度的变化趋势和范围,同时速度也存在不确定性.我们采用序贯高斯模拟方法模拟出最大可能的速度结构.序贯高斯模拟的总体思路是沿着随机路径序贯地求取各节点的累计条件分布函数(CCDF),并从CCDF中提取模拟值,获得最大可能的速度.采用趋势约束速度反演方法,解决了时间域速度异常问题并建立了时间域层速度模型,如图 2.

|
图 2 时间域RMS速度剖面(a)和时间域层速度剖面(b) Fig. 2 RMS velocity profile in time domain (a) and interval velocity profile in time domain (b) |
对于盐丘异常区,困扰盐下成像的关键问题仍然是盐丘空间刻画及地震速度建模问题.通过上述方法我们解决了时间域速度异常问题并建立时间域层速度模型.在了解沉积体系及地质信息的基础上,针对陆上盐丘区的地震地质特点,采用层控方法在多井约束下建立深度层速度模型.首先对盐上沉积层建模、盐间碎屑沉积层建模,其次刻画出盐丘的空间分布,最后对盐下沉积层建模.
盐丘复杂构造地震速度建模,主要存在两个难点:1)只利用测井数据(井速度)建模,大范围的盐间速度结构很难得到准确估计;2)若只利用基于模型反演的地震速度建模,则很难反映井附近小尺度结构变化.因此,利用井速度、地震速度变量之间的空间相关性,对其中的几个变量进行空间约束反演估计,如式(1).通过构建克里金方程式(2)求解空间变量最佳约束系数,用井间区域数据(井速度)约束反演地震速度能体现速度纵横向合理的变化.
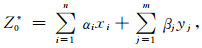
|
(1) |
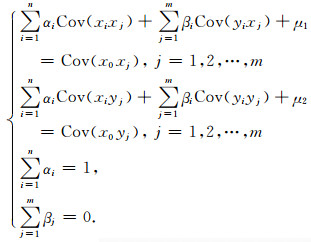
|
(2) |
式中Z0*为空间变量在位置0处的估计值,x1,…,xn为主变量(测井或地质信息)的n个空间样本数据,y1,…,ym为次变量(地震速度)的m个空间样本数据,a1,…,an及β1,…,βm为克里金加权约束系数,Cov(yiyj)为协方差函数.
对于具有明显反射界面及地质构造相对简单的盐上沉积层,模型速度更新采用垂直速度分析和沿层速度分析方法[18].对于盐丘、盐互层及盐间沉积层,速度纵横向变化剧烈,通过3D网格层析成像等多种方法结合优化速度模型,建立精确的速度深度模型,如图 3.

|
图 3 多井约束法建立的速度模型 Fig. 3 Velocity model from multi-well constraint |
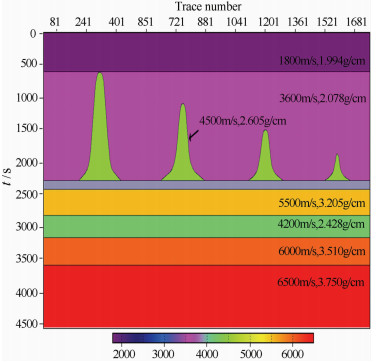
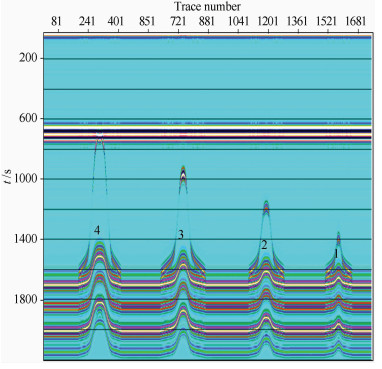
盐丘是高速异常体,由于盐丘速度明显高于围岩速度,盐丘厚度的变化导致盐下构造形态畸变.在地震剖面上表现为:盐丘厚度越大,盐下构造上拉幅度越大,从而导致盐下构造形态与真实地层形态存在较大的差异.通过模型正演技术对构造畸变量进行定量分析,如图 4、图 5.模型参数如下:
|
图 4 复杂盐丘理论模型 Fig. 4 Theoretical model of complex salt dome |
|
图 5 模型正演的零偏移距剖面 Fig. 5 Zero offset profile after forward modeling |
第一层:V1=1800 m/s,p=1.994 g/cm3,H=0~600 m;
第二层:V2=3 600 m/s,p=2.078 g/cm3,H=600~2200 m,其中盐丘Vsalt=4500 km/s,p=2.605 g/cm3;
第三层:V3=3 900 m/s,p=2.552 g/cm3,H=2200~2300 m;
第四层:V4=5500 m/s,p=3.205 g/cm3,H=2300~2700 m;
第五层:V5=4200 m/s,p=2.428 g/cm3,H=2700~3100 m.
如图 5正演结果与实际地震剖面特征一致,在盐下各反射层上拉形成较大幅度的背斜构造,且构造幅度与盐丘厚度有关.为了定量描述盐下构造及圈闭幅度,分别对盐丘厚度及速度对上拉幅度的影响进行了理论分析.
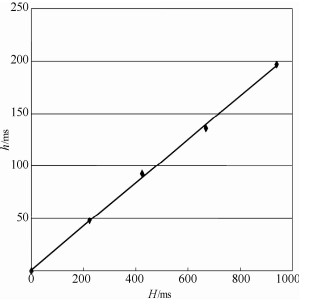
1) 假定盐岩速度为4 500 m/s、围岩速度3 600 m/s均不变的情况下,改变盐岩厚度.分别取盐丘厚度为500m、1000m、1500m、2000m四个盐丘,正演计算盐下构造幅度及反射时间,如图 6.由统计结果可看出,盐下地层上拉幅度与盐丘厚度具有一定线性关系,即厚度每增加100m,盐下构造上拉幅度增大约12ms.
|
图 6 盐丘厚度与构造幅度理论分析 Fig. 6 Theoretical analysis of salt thickness and structure extent |
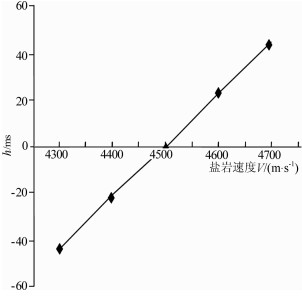
2) 假定盐丘和围岩厚度不变(盐丘高度2000m,围岩速度3 600 m/s),改变盐岩速度.盐岩速度分别取4 300 m/s、4 400 m/s、4 500 m/s、4 600 m/s、4 700 m/s.由统计结果可看出,盐下地层上拉幅度同样与盐岩速度具有一定线性关系,盐岩速度每增加或减小100 m/s,盐下构造上拉幅度增大或减小约19ms,如图 7.
|
图 7 盐岩速度与构造幅度理论分析 Fig. 7 Theoretical analysis of salt velocity and structure extent |
通过上面的理论分析,结合多口井的VSP数据,认为盐岩的层速度应介于4 400~4 600 m/s之间,纯盐岩层速度为4 500 m/s.从定量分析结果来看,无论盐层充填速度为4 400 m/s还是4 700 m/s,对盐下构造影响较小,只有20m s,但盐丘的厚度变化很大,有的甚至超过2000m.综合分析认为,影响盐下地层构造形态变化的主要因素是盐岩的厚度.因此,要落实盐下真实构造形态,必须准确刻画盐丘空间分布,建立精确速度-深度模型.
3 盐下构造逆时偏移成像研究克希霍夫积分偏移能适应陡倾角成像.采用程函方程算法时,方程只计算最快的波至时间.当对盐下成像时,会有许多不同的到达路径.若采用射线追踪算法,计算能量最强的波至时,在盐下阴影区域,能量最强的波至可能在穿越盐体时发生延迟,盐下成像效果不好.单程波方程在描述大角度传播时,成像误差较大,不能对陡倾角反射精确成像.通过研究,我们采用双程波波动方程深度域成像技术解决了盐下成像问题,实现了对盐丘边界及盐丘侧翼的准确归位,使盐下地层在深度域能够准确成像.
逆时偏移方法是通过双程波波动方程在时间域对人工给予的震源子波正向传播和接收到的地震资料进行反向传播,结合相关成像条件实现偏移(Claerbout,1971)[19].相对于单程波场延拓而言,逆时偏移运用的是双程波进行波场延拓,避免了上下行波的分离处理,因而成为最准确的成像算法,且不受倾角的限制,并能实现回转波和多次波成像.
3.1 波场外推方法三维介质双程声波方程为
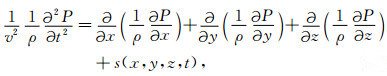
|
(3) |
式中,P=P(x,y,z,t)为介质中的压力场,ρ=ρ(x,y,z)为介质密度,v=v(x,y,z)为速度场,s(x,y,z,t)为震源项.
Dablain(1986)详细地讨论了三维双程波动方程的高阶有限差分解法[20].本文在此基础上研究了正向和逆时外推的计算公式.利用时间二阶中心有限差分近似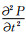
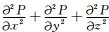
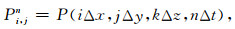
|
i,j,k,n分别代表x,y,z,t对应的离散点序号,Δx,Δy,Δz分别为沿x,y,z轴的空间采样间隔,Δt为时间步长.P(x,y,z,t)对x的二阶偏导数
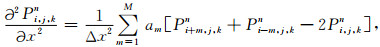
|
(4) |
式中am为差分系数,不同阶数其值见表 1.
|
|
表 1 部分阶数有限差分算子的差分系数 Table 1 Differential coefficients of operatars |
当M>2时,am表示为
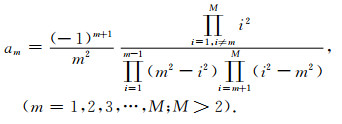
|
(5) |
同理可推导出P(x,y,z,t)对y,z及时间t的2M阶精度中心差分格式:
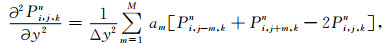
|
(6) |
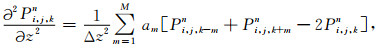
|
(7) |
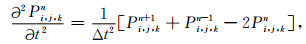
|
(8) |
将(6)~(8)式带入(3)得到M阶空间差分正演方程
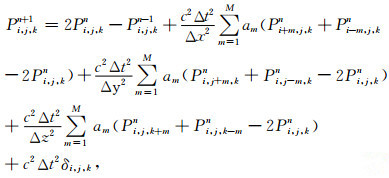
|
(9) |
δi,j={f(n),i=is,j=js,k=ks0,i≠is,或j≠js,或k≠ks式中δi,j为震源项,f(n)为离散的震源函数,is,js,ks分别为震源点对应的x,y,z方向的网格点序号.
波场的反向延拓过程是已知后两个时刻波场推前一个时间的波场,其计算过程可表示为
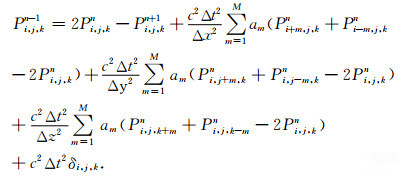
|
(10) |
式(9)与式(10)分别为截断误差为O(Δx2M,Δy2M,Δz2M,Δt2)的三维正反演高阶差分方程.通过上述方程及系数,可得出某一种截断误差的高阶差分方程.若分别用Δx,Δy,Δz表示空间差分网格的间距、Fmax表示震源子波最大频率、Vmin表示最小速度,则差分格式的频散条件可表示为
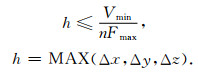
|
(11) |
逆时偏移成像条件方面,Claerbout(1971)提出上、下行波相关成像条件.但逆时偏移成像是用双程波方程逆时外推波场与沿正时间方向外推的震源波场在空间任何一点进行零延迟的互相关.从传播路径看,这两个波场从炮点到反射点,再到检波点的整个路径上都是相关的.因此,逆时偏移产生很强的低频噪音. Mulder[21](2003)提出对成像结果高通滤波可以消除假象;Yoon,et al.(2004)提出通过对成像条件引入与角度有关的震源与检波点波场的信息来挑出合适成像结果,进而去除假象[22];Fletcher,et al.(2005)把特定区域引入方向阻尼,来压制假象[23];Liu,et al(2007a)提出波场分解的成像条件[24-26].本文应用Claerbout的互相关成像原理,然后用Laplace滤波消除低频假象[27].互相关成像条件的成像公式表示为
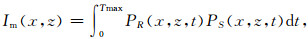
|
(12) |
式中的被积函数PR(x,z,t)PS(x,z,t)表示t时刻对整个波场做一次成像运算,积分说明像空间Im(x,z)中的像是时间步所成的像的叠加.为了实现相关成像,需要先算出最后时刻的炮点波场,在此我们利用随机边界条件方法(Clapp,2009),从零时刻算到最后时刻,从最后时刻波场反推波场,虽然计算量加大了,但由于减少了GPU与内存的数据通讯量和磁盘存储量,用GPU实现,整体的计算速度明显提高.
3.3 理论模型试算本文设计了盐丘模型来测试叠前逆时偏移成像方法的精度及适用性.该模型数据观测参数为:439炮,每炮160道,炮间距100m,道间距10m,偏移距-8000~8000m,记录长度6.0s,采样点数3001,时间采样率2ms,如图 8.
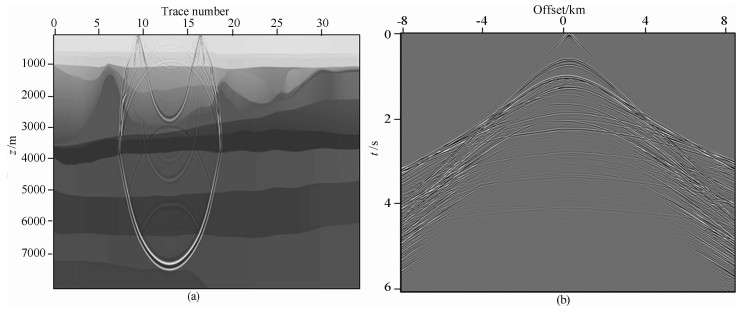
|
图 8 盐丘模型正演波场(a)及正演单炮(b) Fig. 8 Wave field of salt dome model of forward modeling (a) and single shot (b) |
数值试验偏移参数为:主频:20 Hz;偏移孔径:Aperture_x=10000m:成像输出间隔:Dx=Dy=10m,Dz=10m,Nz=801.偏移时效对比:采用60节点CPU系统总耗时520 min;采用12节点GPU/CPU协同系统(S2090),总耗时28 min.因此,单节点加速比:GPU:CPU=92.86:1.通过试算该算法不仅具有高效的加速比,而且成像精度最高,如图 9.
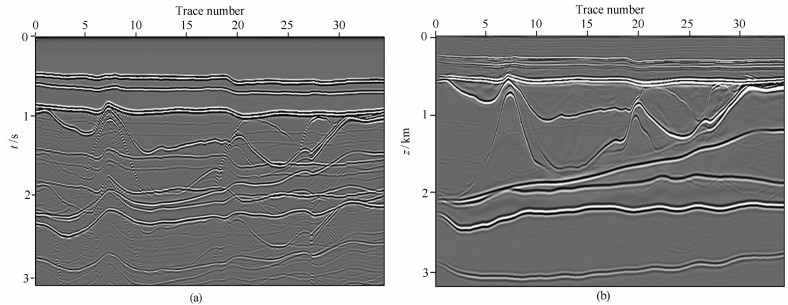
|
图 9 盐丘模型零偏移距剖面(a)及逆时偏移成像结果(b) Fig. 9 Zero-offset profile of salt dome model (a) and reverse time migration result (b) |
从9图可看出,在速度模型准确时,深度域成像都能恢复盐下地层真实构造形态,但对于盐丘等特殊构造,逆时偏移通过对复杂速度结构的波场精确传播,能使盐丘的顶界、底界及陡倾角侧翼地层精确成像.
3.4 实际资料试验由于盐丘速度与围岩地层速度差异大,且盐丘厚度横向变化大,造成地震波场复杂及时间域构造假象等问题.针对陆地H区复杂盐丘的地质特征,采用层控多信息约束地震速度建模方法,建立盐丘速度-深度模型,如图 4.采用双程波波动方程深度域成像技术解决盐下、盐丘侧翼的成像问题.
从逆时偏移成像结果中可看出,双程波波动方程深度域成像技术解决了盐下、盐丘侧翼的成像问题,实现了对盐丘边界及盐丘侧翼的准确归位,消除了盐丘速度异常对下伏地层造成的时间域构造畸变,使盐下地层在深度域能够准确成像.盐丘顶界面、盐侧翼边界、大于90°盐侧翼特殊盐下构造能精确成像,如图 10.陡峭的盐岩侧翼波至(也许来自向上转折的界面),这些同相轴可能来自棱镜波照明[28].像盐丘这样的复杂地质体是用多种波道来照明的,这些盐体不能用常规单程传播算子来成像.通过采用双程波动方程偏移方法,处理陡倾角和回折波能量及来自其他双程射线路径的能量,能使回转构造成像,明显改善盐丘侧翼及盐下的成像.
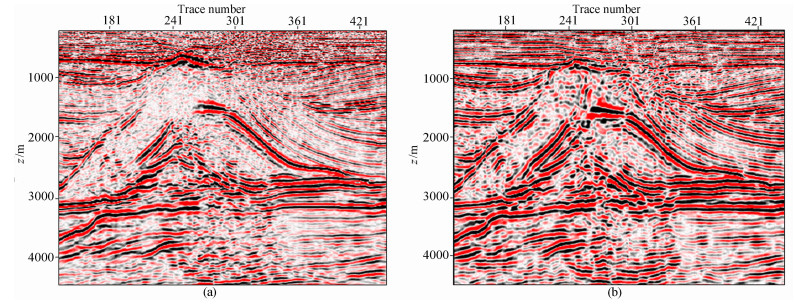
|
图 10 盐下构造单程波偏移(a)与逆时偏移成像结果对比(b) Fig. 10 One-way migration (a) and reverse time migration of sub-salt structure (b) |
速度建模与偏移算法的结合是复杂构造精确成像的关键.逆时偏移是当前精度最高的深度域成像方法,能使高角度反射界面的反射波,甚至超过90°反射界面精确成像.
4.2本文采用层控建模技术进行实体建模;采用序贯高斯模拟及克里金约束速度反演方法,解决了时间域速度异常问题;结合地质、测井信息采用层控多信息约束地震速度建模技术,建立盐丘速度深度模型.同时基于GPU/CPU协作平台,将波场延拓通过GPU实现,采用双程波波动方程深度域成像技术解决了盐下、盐丘侧翼的成像问题,实现了对盐丘边界及盐丘侧翼的准确归位,消除了盐丘速度异常对下伏地层造成的时间域构造畸变,使得盐下地层在深度域能够准确成像.
4.3在实际资料处理中,我们首次实现大面积逆时偏移工业化生产,取得良好的成像效果.因此,GPU/CPU协同并行计算及逆时偏移将成为未来高性能计算及成像的主流,将在地震叠前成像领域发挥重要作用.
致谢感谢中国科学院地质与地球物理研究所李博、刘红伟博士在科研中给予的指导和帮助!感谢同济大学王华忠老师、赵磊博士在科研中给予的指导与帮助.
| [1] | 丁亮, 刘洋. 逆时偏移成像技术研究进展. 地球物理学进展 , 2011, 26(3): 1085–1100. Ding L, Liu Y. Progress in reverse time migration imaging, Progress in Geophys. (in Chinese) (in Chinese) , 2011, 26(3): 1085-1100. |
| [2] | Hemon CH. Equations d'onde et modeles. Geophysical Prospecting , 1978, 26(4): 790-821. DOI:10.1111/gpr.1978.26.issue-4 |
| [3] | Whitmore D W. Iterative depth migration by backward time propagation.//53rd Annual International Meeting, SEG, Expanded Abstracts, 1983, 382-385. |
| [4] | Baysal E, Kosloff D D, Sherwood J W C. Reverse time migration. Geophysics , 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [5] | McMechan G A. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting , 1983, 31(3): 413-420. DOI:10.1111/gpr.1983.31.issue-3 |
| [6] | Soubaras R. Explicit 3-D migration using equiripple polynomial expansion and Laplacian synthesis. Geophysics , 1996, 61(5): 1386-1393. DOI:10.1190/1.1444062 |
| [7] | Zhang Y, Sun J C, Gray S H. Aliasing in wavefield extrapolation prestack migration. Geophysics , 2003, 68(2): 629-633. DOI:10.1190/1.1567232 |
| [8] | 徐琴, 李振春, 鲍伟. 波动方程偏移中的成像条件研究进展. 勘探地球物理进展 , 2008, 31(4): 247–252. Xu Q, Li Z C, Bao W. Progress in rearch of imaging condition for wave equation migration. Progress in Exploration Geophys. (in Chinese) , 2008, 31(4): 247-252. |
| [9] | 许璐, 孟小红, 刘国峰. 逆时偏移去噪方法研究进展. 地球物理学进展 , 2012, 27(4): 1548–1556. Xu L, Meng X H, Liu G F. Reverse time migration and removing artifacts. Progress in Geophys. (in Chinese) , 2012, 27(4): 1548-1556. |
| [10] | Symes W W. Reverse time migration with optimal checkpointing. Geophysics , 2007, 72(5): SM213-SM221. DOI:10.1190/1.2742686 |
| [11] | 李博, 刘国峰, 刘洪. 地震叠前时间偏移的一种图形处理器提速实现方法. 地球物理学报 , 2009, 52(1): 245–252. Li B, Liu G F, Liu H. A method of using GPU to accelerate seismic pre-stack time Migration. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 245-252. |
| [12] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [13] | 李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报 , 2010, 53(12): 2938–2943. Li B, Liu H W, Liu G F, et al. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 2938-2943. |
| [14] | Clapp R G. Reverse time migration with random boundaries.//79th Annual International Meeting, SEG Expanded Abstracts, 2009, 28, 2809-2813. http://www.oalib.com/references/18983603 |
| [15] | 王西文, 刘全新, 苏明军, 等. 多井约束下的速度建模方法和应用. 石油地球物理勘探 , 2003, 38(3): 263–267. Wang X W, Liu Q X, Su M J, et al. Multi-well constrained velocity model-building method and its application. Oil Geophysical Prospecting (in Chinese) , 2003, 38(3): 263-267. |
| [16] | 秦宁, 李振春, 杨晓东, 等. 叠前多级优化联合偏移速度建模. 地球物理学进展 , 2013, 28(1): 0320–0328. Qin N, Li Z C, Yang X D, et al. Pre stack joint migration velocity modeling with multi stage optimization. Progress in Geophys. (in Chinese) , 2013, 28(1): 0320-0328. |
| [17] | 温铁民, 苏世龙, 钱豫. 盐下速度场异常问题分析. 石油地球物理勘探 , 2007, 42(S1): 5–7. Wen T M, Su S L, Qian Y. Analysis of abnormal issue in subsalt velocity field. Oil Geophysical Prospecting (in Chinese) , 2007, 42(S1): 5-7. |
| [18] | 王西文, 刘文卿, 王宇超, 等. 共反射角叠前偏移成像研究及应用. 地球物理学报 , 2010, 53(11): 2732–2738. Wang X W, Liu W Q, Wang Y C, et al. Research and application of common reflection angle domain pre-stack migration. Chinese J. Geophys. (in Chinese) , 2010, 53(11): 2732-2738. |
| [19] | Claerbout J. Toward a unified theory of reflector mapping. Geophysics , 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [20] | Dablain M A. The application of high-order differencing to the scalar wave equation. Geophysics , 1986, 51(1): 54-66. DOI:10.1190/1.1442040 |
| [21] | Mulder W, Plessix R. One-way and two-way wave-equation migration.//Expanded Abstracts of 73rdAnnual International Meeting, SEG, 2003, 881-884. http://www.oalib.com/references/19002037 |
| [22] | Yoon K, Marfurt K J, Starr W. Challenges in reverse-time migration.//74th Annual International Meeting, SEG, Expanded Abstracts, 2004, 1057-1060. http://www.oalib.com/references/19002038 |
| [23] | Fletcher R, Fowler P, Kitchenside P, et al. Suppressing unwanted internal reflections in prestack reverse-time migration. Geophysics , 2006, 71(6): E79-E82. DOI:10.1190/1.2356319 |
| [24] | Liu F Q, Morton S A, Leveille J P, et al. Reverse-time migration using one-way wavefield imaging condition.//Expanded Abstracts of 77th Annual International Meeting, SEG, 2007, 2170-2174. http://www.oalib.com/references/19002040 |
| [25] | 徐兴荣, 王西文, 王宇超, 等. 基于波场分离理论的逆时偏移成像条件研究及应用. 地球物理学进展 , 2012, 27(5): 2084–2090. Xu X R, Wang X W, Wang Y C, et al. Study and application of imaging condiation for reverse time migration base on wave fields separation. Progress in Geophys. (in Chinese) , 2012, 27(5): 2084-2090. |
| [26] | Symes W W. Mathematical foundations of reflection seismology. Technical Report, Rice University, 1995. |
| [27] | Zhang Y, Sun J. Practical issues of reverse time migration:true amplitude gathers, noise removal and harmonic-source encoding. CPS/SEG Beijing2009 International Geophysical Conference & Exposition, 2009, ID:5. http://www.oalib.com/references/18991955 |
| [28] | 陈波, 何文华, 吴林钢, 等. 盐下地震勘探实践和认识. 石油地球物理勘探 , 2007, 42(S1): 90–92. Chen B, He W H, Wu L G, et al. Practice and knowledge of subsalt seismic exploration. Oil Geophysical Prospecting (in Chinese) , 2007, 42(S1): 90-92. |
 2013, Vol. 56
2013, Vol. 56

