传统地震仪可以监视地震发生、记录地震波信号等相关信息, 为快速确定地震震中、震级以及地震预警提供宝贵的观测资料.地震仪主要有宽频带地震仪(速度型地震仪)和强震仪(加速度型地震仪)两种, 在应用中主要存在两个问题:一是宽频带地震仪遇到强震时经常会超出记录量程, 无法完整的记录地震波波形; 二是在地震和海啸预警研究中, 地震仪数据通常需要积分为位移量计算震级和海啸高度[1-2], 但受仪器倾斜、旋转等因素影响, 积分结果会引入许多误差, 难以获得准确的地壳形变信息.以上两个问题是造成地震震级确定误差的主要原因之一.例如, 2011年3月11日, 日本发生Mw9.0级大地震(东日本大地震), 但是日本气象厅(JMA)1 h后速报的震级仅为Mw8.4, 3天后才修订为Mw9.0.速报震级偏小, 导致日本相关部门对地震引起的海啸高度预报偏低, 最终造成日本东北部沿海地区应对海啸准备不足, 增加了大量的人员伤亡和财产损失.
近年来, 随着高频GNSS接收机(1~50 Hz)的出现和精密定位技术的发展, 利用高频GNSS数据恢复地震时期地表瞬时动态形变信息和地震波信号的研究已较为成熟.2003年, Larson等成功利用实测的高频GPS数据采用JPL研发的GIPSY软件恢复了2002年Delali地震的远场地震波[3]. Kouba采用PPP方法处理了此次地震期间的IGS跟踪站网1HzGPS数据, 表明PPP方法同样可以获得地震波信号[4].随后, 高频GNSS数据恢复地震波信号的研究得到了迅速发展[5-6], 其结果也被用于震源破裂过程、震源参数反演、断层滑动分布等研究中[7-9], 并发展为一门新的学科——“GNSS地震学”[10]. GNSS作为记录地震波信号的一种新型仪器, 也被称为“GNSS地震仪”.
然而, 上述研究主要基于事后处理模式, 若要利用GNSS观测结果实现地震参数实时确定及地震预警, 需要提供实时的GNSS数据处理结果.一种能够实现GNSS数据实时解算及地震波信号实时探测的系统, 本文称之为“实时GNSS地震仪系统”. GNSS实时精密定位是实现该系统的关键技术. GNSS实时精密定位主要有两种模式, 即实时相对定位和实时精密单点定位(Real-time Precise point positioning-RTPPP)模式.实时相对定位需要至少一个测站作为参考站, 当大地震发生时, 地震波的波及范围可达到几百甚至上千公里, 很难快速实时地选择完全静止的参考站. RTPPP模式采用单台接收机实现精密定位, 定位方式灵活, 适合实时定位处理[11]. JPL实施的实时地震和海啸预警工程(GREAT)旨在采用RTPPP方法实现全球范围cm级精度定位服务, 用于自然灾害监测和预警(http:∥www.gdgps.net/products/greatalert.html. Allen等将实时GPS数据获得的地震波结果与利用加速度和速度计获得的结果进行对比, 表明实时高频GPS数据能够用于地震震级确定和地震预警[12].张小红等利用精密单点定位采用仿实时模拟的方式, 获得了汶川地震GPS测站的定位结果[13].但是, 这些研究未对GPS获得的地震波信号进行定量的精度评定.本文将基于RTPPP方法, 构建实时GNSS地震仪系统, 并通过模拟震动平台和实测地震数据, 定量分析GNSS地震仪系统的精度.
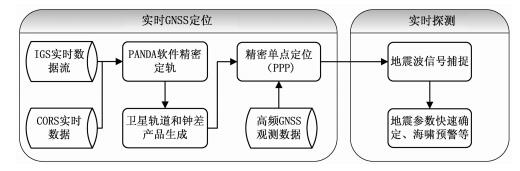
2 实时GNSS地震仪系统构成本文构建的实时GNSS地震仪系统主要包括实时GNSS定位和实时地震信号探测两个部分.其中实时GNSS定位部分包括实时数据流的接收、轨道和钟差产品生成、产品播发和用户端实时定位.实时地震信号探测部分主要是利用GNSS实时定位结果探测并捕捉地震波信号.系统原型如图 1所示.
|
图 1 实时GNSS地震仪系统原型 Fig. 1 A prototype of real-time GNSS seismometer system |
本文构建的实时GNSS地震仪系统采用RTPPP方法进行精密定位. RTPPP方法需要实时获得高精度的卫星轨道和钟差产品, 目前国际GNSS服务组织(IGS)提供预报的卫星轨道和钟差产品(IGU产品)其预报部分的轨道精度为5cm, 钟差精度仅为3 ns, 无法满足高精度mm-cm级实时定位的需求.因此, 需要通过精密定轨获得高精度实时卫星轨道和钟差产品, 然后通过数据播发模块发送给用户用于实时精密定位.
2.1.1 实时数据流接收2007年6月, IGS开展了IGS实时实验计划(Real Time Pilot Project, RTPP), 主要目标包括:管理和维护IGS的实时跟踪站网络; 生成组合的IGS实时分析产品; 研究出一套标准的实时数据接收和发布格式; 制定实时分析产品的标准格式.该计划旨在形成一套完整的IGS实时产品服务系统(http:∥igscb.jpl.nasa.gov/).
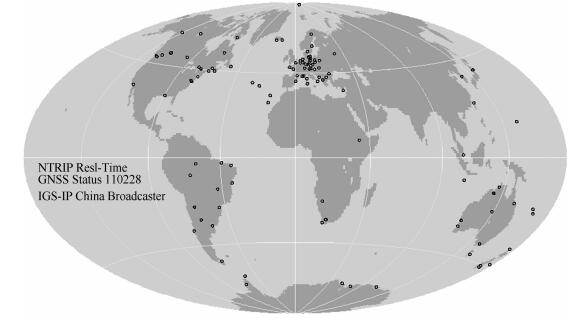
武汉大学卫星导航定位技术研究中心自2009年开始参与RTPP计划, 并于2009年6月, 由IGS实时数据流工作组BKG的GNSSd at acenter授权在武汉大学卫星导航定位技术研究中心成立了亚太地区最早的数据转发中心(http:∥ntrip.gnsslab.cn). 图 2为武汉大学实时数据中心转发的GNSS实时基准站分布图, 这些基准站实时数据流是实现实时精密定轨获得实时精密轨道和卫星钟差的数据基础.
|
图 2 武汉大学实时数据中心转发的GNSS基准站分布图 Fig. 2 Distribution of real-time reference stations distributed from Wuhan University |
目前一些数据处理中心已可以提供实时的钟差产品:BKG分析中心实时获取跟踪站网络的高采样率实时数据流, 采用RTNet软件开展了秒级更新的实时钟差估计工作, 钟差精度优于0.5 ns [14]; ESA采用基于扩展卡尔曼滤波开发的Auto-BAHN软件可以提供精度为0.3 ns的5s更新的钟差产品[15].
武汉大学自主研发的PANDA(Positioning And Navigation Data Analyst)软件具有实时定轨功能, 能为用户提供实时轨道精度3~5mm和钟差精度0.1~0.3 ns的产品[16-17].具体过程是:(1)接收图 2中显示的GNSS基准站的实时数据流, 利用基准站实时数据流管理软件实现对实时观测数据流的接收、时间同步处理, 并将实时数据流发送至轨道和钟差处理端; (2)利用获取的基准站实时数据精密定轨, 获得卫星精密轨道; (3)固定利用PANDA软件定轨获得的精密轨道, 同时强约束测站坐标, 模糊度参数通过历元间差分方法进行消除, 参数估计采用平方根信息滤波, 估计参数包括卫星钟差历元间的变化、接收机钟差历元间的变化以及对流层参数.由于通过历元间差分方法估计的是卫星钟差历元间的变化, 因此需引入一参考历元的卫星钟差初值, 该初值可采用广播星历计算得到.
2.1.3 数据通信和产品播发数据通信协议采用通用的Ntrip协议与TCP/IP协议两种方式连接.这两种方式应用于不同的情况:一, 对具有管理控制功能的实时跟踪站接收机, 直接采用TCP/IP协议与数据处理中心进行连接; 二, 实时跟踪站接收机通过服务器转发与客户端数据连接软件连接, 采用Ntrip协议.数据格式主要包括RTCM2.0、RTCM3.0以及接收机原始二进制格式.
卫星轨道与钟差产品可采用多种播发方式, 主要包括GPRS、3G等Internet传输和同步通信卫星播发, 本系统采用3G传输播发方法.
2.1.4 实时精密单点定位利用PANDA计算的实时精密卫星轨道和钟差产品, 在用户端实时接收并对观测站高频GNSS数据进行实时精密单点定位, 可获得观测站逐历元定位结果.具体过程为:自接收机获得实时观测数据后, 利用服务端发送的轨道和钟差信息改正广播星历的卫星轨道误差以及卫星钟误差, 观测值采用双频无电离层组合观测值(LC), 利用模型改正潮汐误差, 相位偏差、对流层延迟等, 其中对流层延迟改正采用Saastamoinen模型加GMF投影函数[18], 残余的天顶对流层延迟误差采用随机游走方法进行实时估计.最后采用卡尔曼滤波实时估计测站坐标和模糊度等参数.
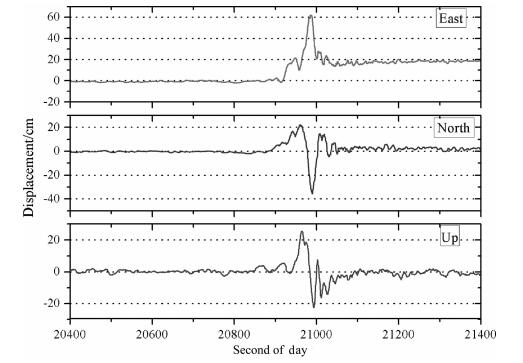
2.2 实时探测高频GNSS数据通过RTPPP方法解算可以实时获得观测站逐历元动态定位结果.当定位结果收敛以后, 测站坐标时间序列将处于平稳状态.一旦测站位置发生变化, RTPPP定位结果将实时反映测站运动轨迹. 图 3为2011年东日本大地震USUD站的RTPPP处理结果, 当地震波到达前, RTPPP结果处于平稳状态, 一旦地震波到达测站, RTPPP结果将实时反应测站瞬时运动情况.从图中我们发现, E方向不仅包含动态的地震波形, 还存在20cm的永久性偏移, 说明高频GNSS数据不仅可以捕获地震波信号, 还可以测定测站永久性偏移量.这些信息可以为地震参数快速确定和地震预警提供更加可靠的观测资料和判断依据.
|
图 3 2011年东日本大地震USUD站获得的地震波信号 Fig. 3 Displacement waveforms derived from USUD station in 2011 Tohoku-Oki earthquake |
为了定量评估实时GNSS地震仪系统的精度, 本文分别利用模拟震动实验平台试验数据和Baja California地震数据进行分析.
3.1 震动实验平台为研究GNSS动态定位精度, 我们构建了震动实验平台[19], 如图 4所示.该实验平台由8根弹簧将一块铝板固定在金属框架上, 铝板上可同时承载GNSS接收机天线、加速度计和惯导设备(IMU)等多种仪器设备.通过外力作用于铝板, 平台可在三维空间6个自由度方向运动.

|
图 4 模拟震动试验平台 Fig. 4 A shaking table platform with GNSS and IMU |
本次实验采用的仪器包括一台Trimble NetR8 GNSS接收机, 接收的数据设置为该仪器的最高采样率50 Hz, 一台惯导设备(IMU), 设置的数据采样率为250 Hz.如图 4所示, GNSS1为Trimble NetR8 GNSS接收机的天线, 而另一个接收机天线(GNSS2)为IMU提供时间脉冲和加速度漂移校正, 该GNSS接收机的采样率为1 Hz.
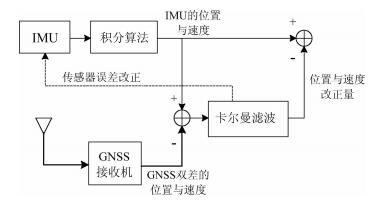
IMU设备本身即可提供平台的瞬时运动位置信息.IMU包括加速度计和陀螺仪, 前者测量加速度(以及重力, 合称比力), 后者测量角速度(或角度变化).IMU的测量信息可以通过积分运算得到运载体位置、速度和姿态信息, 但是IMU传感器存在误差且其积分误差随时间无限发散, 因此需要额外的辅助信息来抑制发散现象, 本实验采用GNSS/IMU组合方式获得载体运动位置信息, 其处理流程如图 5所示.其中GNSS辅助信息采用双差相对定位获得天线GNSS2的位置与速度.相对定位采用的GNSS基准站距离震动实验平台约400m, 采样率为1Hz.而IMU测量获得震动平台的加速度和姿态信息, 通过积分算法获得IMU的位置与速度, 结合GNSS相对定位结果, 采用卡尔曼滤波估计方法, 最终获得震动平台的瞬时运动位置信息.
|
图 5 GNSS/IMU组合定位流程图 Fig. 5 GNSS/IMU positioning processing flow char |
本文将IMU获得的平台运动位置信息作为参考, 验证RTPPP方法的定位精度.由于IMU与GNSS1在震动平台上的摆放位置不相同, 两者之间存在一个杆臂向量, 因此要通过杆臂改正将IMU得到的定位信息转换到GPS所处的位置, 并将坐标结果由地固系(X/Y/Z)转换至站心坐标系(E/N/U).
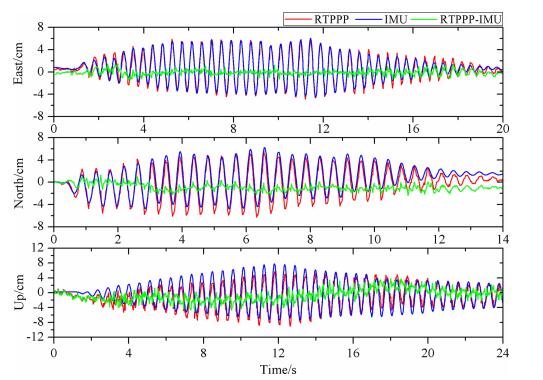
RTPPP计算流程如2.1节所述, 实时精密轨道和钟差产品由PANDA软件提供, 轨道和钟差差分数每秒播发一次.用户端实时接收播发的产品采用PPP方法可实时获得震动平台实时运动结果.为了比较RTPPP和IMU结果, 坐标结果均由地固系(X/Y/Z)转换至站心坐标系(E/N/U). 图 6为其中一组震动实验的RTPPP(红线)与IMU(蓝线)结果, 为定量分析RTPPP精度, 计算了RTPPP与IMU结果的互差(绿线所示).通过统计, E、N、U方向互差RMS值分别为7.4mm、6.2mm和16.9mm.从图中U方向的结果可以看出, 尽管RTPPP结果表现出一定的长周期趋势项, 但短时间内(数分钟)精度较高, 同样完整地恢复了震动平台的震动波形.而在实时地震监测和地震波信号提取研究中, 主要关注的是短时间内相对变化量和振动波形, 因此, RTPPP在短时间内的高精度正好可以满足地震实时监测和地震波获取的需求.
|
图 6 平台震动RTPPP与IMU结果及互差 Fig. 6 Displacements of platform movements derived from RTPPP and IMU and their difference |
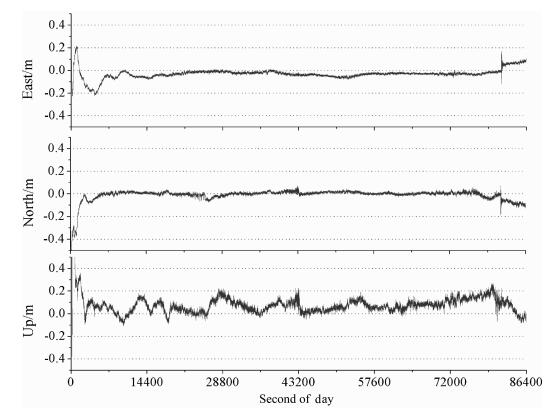
为了实现实时GNSS地震仪系统在实际地震中的运用, 本文对2010年4月4日(UTC时间22:40:42)墨西哥北部发生的Ms7.2级Baja California地震进行研究.美国南加州区域布设的GPS测站记录了本次地震的发生过程, 为此次地震研究提供了宝贵的观测资料.利用本文介绍的RTPPP方法, 以模拟实时的方式重新处理了Baja California地震期间共4个测站的1 Hz高频GPS数据, 为便于分析, 均转换为站心坐标系(E/N/U). 图 7为P500站RTPPP计算的E、N、U方向结果.
|
图 7 测站P500单天RTPPP结果 Fig. 7 RTPPP results for one day on station P500 |
为了定量分析RTPPP结果的精度, 分别与事后PPP结果以及相对定位(DD)结果进行对比.事后PPP结果利用PANDA软件计算得到, 精密星历采用CODE分析中心提供的事后精密轨道和钟差产品, 利用模型改正潮汐误差, 相位偏差、对流层延迟等, 其中对流层延迟改正采用Saastamoinen模型加GMF投影函数, 残余的天顶对流层延迟误差采用随机游走方法进行估计, 电离层延迟采用双频无电离层组合消除, 最后通过最小二乘方法估计测站坐标、接收机钟差和模糊度等参数.具体计算策略详见参考文献[6].
相对定位(DD)结果采用南加州地震数据中心(SCEDC)公布的结果.美国地质调查局(USGS)和南加州地震研究中心(SCEC)等机构共同建立的南加州地震数据中心提供了此次地震期间GPS数据解算的测站坐标时间序列, 其数据处理方式为相对定位模式[20], (http:∥www.data.scec.org/research/MayorCucapah20100404/Mexicali_GPSsac.tar.gz).
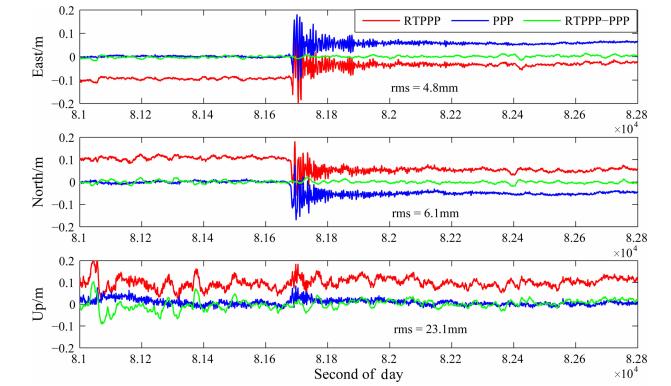
图 8给出了P500站地震前后共半小时(22:30-23:00)的RTPPP与事后PPP结果以及两者的差值, 图 9为RTPPP与DD结果比较结果.
|
图 8 P500测站RTPPP与事后PPP结果比较 Fig. 8 Displacement on station P500 derived from RTPPP and PPP and their differences |
|
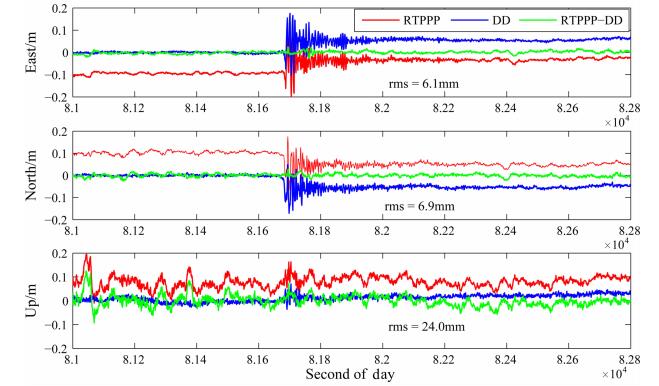
图 9 P500测站RTPPP与双差(DD)结果比较 Fig. 9 Displacements on station P500 derived from RTPPP and relative positioning and their differences |
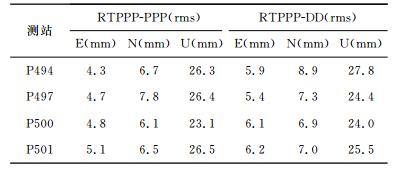
4个测站地震前后共半小时(22:30-23:00)的RTPPP与事后PPP、RTPPR与DD结果比较见表 1.经统计, RTPPP与事后PPP互差RMS水平方向为4~8 mm, 优于1cm, 高程方向为23~27mm, 优于3cm; RTPPP与相对定位(DD)结果互差rms水平方向为5~9mm, 优于1cm, 高程方向为24~28mm, 优于3cm.
|
|
表 1 RTPPP与PPP和DD结果的互差rms Table 1 Difference (rms) between RTPPP and PPP and Difference (rms) between RTPPP and DD |
详细分析图 9中可以发现, RTPPP结果在水平方向的精度与事后PPP和DD结果相差较小(优于1cm), 而高程方向与事后PPP和DD结果有较大差别, 且主要呈现长周期特性, 主要是受预报的轨道和钟差精度、以及对流层延迟的影响.而DD结果通过差分方法有效消除了轨道、卫星钟差及对流层延迟等误差影响.
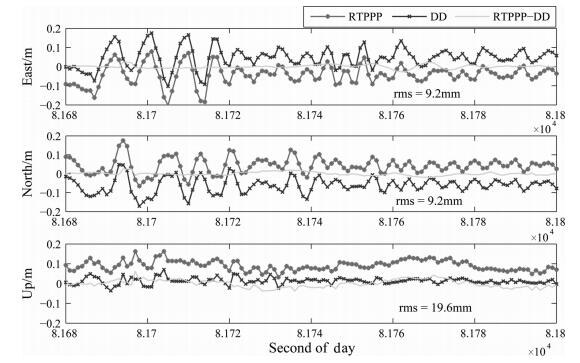
图 10为P500测站地震前后2min的RTPPP与DD的结果, 此次地震造成的P500测站水平方向振幅约20cm, RTPPP获得的水平方向地震波形与DD结果非常一致.而高程方向振幅约为5cm, 且RTPPP结果在U方向表现的震动波形与DD结果基本一致, 说明RTPPP对于振幅为5cm的高程方向运动也具有监测能力.
|
图 10 P500测站RTPPP与双差(DD)地震前后2min结果比较 Fig. 10 Displacements on station P500 derived from RTPPP and relative positioning and their differences (2 minutes) |
本文构建的实时GNSS地震仪系统采用RTPPP方法能获取高精度的测站瞬时地表形变和地震波, 该方法采用单站独立测量模式, 具有很好的定位灵活性.当RTPPP收敛后, 统计半小时观测时段, 其定位精度水平方向优于1cm, 高程优于3cm. RTPPP结果在水平方向的精度与事后PPP和DD结果相当, 而高程方向与事后PPP和DD结果相比, 主要存在长周期特性误差的影响, 在短时间内的相对定位精度较高.在实时GNSS地震监测和地震波信号提取中, 主要关注的是短时间内相对变化量和振动波形, 因此RTPPP方法非常适合应用于实时GNSS地震仪系统.
GNSS地震仪系统的测量幅度范围没有限制, 只要GNSS接收机能正常工作, 可以测量任意震动幅度的位移.由于实时数据流传输和用户实时轨道钟差产品播发与接收受到网络延迟影响, 该系统的信号输出延时一般为3~5s.而该系统的测量频带范围与GNSS数据采样率有关, 例如, 50Hz采样的GNSS地震仪无法提取频率大于25 Hz的地震信号, 而许多传统地震仪能捕获频率高达几十甚至几百赫兹的地震波信号, 说明GNSS地震仪系统在高频部分的分辨能力与传统地震仪仍有明显差距.因此, 通过实时GNSS地震仪系统获取瞬时地表形变和地震波信号, 再结合传统地震仪记录的地震波加速度和速度数据, 将为地震参数确定和地震快速响应提供更加丰富、可靠的观测资料, 从而实现地震早期预警、海啸预警以及地震灾害快速评估等方面的应用.
| [1] | Blewitt G, Kreemer C, Hammond W C, et al. Rapid determination of earthquake magnitude using GPS for tsunami warning systems. Geophysical Research Letters, 2006, 33(11):L11309, doi:10.1029/2006GL026145. |
| [2] | Crowell B W, Bock Y, Squibb M B. Demonstration of earthquake early warning using total displacement waveforms from Real-time GPS networks. Seismological Research Letters , 80(5): 772-782. DOI:10.1785/gssrl.80.5.772 |
| [3] | Larson K M, Bodin P, Gomberg J. Using 1-Hz GPS data to measure deformations caused by the Denali fault earthquake. Science , 2003, 300(5624): 1421-1424. DOI:10.1126/science.1084531 |
| [4] | Kouba J. Measuring seismic waves induced by large earthquakes with GPS. Studia Geophysica et Geodaetica , 2003, 47(4): 741-755. DOI:10.1023/A:1026390618355 |
| [5] | Bilich A, Cassidy J F, Larson K M. GPS seismology:Application to the 2002Mw7.9 denali fault earthquak.. Bulletin of the Seismological Society of America , 2008, 98(2): 593-606. DOI:10.1785/0120070096 |
| [6] | Shi C, Lou Y, Zhang H, et al. Seismic deformation of the Mw8.0 Wenchuan earthquake from high-rate GPS observations. Advances in Space Research, 2010, 46(2):228-235, doi:10.1016/j.asr.2010.03.006. |
| [7] | Ji C, Larson KM, Tan Y, et al. Slip history of the 2003 San Simeon Earthquake constrained by combining 1-Hz GPS, strong motion, and teleseismic data. Geophysical Research Letters, 2004, 31(17):L17608, doi: 10.1029/2004GL020448. |
| [8] | Miyazaki S I, Larson K M, Choi K, et al. Modeling the rupture process of the 2003 September 25 Tokachi-Oki earthquake using 1-Hz GPS data. Geophys. Res. Lett., 2004, 31(21):L21603, doi:10.1029/2004GL021457. |
| [9] | Avallone A, Marzario M, Cirella A, et al. Very high rate (10 Hz) GPS seismology for moderate-magnitude earthquakes:The case of the Mw6.3 L'Aquila (central Italy) event. Journal of Geophysical Research, 2011, 116:B02305, doi:10.1029/2010JB007834. |
| [10] | Larson K M. GPS seismology. Journal of Geodesy , 2009, 83(3-4): 227-233. DOI:10.1007/s00190-008-0233-x |
| [11] | Geng J, Teferle F N, Meng X, et al. Kinematic precise point positioning at remote marine platforms. GPS Solutions , 2010, 14(4): 343-350. DOI:10.1007/s10291-009-0157-9 |
| [12] | Allen R M, Ziv A. Application of real-time GPS to earthquake early warning. Geophysical Research Letters, 2011, 38(16):L16310, doi:10.1029/2011GL047947. |
| [13] | 张小红, 李星星, 郭斐, 等. 基于服务系统的实时精密单点定位技术及应用研究. 地球物理学报 , 2010, 53(6): 1308–1314. Zhang X H, Li X X, Guo F, et al. Server based real time precise point positioning and its application. Chinese J. Geophys. (in Chinese) , 2010, 53(6): 1308-1314. |
| [14] | Iwabuchi T, Rochen C, Lukes Z, et al. PPP and Network True Real-time 30 sec Estimation of ZTD in Dense and Giant Regional GPS Network and the Application of ZTD for Nowcasting of Heavy Rainfall.//Proceeding of the ION-GNSS, Institute of Navigation, Fort Worth, Texas, 2006:26-29. |
| [15] | Zhang Q, Moore P, Hanley J, et al. Auto-BAHN:Software for near real-time GPS orbit and clock computations. Advances in Space Research , 2007, 39(10): 1531-1538. DOI:10.1016/j.asr.2007.02.062 |
| [16] | 施闯, 楼益栋, 宋伟伟, 等. 广域实时精密定位原型系统及初步结果. 武汉大学学报:信息科学版 , 2009, 34(11): 1271–1274. Shi C, Lou Y D, Song W W, et al. A wide area real-time differential GPS prototype system and the initial results. Geomatics and Information Science of Wuhan University (in Chinese) , 2009, 34(11): 1271-1274. |
| [17] | Shi C, Lou Y D, Song W W, et al. A wide area real-time differential GPS prototype system in China and result analysis. Survey Review , 2011, 43(322): 351-360. DOI:10.1179/003962611X13055561708623 |
| [18] | Boehm J, Niell A, Tregoning P, et al. Global Mapping Function (GMF):A new empirical mapping function based on numerical weather model data. Geophysical Research Letters, 2006, 33(7):L07304, doi:10.1029/2005GL025546. |
| [19] | 方荣新, 施闯, 陈克杰, 等. GPS地震仪:PANDA软件测试结果与验证. 武汉大学学报:信息科学版 , 2011, 36(4): 453–456. Fang R X, Shi C, Chen K J, et al. GPS seismometer:PANDA software testing results and validation. Geomatics and Information Science of Wuhan University (in Chinese) , 2011, 36(4): 453-456. |
| [20] | Bock Y, Melgar D, Crowell B W. Real-time strong-motion broadband displacements from collocated GPS and accelerometers. Bulletin of the Seismological Society of America, 2011, 106(6):2904-2925, doi: 10.1785/0120110007. |
 2013, Vol. 56
2013, Vol. 56