地震是人类一直以来面临威胁最大、破坏性最强的自然灾害, 一旦发生将会对人们的生命财产造成巨大的损失.为减少地震造成的危害, 许多学者不断探索地震监测预报的新方法, 其中地震孕育期电离层扰动与地震电离层耦合机制研究成为地震前兆研究的热点[1-4].自1964年Barnes、Leonard等[5]发现美国阿拉斯加大地震时电离层具有扰动现象以来, 电离层变化与地震的关系逐渐得到各国学者的重视, 并被期望能够用作短临地震的预报.大量的震例和统计分析表明, 大地震在发生的前几天或前几小时, 震区及其附近的电离层中总电子含量(TEC)存在扰动异常, 其特征主要表现在震前10天内电离层TEC有明显的降低趋势[6-12]. Liu等[11]分析了台湾地区1994-1999年期间6.0级以上地震前的电离层F2层临界频率变化, 其结果表明, 地震前1~6天的当地时间12:00-17:00电离层foF2相对其前15天的中值有比较明显的下降, 并将此现象作为一种地震前兆预报地震; Pulinets等[12]通过对十年震前电离层扰动研究的总结, 提出了震前由于地震引起的电离层扰动特征; 孟泱等[8]研究发现在地震发生前的1~4天内电离层TEC普遍减小, VTEC全部低于电离层平静期的平均值; 祝芙英等[13]利用滑动时窗法和四分位距法研究了汶川地震的电离层扰动, 发现电离层TEC异常有向赤道偏移的趋势; 姚宜斌等[14]则利用滑动时窗法分析了2010年全球7个大于7级的地震后发现震前电离层扰动现象并不绝对, 没有统一规律.
在震前电离层异常探测中, 其探测结果准确与否取决于预测参考背景值的精度和背景值误差上下限值的合理性.而目前常用电离层异常探测方法, 如平均值法、中位值法、四分位距法、滑动时窗法等, 虽具有一定的合理性, 但其只考虑了电离层TEC序列的确定性成分, 而未顾及其不确定成分, 因而传统方法预测TEC背景值的精度较低.此外, 传统探测方法在确定参考背景值的上下限值时缺乏合理的统一标准, 且参考背景值的精度较低, 很容易导致探测错误, 而一旦探测错误其将对后续探测结果造成重要影响.
基于此, 本文提出利用时间序列法(ARIMA模型)探测震前电离层TEC扰动异常.首先, 详细比较分析了时间序列法与传统方法在预测电离层TEC参考背景值的精度; 然后, 利用时间序列法以2012年1月10日发生的苏门答腊岛7.2级地震为例进行实例探测分析, 为提高探测结果的准确度, 本文提出了两步探测法, 分析得到了震前13天电离层异常扰动规律和结论, 为电离层异常扰动进行地震短临预报提供参考.
2 异常探测原理及方法 2.1 时间序列(ARIMA模型)探测法 2.1.1 计算参考背景值时间序列法(ARIMA模型)是指采用时间序列分析中的求和自回归移动平均模型对一组有序数据进行观察、研究, 探索预测发展规律.而电离层TEC的变化与地理位置、季节、地方时以及太阳和地磁活动有密切关系, 其TEC值具有明显的年周期变化、季周期变化、日周期变化和随机波动.此序列用时间序列法(ARIMA模型)不但能够较好地顾及其确定性成分, 而且能够计算电离层TEC变化的不确定成分, 以此得到更为准确的电离层参考背景值.
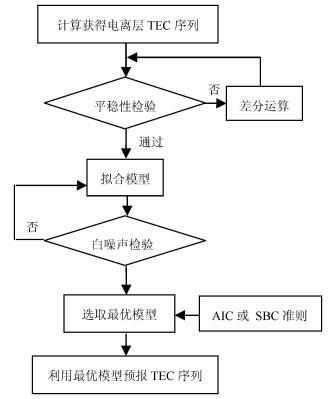
其建模计算电离层参考背景值的过程如图 1所示, 即先用差分法对TEC序列进行平稳化处理, 再对平稳化后的序列构建季节模型, 最后根据AIC和SBC准则找出最优模型后预测得到电离层TEC参考背景值.具体如下, 首先对TEC序列进行以步长为周期长度s的差分运算, 根据观测时序图、观测序列的自相关函数等来判别其周期s, 按(1)式进行季节差分:
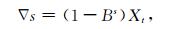
|
(1) |
|
图 1 时间序列法(ARIMA模型)建模计算背景值流程 Fig. 1 Flow chart of modeling and predicting background value using the ARIMA mode |
式中, B为后移算子, X t -s=B sX, 为差分算子, 若经过季节差分后的时间序列仍有趋势, 则再对其进行正常差分 s, 变为序列z(t):
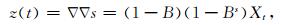
|
(2) |
然后, 对差分后的平稳序列采用ARIMA(求和自回归移动平均)模型进行拟合[15].一般情况下, 经一次季节差分和一次正常差分后, 原序列观测值能够转化为平稳时间序列z(t).若不能, 则继续差分直至为平稳序列.最后, 在建模完成后对模型进行显著性检验, 并对所有通过显著性检验的模型进行AIC准则或SBC准则[16-17]判定, 以此选择最优模型, 并利用最优模型对电离层TEC样本序列进行建模预测得到待探测电离层TEC的参考背景值.
2.1.2 确定探测限值及时间序列法(ARIMA模型)探测流程在震前电离层异常探测中, 除了得到预测参考背景值, 还须得到背景值的合理误差范围.本文利用时间序列法(ARIMA模型)在确定背景值的上下限值时, 提出利用一种更为合理的限值确定策略.首先, 选取距地震较近区域和时期的电离层TEC数据, 且该段数据须不受太阳耀斑、地磁异常等活动的影响.一般此TEC数据的位置最好是震中或者震中附近GIM格网点; 选震前第15至第60天中不受太阳和地磁异常活动影响的28天TEC数据, 由于距发震时间较远, 该数据也不会受地震影响.其次, 利用该段不受异常扰动的前20天正常电离层TEC作为样本数据, 采用时间序列法(ARIMA模型)对其建模预测后8天的参考背景值.最后, 将8天的参考背景值与真实观测值作差, 统计得到所占百分比在95.5%以上的残差值, 以此不受扰动正常期参考背景值的残差值Δ (残差百分比95.5%)作为上下限值, 如式(3)所示:
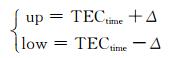
|
(3) |
式中, TECtime为时间序列法(ARIMA模型)预测得到的参考背景值; Δ为利用时间序列法(ARIMA模型)计算得到临近震中区域和时期电离层正常且不受扰动情况下置信度在95.5%以上的残差值; up、low分别为背景范围的上下限值, 超出此范围即为异常扰动.
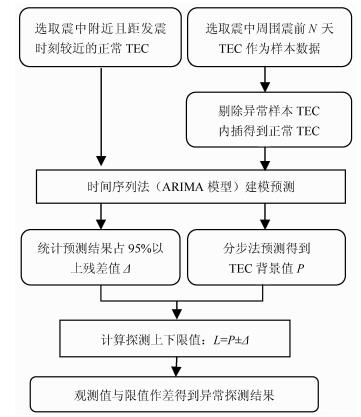
整体电离层异常探测流程如图 2所示, 首先利用上述确定上下限值的方法计算出待探测电离层TEC上下限值.然后, 利用时间序列法建模预测得到震前电离层参考背景值.最后, 利用探测限值和观测值做差得出探测结果.由于时间序列法预测时间越长其结果精度越低, 所以为提高探测结果的准确性, 在预测参考背景值时采用分步预测法, 即每次最长计算7天的参考背景值, 然后样本序列向前滑动(剔除原样本序列最前面的7天数据, 加入刚预测完毕的7天数据组成新的样本序列), 继续向后预测, 直至预测完毕.其中, 新加入的样本数据可能受到地震影响而存在异常, 倘若将异常数据加入到样本序列, 将会对后续预测造成重要影响.因此, 对新加入样本数据中的异常数据进行剔除, 并利用相邻正常数据内插替换该处异常数据, 以保证样本数据长度前后一致.
|
图 2 时间序列法(ARIMA模型)探测TEC异常流程 Fig. 2 Flow chart of anomaly detection using the ARIMA mode |
传统探测电离层异常的方法主要包括中位数法、平均值法、四分位距法和滑动时窗法.中位数法是利用地震发生当月的电离层TEC数据, 将对应时刻的30天TEC数据由小到大排序, 取序列的中位数作为参考背景值, 并计算得到此背景值的标准差, 进而取1.5倍标准差作为参考背景值的限差范围; 平均值法则只与中位数法的背景值取值不同, 是以当月数据对应时刻的平均值做背景值.由于这两种方法均属于静态探测, 它未能剔除样本数据中的异常数据, 而使得计算的背景值与准确值存在很大偏差, 导致探测结果极为不准[13], 所以本文不作对比分析.
四分位距法由台湾国立中央大学的刘正彦教授[11]提出, 该方法综合考虑了中位数法、平均值法的弊端.四分位距法选取待探测时段S天(S能被4整除)的电离层TEC数据, 并将对应时刻S天的TEC数据由小到大排列, 并将其等分为4份, 其等分点依次表示为Q1, Q2, Q3.假设S天对应时刻的数据进行排序后, 得到I1 < I2… < I s, 则Q1, Q2, Q3可表示为式(4), 其上下限值up、low可表示为式(5):
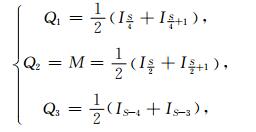
|
(4) |
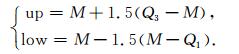
|
(5) |
滑动时窗法也是传统方法中相对合理的一种方法, 它是取适当的滑动时窗长, 计算滑动时窗均值和均方差, 以均值为基值, 以2倍均方差为背景范围.具体如下, 设XL为某站TEC时间序列, 取适当的滑动时窗长N, 由式(6)所示可计算滑动时窗均值XK和均方差σK, 以均值XK为背景参考值, 以2倍σK为参考值的上下限值.
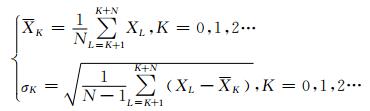
|
(6) |
以上四分位距法和滑动时窗法相比于中位数法和平均数法, 能够较为准确地预测参考背景值, 进而计算较为准确背景参考值的上下限值, 尤其是滑动时窗法能够对异常数据进行实时剔除, 但由于本身预测背景值的精度有限, 所以其探测结果的可靠性不高.
3 时间序列法(ARIMA模型)与传统探测方法的精度比较为了比较时间序列法(AR IMA模型)与传统探测方法预测得到的背景值精度, 并得到运用时间序列方法预测正常TEC序列的合理范围.笔者利用IGS提供的2011年11月22日-12月19日(0°N, 95°E)TEC值序列进行分析, 分别采用传统探测方法(滑动时窗法和四分位距法)和时间序列法(ARIMA模型)对12月12日-19日的背景值进行预测并比较其预测精度.为了考察计算参考背景值的精度, 笔者采用相对精度Prel和绝对精度Pabs{Iave, δ}, 其定义如下式所示.
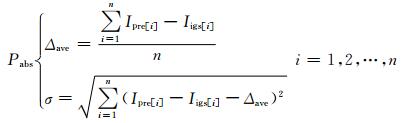
|
(7) |
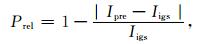
|
(8) |
式中, Δave为预报值与真值的平均残差; σ为预报残差的中误差; Ipre为预报的电离层TEC值; Iigs为IGS发布的TEC观测值; n为预报的数据量.
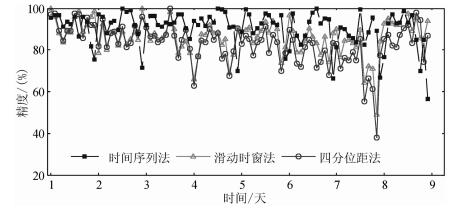
图 3给出了时间序列分析方法、滑动时窗法和四分位距法预测2011年12月12日-19日8天的相对精度对比图.由图 3可以看出, 时间序列法(ARIMA模型)预测TEC序列的相对精度最高, 其次是滑动时窗法和四分位距法.虽然预测初期背景值的精度相当, 但是随着时间的增加时间序列法要明显优于传统探测方法. 图 3中出现规律性的低精度历元, 这是由于时间序列法(ARIMA模型)在预测电离层TEC序列极值时存在一定缺陷, 但其结果并不太差.
|
图 3 时间序列法与传统方法预测背景值相对精度对比图 Fig. 3 Comparison Figure of Relative Prediction Accuracy of Time Series Method and Traditional Methods |
表 1为三种探测方法每天的绝对精度和相对精度统计, 相对精度的结论与图 3一致.从绝对精度来看, 时间序列法(ARIMA模型)预测背景值的平均偏差Δave要明显优于其他传统探测方法的, 虽然其标准偏差σ要稍差, 但三者相差不大.可以看出, 滑动时窗法和四分位距法预测得到的背景值存在很大的系统性偏差, 而此系统性偏差将对电离层异常探测造成巨大影响, 即使限差范围取值再合理, 也不一定得到准确的探测结果.
|
|
表 1 三种方法预测的精度统计 Table 1 The predicted values' absolute accuracy and relative accuracy of the three methods |
表 2为三种探测方法预报参考值的残差统计, 其中, Δ表示预报残差绝对值.由表 2可知, 时间序列法(ARIMA模型)、滑动时窗法、四分位距法预报残差小于6.2TECu分别占到90.62%、63.54%和51.04%, 时间序列法预报残差小于3TECu所占百分比也是其他两种传统方法的两倍多.由表 2还可看出, 时间序列法的预测残差要明显小于传统探测方法的结果.
|
|
表 2 三种方法预报残差分类百分比统计 Table 2 Category percentage of predicted residuals of the three methods |
上述从不同方面对比分析了时间序列法(ARIMA模型)与传统探测方法的预测精度,实验结果表明时间序列法(ARIMA模型)的精度远高于传统方法.
因此, 利用时间序列法(ARIMA模型)来预测正常TEC序列参考背景值更为合理.同时, 也能得出一个较为合理的背景值误差范围.
4 苏门答腊岛7.2级地震电离层异常探测实例 4.1 数据选取及处理策略选取2012年1月10日18时36分(当地时间2012年1月11日凌晨1时36分)发生在苏门答腊岛的7.2级地震(震中2.4°N、93.2°E, 震深19km)作为研究对象, 研究其震前13天及震后1天的电离层扰动情况, 电离层TEC数据采用IGS提供的电离层GIM格网产品.
探测过程主要依据本文2.1节提出的流程进行处理.首先, 将2011年12月9日到28日连续20日的电离层TEC数据作为样本序列, 预测2011年12月29日到2012年1月4日(即震前第13天到第7天)的TEC参考背景值.然后, 根据2.1.2节中限值确定策略计算探测限值, 由于本文3.1节已经分析得到了2011年12月12日到19日时间序列法预报参考值误差统计表(如表 2所示), 且该数据距发震时间和震中较近, 同时不受太阳、地磁、地震等活动影响, 因此所占比例在95.5%以上的预报残差值(±8.2TECu)可以作为此震震前电离层探测时预测背景值的误差范围.最后, 根据2.1节中所介绍的异常探测原理, 笔者对该实例采用两步法进行探测.即先探测震前第13天至第7天电离层异常情况, 然后, 在预测剩余7天时, 将20天样本数据向前滑动7天, 即剔除20天样本序列前7天的数据, 再将震前第13天到第7天的数据加入到样本序列.而对新加入的样本序列进行异常剔除, 并利用相邻内插法计算正常值将其替换.
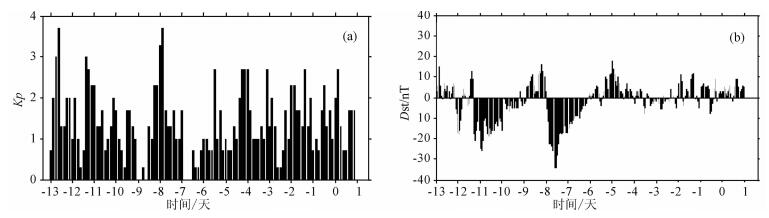
为了表明2012年1月10日苏门答腊7.2地震震前13天电离层异常与太阳、地磁异常活动和天气变化等地无必然联系. 图 4给出了震前13天各时段表征地磁活动的Kp指数和其附近地磁台站发布的表征环电流强度的Dst指数.一般认为, Kp指数小于3电离层是比较安静的; Dst指数低于-50nT时, 表示中级磁暴可能发生, 当Dst指数在-100n T以下时, 有可能发生大磁暴.由图 4所示结果可知, 地震期间Kp指数和Dst指数处于较低的水平, 因此可以排除该地震震前13天和震后1天电离层受太阳活动、磁暴等空间活动的影响, 如果探测出电离层异常, 那么就可以认为这段时间的电离层异常极有可能是由地震活动引起的.
|
图 4 震前(2011年12月29日到2012年1月11日)探测时段Kp指数和Dst指数图 Fig. 4 Probing period′s Kp and Dst index before the earthquake (from Dec 29th, 2011 to Jan 11th, 2012) |
笔者分析了震中附近周围4个GIM格网点震前13天及震后1天共14天的电离层TEC异常情况, 其结果如图 5所示.其中, 图 5中的(a)、(b)、(c)、(d)四幅分图分别为震中东北向(EN)、西北向(WN)、东南向(ES)、西南向(WS)4个GIM格网点的探测结果(左图为时间序列法结果; 右图为滑动时窗法结果), 其每幅分图分两部分, 上半图为异常探测序列图, 蓝色点线为异常限值, 红色点线为实际观测值; 下半图则为真实观测值超出正常值限值的差值, 其红色柱状为正异常, 即观测值高于上限, 而蓝色柱状表示负异常, 即观测值低于下限.

|
图 5 时间序列法(左图)与滑动时窗法(右图)震前TEC异常探测结果图 Fig. 5 The results figure of TEC anomaly detection using ARIMA model (left) and IQR method (right) |
由图 5可以看出, 时间序列法和滑动时窗法的探测结果存在较大差异, 尤其是滑动时窗法的探测结果发生异常的天数要明显多于时间序列法, 而且一旦出现异常, 随后数天都有异常发生, 同时正负异常并没有一定规律.这与滑动时窗探测法存在的缺陷有关, 即其预报的参考背景值精度较低且其误差限值取值不合理, 这也是造成目前传统方法研究震前电离层扰动异常结果不一的原因.
由于滑动时窗法探测结果可信度和准确度存在一定问题, 因此, 本文只对时间序列法探测结果的电离层异常规律做详细分析.从图 5中的时间序列法(AR IMA模型)探测结果可知, D1点(东北向)在震前第13天出现较明显的正异常, 震前第9~10天发生负异常, 而D2点(西北向)和D1点(东北向)异常情况基本一致. D3点(东南向)震前第9天、第1~2天以及地震当天发生明显负异常, D4点(西南向)异常情况与D3基本一致.由表 3综合统计了地震震中四个方向发生异常情况(1表示正异常, -1表示负异常).可以看出, 只在震前第13天在震中以北发生较为明显的正异常, 以南方向正异常则未发生.而负异常在震中周围的四个方向均会发生负异常, 且一般发生于震前第9~10天、第1~2天和地震当天.结合图 5发现, 震中以北较容易发生明显正异常, 且距发震时间相对较远; 而负异常则在震中以南发生的较为明显, 且负异常距发震时间相对较近.
|
|
表 3 震前各方向异常统计结果 Table 3 Anomalies statistical results in all directions before and when the earthquake happened |
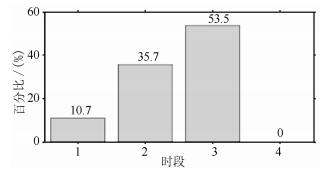
为了更充分地了解地震异常发生的规律, 笔者对所有异常进行分时段统计, 给出了在不同时段异常发生的频率, 其结果如图 6所示.其中, 1、2、3、4分别代表一天中的四个时段, 即GMT 0:00-6:00 (LT 7:00-13:00)、GMT 6:00-12:00 (LT 13:00-19:00)、GMT 12:00-18:00(LT 19:00至次日1:00)、GMT 18:00-24:00(LT次日1:00至次日7:00), GMT为国际时, LT为地方时.由图 6可知, 第1、2、3时段异常发生的频率逐渐增大, 而且在第4时段发生异常的频率则最低.对比发震时刻(GMT 18:36)可以发现, 时段3是离发震时刻前最近的时段, 而时段4则是离发震时刻后最近的时段; 结合发震时刻前的第1时段和第2时段可以发现, 在发震时刻前, 离发震时刻越近的时段其异常发生的频率越高; 而在发震时刻后, 离发震时刻最近的第4时段则发生异常的频率最小.对发生异常频率最高的第3时段(GMT 12:00-18:00)分析可知, 该时段处于当地时间19:00至次日凌晨1:00, 并未受到过多太阳活动的影响.因此, 上述规律很有可能与地震有关, 由于分析震例有限, 该规律尚待进一步研究.倘若存在此规律, 将会对未来预报发震时间(准确到时段)提供重要的参考价值.
|
图 6 各时段发生异常百分比统计图 Fig. 6 Percentage of anomalies occurred in each period |
本文提出了利用时间序列法(ARIMA模型)进行震前电离层异常探测的新方法, 详细介绍了该方法的探测原理及流程, 并分析对比了与其他传统探测方法的不同点和预测背景值的精度.结果表明, 时间序列法(ARIMA模型)预测背景值的精度要明显优于四分位距法和滑动时窗法, 特别是传统方法的预测结果存在较大系统偏差, 该缺陷将会对后续电离层异常探测造成重要影响.此外, 针对传统方法在确定上下限值方面存在缺陷的问题, 本文给出了一种较为合理的限值确定策略, 由此利用高精度的背景值和合理的上下限值所探测出异常结果和得出的结论则更加合理.最后, 本文利用时间序列法(ARIMA模型)分析了2012年1月10日的苏门答腊岛7.2级大地震震前电离层TEC扰动情况, 得出以下结论:
(1) 苏门答腊大地震震前13天及震后1天确实存在明显的电离层异常现象, 且该异常现象并不受太阳活动、地磁活动等外界空间影响.因此, 可以表明地震震前会一定程度上导致电离层异常扰动, 利用震前电离层异常扰动现象有可能成为地震短临预报的一种手段.
(2) 从苏门答腊大地震震前电离层异常规律来看, 电离层异常会发生在震前第13天、第8~9天、第1~2天和震前数小时.其中, 正异常主要发生在震中以北, 而且距发震时间较远, 而震中以南正异常并不明显; 负异常主要集中在震前数天以及震前8~4h, 而且四个方向均存在, 且距发震时间较远.
(3) 通过对异常结果分时段统计发现, 在发震时刻前距发震时刻越近的时段发生异常的频率越高, 而在发震时刻后距发震时刻越近的时段其发生异常的频率则越低.由于分析震例有限, 该规律尚待进一步研究.倘若存在此规律, 将会对未来更为准确的预报发震时间(准确到时段)提供重要参考.
运用更加准确的TEC异常探测方法通过实例证实震前电离层扰动现象确实存在, 表明利用电离层扰动现象预报地震具有其可行性.但是由于地震机理的复杂以及震前电离层扰动的物理机制不明, 利用电离层扰动预报短临地震还需要进一步研究.
致谢衷心感谢IGS、美国NGDC、日本京都地磁中心为本文分别提供的电离层TEC数据、Kp指数和Dst指数.
| [1] | Astafyeva E, Heki K. Vertical TEC over seismically active region during low solar activity. J. Atmos. Sol.-Terr. Phys. , 2011, 73(11): 1643-1652. |
| [2] | Chavez O, Pérez-Enríquez R, Cruz-Abeyro J A, et al. Detection of electromagnetic anomalies of three earthquakes in Mexico with an improved statistical method. Nat. Hazards Earth Syst. Sci., 2011, 11:2021-2027, doi:10.5194/nhess-11-2021-2011. http://www.oalib.com/paper/1378483 |
| [3] | Hasbi A M, Mohd Ali M A, Misran N. Ionospheric variations before some large earthquakes over Sumatra. Nat. Hazards Earth Syst. Sci., 2011, 11:597-611, doi:10.5194/nhess-11-597-2011. http://www.oalib.com/paper/2537043 |
| [4] | Oyama K I, Kakinami Y, Liu J Y, et al. Reduction of electron temperature in low latitude ionosphere at 600 km before and after large earthquakes. J. Geophys. Res., 2008113:A11317, doi:10.1029/2008ja013367. http://onlinelibrary.wiley.com/doi/10.1029/2008JA013367/full |
| [5] | Barnes R A, Leonard R S. Observations of ionospheric disturbances following the Alaska earthquake. J. Geophys. Res. , 1965, 70: 1250-1253. DOI:10.1029/JZ070i005p01250 |
| [6] | Pulinets S A, Contreras A L, Ciraolo L, et al. Total electron content variations in the ionosphere before the Colima, Mexico, earthquake of 21 January 2003. Geofisica Internacional , 2005, 44(4): 369-377. |
| [7] | Datchenko E A, Ulomov V I, Chernyshova C P. Electron density anomalies as the possible precursor of Tashkent earthquake. Dokl. Uzbek. Acad. Sci. , 1972, 12: 30-34. |
| [8] | 孟泱, 王泽民, 鄂栋臣. 基于GPS数据的地震前电离层TEC异常研究. 武汉大学学报(信息科学版) , 2008, 33(1): 81–84. Meng Y, Wang Z M, E D C. Ionopsheric TEC anomalies of pre-earthquake based on GPS data. Geomatics and Information Science of Wuhan University (in Chinese) , 2008, 33(1): 81-84. |
| [9] | 林剑, 吴云, 祝芙英, 等. 基于GPS探测汶川地震电离层TEC的异常. 地球物理学报 , 2009, 52(1): 297–300. Lin J, Wu Y, Zhu F Y, et al. Wenchuan earthquake ionosphere TEC anomaly detected by GPS. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 297-300. |
| [10] | 蔡军涛, 陈小斌, 赵国泽, 等. 地震前兆:电离层F2层异常. 地球物理学进展 , 2007, 22(3): 720–728. Cai J T, Chen X B, Zhao G Z, et al. Earthquake precursor:the anomalies in anomalies in the ionospheric F2 region. Progress in Geophysics (in Chinese) , 2007, 22(3): 720-728. |
| [11] | Liu J Y, Chen Y I, Pulinets S A, et al. Seismo-ionospheric signatures prior to M≥60 Taiwan earthquakes. Geophys. Res. Lett. , 2000, 27(19): 3113-3116. DOI:10.1029/2000GL011395 |
| [12] | Pulinets S A, Legen'ka A D, Gaivoronskaya T V. Main phenomenological features of ionospheric precursors of strong earthquakes. Atmos. Sol. Terr. Phys. , 2003, 65: 1337-1347. DOI:10.1016/j.jastp.2003.07.011 |
| [13] | 祝芙英, 吴云, 林剑, 等. 汶川Ms8.0地震前电离层TEC异常分析. 大地测量与地球动力学 , 2008, 28(6): 16–21. Zhu F Y, Wu Y, Lin J, et al. Study on ionospheric TEC anomaly prior to Wenchuan Ms8.0 earthquake. Journal of Geodesy and Geodynamics(in Chinese) (in Chinese) , 2008, 28(6): 16-21. |
| [14] | Yao Y B, Chen P, Zhang S, et al. Analysis of pre-earthquake ionospheric anomalies before the global M=7.0+earthquakes in 2010. Nat. Hazards Earth Syst. Sci , 2012, 12: 575-585. DOI:10.5194/nhess-12-575-2012 |
| [15] | James D. Hamilton. Time series Analysis. Time series Analysis, 1994 . |
| [16] | 王燕. 应用时间序列分析. (第二版). 北京: 中国人民大学出版社, 2008 . Wang Y. Application of Time Series Analysis (in Chinese). (The second edition). Beijing: People's University of China Press, 2008 . |
| [17] | 何书元. 应用时间序列分析. 北京: 北京大学出版社, 2007 . He S Y. Application of time series analysis (in Chinese). Beijing: Beijing University Press, 2007 . |
 2013, Vol. 56
2013, Vol. 56

