2. 中国科学院寒区旱区环境与工程研究所, 寒旱区陆面过程与气候变化重点实验室, 兰州 730000;
3. 甘肃省气象信息与技术装备保障中心, 兰州 730020
2. Key Laboratory of Land Surface Process and Climate Change in Cold and Arid Regions, Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China;
3. Gansu Meteorological Information and Technical Equip Safeguard Center, Lanzhou 730020, China
蒸发皿作为一种直接监测大气蒸发能力的工具, 被广泛应用于水文、气象、农业等领域[1-2].中国在常规观测中有E601B蒸发皿(直径62cm)和20cm蒸发皿(直径20cm)两种类型, 分别在非冻结和冻结情况下使用.分析过去数十年蒸发皿蒸发量(Epan)资料表明, 全球多个区域Epan呈明显下降趋势, 但对造成这一下降趋势的解释却并不统一.认为导致Epan下降的主要原因有云和气溶胶的增加导致太阳辐射减少造成的[3-4], 也有研究认为是地面蒸发加强导致空气湿度增加造成的[5-6], 还有研究认为是风速减小所致[7].甚至于在以蒸发皿蒸发量进行气候分析时得出地气系统中循环是加速[5, 8]和减速[3, 9]两种截然相反的结论.对Epan相关的气候分析存在如此不确定的原因, 主要是不能准确地描述蒸发皿蒸发的物理过程以及多种环境因子在蒸发过程中的非线性相互作用, 其次, 研究方法多为统计分析或者经验模型, 这样难以定量分析各环境因子对Epan的贡献[10-11].
有关蒸发皿蒸发量的经验模型建立在统计分析的基础之上, 大多通过改进计算潜在蒸发的Penman-Monteith模型[12]发展而来[13-15], 这些模型多以日平均或更长时间尺度的气象变量为输入量, 因此很难详细地揭示Epan的日变化特征和蒸发皿蒸发的微物理过程.始于20世纪末针对蒸发皿蒸发量进行了数学物理模式研究, 研究注重于蒸发的物理过程. Jacobs[16]和Martinez [17]通过设置野外试验构建蒸发皿蒸发模型, 分别研究水温和Epan的日变化过程.在Jacobs和Martinez的模型中, 他们认为水面感热和潜热通量是由蒸发皿水面自身生成的湍流所决定的, 并没有考虑局地环境与水面所构成的非均匀下垫面对水面湍流的影响, 且感热和潜热输送系数使用由风速线性拟合的经验函数, 这些经验结论忽略了大气层结对湍流传输系数的影响[18]. Chu借助风洞实验对Penman-Monteith型蒸发皿经验模型进行修正[19], 风洞实验只考虑了动力因子对湍流的影响, 没有考虑热力因子对湍流发展和维持所起的重要作用, 但实况中湍流是由热力和动力共同制约的[20], 实际蒸发皿蒸发远比风洞实验室的复杂, 因此该模型也存在一定的局限性.
迄今为止, 近地层观测已取得了长足进步.同时蒸发皿的蒸发过程就处在近地层, 应用近地层丰富的观测资料研究蒸发皿蒸发有利于揭示蒸发皿蒸发的微物理过程.本研究通过设计野外试验, 以能量平衡原理和边界层梯度输送理论为基础[21-23], 借助陆面过程研究成果[24], 考虑蒸发皿水面与周围下垫面之间的非均匀相互作用, 利用微气象观测量, 建立高时间分辨率的(1h)20cm蒸发皿蒸发模型.该研究有利于通过数值方法揭示20cm蒸发皿蒸发的物理意义和定量分析各气象因子在蒸发皿蒸发中的作用, 进一步可以利用数值方法寻求导致气象观测的蒸发皿蒸发量显著减小的根本原因, 揭示蒸发皿蒸发量变化所给出的气候变化信号.另外, 基于能量平衡原理建立的数值模型普适性比较强, 比较容易推广到更大尺度的水体蒸发模拟研究, 如较大尺度的蒸发皿、蒸发池和小水域的蒸发过程模拟.
2 试验设置和数据介绍"古浪非均匀近地层观测试验"(Gulang Heterogeneous UnderlyingSurfaceLayerExperiment, GHUSLE)位于中国甘肃省武威市古浪县海子镇东新村, 试验场地经纬度范围: 37°37′N-37°38′N, 103°48′E-103°51′E, 试验时间: 2010年5月20日-7月15日. GHUSLE沿东西剖面在不同下垫面(沙漠-绿洲-沙漠)上设置了三个气象观测站, 分别为西沙漠、农田和东沙漠站, 试验详细介绍见文献[25].
蒸发皿蒸发试验设在试验场西端的西沙漠站点(37°37. 921′N, 103°48. 011′E), 海拔高度为1637m, 该站点位于腾格里沙漠与绿洲的过渡带上, 站点下垫面为活动小沙丘, 蒸发皿试验时间: 6月26日-7月15日.蒸发皿选用标准中国式20cm蒸发皿(ADM7, 天津气象仪器厂), 蒸发皿放置在一个高为20cm的空心预制砖上.观测方法为每日08: 00(为北京时, 地方时比北京时晚约1h, 下同)将蒸发皿中水体补充到3200g(蒸发皿和水共重3200g, 其中蒸发皿重1770g), 蒸发皿水温(Tw)和蒸发量观测时间间隔均为1h.温度观测用红外测温仪(精度为0. 2 ℃), 蒸发皿蒸发量和蒸发通量的观测用称重法, 仪器为电子秤(精度为1g).将观测的蒸发皿每小时重量差折算为蒸发皿单位面积、单位时间所对应的蒸发量Epan(kg·m-2·s-1)(即蒸发皿蒸发通量), 蒸发通量乘以水的汽化潜热系数λ(=2. 45× 106J·kg-1, 20℃), 即为蒸发皿的潜热通量λEpan (W·m-2).微气象观测量包括近地面风速、气温、空气湿度、气压, 仪器架设高度均为2 m, 风向观测高度为2. 5 m; 辐射用四分量净辐射仪(CNR4, Kipp & Zonen)测量, 仪器架设高度为1. 5m;湍流特征量通过三维超声风速仪(CSAT3, Campbell)和CO2/H2O开路气体分析仪(Li7500, Li-Cor)测量, 仪器架设高度为2. 5m; 5层土壤地温、地湿测量系统, 深度分别为: 5cm、10cm、20cm、40cm和80cm; 2层土壤热流板, 深度分别为5cm和10cm.
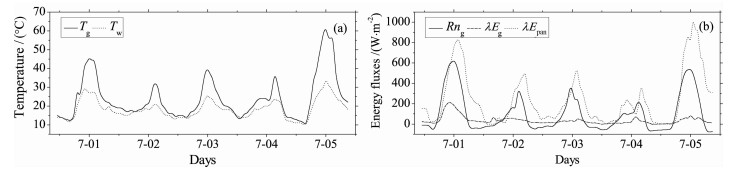
3 蒸发皿蒸发量观测事实及其物理数学模型构建 3.1 蒸发皿蒸发量观测事实蒸发皿水面与周围地表温度观测表明, 两者之间存在显著的差异, 7月1-5日观测的蒸发皿水面温度Tw与周围地表温度Tg的对比显示(图 1a), 除凌晨时分Tw与Tg大小相当外, 其余时段Tw一致小于Tg.日出时刻(07: 00时)为各自当日最低值, 正午时分(13: 00时)分别达到各自当日最大值, 两者温差存在明显的日变化, 最大温差出现在正午时分.受天气条件的影响, 晴天Tw和Tg分别在10~30 ℃和10~60 ℃之间变化, 两者最大差值达到30℃(7月5日); 阴天Tw和Tg的日变化幅度较小, 分别在10~20℃和10~30℃之间变化, 且两者最大差值约为10 ℃.
|
图 1 地表与蒸发皿水面观测量对比 (a)温度; (b)能量通量. Fig. 1 Comparison of measurements between land and pan water surfaces (a)Temperature; (b)Energy fluxes. |
蒸发皿水面与周围地表之间的蒸发通量观测显示, 主要受蒸发水源的影响, 即周围下垫面没有充足的水分用于蒸发, 导致水面潜热通量λEpan远大于地面潜热通量λEg(图 1b), 在典型晴天λEpan和λEg的差值最大可达到900 W·m-2(7月5日), 阴天这一差值较小, 约为300 W·m-2. λEpan的日较差主要受天气条件的影响, 在典型晴天能达到1000 W·m-2 (7月5日), 而阴天λEpan的日较差却只有400W·m-2左右.从图 1b可见, λEpan的变化主要受到蒸发皿可利用能量的限制; 而λEg则主要受土壤可蒸发水量的控制.除7月1日因前一天发生降水影响, 土壤中可蒸发水量较大, λEg最大值达到了200 W·m-2外, 其余时段λEg均在0~50 W·m-2之间变化, 且随着土壤变得"越来越干", 可蒸发水量减小, λEg也逐渐变小.
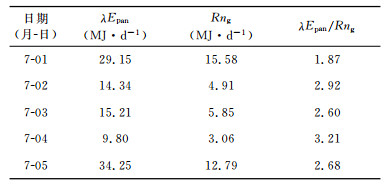
地表净辐射Rng与蒸发皿蒸发潜热通量λEpan的对比分析显示(图 1b), 除清晨到中午个别时段Rng略大于λEpan外, 其余时段Rng均小于λEpan.两者最大差值同样因天气条件的变化而不同, 阴天最大差值约200 W·m-2(7月2-4日), 晴天这一差值将超过400 W·m-2(7月5日).为了更进一步定量比较Rng与λEpan之间的大小关系, 将两者的日积分总量进行比较(表 1).连续5天, 两者日总量比较结果为λEpan明显大于Rng, 两者比值(λEpan/Rng)的最大值达3. 21(7月4日), 最小值为1. 87(7月1日), 5天的平均值为2. 70.这表明蒸发皿蒸发所消耗的能量远大于周围环境的净辐射能.因此, 只有合理地估计蒸发皿蒸发过程中从周围环境得到的所有能量, 正确分析不同能量对蒸发皿蒸发的作用过程, 才能准确地计算蒸发皿蒸发量以及揭示蒸发皿蒸发量所代表的物理意义.
|
|
表 1 地表净辐射与蒸发皿水面潜热通量 Table 1 Land surface net radiation and pan water surface latent heat flux |
蒸发皿是直接观测大气综合蒸发能力的常规仪器.有关其蒸发的物理过程和特殊性, 左洪超已进行了详细的论述[11], 明确指出蒸发皿水面与周围地表之间构成显著的非均匀性.由于这种非均匀性使得蒸发皿与土壤、大气之间存在着复杂的能量交换过程, 对于大型水面、小型水面、Class A蒸发皿和20cm蒸发皿, 其复杂性也是逐级递增的.蒸发皿中水蒸发包括水挥发和水汽扩散两个过程, 环境中任何影响这两个过程的因子变化都可以影响蒸发皿的蒸发量, 但是整个蒸发过程都要受到能量守恒的制约, 因此从能量的角度研究蒸发皿蒸发具有更大优势.
结合图 2可以给出蒸发皿蒸发的物理模型.在蒸发皿所处的沙漠下垫面上, 受土壤水分的影响, 地表感热Hsg远大于潜热λEg; 而在蒸发皿水面, 感热Hsw却远小于潜热λEpan; 同时, 水面温度Tw也小于地表温度Tg.这种巨大差异构成了地表和蒸发皿之间的非均匀性, 从而导致驱使蒸发皿蒸发的能量不仅仅为水面净辐射(Rnw), 还包括来自周围较"热"下垫面上的能量输送, 并且对于20cm蒸发皿该能量输送尤为明显.这种能量输送包括两方面:其一为平流感热, 部分Hsg平流到蒸发皿上方, 在湍流的垂直交换作用下, 被水面吸收, 从而增加了驱使蒸发皿蒸发的能量来源.这一平流能量的大小不仅与Hsg和Hsw的差异有关, 同时与湍流的垂直交换速率也有关. Hsg和Hsw两者的差异越大, 且垂直交换越强, 其平流感热能对蒸发提供的能量也就越多, 这也正是沙漠中蒸发皿蒸发量远大于绿洲中的主要原因.其二为侧壁发生的能量交换通量Ht, 对于20cm蒸发皿, 其侧壁面积约为上表面的2倍, 当Tg和Tw差异较大时, Ht对蒸发皿蒸发强度的影响也越大.因此, 如何正确参数化蒸发皿接受的输送能量是精确模拟蒸发皿蒸发量的关键问题.

|
图 2 20 cm蒸发皿与环境之间能量平衡和相互作用 Fig. 2 Energy balance and interaction between 20 cm evaporation pan and local environment |
在上述物理模型的基础上, 以能量守恒为基础建立20cm蒸发皿蒸发的数学模型.该模型可以表示为
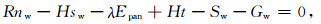
|
(1) |
其中, Rnw为水面净辐射(W·m-2), Hsw和λEpan分别为水面感热、潜热通量(W·m-2), Ht为蒸发皿侧壁与周围环境之间的能量交换通量(W·m-2), Sw为蒸发皿中水体热存储功率(W·m-2)(Sw为正值表示水体吸收能量, 负值表示释放能量), Gw为蒸发皿底部热通量(W·m-2).
水面净辐射Rnw表示为
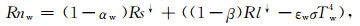
|
(2) |
其中, Rs↓为向下短波辐射(W·m-2), αw为水面反照率(这里忽略αw随太阳高度角的变化, 取αw=0. 03, 文献[20]), Rl↓为向下长波辐射(W·m-2), β为水面长波反射系数(取β=0. 03, 文献[20]), εw为水面长波发射系数(取εw=0. 97, 文献[20]), σ为Stefan-Bolzmann常数, Tw为蒸发皿水面温度(K).
利用边界层理论中的梯度输送理论, 水面感、潜热通量Hsw、λEpan可以分别表示为

|
(3) |
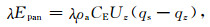
|
(4) |
其中, ρa为空气密度(kg·m-3), cp为空气定压比热(J·kg-1K-1), Uz和Tz分别为z高度处水平风速(m·s-1)和空气温度(K), Tw为水面温度(K), λ为水相变潜热常数(J·kg-1), CH和CE分别为水面感、潜热输送系数, qs表示温度为Tw的饱和水汽压es所对应的空气比湿(kg·kg-1), qz为z高度处空气比湿(kg·kg-1), qs和qz用以下方法计算:
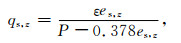
|
(5) |
其中, ε为常数(ε=0. 622), es和ez分别表示水面饱和水汽压和z高度处水汽压(hPa), P为大气压强(hPa), 水面饱和水汽压es可用水面温度Tw表示为
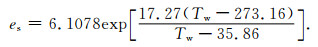
|
(6) |
在利用蒸发皿进行观测时, 由于蒸发皿尺寸远小于周围环境, 可以认为蒸发皿对局地环境的动力、热力以及水汽过程的影响很小, 于是近似认为蒸发皿所处下垫面同周围环境下垫面的地气相互作用特征完全相同.因此主导蒸发皿水面感、潜热输送的湍流特征主要由周围环境所决定.在计算蒸发皿水面的感、潜热通量时, 具体做法如下, 用超声风速仪(架设高度为2. 5m)来确定周围环境下垫面上湍流输送系数; 之后利用计算的湍流输送系数, 依据梯度输送理论(公式(3)、(4))计算蒸发皿水面的感、潜热通量.
应用Monin-Obukhov相似理论, 感热和潜热输送系数CH和CE表示如下[22]:
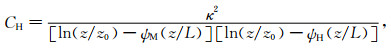
|
(7) |
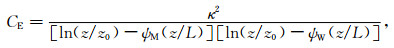
|
(8) |
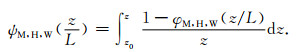
|
(9) |
利用Dyer试验结论,
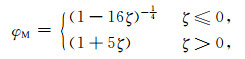
|
(10) |
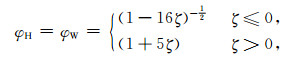
|
(11) |
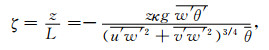
|
(12) |
其中, ψM、ψH和ψW分别为Monin-Obukhov相似性普适函数φM、φH和φW的积分形式, z为物理量观测高度(m)(z=2. 50m), z0为粗糙度长度(m)(z0=0. 017 m), L为Monin-Obukhov长度(m), ζ为Monin-Obukhov大气稳定度参数, 并且ζ=z/L, κ为V. Karman常数, g为重力加速度, w′θ′是感热通量, u′w′和v′w′分别为u和v方向的动量通量, θ为平均位温.
在蒸发皿与周围环境构成的极端非均匀下垫面上, 水面与地表热力性质的不同使水温和地表温度之间存在较大的差异, 导致蒸发皿侧壁和环境之间发生能量交换, 将这一能量交换视为侧壁接收和发射的长波辐射通量差, 发射的长波辐射通量以水体特征来估计(蒸发皿导热性能良好, 认为蒸发皿侧壁与水温相等), 吸收的长波辐射通量用地表向上发射的长波辐射通量Rl↑来近似[14].再将这一通量差等效到垂直方向, 于是蒸发皿侧壁热通量Ht表示为

|
(13) |
其中, Spana和Spanu分别为蒸发皿侧壁面积和上表面积(m2)(Spana=0. 20π·δz, Spanu=(0. 10)2π, δz为蒸发皿中水深度(m), δz=M/(Spanu ·ρw), M为水的质量(kg)).
蒸发皿水体热贮藏率Sw表示为
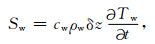
|
(14) |
其中, cw为水比热(J·kg-1·K-1), ρw为水密度(kg·m-3), ∂Tw/∂t为水温随时间的变化率.蒸发皿中水体深度较小, 在热传导和对流作用下, 水体温度层结可以忽略(Martinez, 文献[18]), 认为整个水体是等温的.
蒸发皿底部热通量Gw没有观测, 通常Gw很小, 为了简化模型, 这里设Gw=0.
3.4 数值计算方法在20cm蒸发皿数学物理模型(方程(1))中代入相应的各分量, 则方程(1)转化为水温Tw随时间t的一阶常微分方程, 给定方程初始条件, 便构成如下定界问题:
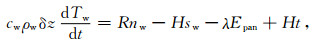
|
(15) |
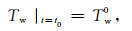
|
(16) |
其中, Tw0为Tw的初始值.
应用隐式Euler法对方程(15)离散得到
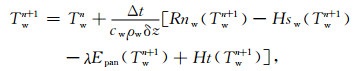
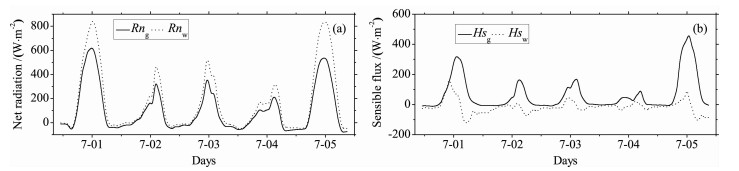
|
(17) |
其中, Twn和Tn+1 w分别表示n和n+1时刻的水温, Δt为时间步长.利用牛顿迭代法求解方程(17)得到n+1时刻的水温Tn+1 w, 同时也解得n+1时刻的其它相关各分量, 如蒸发皿水面净辐射Rnw(Tn+1 w)、感热通量Hsw(Tn+1 w)和潜热通量λEpan(Tn+1 w)等, 进而得到蒸发皿蒸发通量Epan(kg·m-2·s-1).通常用蒸发皿蒸发的绝对水深单位毫米(mm)来表示某一时段的蒸发皿蒸发量, 因此Epan的单位也可转化为(mm·s-1)(如Epan(mm·s-1)=1000(mm·m-1)× Epan(kg·m-2·s-1)/1000(kg·m-3), 其中1000 (kg·m-3)为水密度).对每小时内的Epan(mm·s-1)进行时间积分便得到对应的蒸发皿每小时蒸发量Epan(mm· h-1).
模型输入强迫量为5min平均的微气象观测数据: Rs↓、Rl↓、Rl↑、U2. 0、Ta、Rh、P、u′w′、v′w′和w′θ′.每日08: 00时对水体质量M0和温度T0分别赋初值, 然后向后积分24h, 积分时间步长为5min.
4 数值结果分析 4.1 蒸发皿水面净辐射和感热模拟试验结果表明, 蒸发皿水面温度Tw、潜热通量λEpan与周围地表温度Tg、潜热通量λEg之间存在显著的差异(图 1), 蒸发皿小水面与周围地表构成极端非均匀下垫面.由于蒸发皿小水面的特殊性, 除了温度和蒸发量可以直接观测外, 水面净辐射Rnw和感热通量Hsw观测比较困难.利用所建立的20cm蒸发皿蒸发模型对Rnw和Hsw进行模拟, 蒸发皿水面模拟值与周围地表观测值的比较如图 3所示. 图 3a为观测的地表净辐射Rng与模拟的水面净辐射Rnw的比较, 连续5天的比较结果显示, Rnw一致大于Rng, 两者最大差值随天气条件而不同, 晴天约为200 W·m-2, 阴天约为100 W·m-2.这一差异主要是两种下垫面之间反照率和温度的不同所造成的, 水面反照率小于地表反照率, 因此地表反射短波辐射大于水面的; 另外, 白天地表温度大于水面温度, 使得地表向上的长波辐射大于水面的, 地面净长波辐射小于水面的, 从而导致Rnw明显大于Rng.
|
图 3 地表观测量与蒸发皿水面模拟量对比 (a)净辐射; (b)感热通量. Fig. 3 Comparison the land surface measurements and the pan water surface simulation (a)Net radiation; (b)Sensible flux. |
观测的地表感热通量Hsg与模拟的水面感热通量Hsw的比较如图 3b所示, Hsg主要受辐射的影响, 晴天大于阴天的, 白天大于夜间的, 晴天最大值超过400 W·m-2, 阴天则为100 W·m-2左右, 夜间其值约为0 W·m-2. Hsw的日变化趋势主要受水面温度、环境空气温度和大气稳定度的影响.从日出到中午时段, 在太阳辐射的强迫下, 水面处于加热状态, 环境空气温度低于下垫面温度, Hsw为正通量, 蒸发皿水面释放能量.从中午开始, 随着太阳辐射的减弱和环境温度的不断增加, Hsw开始减小并在午后时分变为负值, 负Hsw一直持续到次日日出前.周围地表较大的感热能在平流作用下移到蒸发皿水面之上, 在湍流的作用下被水面吸收, 此时蒸发皿水面从环境吸收能量.日变化趋势分析表明, Hsw的量值约在正负100 W·m-2之间变动, 其大小与Hsg的强弱有关, 当Hsg较小时, Hsw为正值; 随着Hsg的增大, Hsw变为负值, 且Hsg越大, Hsw越小(即负通量越大), 这一现象揭示了在水面与周围地表所构成的非均匀条件下, 蒸发皿水面从周围环境获得平流感热能量的物理过程.
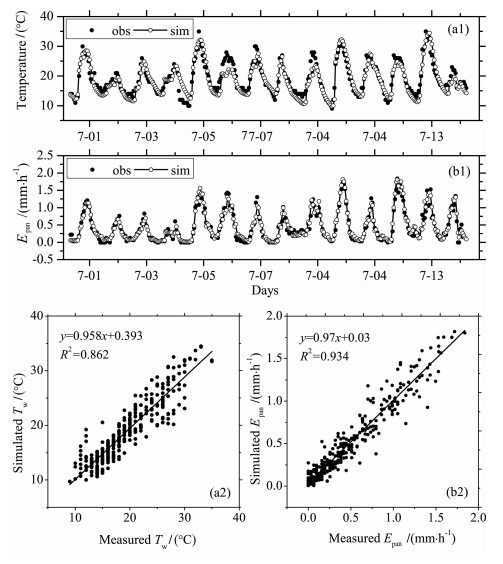
4.2 蒸发皿水温和蒸发量模拟蒸发皿水温高低影响蒸发皿蒸发强弱, 反过来蒸发强度又会影响水温的变化.水温变化反映了水体内能的变化, 是水体与周围环境之间各种形式的能量交换和转换的体现.利用以上建立的20cm蒸发皿蒸发模型对7月1-14日蒸发皿蒸发过程进行模拟, 图 4(a1)为蒸发皿水面温度模拟值与观测值的比较.结果显示, 除部分时段外(如4日夜间, 6日和9日中午时段), 模型能够较好地模拟蒸发皿水温日变化过程.水温模拟值与观测值回归分析结果显示(图 4(a2)), 模型基本能够再现蒸发皿水温的逐日变化和日变化趋势, 线性拟合斜率为0. 96, 截距为0. 40, R2为0. 86, 均方根误差(RMSE)为2. 24 ℃, 平均相对误差(MAER)为9. 2%.造成4日夜间, 6日和9日中午时段模拟误差过大的原因可能是由于蒸发皿底部热传导所致, 在特殊天气条件下, 底部发生较大的热通量, 但模型没有考虑底部热通量对水温的影响.另外, 水面反照率αw随太阳高度角有明显的日变化, 但为了简洁, 模型中αw设为常数, 这也可能是整个过程水温模拟误差较大的一个原因.
|
图 4 小时观测值与模拟值比较 (a1)、(a2)水温; (b1)、(b2)蒸发皿蒸发量. Fig. 4 Comparison the hourly measurements and simulation (a1)、(a2)Water temperature; (b1)、(b2)Pan evaporate rate. |
蒸发皿每小时蒸发量Epan(mm·h-1)模拟值与观测值的比较如图 4(b1)所示.观测结果显示, 受太阳辐射的影响, 晴天Epan明显大于阴天, 白天大于夜间的.典型晴天Epan在午后达到最大值2. 0mm·h-1; 在凌晨日出前, Epan几乎为零, 甚至在空气湿度较大的凌晨, 由于凝结现象, Epan还出现较小的负值. Epan模拟值与观测值回归分析结果显示(图 4(b2)), 模型能够很好地模拟Epan的日变化趋势, 观测值与模拟值的线性拟合斜率为0. 97, 截距为0. 03, R2为0. 93, 均方根误差(RMSE)为0. 013mm·h-1, 平均相对误差(MRER)为33. 8%.结果统计分析中导致MRER较大的原因是因为夜间Epan的量值很小, 从而在计算相对误差时因分母较小而导致MRER偏大.
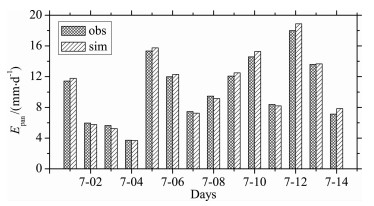
蒸发皿蒸发对气象因子的变化响应非常敏感, 天气尺度的气象因子变化对蒸发皿蒸发有明显的影响[16], 如晴天蒸发量明显大于阴天.为了检验该模型在不同天气条件下的模拟性能, 用蒸发皿日蒸发总量为标准对模拟结果进行评估.以当日01: 00时到24: 00时24时次Epan(mm·h-1)的和表示当日蒸发皿日蒸发量, 图 5为模型模拟的蒸发皿日蒸发量与观测值的比较.连续14天模拟的日蒸发量最大绝对误差为1. 3mm·d-1(7月12日), 最大相对误差为11. 8%(7月14日), 14天的均方根误差(RMSE)和平均相对误差(MRER)分别为0. 44mm·d-1和3. 7%, 日蒸发量观测值与模拟值的相关系数为0. 998, 这表明模型能够很好地反映不同天气条件对20cm蒸发皿蒸发的影响.
|
图 5 蒸发皿日蒸发量Epan(mm·d-1)模拟值和观测值比较 Fig. 5 Comparison the daily pan evaporation Epan (mm·d-1)by measured and simulated |
为了揭示蒸发皿蒸发的物理过程和能够定量分析各气象因子对蒸发皿蒸发的作用, 我们通过设置野外试验, 采用能量守恒和边界层理论, 借助陆面过程研究结果, 并考虑非均匀下垫面造成的局地能量平流和对边界层混合速度的影响, 构建了20cm蒸发皿的蒸发模型.本文的主要结论可归纳如下:
(1) 试验观测结果表明, 蒸发皿水面与周围地表构成显著的非均匀性, 在这种极端非均匀条件下, 蒸发皿蒸发潜热通量与地表净辐射的日总量平均比值为2. 66, 这表明蒸发皿蒸发所消耗的能量远大于周围环境净辐射能, 因此驱使蒸发皿蒸发的能量不仅仅为水面净辐射, 还包括来自周围较"热"下垫面上的能量输送.
(2) 以能量守恒原理和边界层梯度输送理论为基础, 考虑非均匀下垫面局地能量平流, 参数化蒸发皿侧壁发生的能量通量, 应用Monin-Obukhov相似理论计算蒸发皿水面感、潜热通量, 建立了一个单层的20cm蒸发皿蒸发模型.该模型有利于更好地研究蒸发皿蒸发量的物理意义, 为揭示蒸发皿观测量所代表的气候意义, 定量地分析各气象因子同蒸发皿蒸发量之间的关系提供数值依据.
(3) 模型模拟结果表明, 模型能够较好地模拟水面与周围地表之间的净辐射、感热通量所形成的非均匀差异; 同时也能模拟20cm蒸发皿的水温和蒸发的日变化过程; 连续14天蒸发皿日蒸发量模拟的均方根误差(RMSE)和平均相对误差(MRER)分别为0. 44mm·d-1和3. 7%, 日蒸发量观测值与模拟值的相关系数为0. 998.
本文所建立的20cm蒸发皿蒸发模型是以"古浪非均匀近地层观测试验"中所取得的观测资料为依据建立的, 该模型能否适用于其他季节或不同气候区20cm蒸发皿的蒸发模拟, 或者其他型号的蒸发皿(如E601B, ClassA), 甚至小水域的蒸发过程模拟, 还需要更多外场试验来验证和完善.
| [1] | Thom A S, Thony J L, Vauclin M. On the proper employment of evaporation pans and atmometers in estimating potential transpiration. QJR Meteorological Society , 1981, 107(453): 711-736. DOI:10.1002/qj.49710745316 |
| [2] | Stanhill G. Is the Class A evaporation pan still the most practical and accurate meteorological method for determining irrigation water requirements? Agric. For. Meteorol. , 2002, 112(3-4): 233-236. |
| [3] | Peterson T C, Golubev V S, Groisman P Y. Evaporation losing its strength. Nature , 1995, 377(6551): 687-688. |
| [4] | Roderick M L, Farquar G D. The cause of decreased pan evaporation over the past 50 years. Science , 2002, 298(5597): 1410-1411. |
| [5] | Brutsaert W, Parlange M B. Hydrological cycle explain the evaporation paradox. Nature , 1998, 396(5): 30-31. |
| [6] | Ji Y H, Zhuo G S. Important factors governing the incompatible trends of annual pan evaporation:evidence from a small scale region. Climatic Change , 2011, 106(2): 303-314. DOI:10.1007/s10584-010-9900-z |
| [7] | Rayner D P. Wind run changes:the dominant factor affecting pan evaporation trends in Australia. Journal of Climate , 2007, 20(14): 3379-3394. DOI:10.1175/JCLI4181.1 |
| [8] | Brutsaert W. Indications of increasing land surface evaporation during the second half of the 20th century. Geophys. Res. Lett. , 2006, 33(20): L20403. DOI:10.1029/2006GL027532 |
| [9] | Roderick M L, Farquar G D. Changes in Australian pan evaporation from 1970 to 2002. International Journal of Climatology , 2004, 24(9): 1077-1090. DOI:10.1002/(ISSN)1097-0088 |
| [10] | Zuo H C, Li D L, Hu Y Q, et al. Characteristics of climatic trends and correlation between pan-evaporation and environmental factors in the last 40 years over China. Chinese Science Bulletin , 2005, 50(12): 1235-1241. DOI:10.1007/BF03183699 |
| [11] | 左洪超, 鲍艳, 张存杰, 等. 蒸发皿蒸发量的物理意义、近40年变化趋势的分析和数值试验研究. 地球物理学报 , 2006, 49(3): 680–688. Zuo H C, Bao Y, Zhang C J, et al. An analytic and numerical study on the physical meaning of pan evaporation and its trend in recent 40 years. Chinese J. Geophys. (in Chinese) , 2006, 49(3): 680-688. |
| [12] | Monteith J L. Evaporation and the environment.//XIXth Symposia of the Society for Experimental Biology. University Press, Swansea, Cambridge, 1965:205-234. |
| [13] | Pereira A R, Villa Nova N A, Pereira A S, et al. A model for the Class A pan coefficient. Agriculture and Forest Meteorology , 1995, 76(2): 75-82. DOI:10.1016/0168-1923(94)02224-8 |
| [14] | Linacre E T. Estimating U. S. class-A pan evaporation from few climate data. Water Int. , 1994, 19(1): 5-14. |
| [15] | Roderick M L, Rotstayn L D, Farquhar G D, et al. On the attribution of changing pan evaporation. Geophysical Research Letters , 2007, 34(17): L17403. DOI:10.1029/2007GL031166 |
| [16] | Jacobs A F G, Heusinkveld B G, Lucassen D C. Temperature variation in a class A evaporation pan. Journal of Hydrology , 1998, 206(1-2): 75-83. DOI:10.1016/S0022-1694(98)00087-0 |
| [17] | Martinez J M M, Alvarez V M, González-Real M M, et al. A simulation model for predicting hourly pan evaporation from meteorological data. Journal of Hydrology , 2006, 318(1-4): 250-261. DOI:10.1016/j.jhydrol.2005.06.016 |
| [18] | Jacobs A F G, Hweusinkveld B G, Kraai A, et al. Diurnal temperature fluctuations in an artificial small shallow water body. Int. J. Biometerol. , 2008, 52(4): 271-280. DOI:10.1007/s00484-007-0121-8 |
| [19] | Chu C R, Li M H, Chen Y Y, et al. A wind tunnel experiment on the evaporation rate of Class A evaporation pan. Journal of Hydrology , 2010, 381(3-4): 221-224. DOI:10.1016/j.jhydrol.2009.11.044 |
| [20] | Mahrt L, Vickers D. Bulk formulation of the surface heat flux. Boundary-Layer Meteorology , 2004, 110(3): 357-379. DOI:10.1023/B:BOUN.0000007244.42320.1e |
| [21] | Gianniou S K, Antonopoulos V Z. Evaporation and energy budget in Lake Vegoritis, Greece. Journal of Hydrology , 2007, 345(3-4): 212-223. DOI:10.1016/j.jhydrol.2007.08.007 |
| [22] | 左洪超, 胡隐樵. 黑河试验区沙漠和戈壁的总体输送系数. 高原气象 , 1992, 11(4): 371–380. Zuo H C, Hu Y Q. The bulk transfer coefficient over desert and gobi in HEIHE region. Plateau Meteorology (in Chinese) , 1992, 11(4): 371-380. |
| [23] | Foken T. 50 years of the Monin-Obukhov similarity theory. Boundary-Layer Meteor. , 2006, 119(3): 431-447. DOI:10.1007/s10546-006-9048-6 |
| [24] | 戴永久, 曾庆存, 王斌. 一个简单的陆面过程模式. 大气科学 , 1997, 21(6): 705–716. Day Y J, Zeng Q C, Wang B. A simple land surface model for use in AGCM. Chin. J. Atmos. Sci. (in Chinese) , 1997, 21(6): 705-716. |
| [25] | 王丽娟, 左洪超, 陈继伟, 等. 遥感估算绿洲-沙漠下垫面地表温度及感热通量. 高原气象 , 2012, 31(3): 646–656. Wang L J, Zuo H C, Chen J W, et al. Land surface temperature and sensible heat flux estimated from remote sensing over oasis and desert. Plateau Meteorology (in Chinese) , 2012, 31(3): 646-656. |
 2013, Vol. 56
2013, Vol. 56