2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
大气运动中, 水平风除了有旋转和辐合辐散(气象上用涡度及散度分别度量其旋转及辐合辐散的强度)特性外, 水平风场还有一个显著的特性, 就是平流效应, 即水平风场自身的平流作用及其对各个物理量的水平输送, 如:温度平流、涡度平流、水汽平流等, 都被广泛用于天气系统发生发展的分析.周明煜等[1]对1998年夏季第2次青藏高原大气科学试验的观测资料的分析表明, 在对流层中平均风速垂直分布存在风切变现象, 水平平流作用对边界层结构有重要影响.在已往的研究结果中, 风场平流作用更多的是用于对涡度方程的分析, 如姚秀萍等[2]在研究热带对流层上空东风带影响西太平洋副热带高压活动时, 对垂直涡度方程进行了分析, 指出水平风场对涡度输送作用的贡献最大.周玉淑等[3]和Zhou等[4]则是考虑了风场平流效应的旋转, 推导得到了包含水平风平流旋转形式的涡度方程, 在2006年的bilis台风及2008年的Fung-Wong台风分析中得到了很好的应用, 但是该研究只讨论了水平平流旋转效应对涡度变化的贡献, 并没有考虑到平流的辐合辐散作用.杨平章等[5]在研究水平动量平流作用对热带气旋运动的影响时, 分析得到动量平流引起的水平动量辐合或辐散对台风路径异常变化有明显的影响.最近, 高守亭等[6]的研究提出加速度迁移项(反映水平风场平流的辐合辐散)能代表气块受到的所有力的散度, 即通过计算加速度迁移项就可以判断气块所受力的情况, 这为用加速度迁移项来研究大气运动提供了新的思路.由于加速度迁移项(也即是水平平流散度)与风场本身的分布一样, 是非均匀的, 且空间及时间变化很大, 也就是说, 水平平流的分布具有波动特征, 除了具有旋转效应外, 其辐合辐散效应也是一个重要方面.以往对水平平流作用及其旋转效应的研究还有一些结果, 但在其辐合辐散效应方面的研究尚属少见.而大气中的很多剧烈天气现象(尤其是中尺度灾害天气)往往是由风场及其水汽平流的不均匀产生的辐合辐散引起的.因此, 研究加速度散度迁移项(其反映了水平风场的平流作用)是中尺度天气研究中的一个重要内容.
根据二维亥姆霍兹定律, 水平风场可以分解为旋转风分量和辐散风分量, 引入风场的流函数和速度势后, 就可以直接用流函数和速度势分别表示风场的旋转和辐合辐散性质, 已在全球大气和大洋环流的诊断和数值模拟中有重要应用.依照这一思路, 本文对加速度迁移项也进行有旋和无旋分解, 可得到对应的加速度迁移项的流函数和位势, 利用加速度迁移项位势就可以反映出加速度迁移项的辐合辐散运动, 扩展了水平风场分解技术在中尺度天气研究中的应用.根据已有的研究, Chen和Kuo[7]提出的调和-余弦算法在有限区域风场分解和重建的精度最高, 而且物理意义也比其它方法明确, 在台风等低涡系统的风场分析中已有很好的应用[8-9].因此, 本文采用这一方法, 对加速度迁移项也进行调和-余弦的有旋和无旋分量的分解, 引入加速度迁移项位势概念, 以便利用加速度迁移项位势来研究东移高原低涡及台风系统演变过程.
2 加速度迁移项的调和-余弦分解方
法介绍水平加速度迁移项为(V· ΔV), 如用A表示加速度迁移项, 则可写为A=Axi+Ayj, 其两个分量的表达式为

|
(1) |
引入加速度迁移项的流函数及位势概念后, 有
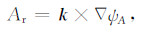
|
(2) |

|
(3) |
则加速度迁移项的流函数ψA及加速度迁移项位势χA与其旋转部分的垂直分量和散度分量之间有如下关系:

|
(4) |

|
(5) |
即:
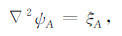
|
(6) |

|
(7) |
以上Ar和Ad为加速度迁移项的旋转分量和辐散分量, Δ ψA为加速度迁移项的流函数, Δ χA为加速度迁移项的位势, ξA和DA则分别是加速度迁移项的旋度的垂直分量和水平散度, 计算公式为

|
(8) |

|
(9) |
为得到有限区域泊松方程(6)和(7)的解, 在耦合边界条件下用调和-余弦算法[7]进行求解, 求解基本算法如下:
(1) 通过已有水平风分量u和v计算得到加速度迁移项的两个分量Ax和Ay后, 计算区域里的加速度迁移项项的涡度ξA和散度DA;
(2) 利用其次边界条件, 求解公式(10)所示的Possion方程, 该方程是公式(6)和(7)内部部分, 即:
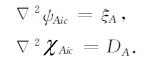
|
(10) |
通过傅里叶变换得到Possion方程(10)的解为

|
(11) |
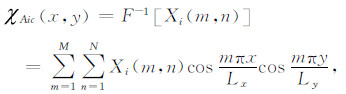
|
(12) |
其中, F-1是傅里叶逆变换算子, Φ和X是针对加速度迁移项的流函数和位势作了有限区域傅里叶余弦变换得到的双余弦展开式, 具体表达式为

|
(13) |
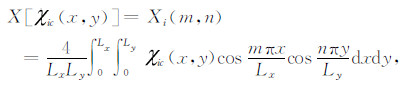
|
(14) |
其中下标i表示内部部分(inner part), 下标c表示余弦函数展开.
(3) 由计算出的ψAic和χAic, 利用二维亥姆霍兹原理得到加速度迁移项的内部分量AxIc和AyIc为

|
(15) |
(4) 计算加速度迁移项的外部分量AxEc和AyEc

|
(16) |
(5) 利用(4)得到的耦合边界条件:
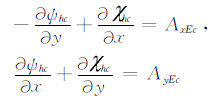
|
(17) |
来求解Laplace方程, 即在(17)的边条件下求解方程(18):
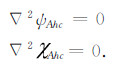
|
(18) |
其中, 下标h代表调和函数部分(harmonic part).
通过迭代求解(具体系数的计算参见文献[7]), 最终得到加速度迁移项的流函数和位势的调和分量为
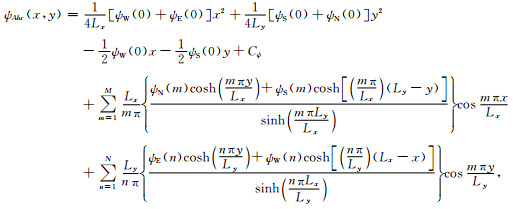
|
(19) |

|
(20) |
其中, ψW(0), ψW(n), …, ψE(0), ψW(n), …都是边界上的加速度迁移项的流函数和位势的谱系数, 下标E, S, W, N分别表示东、南、西、北四个方位.
(6)由方程(11)、(12)和(19)、(20), 得到计算的有限区域的加速度迁移项的流函数和位势分量为
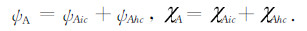
|
(21) |
这样求解得到的物理量具有很明确的物理意义:加速度迁移项的流函数和位势的内部分量ψAic和χAic完全由有限区域内部的加速度迁移项的旋转垂直分量及其散度决定, 边界条件都是齐次的, 所以边条件对内部分量没有影响; 而调和分量ψAhc和χAhc是通过求解Laplace方程得到的, 完全由区域的边界条件决定, 因而极值只出现在边界上.在这样的求解过程中, 只需要通过极少的迭代次数就能达到很好的收敛效果, 计算效率和精度都大大提高.
由于本文关心的主要是加速度迁移项的辐合辐散作用对天气系统的影响, 以下的分析就用加速度迁移项位势部分, 即χA的分布来讨论其在具体天气系统演变中的示踪作用.
3 加速度迁移项位势在低涡及台风系统分析中的应用由于平流的作用在大气运动中无处无时不在, 其辐合辐散作用必然会对系统演变有所指示.由于低涡及台风系统都是具有明显的平流旋转和辐合的系统, 本节就以一个东移高原低涡及登陆我国的Bilis台风(2006年第4号台风)系统为例, 分析高原低涡东移及台风系统演变过程中加速度迁移项位势的变化, 以期为示踪及反应低涡及台风系统的演变提供一个新的物理变量.
3.1 在东移高原低涡中的应用高原低涡是引发高原地区暴雨天气的重要系统之一, 在适当的环流条件配合下可以向东移出高原, 并在适当条件下发展, 往往会造成周边及下游地区(如江淮流域等)出现暴雨等灾害性天气[10-12].基于高原低涡研究的需要, 本节首先将加速度迁移项位势用于2008-07-20-08: 00到21日14: 00的一次青藏高原低涡东移的个例分析中[13], 所用资料为NCEP/NCAR的分析资料, 空间分辨率为110km, 时间分辨率为6h.首先分析这次高原低涡东移出高原的天气过程.
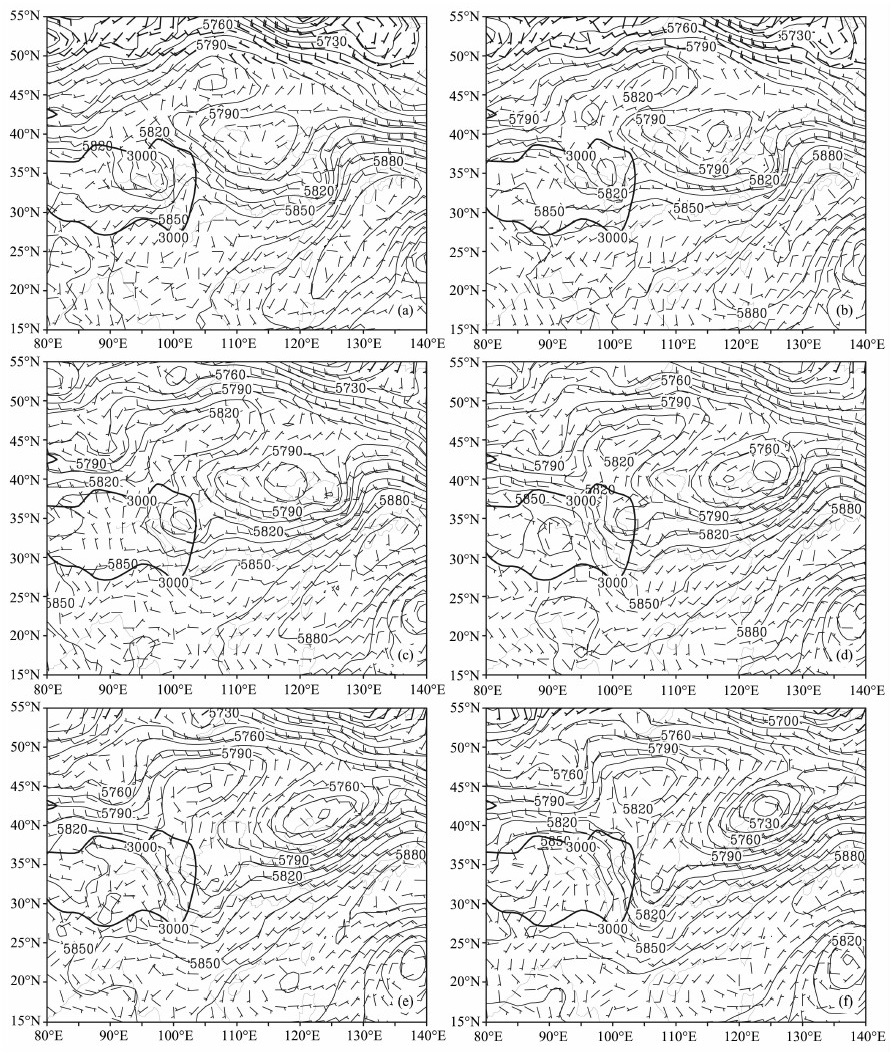
在500hPa天气图上, 图 1a中中高纬度影响中国的主要槽脊系统是青藏高原北部的低压槽(简称西部槽)和贝加尔湖以南的高压脊(简称东部脊), 其中西部槽比较深厚, 而东部脊相对范围比较小, 且东部脊的东南部河套平原附近存在一个闭合的低压中心.在40°N以南, 高原东部附近(97°E, 35°N)上空存在一个明显的闭合低压中心, 即为本节分析的高原低涡.黄海上空也存在一个小的闭合低压系统. 6小时后(20日14: 00, 图 1b), 中高纬地区槽脊系统东移, 东部脊进一步加强, 高压脊东南部河套附近低压中心东移加强, 位势高度最小值降至5775位势米.此时青藏高原东部高原涡东移至(98°E, 35°N)附近, 5805等高线所围面积减小. 20日20: 00(图 1c), 河套附近低压中心进一步东移加强, 5775等高线范围扩大, 而高原低涡东移至高原东边缘附近, 强度变化不大, 此时高原涡位于河套低压西南边缘.至21日02: 00(图 1d), 河套低压东移至朝鲜半岛, 强度进一步加强, 等高线最小值达5745位势米, 此时高原涡不再有闭合等高线, 而是并入东移的河套低压区, 以小槽形式存在, 同时高原东侧边缘的低槽较前一时刻向南发展, 5850位势米等值线南伸到23°N. 21日08: 00(图 1e), 原河套低压继续增强向东移动, 高原东侧低槽也进一步加深东移, 且槽线由横槽逐渐转为竖槽, 位置在105°E附近.到21日14: 00 (图 1f), 高原东侧低槽强度加强, 移出高原后向东北方向移动.
|
图 1 500 hPa位势高度场(单位:位势米)和风场(单位: m/s)分布 (a)2008-07-20-08: 00; (b)2008-07-20-14: 00; (c)2008-07-20-20: 00; (d)2008-07-21-02: 00; (e)2008-07-21-08: 00; (f)2008-07-21-14: 00. |
从公式(7)可知, 用余弦谱展开后, 加速度迁移项位势的拉普拉斯符号与平流本身的符号相反, 也就是说, 当加速度迁移项位势为正时, 其散度为负, 表示加速度迁移项是辐合的.从加速度迁移项位势的分布来看, 对2008年7月20日08: 00, 500hPa上的高原东部, 也是在(97°E, 35°N)附近有明显的加速度迁移项位势的正值区(图 2a), 与位势高度分析显示的高原低涡的位置相当, 表示低涡处有明显的加速度迁移项的辐合.从加速度迁移项位势的正值区及其中心分布来看, 它比500hPa位势高度表示的低涡系统更为清楚.而且, 黄海上空的闭合低压系统及槽区, 也有明显的加速度迁移项位势的正值中心及正值区对应, 这说明用加速度迁移项位势确实可以示踪和识别低涡系统. 6小时后, 高原低涡东移到(100°E, 35°N)附近(图 1b), 对应时刻的加速度迁移项位势的正值区及正值中心也东移到同样的位置(图 2b), 说明低涡系统中确实一直存在加速度迁移项的辐合作用, 也正是由于水平风的加速度迁移项的辐合, 低涡才能得以维持和发展.到7月20日20: 00和21日02: 00, 低涡移到高原东部斜坡地形附近, 虽然风场上还存在气旋性环流, 但在位势高度分布上已经没有闭合的等压线, 而是一个槽区(图 1c和图 1d), 但在同时刻的加速度迁移项位势分布上(图 2c和图 2d), 在低槽区位置, 仍然有明显的加速度迁移项位势正值区和正值中心, 对指示东移高原低涡的位置比位势高度更为清晰.随着低涡并入低槽并移出高原后, 槽区范围加强南伸并继续东移, 对应的加速度迁移项位势分布图上(图 2e和图 2f)也有加速度迁移项位势范围的扩展和加强, 与位势高度反映的趋势是一致的, 说明用加速度迁移项位势确实可以示踪高原低涡的东移演变过程.

|
图 2 500 hPa加速度迁移项位势(单位: m2·s-2)分布 (a)2008-07-20-08: 00; (b)2008-07-20-14时; (c)2008-07-20-20: 00; (d)2008-07-21日02: 00; (e)2008-07-21日08: 00; (f)2008-07-21-14: 00. |
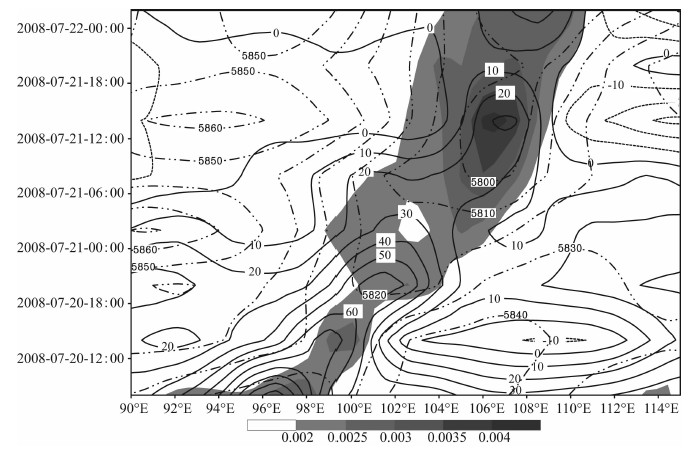
图 3是500hPa面上位势高度与加速度迁移项位势及位涡在30°N-35°N之间平均的经度-时间演变图, 从图中可见, 从7月20日08: 00开始, 随着低涡从高原中东部开始东移直至移出高原的过程中, 实线表示的加速度迁移项位势从高原到下游地区随时间呈现出一条明显的正值中心区, 与阴影区表示的位涡的正异常区域是一致的, 说明加速度迁移项位势确实可以用以示踪低涡的东移演变.不同的是, 加速度迁移项位势表示的辐合运动在高原上时较强, 而位势高度及位涡则是随后加强的, 在时间上稍微滞后于加速度迁移项位势的加强.当低涡东移出高原并入低槽中加强后, 加速度迁移项位势是减弱的, 此时位势高度减小, 位涡正异常也加大, 表明低槽加深加强.可以推测, 这个低槽加强可能与前期加速度迁移项位势的辐合有关, 这与天气学上用风场辐合可导致低涡加强的动力过程的描述也是一致的, 也进一步说明加速度迁移项位势所指示的辐合辐散对系统的强度变化有一定的动力指示意义.
|
图 3 500 hPa加速度迁移项位势(实线, 单位: m2·s-2), 位势高度(点点虚线, 单位: gpm)及位涡(阴影区表示PV大于0.2的区域, 单位: PVU)的经度-时间剖面 |
从以上对东移高原低涡的分析可见, 由于加速度迁移项位势包含了水平风场平流的辐合辐散动力特征, 因此, 从加速度迁移项位势的分布, 我们就可以直接判断低涡系统的水平风场平流的辐合辐散动力效应, 而不用再分析其散度的分布.而且, 随着空间分辨率越来越高, 计算的散度分布会越来越乱, 而加速度迁移项位势的分布相对于散度分布来说要光滑很多.因此, 作为一个新的动力变量, 加速度迁移项位势的引入可用于示踪东移高原低涡系统以及指示低涡系统的平流的辐合辐散效应.
以上是加速度迁移项位势在东移高原低涡系统分析中的应用, 以下分析其在登陆台风中的应用.
3.2 在登陆台风Bilis中的应用登陆台风是造成我国暴雨的又一个主要系统, 2006年的4号台风Bilis在整个发展过程中, 结构松散, 中心附近对流不强, 没有眼壁和风眼结构, 没有统一的台风中心, 风力不是特别强, 但含水量大, 造成南方地区大面积洪涝, 以及山体滑坡和泥石流等次生灾害, 是近十年来台风灾害导致伤亡人数最多的一次, 本小节以Bilis为例进行加速度迁移项位势的分析.所用资料为日本气象厅区域谱模式(RSM)再分析资料, 空间分辨率为20km, 时间分辨率为6h.
从图 4可见, 无论是Bilis台风登陆前(图 4a, b, c)还是登陆后(图 4d), 与位势高度类似(图略), 实线所示的加速度迁移项位势都能较好地指示出台风系统, 加速度迁移项位势的正值中心与台风中心位置比较接近, 用加速度迁移项位势的正异常中心可以大概判断出台风中心位置.此外, 从加速度迁移项位势与水平风散度的分布来看, 加速度迁移项位势等值线相对密集的区域, 也就是加速度迁移项位势梯度较大的区域, 往往也是散度较大的区域(这个特征在图 4c中表现最显著, 环状深色阴影区代表的辐合区与加速度迁移项位势等值线分布较密集的区域基本是一致的).在加速度迁移项等值线曲率变化大的地方(这种区域加速度迁移项位势的拉普拉斯算子最大), 一般也对应着散度大值区, 如图 4a中, 在Bilis的东南部(122°E, 21°N)附近, 加速度迁移项位势的400和600的等值线有明显的弯曲, 对应着明显的辐合发生(图中阴影区); 图 4b中, 台风西侧的加速度迁移项位势有小范围弯曲的地方, 也是辐合较强的区域; 又如图 4c中, 在台风中心南侧, 从外到内都有加速度迁移项位势等值线发生明显弯曲, 也对应着无旋风的辐合大值区及散度大值区.在图 4d中, 由于台风登陆后, 受复杂下垫面条件影响, 台风结构不再像洋面上时那样规则, 但是也可分析得到加速度迁移项位势的等值线曲率大的区域, 也基本对应着较强的辐合运动. 图 4中阴影区只表示了辐合发生的区域, 如果全标出辐合辐散运动会发现, 整个散度场的分布比较凌乱, 对分析台风动力结构并不清楚.但是从加速度迁移项位势分布看, 只要注意加速度迁移项位势正值中心区及其等值线曲率变化较大的区域, 就基本可以判断出大的辐合区域.从加速度迁移项位势的数值看, 在洋面上时, 其数值较大, 中心等值线为1400, 最强时达到1600(图略), 随着台风的移动及登陆, 数值从1600逐渐降低到300多, 其数值演变趋势与台风强度的变化也是一致的.因此, 加速度迁移项位势的强弱也可表示出台风系统的强度变化.

|
图 4 850 hPa上加速度迁移项位势(实线, 单位: m2·s-2), 无旋风(矢量, 单位: m·s)及散度(阴影区, 单位: 1×10-4·s-1)分布(a)2006-07-12-20: 00; (b)2006-07-13-08: 00; (c)2006-07-14-02: 00; (d)2006-07-14-20: 00.图中粗虚线为Bilis台风路径, 台风符号表示当前时刻台风中心位置. |
从本节加速度迁移项位势对Bilis台风的分析可见, 它可指示台风系统位置及辐合大值区的位置以及台风强度的演变趋势.可见, 加速度迁移项位势可用于指示台风系统以及显示台风系统里的辐合辐散运动特征, 还可反映台风系统强度, 可作为一个新的动力诊断变量来示踪台风的强度变化及其辐合辐散效应.
4 结论在高守亭等[6]对加速度迁移项散度作用研究的基础上, 即:加速度迁移项能代表气块受到的所有力的辐合或辐散效应, 通过计算加速度迁移散度项就可以判断气块受到的力的辐合或辐散情况, 本文对加速度迁移项进一步进行调和-余弦的分解, 并引入加速度迁移项位势的概念, 用加速度迁移项对应的位势部分(可反映平流的辐合辐散)对东移高原低涡及登陆台风Bilis的演变过程进行了分析.结果表明加速度迁移项位势对低涡系统有较好的描述作用, 用于指示东移的高原低涡系统较常用的500hPa位势高度场对低涡的分析更为清晰.此外, 加速度迁移项位势用于登陆台风Bilis的分析也表明, 它可指示台风环流系统, 还可用以判断洋面上台风的中心位置以及台风强度变化.由于加速度迁移项位势可反映出水平平流的辐合辐散, 可以作为一个新的动力变量来诊断并示踪低涡及台风等天气系统的演变.
| [1] | 周明煜, 钱粉兰, 陈陟, 等. 西藏高原斜压对流边界层风、温、湿廓线特征. 地球物理学报 , 2002, 45(6): 773–783. Zhou M Y, Qian F L, Chen Z, et al. The characteristics of the profiles for wind, temperature and humidity in the baroclinic convective boundary layer on Xizang plateau. Chinese J. Geophys. (in Chinese) , 2002, 45(6): 773-783. |
| [2] | 姚秀萍, 吴国雄, 刘屹岷, 等. 热带对流层上空东风带扰动影响西太平洋副热带高压的个例分析. 气象学报 , 2007, 65(2): 198–207. Yao X P, Wu G X, Liu Y M, et al. Case study on the impact of the vortex in the easterlies over the tropical upper troposphere on the subtropical anticyclone over western Pacific Ocean. Acta Meteorologica Sinica (in Chinese) , 2007, 65(2): 198-207. |
| [3] | Zhao Y S, Liu L P. Analyses of wind structure of typhoon fung-wong (2008) and its relation to precipitation region. Journal of Tropical Meteorology , 2009, 15(2): 192-203. |
| [4] | 周玉淑, 冉令坤. 平流涡度方程及其在2006年Bilis台风分析中的应用. 物理学报 , 2010, 59(2): 1367–1377. Zhou Y S, Ran L K. Advective vorticity equation and its application to the vorticity variation of typhoon Bills in 2006. Acta Physica Sinica (in Chinese) , 2010, 59(2): 1367-1377. |
| [5] | 杨平章, 贺海晏. 非线性水平动量平流作用对热带气旋运动的影响. 中山大学学报(自然科学版) , 1995, 34(1): 82–89. Yang P Z, He H Y. The effect of non-linear horizontal momentum advection on tropical cyclone motion. Acta Scientiarum Naturalium Universitatis Sunyatseni (in Chinese) , 1995, 34(1): 82-89. |
| [6] | 高守亭, 邓涤菲, 周玉淑. 加速度迁移项散度在涡旋系统动力识别上的初步应用. 地球物理学报 , 2011, 54(4): 875–885. Gao S T, Deng D F, Zhou Y S. The effect of the divergence of relocation term in acceleration and its application to the dynamic identification of vortex system. Chinese J. Geophys. (in Chinese) , 2011, 54(4): 875-885. |
| [7] | Chen Q S, Kuo Y H. A consistency condition for wind-field reconstruction in a limited area and a harmonic-cosine series expansion. Mon. Wea. Rev. , 1992, 120(11): 2653-2670. DOI:10.1175/1520-0493(1992)120<2653:ACCFWF>2.0.CO;2 |
| [8] | 周玉淑, 曹洁, 高守亭. 有限区域风场分解方法及其在台风SAOMEI研究中的应用. 物理学报 , 2008, 57(10): 6654–6665. Zhao Y S, Cao J, Gao S T. The method of decomposing wind field in a limited area and its application to typhoon SAOMEI. Acta Physica Sinica (in Chinese) , 2008, 57(10): 6654-6665. |
| [9] | 周玉淑, 曹洁. 有限区域风场的分解和重建. 物理学报 , 2010, 59(4): 2898–2906. Zhou Y S, Cao J. Partitioning and reconstruction problem of the wind in a limited region. Acta Physica Sinica (in Chinese) , 2010, 59(4): 2898-2906. |
| [10] | 高文良, 郁淑华. 高原低涡东移出高原的平均环流场分析. 高原气象 , 2007, 26(1): 206–212. Gao W L, Yu S H. Analyses on mean circulation field of the plateau low vortex moving out of Tibetan Plateau. Plateau Meteorology (in Chinese) , 2007, 26(1): 206-212. |
| [11] | 郁淑华, 高文良. 高原低涡移出高原的观测事实分析. 气象学报 , 2006, 64(3): 392–399. Yu S H, Gao W L. Observational analysis on the movement of vortices before/after moving out the Tibetan Plateau. Acta Meteorologica Sinica (in Chinese) , 2006, 64(3): 392-399. |
| [12] | 郁淑华, 高文良. 青藏高原低涡移出高原的大尺度条件. 高原气象 , 2008, 27(6): 1276–1287. Yu S H, Gao W L. The Large-Scale conditions of the vortex moving out of Qinghai-Xizang plateau. Plateau Meteorology (in Chinese) , 2008, 27(6): 1276-1287. |
| [13] | 何光碧, 高文良, 屠妮妮. 两次高原低涡东移特征及发展机制动力诊断. 气象学报 , 2009, 67(4): 599–612. He G B, Gao W L, Tu N N. The dynamic diagnosis on easterwards moving characteristics and developing mechanism of two Tibetan Plateau vortex processes. Acta Meteorologica Sinica (in Chinese) , 2009, 67(4): 599-612. |
 2013, Vol. 56
2013, Vol. 56

